混合局部因果結構學習

王雲霞，曹付元+，凌兆龍

1.山西大學計算機與信息技術學院，太原 030006

2.山西大學計算智能與中文信息處理教育部重點實驗室，太原 030006

3.安徽大學計算機科學與技術學院，合肥 230601

因果關系發現在計算機科學領域發揮著重要的作用，比如面向多源數據的因果關系發現[1-3]，選擇與類別屬性有因果關系的特征來增強機器學習模型的泛化能力與可解釋性[4]，利用因果理論解決復雜的機器學習問題[5-6]等。因果結構學習是識別變量之間因果關系的一個學習過程，而挖掘一個與數據擬合程度較好且包含所有變量的全局（或完整）的貝葉斯網絡可以學習變量之間的因果關系[7-8]。但是大數據時代的到來使得越來越豐富的數據為因果結構學習帶來更多信息的同時也帶來了相應的挑戰。一方面豐富的數據含有更多的信息，為因果結構學習提供了更多的數據支撐，另一方面數據的維度越來越高，其在計算時間和空間存儲上消耗較大，全局因果結構學習將變得困難甚至在更大型的數據集上無法運行。此外，如果僅僅對高維數據中某一部分變量之間的因果關系感興趣時，構建全局網絡是浪費時間與空間的。因此相對于全局因果結構學習方法，局部因果結構學習方法可以在高維數據中挖掘任意感興趣變量的局部因果結構，且從計算資源與存儲資源的角度，局部因果結構挖掘更高效且更具有實際意義。

Silverstein 等人提出第一個局部因果結構學習算法，即LCD（local causal discovery）算法[9]，該算法利用條件獨立性學習四個變量之間的因果關系。基于LCD 算法，Mani 等人提出BLCD（Bayesian local causal discovery）算法[10]，它首先學習目標變量的馬爾科夫毯（Markov blanket，MB），然后學習MB 中的Y 結構來進行局部因果結構的學習。但是上述的兩個算法并沒有識別到目標變量的直接原因和直接結果。基于LCD 算法和BLCD 算法的不足，Yin 等人提出了PCD-by-PCD（parents，children and some descendants）算法[11]，該算法首先利用MMPC（max-min parents and children）算法[12]學習目標變量的PC 集，然后利用條件獨立性測試尋找其中的V 結構，遞歸地推出PC集中變量之間的因果關系。Gao等人提出CMB（causal Markov blanket）算法[13]，其基本思想與PCD-by-PCD算法一致，該算法首先調用HTION-MB 算法[14]尋找目標變量的MB，然后利用條件獨立性測試和Meek規則遞歸地推導邊的方向。但是上述兩個算法的精度相對不是很高，且有限樣本下其精度更差。其原因是一方面受到PC（parents and children）發現結果的影響，另一方面是邊的定向過程中對V 結構的依賴性也會使得算法精度不穩定。

目前已有的局部因果結構學習算法分為兩個步驟：步驟1 是發現目標變量的MB 或PC，即目標變量的局部結構骨架[15-16]；步驟2 是對PC 集中的變量確定其與目標變量之間的因果關系。兩個步驟的結果都對最終的算法產生一定的影響。

步驟1 中PCD-by-PCD 算法和CMB 算法分別調用基于限制的因果關系發現算法：MMPC 算法和HTION-MB 算法來發現目標變量的局部結構骨架。而這兩個算法都是直接利用條件獨立性學習MB/PC，其對數據樣本大小有一定的要求，當數據樣本沒有達到MB/PC 尺寸的指數級數量時，算法所用的條件獨立性測試將有較高的錯誤率，進而導致這兩個方法的精度較差。為了解決上述問題，本文在基于限制方法的基礎上結合打分方法來緩減有限樣本問題，原因是打分方法具有更強的容錯性，能夠通過搜索一個明顯較小的空間收斂到一個更高質量的網絡，且基于分數的方法在可能的圖結構中有更強的先驗性，可以緩減影響算法精度的有限樣本問題。而單純的采用打分的方法如S2TMB（score-based simultaneous Markov blanket）算法[17]，由于其是對每一個變量逐一考慮進行打分，時間效率極低。因此本文結合兩種思想來綜合提高步驟1 性能。

步驟2 中PCD-by-PCD 算法和CMB 算法都是直接利用條件獨立性測試尋找V 結構，然后利用Meek規則確定邊的方向來得到目標變量的局部結構。一方面因為V 結構依賴于基本網絡結構，而算法結果又依賴于V 結構的發現即當正確發現的V 結構很多且與目標變量有關系時，最終算法的精度相應較高，當正確發現的V 結構很少且與目標變量沒有關系時，那么最終算法的精度將會大幅度降低。因此這兩個算法最終得到的結果精度是要依賴于基本網絡中V 結構的發現[18]。另一方面同樣由于有限樣本等影響，條件獨立性測試將存在一定的錯誤性，這也就意味著V結構發現以及Meek 規則的使用將存在一定的錯誤性，從而導致最終算法精度相對不高。因此為了降低對V 結構的依賴性且緩減有限樣本問題，同時提高相對于打分方法的時間效率，本文結合限制與打分方法對已有的局部因果結構學習算法進行改進來提高算法的精度。

本文提出一種新的基于打分和限制相結合的混合局部因果結構學習算法（hybrid local causal structure learning，HLCS）。步驟1 對基于打分的PC 發現算法進行了改進，通過加入限制思想降低所測試的節點數目，且輸出目標變量與其PC 集變量的定向結果，提出一種基于打分和限制相結合的PC 發現算法SIAPC（score-based incremental association parents and children）；步驟2 通過利用SIAPC 算法得到的定向結果和對部分數據集打分得到的定向結果的交集來確定邊的方向，之后結合條件獨立測試來降低對V 結構的依賴性。實驗結果驗證了本文方法相對于目前的方法在精度方面有顯著提高，且有效緩減了數據效率問題。

1 背景知識

為方便可讀，本文用V=(X1,X2,…,Xn)表示n個觀測變量（節點），P是V上的一個離散的聯合概率分布，G代表一個有向無環圖DAG 。如果滿足馬爾科夫條件，則稱為一個貝葉斯網絡。在一個貝葉斯網絡中，Xi⊥Xj和分別表示變量Xi、Xj之間的獨立性和依賴性，Xi⊥Xj|Z表示在集合Z的條件下，變量Xi條件獨立于Xj，其中Z?V{Xi,Xj}，同理表示在Z的條件下，變量Xi條件依賴于Xj。下面給出一些相關的定義。

定義1（馬爾科夫條件）[19]給定一個有向無環圖G，馬爾科夫條件在G中成立當且僅當G中的每一個節點都獨立于它的非后裔節點的任何子集。

馬爾科夫條件使得貝葉斯網絡對一組變量V的聯合概率實現分解化，即P(V)可以分解為G中在給定父集條件下變量條件概率分布的乘積，其中PA(T)是G中變量X的父集，則P(V)被表示為：

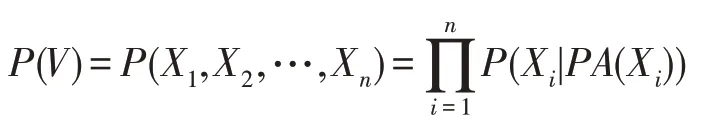
定義2（條件獨立性）[19]兩個不同的變量Xi,Xj∈V被認為在給定變量子集Z?V{Xi,Xj}下是條件獨立的當且僅當P(Xi,Xj|Z)=P(Xi|Z)P(Xj|Z)成立，否則Xi、Xj被認為在變量子集Z下條件依賴。

定義3（d-分離）[20]在一個有向無環圖G中，一條路徑π被集合Z?Vd-分離當且僅當（1）π中包含Xi→Xk→Xj（Xi←Xk←Xj）或Xi←Xk→Xj，其中中間節點Xk屬于Z即Xk∈Z，或（2）π中包含一個V 結構Xi→Xk←Xj，此時中間節點Xk不屬于Z，且Xk的子孫節點也不在Z中。集合Z被認為d-分離Xi，Xj當且僅當Z阻隔了從Xi到Xj的每條路徑。

定義4（忠實性假設）[21]給定一個貝葉斯網絡，G忠實于P當且僅當P中的每個條件獨立都受G和馬爾科夫條件的影響。P是忠實的當且僅當G對P忠實。

定義5（馬爾科夫毯）[21]忠實性假設下，在一個貝葉斯網絡中，一個變量T的馬爾科夫毯MB(T)是唯一的且包含其父母PA(T)、孩子CH(T)和配偶SP(T)（變量的孩子的其他父母），即MB(T)=PA(T)?CH(T)?SP(T)。

定義6（近似PC 集）在一個貝葉斯網絡中，設CSet(T)為與變量T相關的節點集且Xi,T∈V），若T⊥Xi|Xk且Xi∈CSet(T),Xk∈CSet(T){T,Xi}，則從CSet(T)中去掉Xi，最終剩下的節點集定義為目標變量T的近似PC 集，記作SPC(T)。

定義7（環繞結構）給定一個貝葉斯網絡，忠實性假設下，若存在三個以上的節點構成的結構滿足以下條件：（1）節點數目等于邊的數目；（2）該結構的每一節點都有兩條邊相連；（3）Xi⊥Xj|Z且，Z?V{Xi,Xj}，則稱該結構為環繞結構。

2 基于打分和限制相結合的混合局部因果結構學習算法

局部因果結構學習方法通常包括兩個步驟：（1）挖掘目標變量的MB/PC；（2）迭代進行邊的定向，得到目標變量的局部結構。圖1 展示了一個因果網絡結構，假設目標變量為T，則由圖1 可知T的PC 集為PC(T)={N,A,L,J,B,C}，而{T,A,D,L}和{T,B,F,M,C}構成的結構是定義7 的環繞結構。

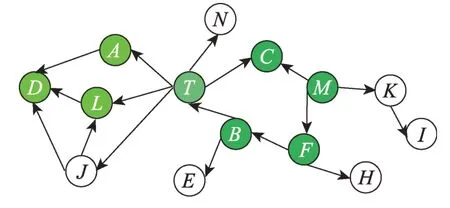
Fig.1 Causal network structure 1圖1 因果網絡結構1

理論上基于限制的方法可以得到正確的PC/MB，但是有限樣本問題導致的條件獨立性測試存在一定的錯誤性，因此最終得到的目標變量的PC/MB 可能不是完全正確的。而基于打分的學習方法使用帶分數標準的BN（Bayesian network）結構學習算法來查找局部結構，其在可能的圖形結構上具有更強的先驗性，且打分方法MMHC（max-min hill-climbing）在有限樣本中可以收斂到一個更高質量的網絡。因此為了解決由有限樣本產生的條件獨立性導致的錯誤以及由打分方法本身產生的時間效率問題，本文結合基于限制和基于打分-搜索的方法，綜合考慮PC/MB 發現，提出SIAPC 算法。

以圖1 為例，由于馬爾科夫等價類的存在，已有的局部因果結構學習算法在結構{T,C,F,M,B}中，無法確定T和{B,F,M}之間的關系；同理在結構{T,A,D,L}中，也無法確定T和{A,L}之間的關系。因此已有的局部因果結構學習算法在面對上述結構中，需要尋找更多的V 結構來判斷邊的方向，但是V 結構依賴于基本網絡結構，因此算法最終得到的結果精度要取決于V 結構的發現。而打分方法因為在可能的圖形結構上具有更強的先驗性，其可以降低算法對V結構的依賴性，所以為了解決已有算法對V 結構依賴問題，緩減數據效率問題，本文結合打分方法對基于限制的局部因果結構學習算法進行改進，提出混合的局部因果結構學習算法HLCS。

2.1 挖掘目標變量的PC 集

設與變量X依賴的集合為CSet(X)，與變量X獨立的集合為CC(X)，由于變量X的PC 集PC(X)是與X直接相連的節點集，因此PC(X)是CSet(X)的子集，即PC(X)?CSet(X)。由定義3，在CSet(X)中發現存在集合S可以阻斷X和Y（Y∈CSet(X){S,X}）之間的路徑，則Y一定不屬于PC(X)，也就是可以被阻斷的節點不是和X直接相連的節點，因此可以對Y∈CSet(X)與X之間的路徑用d-分離進行測試，得到變量X的最終的PC 集PC(X)。

在圖2 中，設藍色節點為目標節點T，綠色節點表示PC(T)={A,B,C,L}，經分析綠色節點和黃色節點構成CSet(T)={A,B,C,L,D,E,F,H}，此時對于目標節點T來說，D被{A,L}阻斷，E被B阻斷，H被F阻斷，F被B阻斷，因此CSet(T)中剩下的節點為{A,B,C,L}，即最終變量T的PC 集為PC(T)={A,B,C,L}。

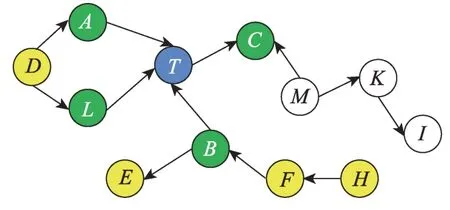
Fig.2 Causal network structure 2圖2 因果網絡結構2

但是上述思想存在以下問題：（1）非常依賴條件獨立測試的正確性且僅僅關注CSet中的變量的情況；（2）當近似PC 集的長度很大時，所需要的條件獨立測試次數將呈指數級增長，即設ns=|SPC|。由于條件集長度為1 時CSet可以去掉大部分在其中的節點，之后對剩下的節點集也就是近似PC 集考慮條件集長度為i=2,3,…,ns，此時相對于CSet的長度僅僅去掉少部分節點，因此本文計算條件獨立測試的次數，直接使用ns作為近似測試次數，即近似結果為：

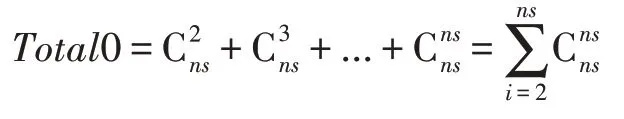
經分析，上述思想總的獨立性測試次數為Total=|V|+|CSet|2+Total0，但是這種方法的條件獨立性測試次數相對較多，最終的結果精度不是很高。為了進一步減少條件獨立測試次數，本文直接將Xi∈CSet(T)作為條件集測試Xj∈CSet(T)和T之間的獨立性，進而得到T的近似PC 集SPC(T)。此方式可以使條件獨立測試次數減少到Total=|V|+|CSet|2，且最終保留較少節點在SPC(T)中（PC(T)?SPC(T)）。同時為了緩減對條件獨立測試正確性的依賴，本文采用已有基于打分-搜索的方法對CC(T)與SPC(T)中的變量共同考慮，來尋找最終的PC(T)。對{CC(T),SPC(T)}共同考慮的原因是：（1）目標節點T與X∈SPC(T) 和Y∈CC(T)可能會構成V 結構。如圖2 所示，C是T的PC 節點，且＜T,C,M＞構成V 結構，可以進一步確定C是T的PC 節點。（2）由于SPC(T)是對CSet(T)的精簡，每次對數據集DATA{T,X,PC(T)},X∈{SPC(T),CC(T)}進行打分，得到的PC(T)的長度都較小，這使得算法效率更高。本文采用基于打分-搜索的全局因果結構學習算法MMHC 進行打分判定，且其使用的分數準則為BDeu。

基于上述分析，本文提出以下改進的PC 發現算法SIAPC，如算法1。

算法1SIAPC

輸入：數據集DATA，目標變量T，獨立性指標w0。

輸出：PC為T的PC集，CSet為與T依賴的集合，SPC為T的近似PC 集，PA為T的父集，CH為T的子集。

2.2 迭代進行邊的定向

由于上述的PC 發現算法用打分方法只能確定和目標變量T相連的一部分邊的方向，且由于是對一部分數據集進行打分，最終得到錯誤的邊定向結果是相對較多的，由此在邊的迭代定向過程中要進行邊方向的進一步確定與修正；在迭代邊定向過程中用到的原則就是尋找V 結構，如圖3 中的＜A1,T1,B1 ＞，＜A2,T2,B2 ＞構成V 結構，但A1、B1 存在依賴關系，A2、B2 存在依賴關系，即＜Ai,Ti,Bi＞構成V結構，Ai、Bi之間存在依賴關系（i=1,2,…,n）。此時可以檢測＜Ai,Ti,Bi＞為V 結構，但是對于V 結構之外的路徑判斷不了邊的方向。面對上述結構，已有的基于限制的方法會進一步尋找更多的MB 或PC集去確定更多的V 結構，算法結果依賴于發現的V 結構且在大部分網絡中性能較低。

Fig.3 Two examples of surround structure圖3 環繞結構的兩種示例

基于上述問題本文結合打分方法進行改進。由于基于打分-搜索的方法在可能的圖形結構上具有更強的先驗性，其在實踐中表現相對比較穩定，尤其是在樣本量較小的情況下，基于打分-搜索的方法MMHC 算法將會收斂到一個更高質量的網絡，且與基于約束的方法相比，基于打分-搜索的因果結構發現方法的探索相對較少，因此其能更好地處理對V 結構的依賴問題。由此算法總體思想是：首先通過SIAPC 算法得到目標節點T的部分父集和子集；然后確定相關的數據集Z進行打分，得到目標節點T的部分父集和子集；之后取二者的交集作為確定的T的父集和子集；最后利用已有的基于限制的方法通過尋找V 結構以及利用Meek 規則來進行修正。

在選取數據集方面，本文目的是選取與目標變量最相關的變量集進行打分，若變量集長度太大則采用打分方法的時間效率很低，長度太小則影響打分結果，因此為了降低時間效率且盡量不損失精度，本文選擇部分數據集Z的方式如下：（1）若SPC(T)長度小于一個給定的參數ss，如果其不為空則選取{SPC(T),T}作為新的數據集Z，否則選取{CSet(T),T}作為新的數據集Z；（2）若SPC(T)長度大于ss，則選取PC(X)（X∈PC(T)）的并集作為新的數據集Z；（3）最后得到的新的數據集Z需要滿足|Z|＞zs，若不滿足，則加入PC(X)到新的數據集中（X∈Z）。對于ss和zs的選取問題，本文進行人工選取然后用實驗進行測試，其中ss選用10、20、30、40，得到ss=20 的實驗結果較好；對于zs，本文選用4、5、6、7，得到zs=5 的實驗結果較好。

2.3 基于打分和限制相結合的混合局部因果結構學習算法

本文規定ID表示其他變量相對于目標變量的因果識別[12]，若T是目標變量，X是其他變量且X∈PC(T)，則ID(X)=1 說明X相對于T來說，X是T的直接原因，ID(X)=2 說明X是T的直接結果，ID(X)=3 說明X與T直接相連，但是方向不確定。本文提出基于打分-搜索方法和基于限制方法結合的混合局部因果結構學習算法HLCS，如算法2。

算法2HLCS

輸入：數據集DATA，目標變量T，獨立性指標w0，數據集選取參數ss和zs。

輸出：PA為T的父節點集，CH為T的子節點集，UN為T的未定向節點集，PC為T的PC 集。

算法3HLCS_sub

輸入：數據集DATA，目標變量T，當前ID，獨立性指標w0，數據集選取參數ss和zs。

輸出：ID相對于T的因果識別。

3 實驗及其結果

3.1 數據集

為了驗證算法的有效性，本文選取https://pages.mtu.edu/～lebrown/supplements/mmhc_paper/mmhc_index.html 上的10 個基準網絡數據集作為測試數據，具體信息如表1。

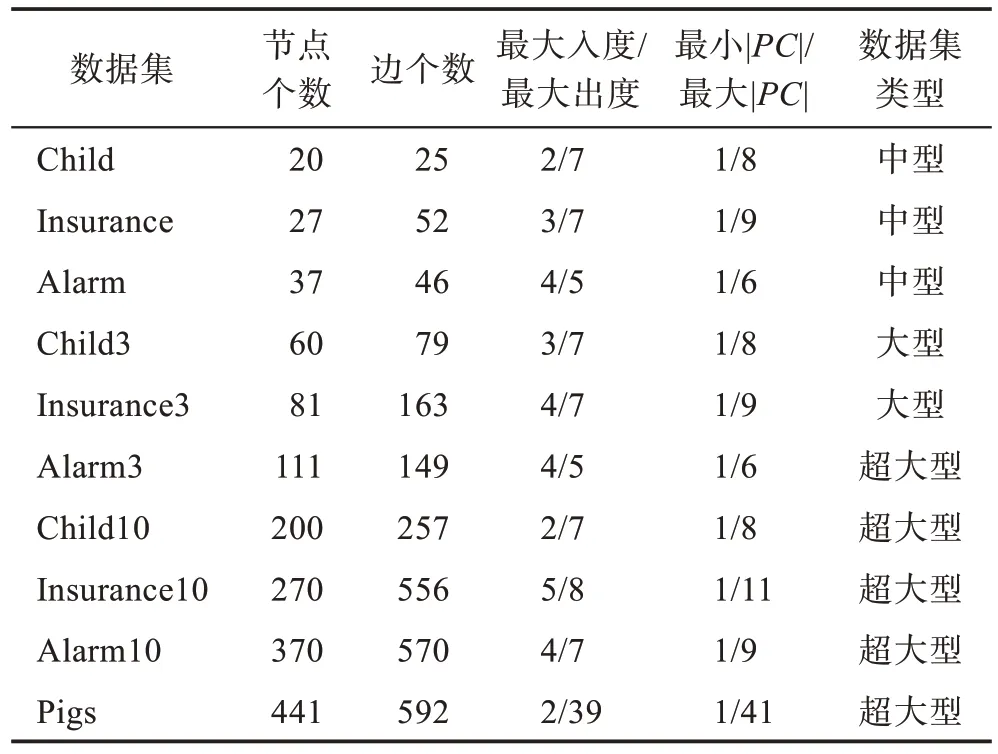
Table 1 Data information of 10 benchmark networks表1 10 個基準網絡數據信息

3.2 評價指標

為了評價算法的性能，針對兩組實驗分別給出了不同的評價指標，具體如下：

（1）PC 發現算法的評價指標[2]

①Precision：算法輸出正確點的數量（和基準網絡對比）/算法輸出的點的數量。

②Recall：算法輸出正確點的數量（和基準網絡對比）/基準網絡中真正的點的數量。

③F1：(2×Precision×Recall)/(Precision+Recall)。

④Distance：

⑤Time：運行每個點的平均時間，單位為秒（s）。

其中③和④表示的是算法的精度，⑤表示算法的時間效率。

（2）局部因果結構學習算法的評價指標[8]

①ArrPrecision：算法輸出中定向正確的邊的數量（和基準網絡對比）/算法輸出的邊的數量。

②ArrRecall：算法輸出中定向正確的邊的數量（和基準網絡對比）/基準網絡中邊的數。

③SHD：算法輸出中定向錯誤的邊的數量（和基準網絡對比）。

④FDR：算法輸出中定向錯誤的邊的數量（和基準網絡對比）/基準網絡中邊的數量。

⑤Time：運行每個點的平均時間，單位為秒（s）。

其中①、②、③、④表示算法的精度，⑤表示算法的時間效率。

3.3 比較算法

（1）PC 發現比較算法

①MMPC：基于拓撲的經典PC 發現算法。

②HTION_PC：基于拓撲的經典PC 發現算法。

③S2TMB_PC：本文提取了基于打分的馬爾科夫毯S2TMB 算法中發現PC 集的過程，命名為S2TMBPC 算法。

（2）局部因果結構學習比較算法

①P_C：一種基于限制的代表性全局因果結構學習算法。

②MMHC：一種基于打分的代表性全局因果結構學習算法。

③PCD-by-PCD：已有的局部因果結構學習算法。

④CMB：已有的局部因果結構學習算法。

3.4 實驗結果

（1）PC 發現比較算法實驗結果

比較算法在樣本數量為5 000 的每個數據集上運行10 次，然后取平均值，實驗結果如表2 所示。

由表2 可以看出，SIAPC 算法與基于限制的方法（MMPC 算法和HTION_PC 算法）相比較，其時間效率很低，但是在精度方面有了很大的改進。與基于打分的方法（S2TMB_PC 算法）比較，在時間效率和精度方面，SIAPC 算法都取得了較好的效果。

（2）局部因果結構學習比較算法的實驗結果

比較算法在樣本數量為5 000 的每個數據集上運行10 次，然后取平均值，實驗結果如表3 所示。

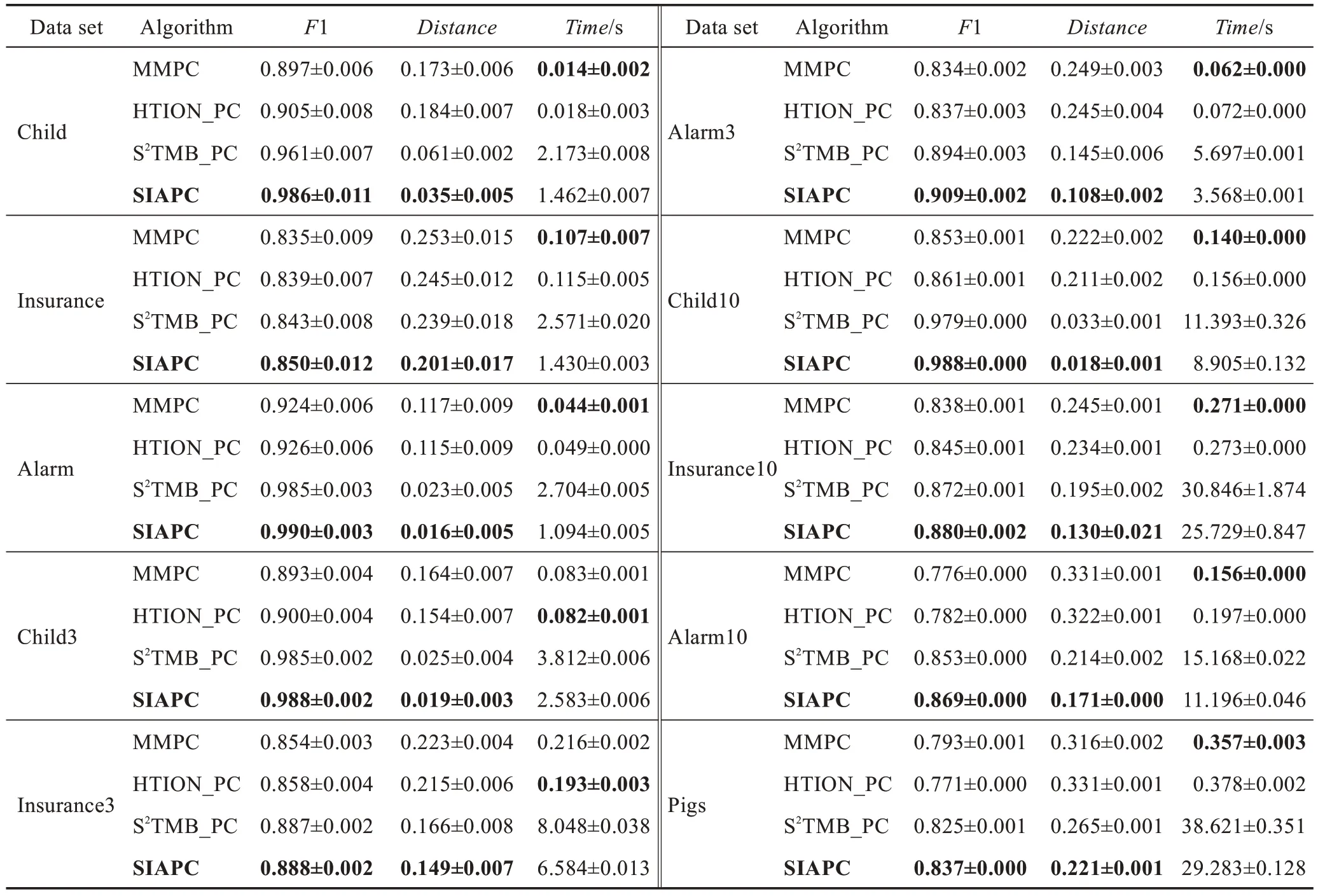
Table 2 Performance comparison of 4 PC discovery algorithms(size=5000）表2 4 種PC 發現算法的性能比較（size=5 000）

由表3 可以看出，算法HLCS 相較于已有算法，在精度方面有較大提升，但是在時間效率方面有相對較大的不足，但是因為本文主要針對的是局部因果結構算法的精度，對時間效率方面的改進將是下一步改進的內容。

HLCS 算法與全局因果結構學習算法（P_C 算法、MMHC 算法）相比較，在精度方面明顯優于P_C算法和MMHC 算法很多，在時間方面也優于這兩種算法。HLCS 算法與局部因果結構學習算法（PCDby-PCD 算法、CMB 算法）進行比較，在精度方面優于PCD-by-PCD 算法和CMB 算法，但是在時間效率方面有相對較大的不足。

3.5 數據量對局部因果結構學習算法的影響

本節說明當樣本數據量不充分時，本文算法相對于已有的局部因果結構學習算法的比較情況。表4為在樣本數量為500 時，算法的實驗結果。而在表5中，將分析局部因果結構學習算法在數據量為5 000時的精度相較于數據量為500 時的精度的增長率，從而說明樣本數據量的大小對算法的影響。

設定以下兩個指標：

其中，RP表示算法在size=5 000 的數據量下ArrPrecision精度相對于在size=500 數據量下ArrPrecision精度的增長率；RC表示算法在size=5 000 的數據量下ArrRecall精度相對于在size=500 數據量下ArrRecall精度的增長率。表5 中的數據值越大，說明算法受數據量的影響越大。

從表4 可以看出，在數據相對不充分的條件下，HLCS 算法的精度相較于其他兩個局部因果結構學習算法較好，但是時間效率相對不足。從表5 和圖4中可以看出，隨著數據集的增加，HLCS 算法的增長率最低，說明該算法可以有效緩減數據充分性。

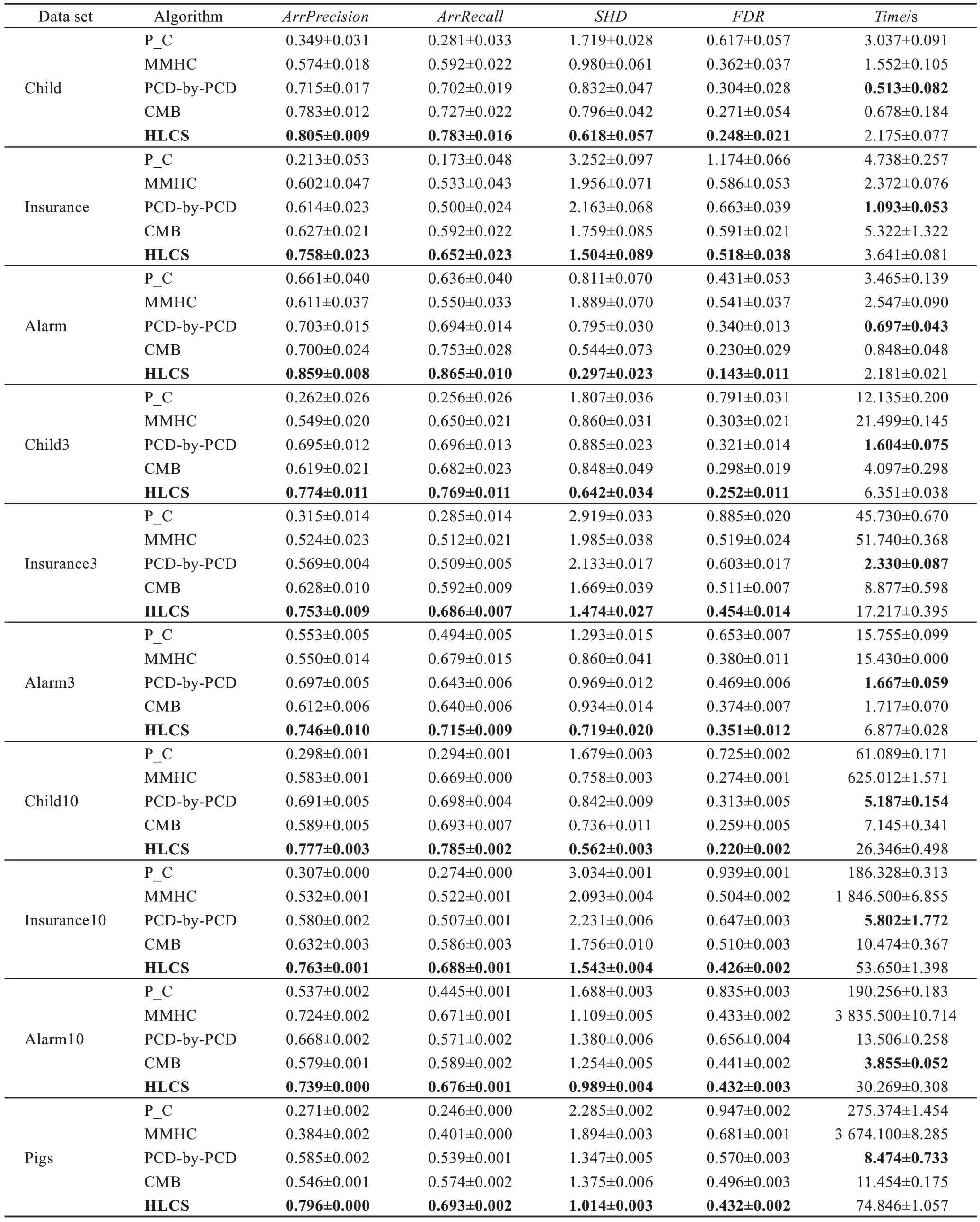
Table 3 Performance comparison of 5 local structure learning algorithms(size=5000)表3 5 種局部結構學習算法的性能比較（size=5 000）

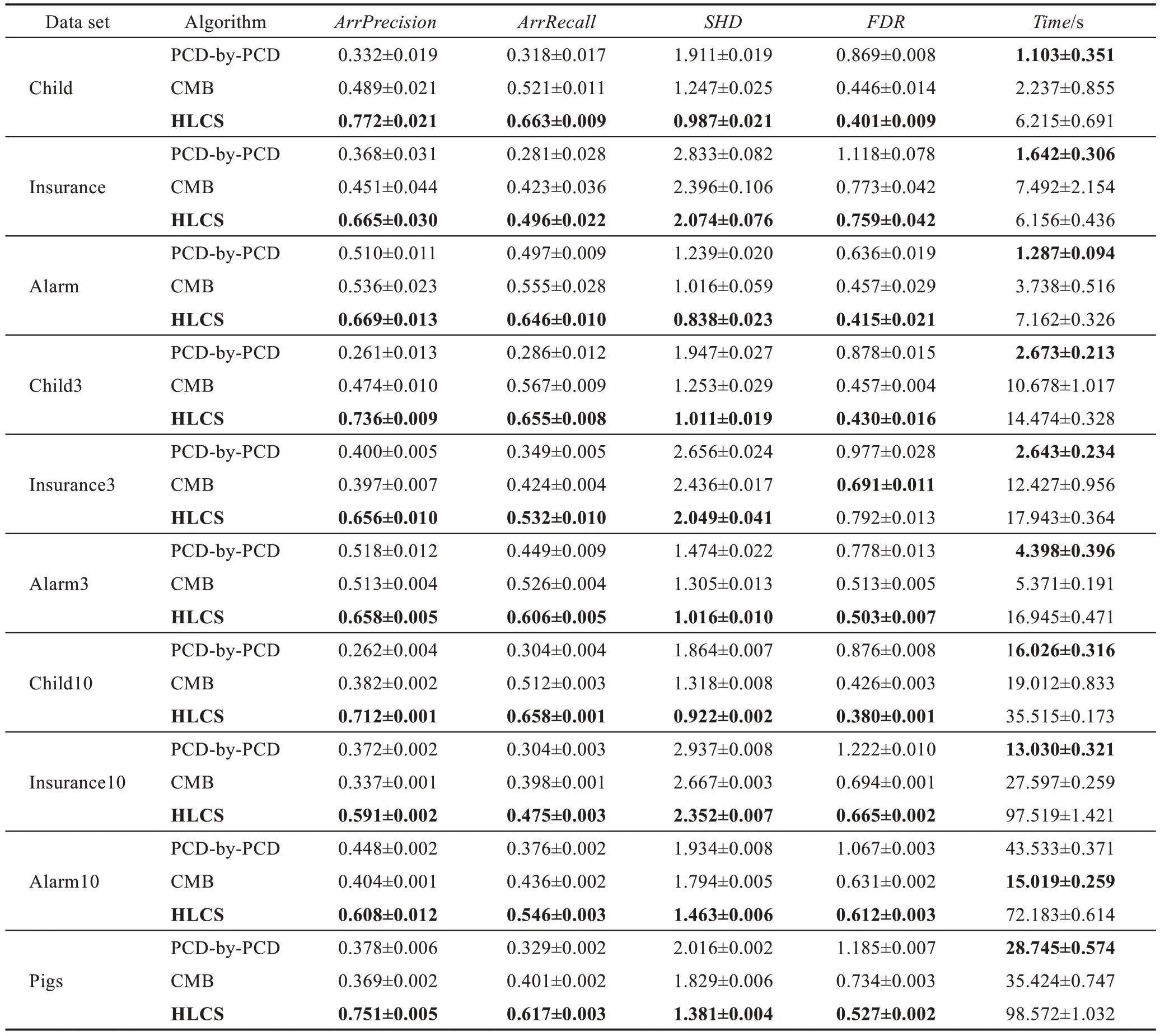
Table 4 Performance comparison of 3 local structure learning algorithms(size=500)表4 3 種局部結構學習算法的性能比較（size=500)

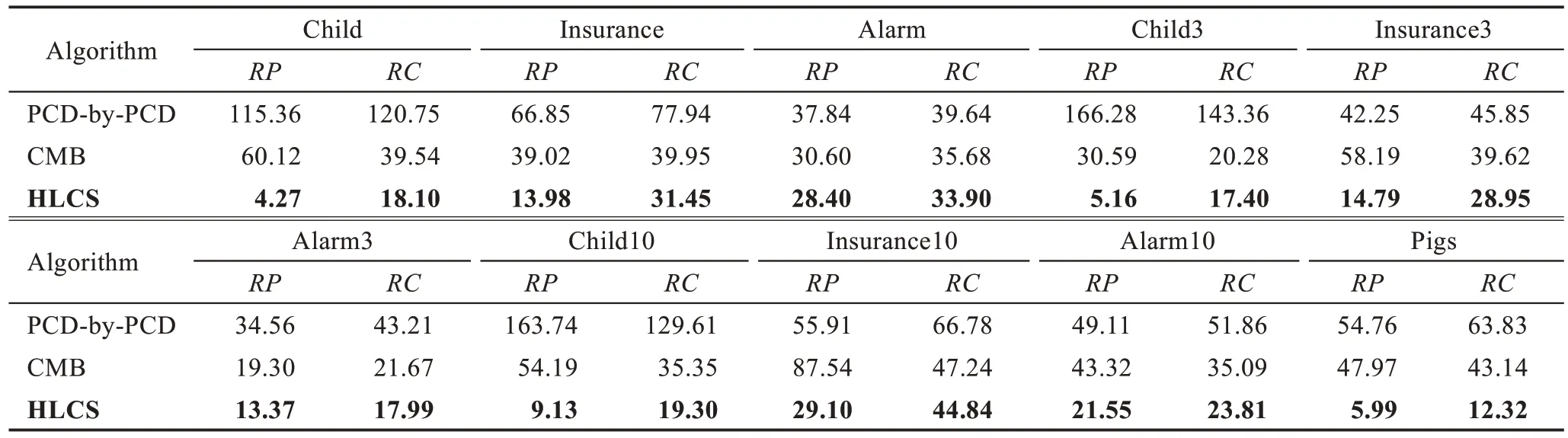
Table 5 Growth rate of accuracy of algorithms at size=5000 compared with size=500表5 算法在size=5 000 時對size=500 時精度的增長率 %

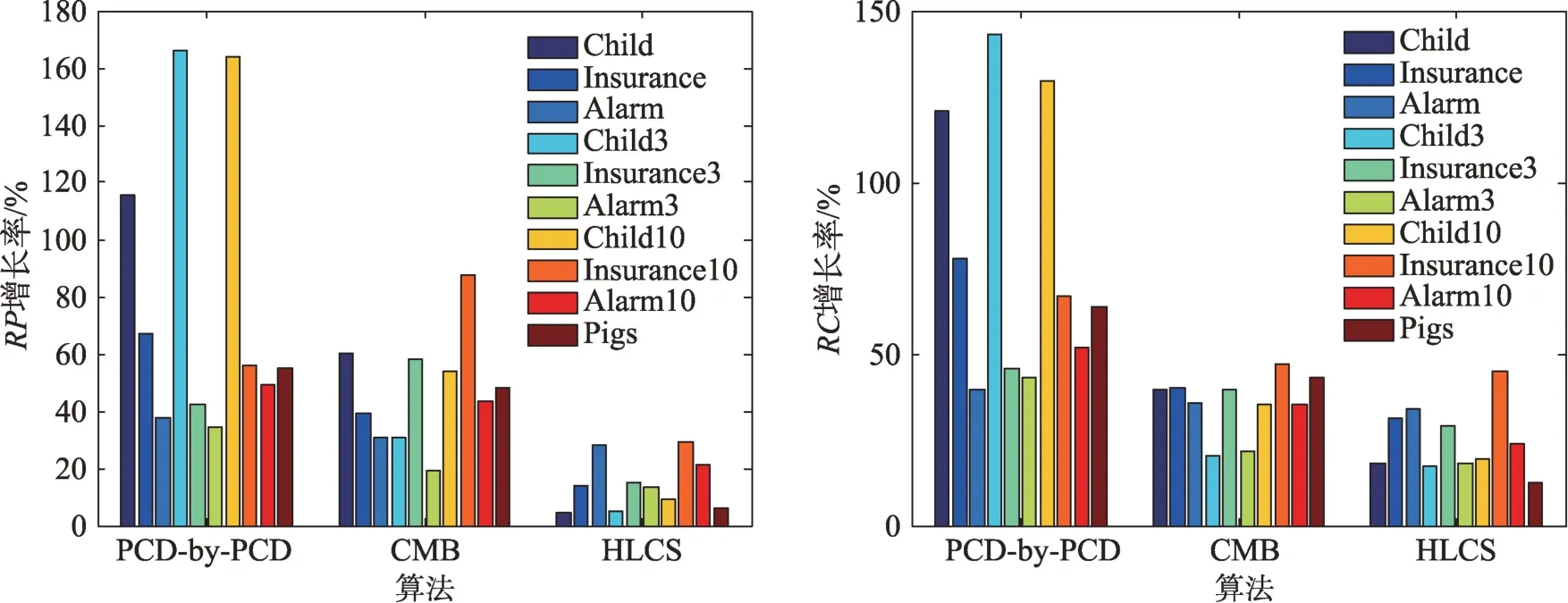
Fig.4 Growth rate of RP and RC of algorithm at size=5000 compared with size=500圖4 算法在size=5 000 時對size=500 時RP和RC的增長率

4 結束語

本文針對已有算法的定向結果依賴目標變量的MB/PC，以及其結果取決于V 結構的發現的問題，提出一個基于打分和限制相結合的混合局部因果結構學習算法——HLCS 算法。該算法在步驟1 提出了基于打分和限制相結合的PC 發現算法，有效地提高算法精度；在步驟2 利用PC 發現算法得到的定向結果和對部分數據集打分得到的定向結果的交集來確定邊的方向，然后使用條件獨立測試進一步修正邊的定向結果，該方法可有效降低對V 結構的依賴性。同時因為步驟1 和步驟2 都是結合基于打分的方法進行的，所以HLCS 算法可以有效緩減數據效率問題。實驗驗證，在標準假設下，本文算法相較于已有的算法在精度方面有較大的提高，但是由于打分方法的低效性，提高時間性能是下一步的研究工作。