船舶加筋板輕量化設計研究

黃陳哲，向 陽，黃進安

(1. 武漢理工大學 能源與動力工程學院，湖北 武漢 430063；2. 武漢理工大學 高性能艦船技術教育部重點實驗室，湖北 武漢 430063)

0 引 言

在世界各國經濟不斷發展的同時，對能源的需求也日益增多[1]，航運業是聯系各國貿易的重要紐帶，但同時也是耗能大戶，如何提高船舶能效，減少污染成為了目前亟待解決的問題。有研究表明，減少船舶的整體重量，不僅能夠有效提高船舶能效，還能減少建造船舶鋼材的使用[2]。而在輕量化的過程中必定會存在舶結構強度不夠、安全系數降低、某些部位振動劇烈甚至振裂等安全問題，因此在保證安全參數不下降的情況下，減輕船舶的重量就成為了研究焦點。

加筋板作為船舶中的基本結構單元，對其開展輕量化設計研究并推廣，將有助于全船整體重量的減少，達到全船輕量化的目的。加筋板的強度是其重要安全指標之一，大量的實驗研究[3]和模擬研究[4]討論不同變量參數對極限強度的影響，也有的通過研究解析解的方式探究其強度變化規律[5]。所以以強度為核心參數的結構優化是研究重點，Singh 等[6]開展了加強筋位置優化，利用曲線加強筋代替原均布直線的布置，Badran 等[7–8]研究并設計了一種新型的Y 型加強筋剖面，能夠提供更多的抗扭轉強度。除了力學特性，振動特性同樣也是加筋板的重要特性之一，張文春等[9]就運用模態疊加法對縱向混合構型加筋板在線激勵作用下振動特性開展了相關研究工作，同樣也有學者以振動控制為目標的結構優化研究[10]。

在結構優化研究中，一般只考慮力學特性或振動特性其中之一，鮮有同時考慮振動與重量的結構優化研究，而船舶的加筋板要保證一定強度同時，對振動控制也有一定的要求。而在結構優化中，重量、強度、剛度三者間相互關聯，互相影響，為了能夠實現輕量化和振動的協同設計，在力學分析的基礎上加入單位激勵的諧響應分析，并約束分析頻段內的最大位移值，在優化后的校核計算中也將自由模態頻率的分布情況作為校核的重要指標，以達到協同設計的目的。

如圖1 所示，本文基于OptiStruct 結構優化軟件，采用拓撲優化和尺寸優化相結合的方法，全面考慮加筋板的力學和振動特性，以最小重量為目標，對加筋板結構開展輕量化與振動的協同設計。根據優化結果和實際生產需求重構模型，并與原加筋板進行對比，驗證優化結果的有效性。最后將詳細分析腹板與底板的夾角大小對新型加筋板特性的影響。

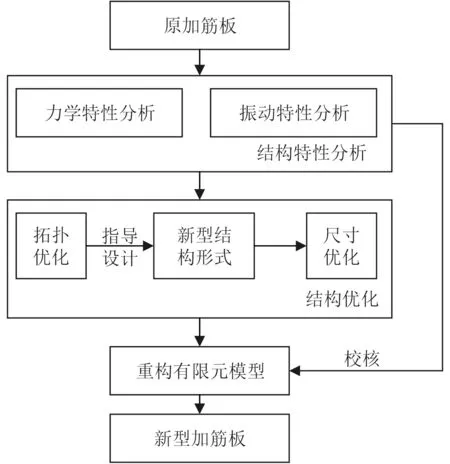
圖1 結構優化流程示意圖Fig. 1 Structure optimization process

1 優化基本理論

基于OptiStruct 軟件開展加筋板輕量化設計研究，其優化過程分為拓撲優化和尺寸優化兩步，與概論設計和詳細設計2 個階段相對應，通過拓撲優化改變拓撲結構，設計新型加筋板結構形式，再進行尺寸優化，尋找約束條件下尺寸參數的最優解。

1.1 拓撲優化

拓撲優化采用變密度法進行求解，材料的固有屬性與材料密度定義為非線性關系。在拓撲優化過程中，定義優化區域內的材料密度分布在0～1 之間，通過查看優化后材料的分布情況，指導優化設計工作。材料的密度和彈性模量的非線性關系可以表示為如下關系[11]：

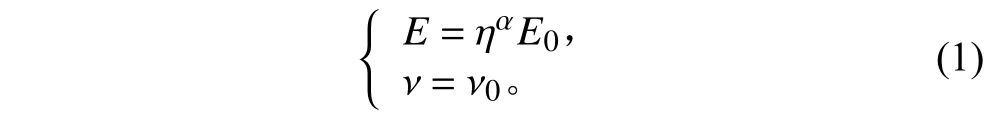
式中： η為單元的密度； α為懲罰因子；E為改變密度后材料的彈性模量； ν為泊松比；E0和 ν0為原材料的彈性模量和泊松比。

拓撲優化以最小質量為優化目標，考慮平衡方程和約束條件，尋找最優材料密度分布。計算過程中通過改變優化區域內單元密度，迭代計算。經過拓撲優化后，設置合適閾值，刪除材料密度小于閾值的單元，從而形成新的拓撲結構。其優化模型為下式：

式中： ηi為單元的密度；V0為材優化區域內對應單元體積；Yi為約束變量，表示第i個工況下有限元計算的最大應變或應力；Ymin,Ymax為約束變量的上下限； ε為密度下限；J1,J2,···,Jk為優化后單元密度保持不變的單元號；最后一式為結構平衡方程；K為結構的整體剛度矩陣； {δ}為 結構的整體位移列陣；F為結構所受的整體載荷。

輕量化與振動的協同設計就是在優化過程中，將振動分析的響應值合理引入到約束變量Yi中，并對其進行約束，從而使得振動在輕量化過程中得到合理的控制。

1.2 尺寸優化

尺寸優化對應產品詳細設計階段，其設計變量與剛度矩陣一般為簡單的線形關系，優化變量一般為構件的尺寸參數。式（3）為尺寸優化的數學模型。

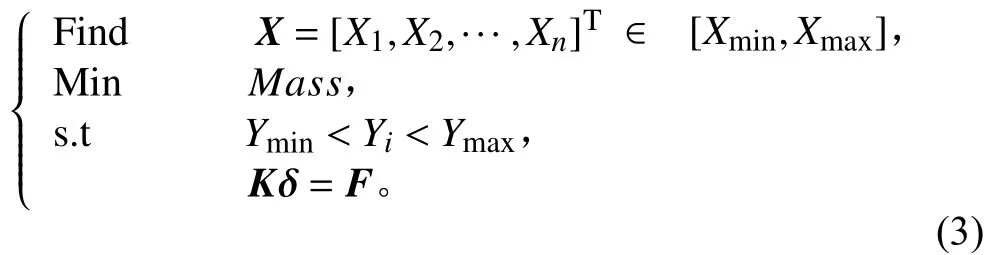
式中：X為設計變量；Xmin,Xmax為變量的上下限；Mass為質量，Yi約束變量；Ymin,Ymax為約束變量的上下限。

2 結構特性分析

加筋板是船舶的基本結構單元，開展結構優化設計工作前，首先需要對加筋板的特性進行分析，并以此作為后續優化的參考和約束。以某船舶上層建筑為研究對象，截取了一段包括3 條L 型加強筋的板，具體尺寸如圖2 所示。

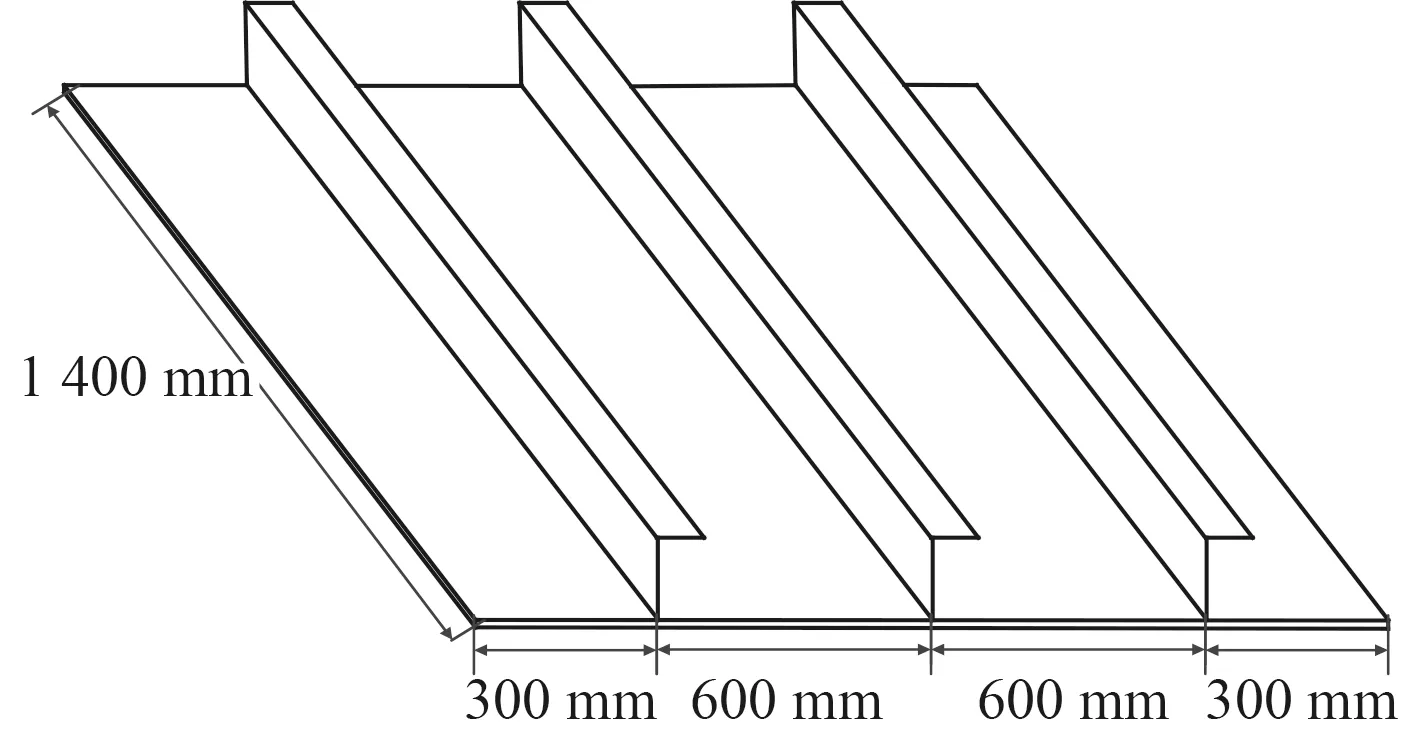
圖2 加筋板示意圖Fig. 2 Stiffened plate

底板厚6 mm，L 型材的尺寸為75×50×5。有限元模型全部采用PSHELL 殼單元，其中網格尺寸最大20 mm，為提高局部計算進度及到后期的優化工作，將加強筋處的網格細化到5 mm。板材和加強筋的材料為鋼材，彈性模量210000 MPa，泊松比0.3，密度7.85*10?9mm3/t，臨界阻尼比0.03。為了模擬截斷加筋板的邊界，分別在四條邊上創建了4 個中點，將網格的邊界點與此點通過剛性單元綁定，如圖3 所示。

圖3 加筋板有限元模型Fig. 3 Finite element model of stiffened plate

如表1 所示，一共分析了10 個工況，其中前6 個工況分析板材抗外力的能力，是板材強度的體現；工況7 和工況8 是屈曲強度分析，體現了板材整體的穩定性；最后兩工況分別計算了自由模態和諧響應，代表了板材振動特性。經過有限元計算后，將計算結果匯總到表1 中的計算結果。

如表1 所示，在強度分析中，均布載荷使得加筋板產生了較大形變和應力，將作為后續拓撲優化應力約束的參考。由于加強筋是單向的，所以2 個方向的抗扭轉能力和屈曲強度呈現較大差距，后續優化過程中將對2 個方向分別約束，避免過約束或欠約束。振動分析中，諧響應的最大振幅對應頻率與第2 階模態頻率相近，兩者存在一定的關聯，但單一的模態頻率或諧響應來表征振動特性不夠全面，因此2 種振動分析都是必不可少的，也是后續協同振動控制結構優化的重要約束條件。

表1 詳細工況及計算結果匯總表Tab. 1 Summary of detailed operating conditions and calculation results

3 優化設計及結果討論

通過結構特性分析得到的應力應變、屈曲強度和頻率特性分別表征了板材的強度和振動特性，各個工況下的計算值將作為后續優化過程中的約束條件，進一步開展結構優化研究。結構優化在滿足原板性能不降低的約束下，以最小質量為優化目標，通過拓撲優化得到材料分布情況，從而指導重新設計新型結構形式，在根據尺寸優化結果確定最終板材厚度。

3.1 結構優化

由于船舶中加強筋的布置距離與船舶肋距相關，所以選定3 條加強筋所在的立方體空間為拓撲優化空間，同時設置了對稱約束和拔模約束，如圖4 所示。為提高優化精度，對優化區域的網格進行了加密處理，網格尺寸為5 mm。

圖4 加筋板有限元優化模型Fig. 4 Finite element optimization model

由于拓撲優化屬于概論設計階段，優化結果僅作為后續設計的指導，因此可以適當放寬約束條件，從而使得計算更容易收斂，優化效率提高。在拓撲優化中，對應變施加強制約束，將應力轉換為參考約束，即優化過程中允許有少量網格的應力大于約束值。表2 為各工況下具體約束的大小，應變最大放寬不超過0.2 mm，屈曲強度放寬不超過10%，而為了能夠更好控制振動，對諧響應工況下的最大位移約束提高了約10%。

圖5 為拓撲優化結果局部圖。其頂部和兩側區域材料較為重要，中心部分的材料被掏空，所以將其設計為空心的加強筋，兩側相對于頂板來說存在一些挖空部分，能夠通過挖孔的方式進一步降低重量。考慮到實際的加工需要，先不對側邊進行鏤空處理。

根據拓撲優化結果，重新設計了圖6 所示的加強筋形式。新結構保持高度和頂板寬度不變，腹板與底板之間的角度為45°，并且除去了底板。經過計算發現，去除底板導致垂直于加強筋方向的屈曲強度大大降低，而增加少量支撐能夠大幅提高屈曲強度。因此

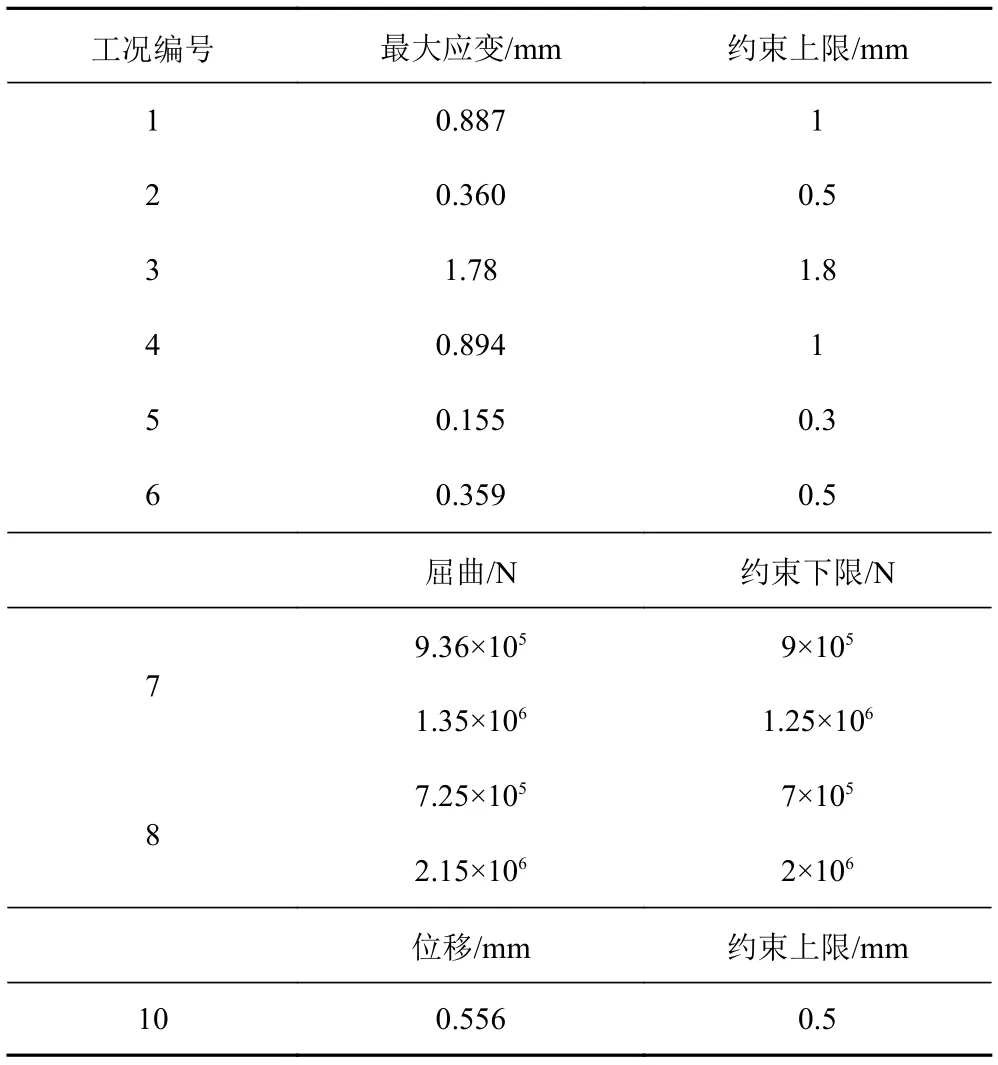
表2 拓撲優化約束Tab. 2 Topology optimization constraints

圖5 加筋板拓撲優化結果Fig. 5 Topology optimization results

圖6 梯形加強筋局部Fig. 6 Part of trapezoidal stiffened plate

構建了如圖7 所示有限元模型，去除底板后增加了3 塊均布的支撐板。腹板與底板之間的角度將在后續做詳細的討論。

根據拓撲優化結果建立模型后，利用尺寸優化進行加筋板的詳細設計，以確定最終尺寸參數。尺寸優化設定更嚴格的約束條件，以保證最終優化的有效性，具體約束如表3 所示。由于底板表面積降低，均布壓力值調整為0.014 MPa，使得總體載荷值略大于之前的載荷，以保證優化有效性。在一般工程應用中，達到第1 階屈曲值后，就已經對結構產生了破壞，所以只約束第1 階屈曲強度。

圖7 輕量化加筋板有限元模型Fig. 7 Lightweight stiffened plate finite element model

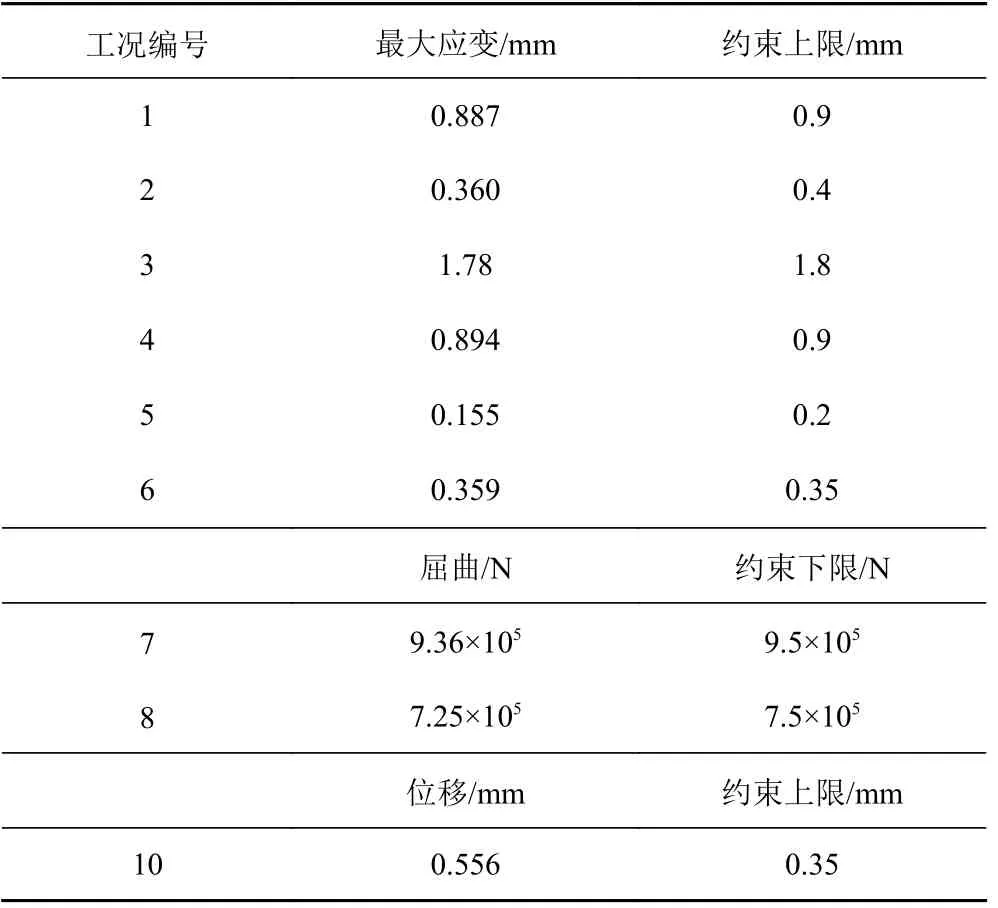
表3 尺寸優化約束Tab. 3 Size optimization constraints

如表4 所示，優化前尺寸參照原加筋板尺寸設定（面板5 mm，L 型材75×50×5），上下限是在原尺寸的基礎上上下浮動。經過尺寸優化后，得到表中優化后尺寸，考慮到實際制造過程中使用沖壓工藝造價更低，最終確定為厚度5 mm 的均質板。

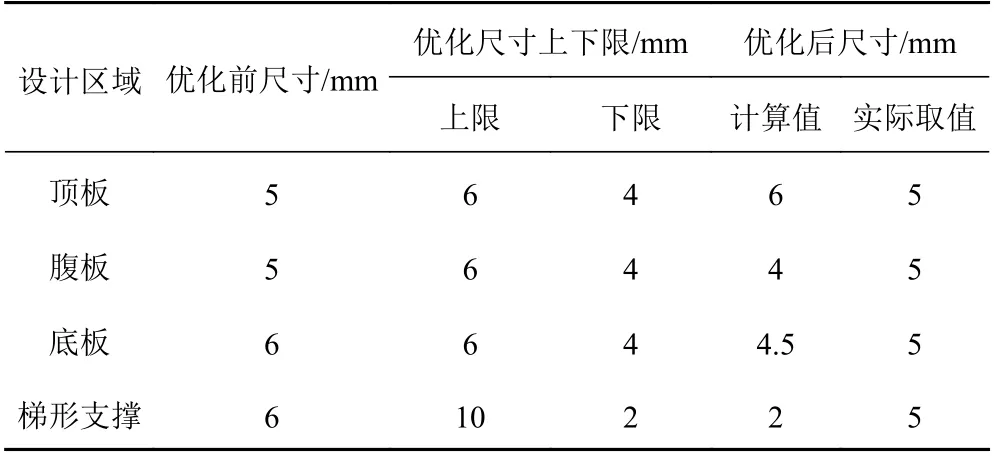
表4 尺寸優化變量參數及優化結果Tab. 4 Variable constraints and optimization results

3.2 優化結果討論

根據表4 中尺寸優化結果，重構有限元模型，在保證載荷不降低的前提下，適當調整載大小和施加位置，重新對比分析各工況下的優化后加筋板的特性參數，將最終的計算結果匯總到表5。

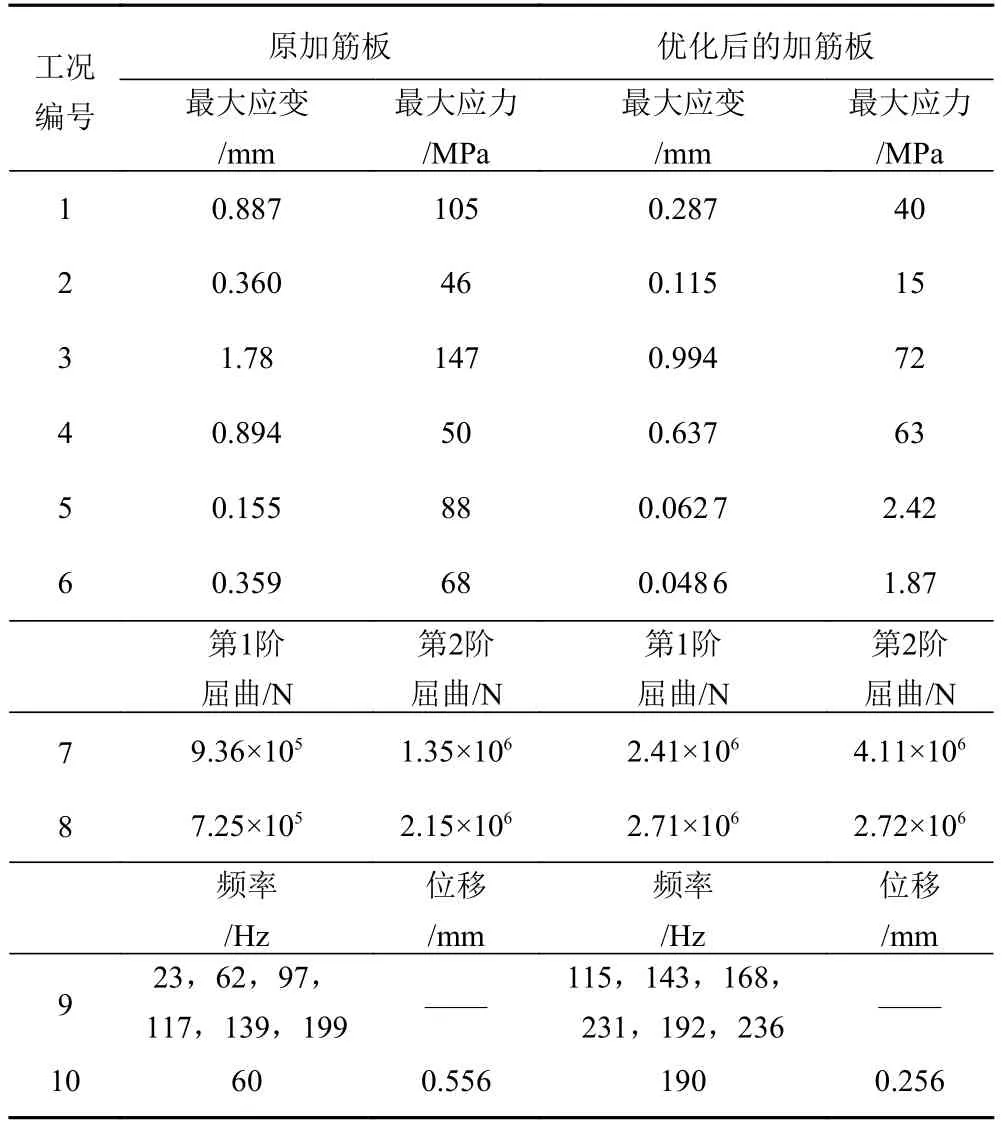
表5 優化前后特性對比Tab. 5 Performance comparison before and after optimization

如表5 所示，所有工況下最大應變值都小于原加筋板的計算值，除工況4 的最大應力增大了13 MPa 以外，其他工況的最大應力都有所減少，2 個方向的屈曲強度也有顯著提升，固有頻率增大，在諧響應工況下，最大位移降低了0.3 mm，板的質量由原139.3 kg降低到112.5 kg，在原基礎上減少了19.2%的重量。工況4 中應力出現了大于原加筋板的情況，這是因為板整體厚度比原加筋板減少1 mm，導致點載荷施加在薄板處后，應力出現了增大的情況，但是應變比原加筋板有所減小，所以認為在此工況下為優化后強度沒有降低。

在振動特性分析中，優化后模態頻率排列與原加筋板同階振型對應，相同振型對應頻率的增加間接說明了加筋板整體剛度的增加質量降低，固有頻率向高頻方向的移動使得建造后上層建筑的振動很容易控制。在諧響應分析中，最大振動位移降低0.3 mm，即振動位移級峰值降低6 dB，顯示了振動控制的有效性。

總體上，優化后的加筋板不僅具有較輕的重量，而且具有較高的強度和良好的振動特性，能夠廣泛適用于船舶的上層建筑。但由于面板不完整和對點載荷較敏感的特點，也具有一定的局限性，不適用于船舶外殼和機艙等位置。

4 腹板與底板的夾角對板材特性的影響

在新型加筋板設計中，腹板與底板的夾角是所有參數中影響最為復雜的參數，也是影響新型板性能的重要參數，故將對其進行詳細對比分析研究。有限元分析中，所有板材均為5 mm，保持頂板寬度及梯形高度不變，以腹板與底板之間的角度α 作為變量，如圖8所示，虛線為改變α 后腹板的位置。

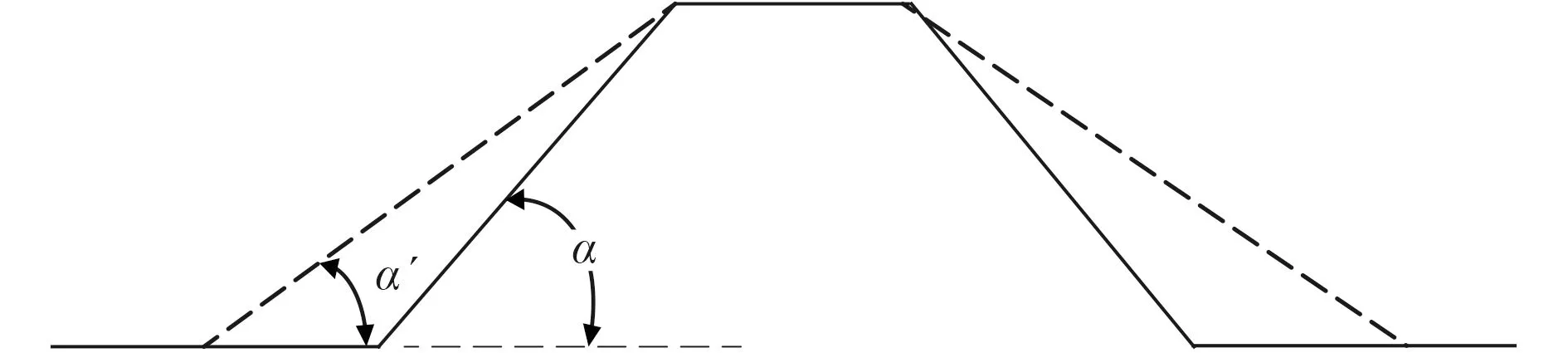
圖8 梯形加強筋局部示意圖Fig. 8 Part of trapezoidal stiffener

如圖9 所示，隨著角度的減小，整體重量而減少，變化率略微降低。由于整體厚度的下降，夾角即使在90°的情況下，也相比于原板降低10.2%。

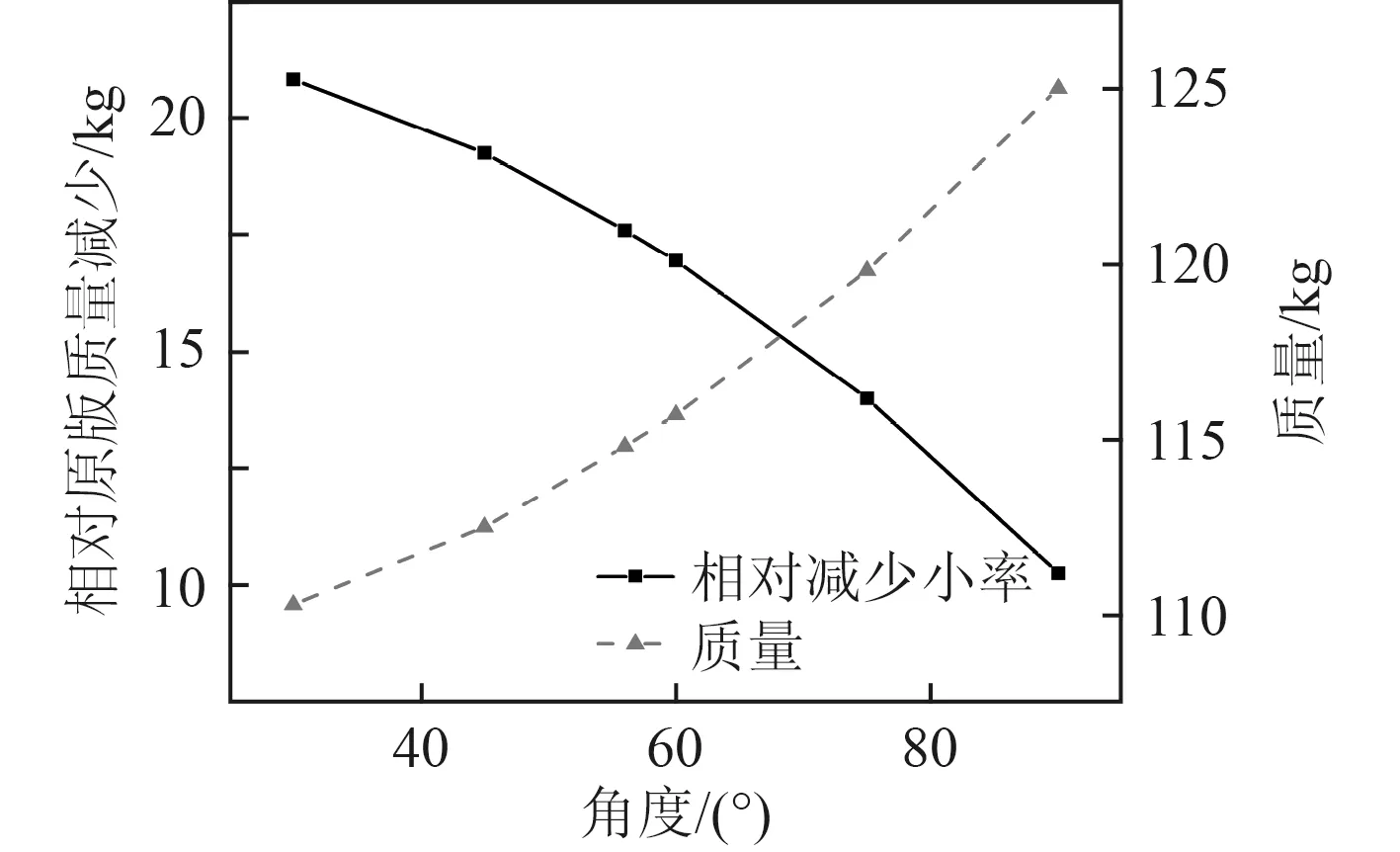
圖9 質量變化曲線Fig. 9 Curve of weight change

圖10為最大應變隨角度變化曲線圖，工況1 和工況2 趨勢相同，工況5 和工況6 趨勢相同，故只展示變化明顯的4 個工況。隨著角度增加，工況3、工況4和工況5 的最大應變呈總體呈上升趨勢，而在工況2的最大應變先略微下降后增加。

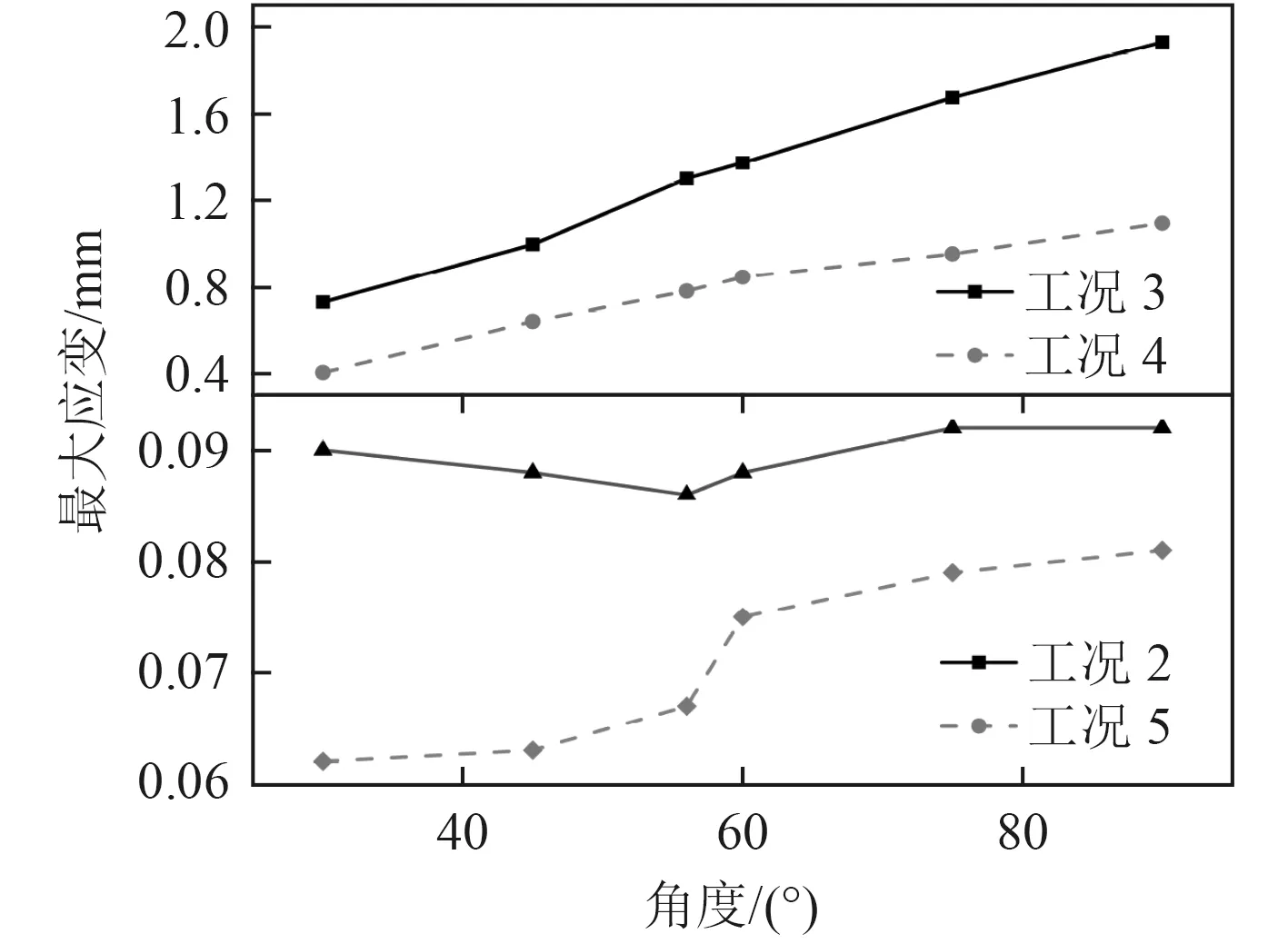
圖10 最大應變曲線Fig. 10 Maximum strain curve

圖11為最大應力隨角度變化曲線圖，由于工況1、工況2 與工況5 趨勢相同，所以不予展示。在均布載荷的作用下，夾角為60°使最大應力突然減小，這是由于隨著夾角的增加，底板面積逐漸增大，為保持總載荷不變，單位面積載荷減小，而角度的增加，也使得腹板對垂直于底板方向的支撐增強，因此出現了突變，這也導致了除工況4 以外其他工況在60°附近存在一個最大應力極小值；而隨著角度繼續增加，面積增加所帶來的強度降低更加顯著，故呈小幅上升趨勢。總體上，角度對板材各工況下的強度影響輔助，小角度將有助于提高板材的整體強度。

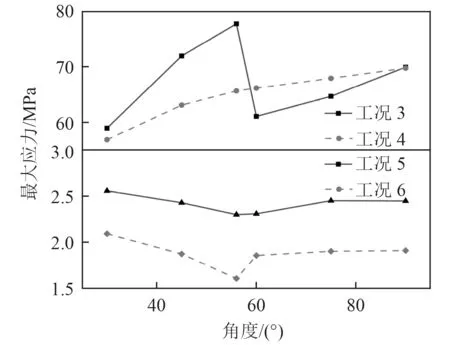
圖11 最大應力曲線Fig. 11 Maximum stress curve

如圖12 所示，在屈曲分析中，角度從30°增加到45°垂直加強筋方向的屈曲強度大幅度增加，另一個方向的屈曲強度則大大降低，而隨著夾角的繼續增加，兩者均略微有所下降，因此較小角度會導致一個方向屈曲強度大大降低，穩定性大大降低。

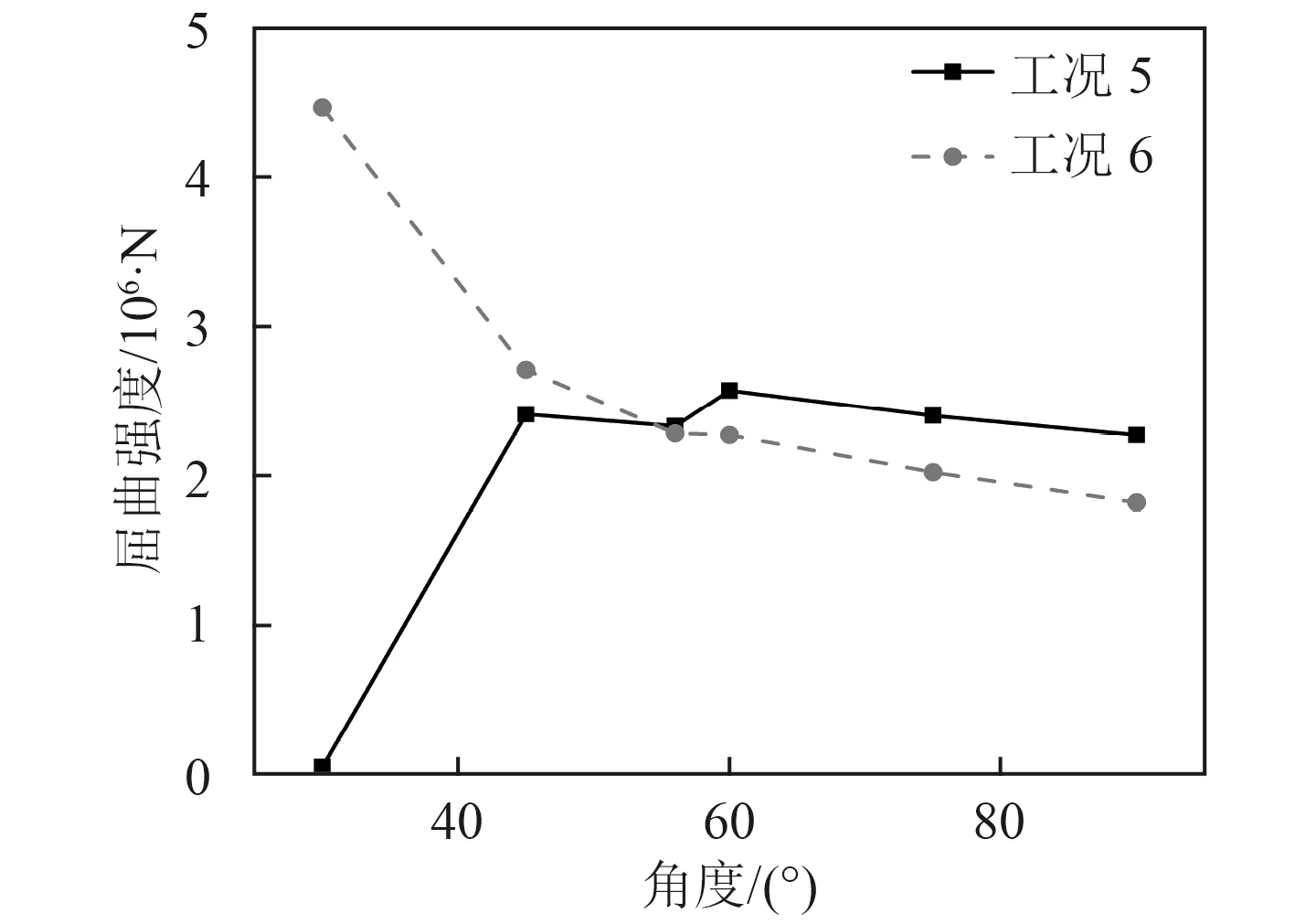
圖12 屈曲強度曲線Fig. 12 Curve of buckling strength

圖13為相同振型的頻率變化和諧響應分析峰值頻率和位移曲線。其中最大振動位移隨角度增加而增加，增長率也有所提高，3 個相同振型的模態頻率隨著角度的增加而降低。曲線變化情況反映了板材剛度隨角度的增加而減小，這與底板面積的增加而帶來的相對剛度的降低和質量的增加時密不可分的。

圖13 模態頻率變化和諧響應最大位移曲線Fig. 13 Maximum displacement curve of harmonious response of modal frequency change

綜上分析，夾角為45°時，重量、振動都得到了很好的控制，2 個方向的屈曲強度也處于較高水平，強度總體滿足需求。

5 結 語

以船舶上層建筑的加筋板為研究對象，開展了輕量化設計研究工作取得了以下成果：

1）在整體強度不降低前提下，實現減重19.2%，底板中心激勵的振動最大位移級峰值降低6 dB，實現了加筋板的振動控制和輕量化協同設計。

2）采用拓撲優化和尺寸優化相結合，在優化約過程中引入諧響應分析，并約束分析頻段內的最大位移值能夠有效控制振動，可避免輕量化所帶來的振動加劇的問題。

3）采用上述方法，對局部特定工作條件下的結構開展結構優化將獲得更好的效果。