基于BP-GA 算法的環肋錐柱殼多目標優化設計

李艷萍，黃小平

(上海交通大學 船舶海洋與建筑工程學院，上海 200240)

0 引 言

潛艇具有偵察、攻擊、掩護等多種功能，是大國海軍不可或缺的戰略性武器。潛艇耐壓結構是潛艇的主體結構，是保證潛艇強度、穩定性、速度等全艇性能的重要保障，故潛艇耐壓結構的優化設計十分重要。

以往潛艇、潛器的優化設計像潘濤[1]、王燕[2]大多都是追求重量最輕的單一目標，而結構重量越輕，穩定性卻也會越差。對于大型潛艇來說，設法提高穩定性十分重要。將重量與穩定性綜合考慮，既能減少造價、更易控制重量分配，同時也能提高艇體安全性，便于適合高強度材料的使用。對于多目標優化問題，經典的求解方法有加權法、約束法、目標規劃法和極大極小法等，優化權重系數不論是由決策者確定，還是由優化方法自動調整，都存在著局限性[3–4]。采用多目標遺傳算法獲取Pareto 最優解組，再利用最小距離法[5]選取最優解，可以克服上述不足。

由于探潛技術水平的不斷提升，潛艇采用大潛深、超大潛深技術是提高其隱蔽性的重要途徑之一，這樣甚至能有效地規避反潛武器的攻擊[6]。鈦合金是一種廣泛用于潛艇上的優質新型材料，它具有重量輕、強度大、耐腐蝕、生物兼容性好等諸多優點[7]。潛艇本身屬于大型結構，其每次的穩定性分析都涉及大量計算，若直接采用有限元軟件進行分析優化，需要反復循環求解新的迭代方程，其時間成本過大，不具有可操作性[8]。運用BP 神經網絡的非線性映射關系代替有限元方法計算的迭代方程式進行分析，其效率高，精度好，且遺傳算法具有并行性、隨機性、全局化等優點，與BP 神經網絡優勢互補。因此，本文采用BP 神經網絡與遺傳算法聯合優化（以下簡稱BPGA 算法）方法，研究最大下潛深度達600 m 的超大潛深潛艇，且采用新型材料鈦合金的耐壓艇體的優化問題，更加具有實用性。

1 殼體結構的主要參數確定

以某級潛艇數據為母型，其最大排水量16 000 t，采用雙殼體設計，最大航速可達32 kn，其潛深可以達到600 m[9]。本文潛艇數據取排水量16 000 t，儲備浮力系數為0.3，最大下潛深度為600 m。

1.1 主尺度估算

根據陳明高等[10]常規潛艇排水量和主尺度的確定新方法中排水量表達式：

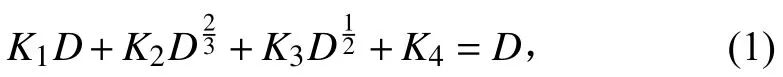
計算潛艇的主尺度：

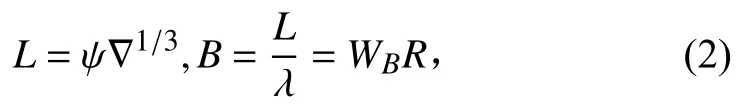
導出計算表達式：

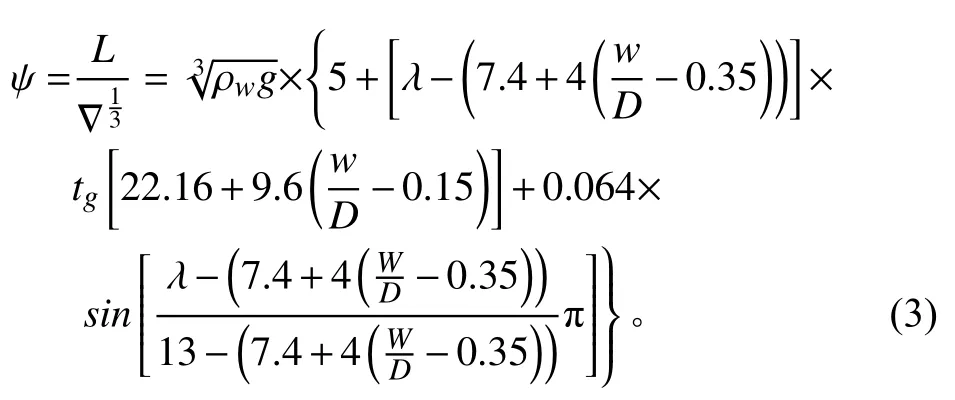
其中： ρω為海水密度；λ 為長寬比值；ω 為儲備浮力；D為排水量；W/D為儲備浮力排水量比。

根據上述計算表達式，給出如表1 所示的主尺度估算結果。

表1 主尺度估算結果Tab. 1 Main scale estimation result

取長寬比為11 的數據，艇首艇尾是標準的水滴型，艇體中段都采用簡單平直的圓型斷面構造，長度大約是該艇長度的80%，錐體傾角為15°，可以得出如表2 所示的主尺度。

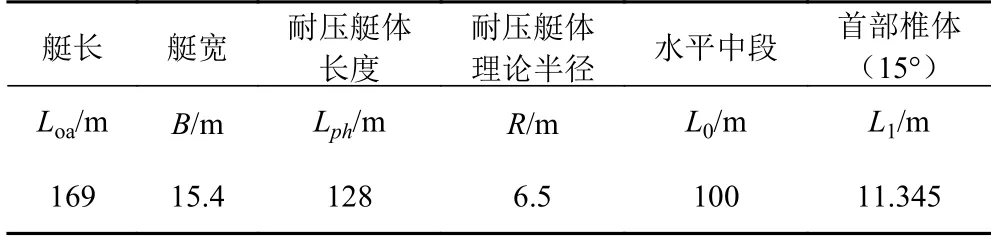
表2 潛艇主尺度Tab. 2 Main scale of submarines

1.2 計算壓力

根據《潛艇》[11]計算可得：

極 限 深 度he=600 m,Pe=5.98 MPa ；

工作深度ho=540 m ；

設計 計算深 度hc=900 m，Pc=8.921 MPa。

1.3 耐壓殼體厚度及殼體材料

根據《規范》[12]中5.2.1 核潛艇殼板中面周向應力的要求初步計算耐壓殼的厚度及肋骨厚度，如下式：

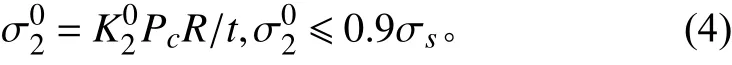
其中：σ02為殼板中面周向應力； σs為材料屈服點。

耐壓殼材料選取比重小、強度高、耐高溫、抗腐蝕性強的TC4 鈦合金，其性質如表3 所示，經計算其厚度初步選取76 mm。

表3 退火鈦合金性質Tab. 3 Annealed titanium alloy properties

雖然鈦合金有著上述諸多優點，然而鈦開發量較少，價格高昂，用作耐壓殼的需求量大，成本高，且鈦合金彈性模量低，變形大。對于和耐壓殼尺寸相比的微小結構—肋骨來說，其結構小，穩定性高，且應力偏小，破壞可能性低，選取價格較為低廉的高強鋼就可以滿足要求。故肋骨選取HY-100 steel，其性質如表4 所示，尺寸根據《規范》[12]初步取為

表4 HY-100 steel 的性質Tab. 4 HY-100 steel properties

2 BP-GA 算法的基本原理

2.1 遺傳算法

遺傳算法是模擬達爾文生物進化論的自然選擇和遺傳學機理的生物進化過程的一種隨機算法模型，是一種基于“適者生存”的高度并行、隨機和自適應的優化算法。它將問題的求解表示成染色體的適者生存過程，通過染色體群的一代代不斷進化，包括復制、交叉和變異等操作，最終收斂到“最適應環境”的個體，從而求得問題的最優解或滿意解[13]。遺傳算法的主要步驟為：編碼，初始群體的生成，適應性值評估檢測，選擇，交叉，變異。其運算流程如圖1 所示。

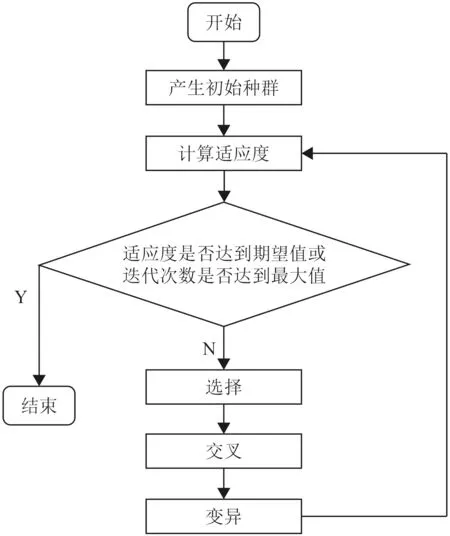
圖1 遺傳算法流程圖Fig. 1 Genetic algorithm flow chart

2.2 BP 神經網絡

BP 神經網絡是一種按誤差逆向傳播算法訓練的多層前饋網絡,其基本思想是梯度下降法，利用誤差反傳，反復學習訓練，使網絡的實際輸出值和期望輸出值的誤差均方差均為最小。神經網絡既是并行處理和大規模平行計算的基礎，又是高度非線性動力學系統和自適應組織系統，可用來描述認知、決策及控制智能行為[14–15]。具有非線性映射能力，擅于從輸入和輸出信號中尋找規律，不需要精確的數學模型，并行計算能力強，易于進行軟硬件的編程計算[16]。BP 神經網絡結構由輸入、輸出、隱含層組成，如圖2 所示。

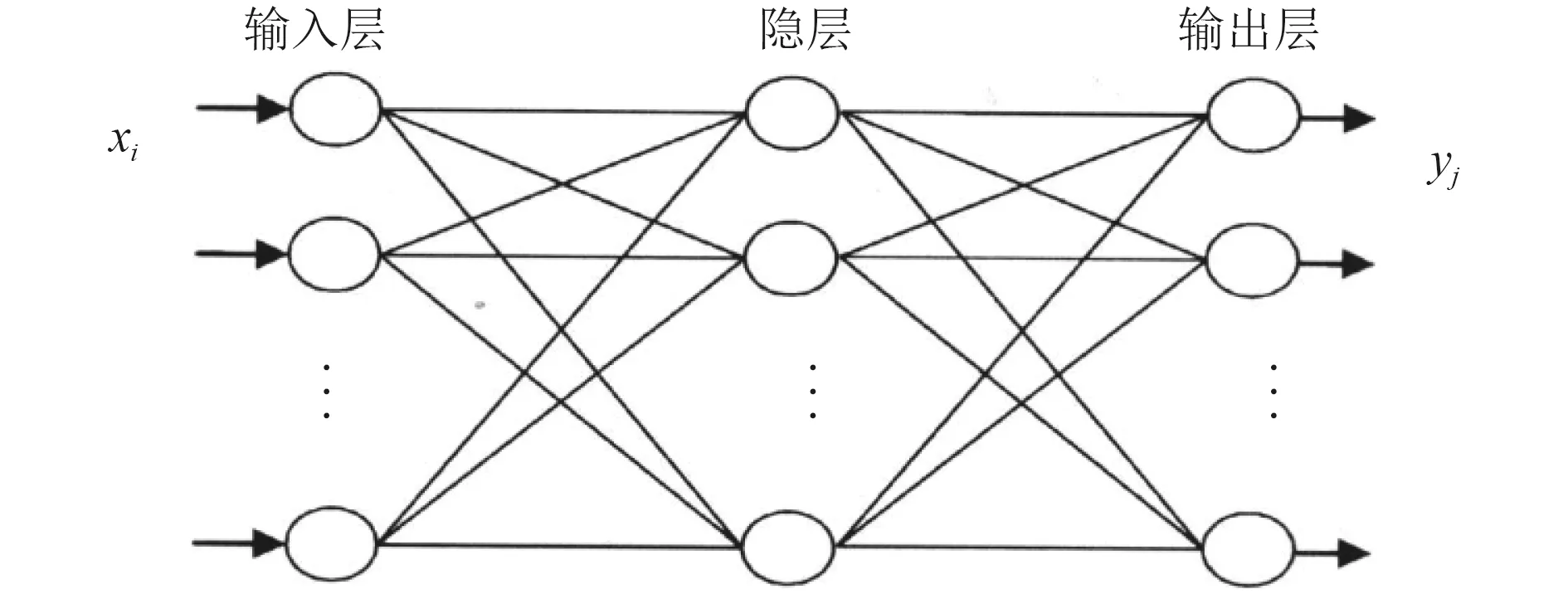
圖2 BP 神經網絡結構Fig. 2 Neural network structure

2.3 BP-GA 算法

BP 算法的實質是利用最陡下降法，具有簡單、計算量小、并行性強等優點，但它的學習過程收斂速度慢，容易陷入局部極小點，算法不完備，魯棒性不好，網絡性能差[14]。遺傳算法具有很強的魯棒性，能處理復雜的目標函數，避免收斂于局部最優，具有全局搜索能力，但同時遺傳算法通常的效率比其他傳統的優化方法低，遺傳算法容易過早收斂。由上面的分析可知BP 和GA 的優缺點間存在很大的互補性，所以本文提出BP-GA 算法[17]。

3 基于BP-GA 算法的環肋錐柱殼優化設計

3.1 優化策略以及流程

首先在Matlab 平臺上使用拉丁超立方體抽樣的方法生成600 個樣本點用于訓練神經網絡，其中50 個樣本點用于驗證神經網絡的精確度。然后利用有限元軟件Ansys 對環肋錐柱殼的強度和穩定性進行分析計算，得出相應的結構重量及總體失穩臨界壓力。采用BP 神經網絡分別建立起樣本點和結構重量之間、樣本點與失穩臨界壓力之間的映射關系，并對神經網絡進行訓練[18]。再調用一種基于NSGA-Ⅱ算法的多目標優化函數gamultiobj 進行全局尋優，得到Pareto 前沿。其中，fitnessfcn 為適應度函數，是通過目標函數與設計變量之間的函數關系式轉換的，而其函數關系式則是由前面的BP 神經網絡訓練得到。在本次優化中，利用BP 神經網絡建立起的設計變量與結構重量、總體失穩臨界壓力2 個目標函數之間的關系式分別為f1(x)和f2(x)，本文追求結構重量的最小值，總體失穩臨界壓力的最大值，因此適應度函數設為：fitness fcn1=f1(x)，fitness fcn2=1/f2(x)。整個優化流程如圖3 所示。

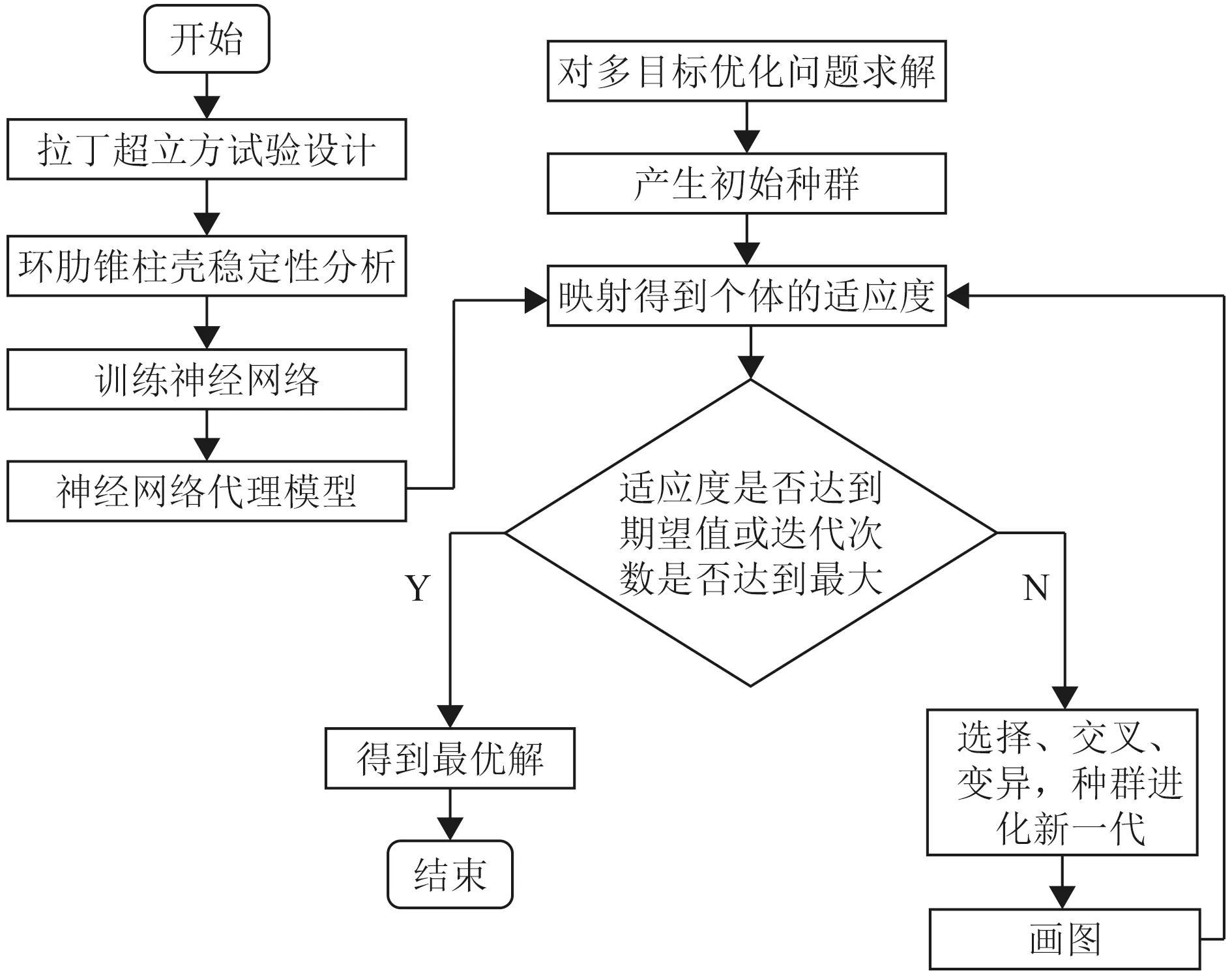
圖3 BP-GA 算法優化流程Fig. 3 Flow chart of BP-GA

3.2 建立模型

優化時采用的是1/2 耐壓殼簡化得到的環肋錐柱殼幾何模型，如圖4 所示。材料參數及其數據如下：耐壓殼厚度t=76 mm，錐柱結合處的耐壓殼會有應力集中問題，需要增厚處理，本文取1.5 倍的耐壓殼厚度，t0=114 mm；肋骨尺寸如上文h=416 mm，b=145 mm，t1=78 mm，肋骨間距lm=582 mm。用有限元軟件Ansys 進行建模，部分模型如圖5 所示，應力圖及1 階屈曲模態如圖6 所示。

根據艙段總體穩定性要求，P′cr≥1.2Pc，本文中，≥10.71 MPa。從圖6 的1 階屈曲模態可知臨界壓力系數為1.231 81，大于1.2，符合要求。當穩定性滿足要求時，應力遠遠小于臨界應力，所以優化時可以忽略強度要求。

圖6 環肋錐柱殼應力圖及1 階屈曲模態Fig. 6 Stress diagram and first-order buckling mode of ringstiffened cone-cylinder shell

3.3 優化的數學模型

環肋錐柱殼的目標函數為：

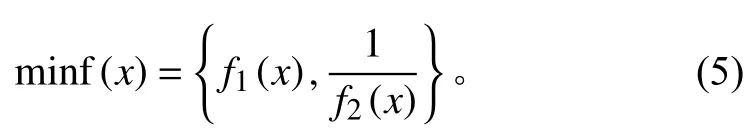
其中：f1(x)為 環肋錐柱殼的結構重量；f2(x)為總體失穩臨界壓力。

設計變量以及取值范圍如表5 所示，所有變量均為離散變量。其中，t為環肋錐柱殼殼體厚度。

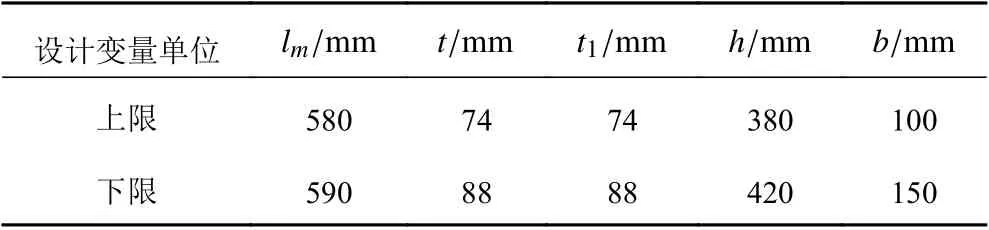
表5 設計變量及取值范圍Tab. 5 Design variables and range of values

4 結果分析與討論

為了衡量神經網絡代理模型的預測值和樣本值的差別采用平均相對變動值（Average Relative Variance，ARV）[19]，其定義為：

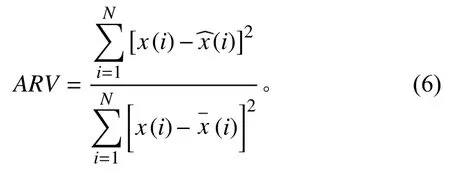
其中：N為驗證模型的樣本數量；x(i)為真實的響應值；(i) 為真實響應值的平均值；(i)為代理模型的預測值。可見，平均相對變動值ARV 越小，就表明神經網絡的預測效果越好。

為選取合適數目的樣本點進行神經網絡訓練，本文分別計算200 個、400 個、600 個這3 組樣本點的代理模型，從中選取50 個樣本點進行驗證，并計算平均相對變動值ARV。如表6 所示，當樣本點數目為200 時，結構重量的平均相對變動值為 6.37×10?6，已經十分接近0，隨著樣本點增多，ARV 值變化不大。然而失穩臨界壓力的預測精度就要差一些，需要增大樣本點數量以提高精確度。當樣本點取600 個時，失穩臨界壓力的ARV 值為 4.19×10?4，可以滿足要求。

表6 平均相對變動值ARVTab. 6 Average relative variance

600 個樣本點的BP 神經網絡訓練結果如圖7 和圖8 所示。可知，其結構重量預測的最大誤差絕對值不到3×10?3，總體臨界壓力誤差絕對值不足7×10?3，誤差均很小，說明神經網絡的映射精度較高。由此，可得到預測的結構重量與失穩臨界壓力，如圖9 和圖10所示。

通過多目標遺傳算法得到的Pareto 前沿如圖11 所示。Pareto 最優解即為可行域邊界最優前沿上的解，也是多目標問題的有效解。可以看到當改善結構重量時，帶來的必然是失穩壓力的損失，反之亦然。

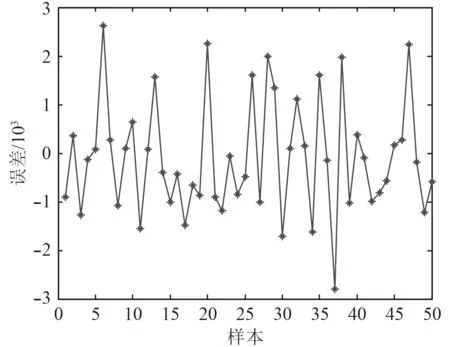
圖7 BP 網絡的結構重量預測誤差Fig. 7 BP network structural weight prediction error

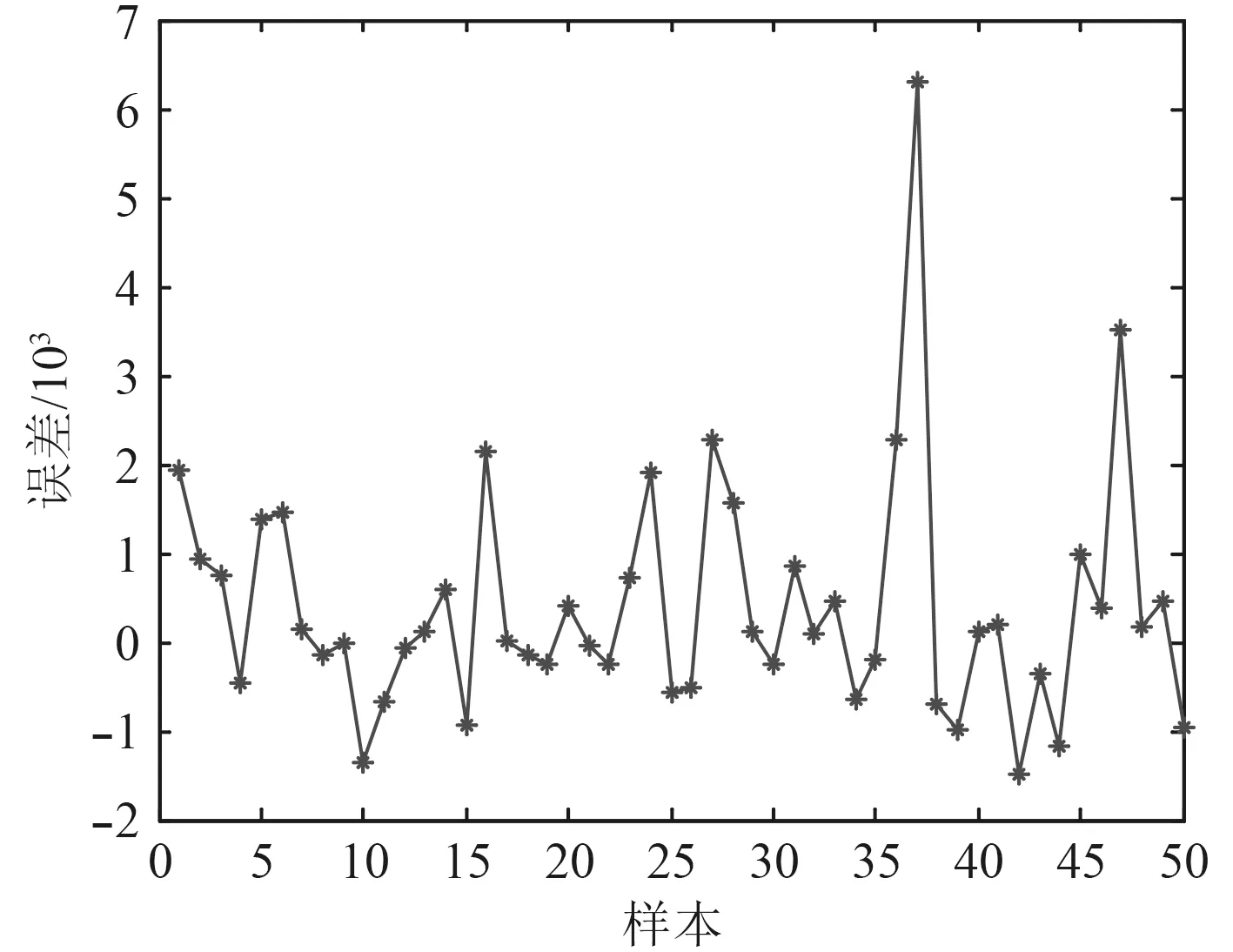
圖8 BP 網絡失穩臨界壓力預測誤差Fig. 8 BP network instability critical pressure prediction error

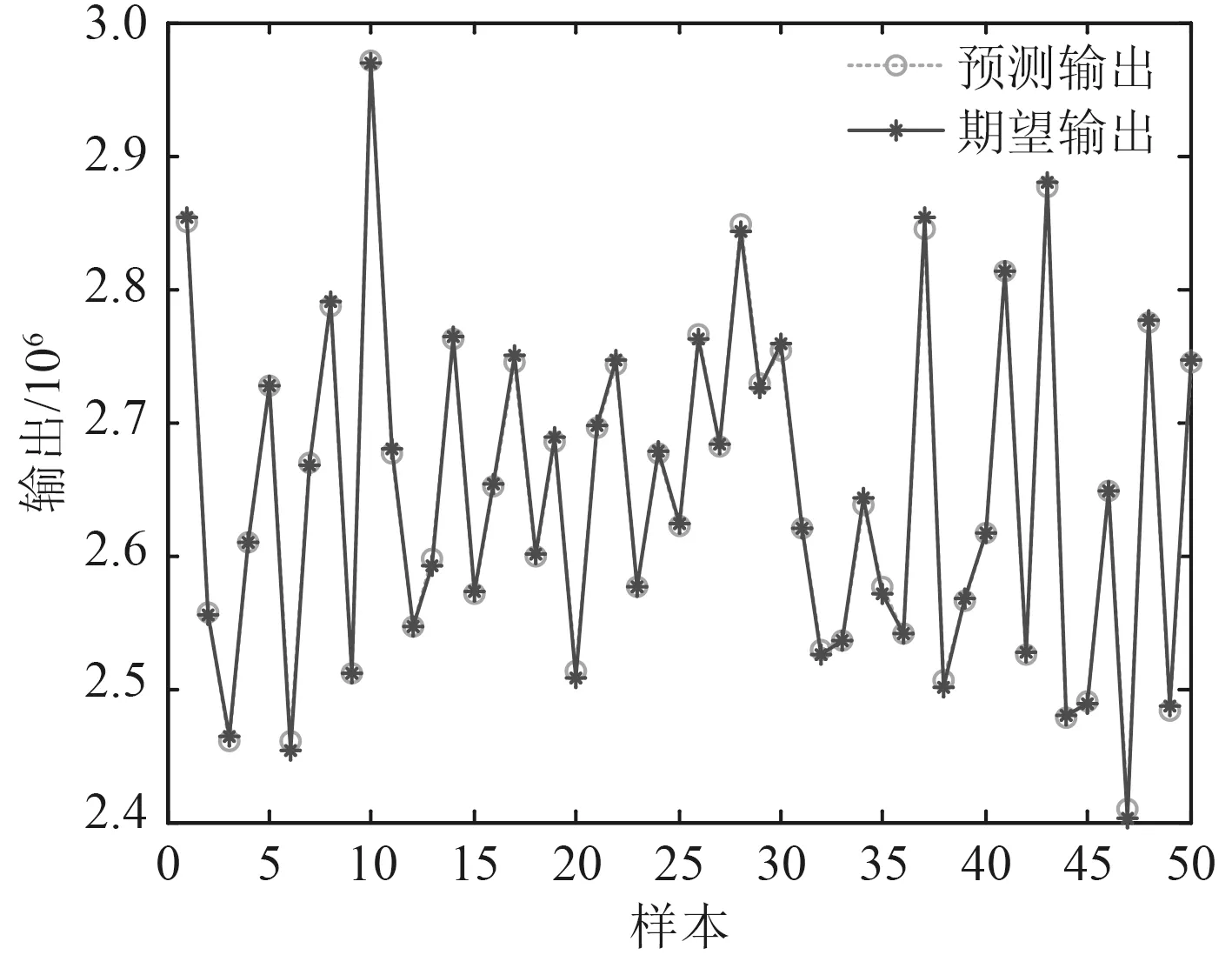
圖9 BP 網絡的結構重量預測輸出Fig. 9 BP network structure weight prediction output

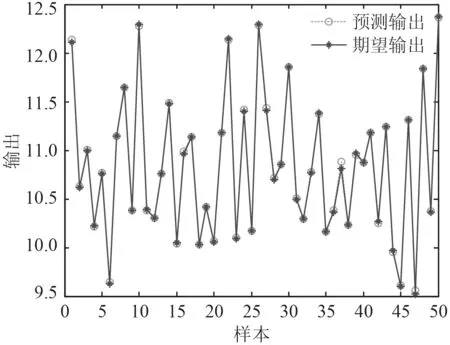
圖10 BP 網絡失穩臨界壓力預測輸出Fig. 10 BP network instability critical pressure prediction output

Pareto 前沿中共有300 組Pareto 最優解，表7 展示部分結果。

實際應用中，還需要從多個最優解中選取一個作為多目標優化的最終解，本文引用孫光勇[5]的最小距離選擇方法（TMDSM），從帕累托前沿中選取最優解。其原理為：D是從拐點到“烏托邦點”的距離，也就是TMDSM 中的最小距離，而拐點就是最優點，由此得到的優化結果如表8 所示。

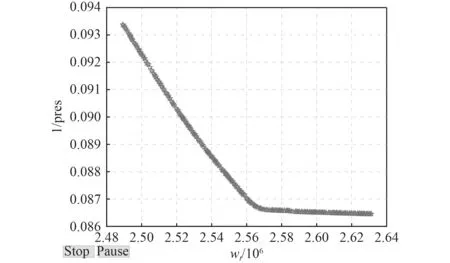
圖11 帕累托前沿Fig. 11 Pareto frontier

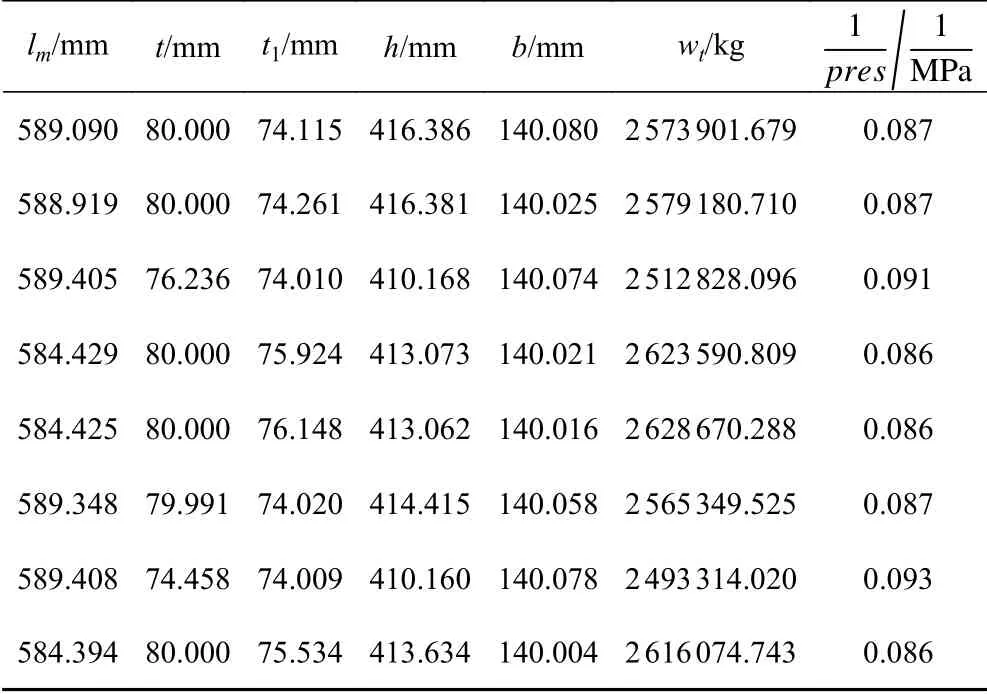
表7 部分帕累托最優解Tab. 7 Partial Pareto optimal solution

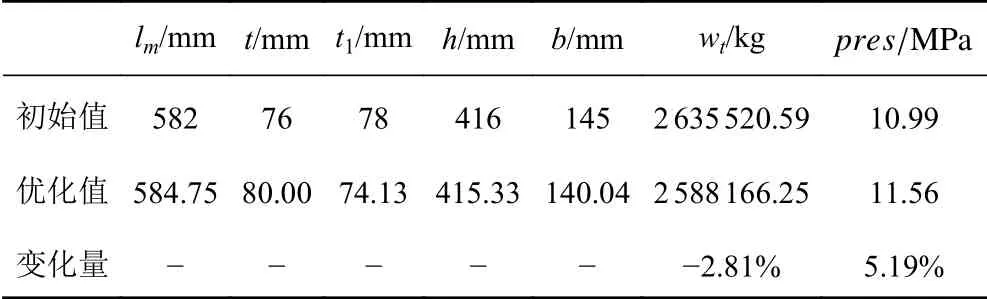
表8 優化結果Tab. 8 Optimization Results

從表8 可以看出，經過BP-GA 優化后，環肋錐柱殼的結構重量比初始時下降了2.81%，總體失穩臨界壓力也提高了5.19%，由于變量的初始選值與最終優化值相近，所以優化效果不突出，但仍得到了改善，說明優化合理。

由于上述優化結果是在BP 神經網絡建立起的映射關系的基礎上，利用遺傳算法進行優化搜索計算，最后需要將數據再代入有限元計算中，對BP 神經網絡映射的精度進行檢驗。如表9 所示，與最優解中的結果相比，環肋錐柱殼的結構重量誤差為 5.18×10?5，總體失穩臨界壓力誤差為?0.087%，誤差都較小，說明此次建立的BP 神經網絡具有較高的映射精度。

根據上文的計算結果wt=2 588.17 t，考慮首部球端，可以估算出耐壓殼的重量d1=2×1.02×wt=5 279.87 t，本文潛艇的最大排水量為D=16 000 t。根據《現代潛艇設計理論與技術》[20]中所述，現代柴電潛艇中結構重量占43%，攻擊型核潛艇中結構重量占45%。雙殼潛艇的外殼十分薄，本文取1/4 耐壓殼重量，再加上艙壁等結構，非耐壓殼結構重量約為1 500 t，故結構重量占最大排水量的42.4%<45%，所以潛艇自重滿足要求，上文的優化設計合理。

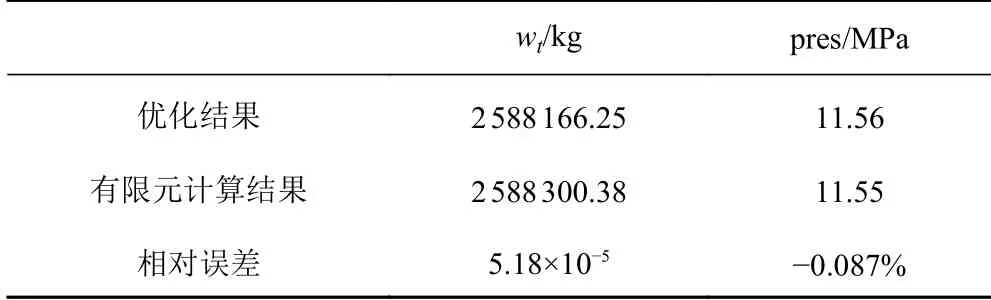
表9 有限元驗證Tab. 9 Finite element verification

5 結 語

本文基于多目標優化理論，依據重量排水量估算核潛艇主尺度，經過有限元計算校核結構重量、應力、失穩臨界壓力。以環肋錐柱殼的結構重量、總體失穩臨界壓力為目標，利用BP 神經網絡得到變量與優化目標之間的非線性映射關系，代替有限元方法計算的迭代方程式進行分析，然后利用遺傳算法進行優化設計，得到理想的優化結果，由此可知：

將神經網絡與遺傳算法相結合的方式解決復雜問題、大型計算的多目標優化計算，能達到互補優勢，不僅能克服神經網絡易陷入局部最優的劣勢，還能提高遺傳算法的計算效率，避免過早收斂的現象發生，并在環肋錐柱殼的優化問題中得到較好的效果。故該方法在潛艇耐壓殼上具有一定的價值，未來可以嘗試推廣至其他大型結構的優化設計上。