基于遺傳算法的電動舵機系統模糊PID控制

李璀璀，易文俊，管 軍，尹洪橋

(南京理工大學 瞬態物理國家重點實驗室， 南京 210094)

電動舵機作為終端執行機構，將指令信號迅速準確地轉化為舵偏角度[1]，直接決定了飛行控制系統的實際性能。

傳統的PID控制器參數固定，易于實現，廣泛應用于電動舵機控制系統中[2-3]。 然而，電動舵機系統是一個多變量、非線性時變的復雜系統[4]，傳統PID控制并不能滿足高精度的控制要求[5]。滑模控制具有廣泛適用，快速響應等優勢，但運行過程中存在難以消除的抖振，必須采取措施將其削弱至可容忍的范圍內[6-7]。內模控制在線調節參數少，跟蹤性能良好，但對于存在不確定性及非線性的復雜系統，這一方法受到一定限制[8]。分數階控制精度高[9]，但控制器結構復雜，整定參數較多。專家PID控制基于專家經驗[10]，原理簡單，但專家經驗不易于精確表述，控制系統部分信號量難以定量表示，在應用上存在局限。模糊PID控制基于模糊理論[11]，根據實際響應情況，通過模糊推理自動實現對PID參數的優化調整。模糊PID控制對于時變的復雜系統具有更好的適應能力，更符合電動舵機的控制要求。

模糊PID控制器的比例因子和量化因子對控制效果具有重要影響，而這些參數的確定大多依賴經驗，缺乏客觀性[12-13]，存在優化的空間。遺傳算法具有良好的全局優化能力和強大的并行計算能力[14-15]，適用于大規模復雜問題的優化。結合以上分析，提出利用遺傳算法同時優化模糊PID控制器的量化因子和比例因子，以獲取更優的控制效果。

1 遺傳算法優化的模糊PID電動舵機系統組成

1.1 電動舵機位置伺服系統模型

本文所研究的電動舵機以無刷直流電機作為伺服電機。假設無刷直流電機電樞導體連續均勻分布于電樞表面，不考慮磁滯損耗和渦流損耗，不計電樞反應，三相繞組對稱分布。舵機運動方程表示如下。

電樞回路電壓平衡方程[16]：

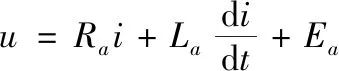
(1)

式中：u為電樞電壓(V)；Ra、La分別為電樞繞組的電阻(Ω)和電感(H)；i為電樞電流(A)。

反電動勢方程：

Ea=Keω

(2)

式中：Ea為反電動勢(V)；Ke為反電動勢常數(V·s/rad)；ω為電機轉速(rad/s)。

電磁轉矩方程：

Te=KTi

(3)

式中：Te為電樞電流產生的電磁轉矩(N·m)；KT為電機轉矩系數(N·m/A)。

轉矩平衡方程：

(4)

式中：TL為折算到電機軸上的負載轉矩(N·m)；J為折算到電機軸上的總轉動慣量(kg·m2)；Bv為系統等效粘滯摩擦系數(N·m/(rad·s-1))。

電動舵機模型如圖1所示。圖1中，N為減速比。負載為柔性負載，等效負載轉矩大小與舵機轉角成正比。在飛行過程中，電動舵機系統負載力矩不斷變化，故舵機模型是時變的。

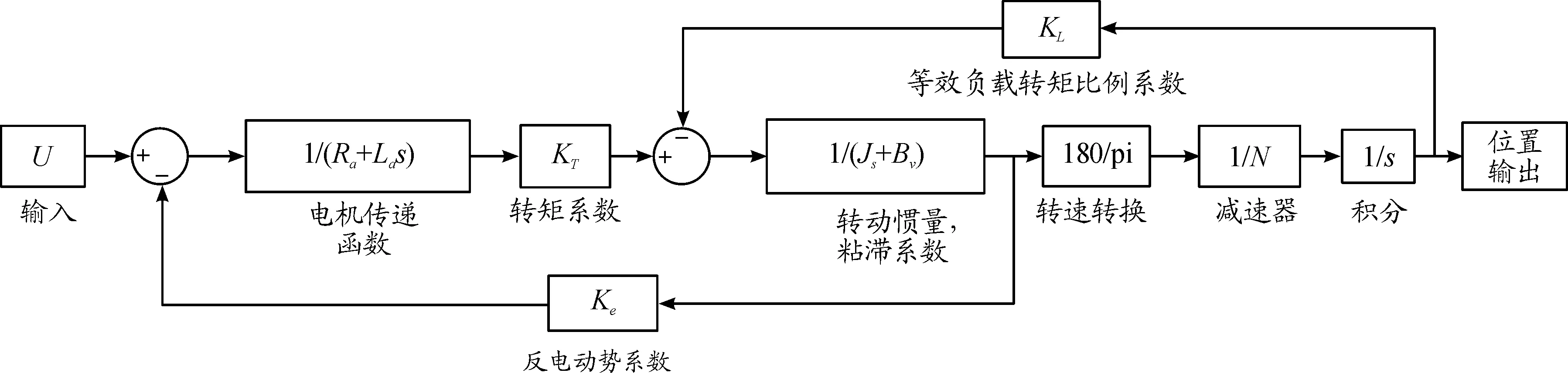
圖1 電動舵機模型框圖

電動舵機位置伺服控制系統采用三環控制，依次搭建電流環，轉速環和位置環。位置調節器采用融合智能算法的PID控制器，電流環和速度環均采用PI調節器，保證系統的穩態精度和動態跟蹤性能[17]。位置控制器和速度控制器均后置限幅環節和濾波環節。位置伺服控制系統模型如圖2所示。

圖2 電動舵機位置伺服系統模型框圖

1.2 模糊PID控制算法

模糊PID(Fuzzy PID，FPID)，亦稱模糊自整定PID，其綜合了模糊控制和PID控制的特點，具有結構簡單、自適應性強等優點。模糊PID控制器由模糊控制器和PID調節器兩部分組成。模糊控制器以誤差e作為輸入，經量化因子、模糊控制規則[18]、比例因子作用，輸出為PID參數的修正值ΔKp、ΔKi、ΔKd。其中，量化因子為Ke和Kec，ΔKp對應的比例因子為Kup，ΔKi對應的比例因子為Kui，ΔKd對應的比例因子為Kud。

找出PID 3個參數與e和ec之間的模糊關系，利用模糊控制原理在線對PID參數進行修改。模糊PID控制器結構如圖3所示。

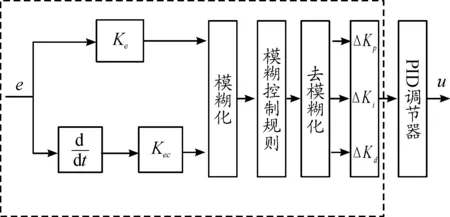
圖3 模糊PID控制器結構框圖

模糊整定PID控制器的表達式為：

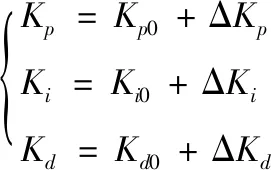
(5)

式(5)中，Kp0、Ki0、Kd0為經傳統經驗法整定出最優PID參數。

1.3 遺傳算法

遺傳算法(genetic algorithm，GA)是一類借鑒自然選擇和自然遺傳機制的隨機搜索算法。其模擬自然選擇和遺傳機制中的繁殖、交叉和基因突變現象，按照適應度函數并通過復制、交叉、變異3種遺傳算子對個體進行篩選。適應度高的個體被保留下來，組成新的種群。在若干代進化后，種群中個體適應度不斷提高，直至滿足給定條件。

2 遺傳算法優化的模糊PID控制器構建

模糊PID控制器參數的選取一般依賴于經驗，具有一定的局限性。考慮利用遺傳算法的全局優化能力和并行能力，同時優化模糊PID控制器的量化因子和比例因子，尋求以上參數的最優值。其主要步驟包括模糊PID控制器設計，參數編碼，適應度函數設計、復制、交叉和變異。設計出的基于遺傳算法的模糊PID(GAFPID) 控制器結構如圖4所示。

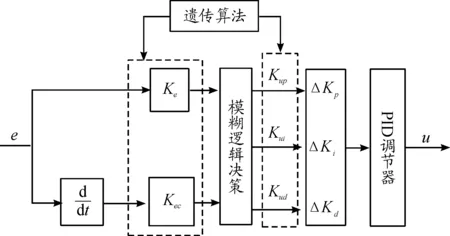
圖4 基于遺傳算法優化的模糊PID控制器結構框圖

2.1 模糊PID控制器設計

將模糊PID控制應用于電動舵機伺服系統位置環中，控制系統對位置信號的跟蹤。

2.1.1輸入變量和輸出變量

輸入變量設定為給定舵偏角與實際舵偏角之間的系統誤差e和系統誤差變化率ec，以PID控制器參數的3個修正值作為輸出變量。

系統誤差e的模糊論域取為[-3，3]，誤差變化率ec的模糊論域為[-3，3]，輸出變量ΔKp的模糊論域取為[-0.3，0.3]，ΔKi的模糊論域取為[-0.06，0.06]，ΔKd的模糊論域取為[-3，3]。

2.1.2隸屬度函數和模糊規則

設定輸入量和輸出量語言值的模糊子集為{負大，負中，負小，零，正小，正中，正大}，即{NB，NM，NS，ZO，PS，PM，PB}.隸屬度函數均選為Z形隸屬度函數(對應NB)，三角形隸屬度函數和S狀隸屬度函數(對應PB)。

綜合考慮系統的動態響應和穩態誤差要求，結合文獻[18]中模糊規則的選取，制定模糊控制規則表。以ΔKp為例，見表1。

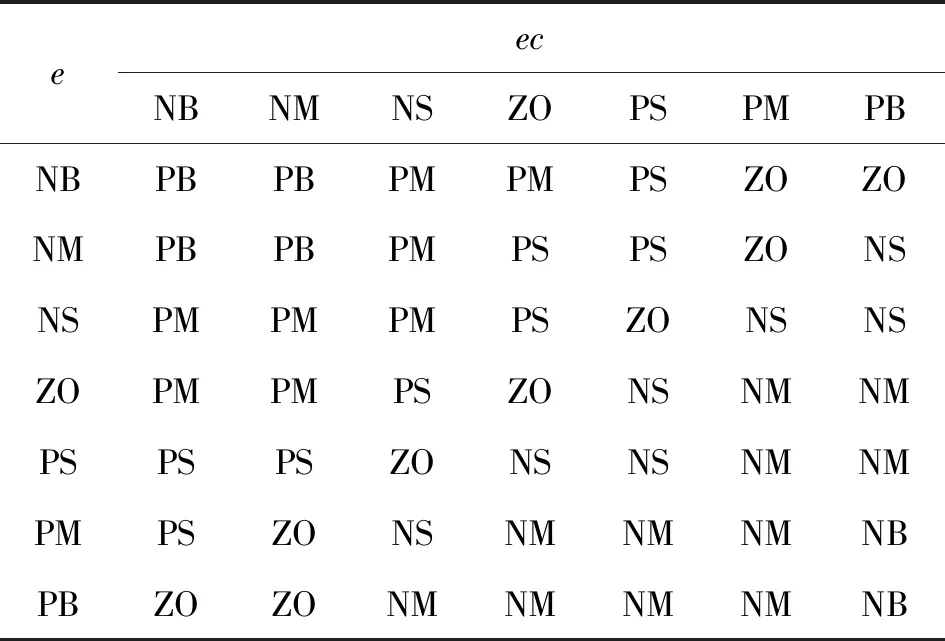
表1 ΔKp對應的模糊規則

2.1.3量化因子和比例因子

此時，控制器的性能主要取決于如下參數：量化因子Ke，Kec和比例因子Kup，Kui，Kud。在下面的階躍特性實驗中，由傳統經驗公式，計算出以上5個參數分別為0.5、3.2、2 000、50、0.003。在頻率特性實驗中，計算出的以上參數分別為0.25、150、3 300、40、0.003。量化因子和比例因子的引入，實現了變量在基本論域與模糊論域及模糊論域與基本論域之間的相互轉換，很大程度上影響了控制效果。

2.2 編碼

考慮到實數編碼可操作性強，易通過編程實現，故選用實數編碼，將模糊控制器中的量化因子和比例因子作為個體中的基因。通過對以上參數的尋優，改善原有模糊控制器的性能。

2.3 適應度函數

適應度反映了遺傳算法優化過程中個體接近群體最優值的優良程度，直接影響遺傳算法的性能。遺傳算法優化模糊控制器目的是參數尋優后，系統的性能指標J最小。性能指標越小，適應度越大。因此，適應度函數可取為F=1/J。

為獲取滿意的過渡過程動態特性，采用誤差絕對值時間積分性能指標作為參數選擇的目標函數。參數選取的最優指標為：

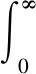
(6)

式(6)中，e(t)為系統誤差。為防止控制能量過大，在仿真過程中加入了控制器輸出限幅環節。

2.4 復制

復制是從一個舊種群中選擇生命力強的個體位串產生新種群的過程。由于基本上每個個體適應度均不同，故可采用一種適應度比例法進行選擇，即種群中每個個體被選擇的可能性與其適應度成正比。即：

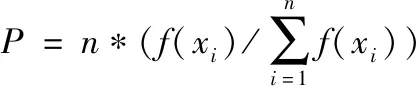
(7)

式(7)中：n為種群中個體數；f(xi)是種群中第i個個體的適應度；P記為第i個個體被選中的可能性，為一實數。

結合精英保留策略，保留各代中選中可能性大于1的個體，并根據適應度大小對上述個體進行復制，產生比初始種群優秀的新種群。種群中個體適應度按順序遞增。

2.5 交叉和變異

交叉概率Pc較大時，重組個體出現的概率大，同時新舊個體替換過快，可能會使部分表現較好的個體被過早淘汰。變異概率Pm較大時，尋優空間可能過大，收斂時間延長。

基本遺傳算法中交叉概率和變異概率為定值，在具體實驗中存在一定局限性。采用一種自適應的交叉概率和變異概率，表達式為：

(8)

式(8)中：Pc max是最大交叉概率；ΔPc是交叉概率改變量，為一定值；Pm max是最大變異概率；ΔPm是變異概率改變量，為一定值；n是種群中的個體數目。

交叉概率和變異概率隨個體適應度值的變化而變化，適應度值越大，交叉概率和變異概率越小。其中，交叉操作在相鄰2個個體間按概率進行。根據實際情況，選取下面的參數，最大交叉概率取為0.9，交叉概率改變量取為0.2，最大變異概率取為0.1，變異概率改變量取為0.06，種群中個體數目取為50。

2.6 基于遺傳算法的電動舵機系統模糊PID控制

遺傳算法優化電動舵機模糊PID伺服控制系統流程如圖5所示。

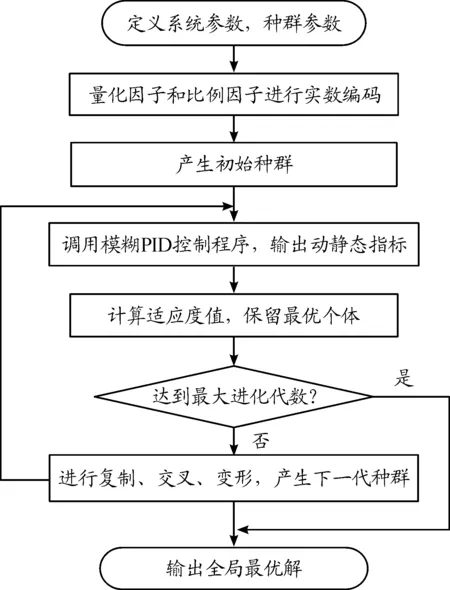
圖5 基于遺傳算法的電動舵機系統模糊PID控制流程框圖

3 仿真實驗及分析

在Matlab環境下，根據電動舵機伺服控制系統結構和上述控制律，結合工程整定法，對電動舵機位置控制進行仿真。比較模糊PID(FPID)控制策略和遺傳算法優化的模糊PID(GAFPID)控制策略對舵機伺服系統位置信號跟蹤的控制效果，驗證本文設計的控制策略的優越性。

電動舵機系統的具體參數為：折算到電機軸上的總轉動慣量為5×10-5kg· m2，等效負載轉矩比例系數為0.02 N·m/(°)，電樞電感為0.056 5 mH，電樞電阻為0.143 Ω，轉矩系數為0.026 3 N·m/A，反電動勢系數為2.754 1×10-3V/rpm，電機選用的是MAXON公司某型號直流無刷電機，其額定電壓為24 V，額定轉矩為311 mN·m。

遺傳算法中，種群大小取為50，最大交叉概率取為0.9，最大變異概率取為0.1。階躍響應下響應時間取為0.06 s，頻率響應下響應時間取為0.2 s。最大進化代數取為100代。

3.1 系統指標

電動舵機伺服控制系統指標如下：1) 最大輸出角度為12°；2) 最大響應頻率10 Hz；3) 最大負載力矩2.4 N·m(12°)；4) 穩態最大幅值誤差≤0.1°；5) 穩態最大相位誤差≤10°。

3.2 仿真結果及分析

將正弦信號和階躍信號作為給定的位置信號，在帶載條件下進行仿真。負載為柔性負載，等效負載轉矩大小與舵機轉角成正比。舵機轉角與等效負載轉矩比例系數的乘積即為折算到電機軸上的負載轉矩。

3.2.1階躍特性仿真結果

帶載條件下，輸入指令為12°階躍信號。分別將傳統PID控制律、模糊PID控制律、遺傳算法優化的模糊PID控制律應用于舵機伺服系統的位置環，采樣時間設為0.1 ms，記錄系統的動靜態指標。仿真結果如圖6、圖7和表2所示。

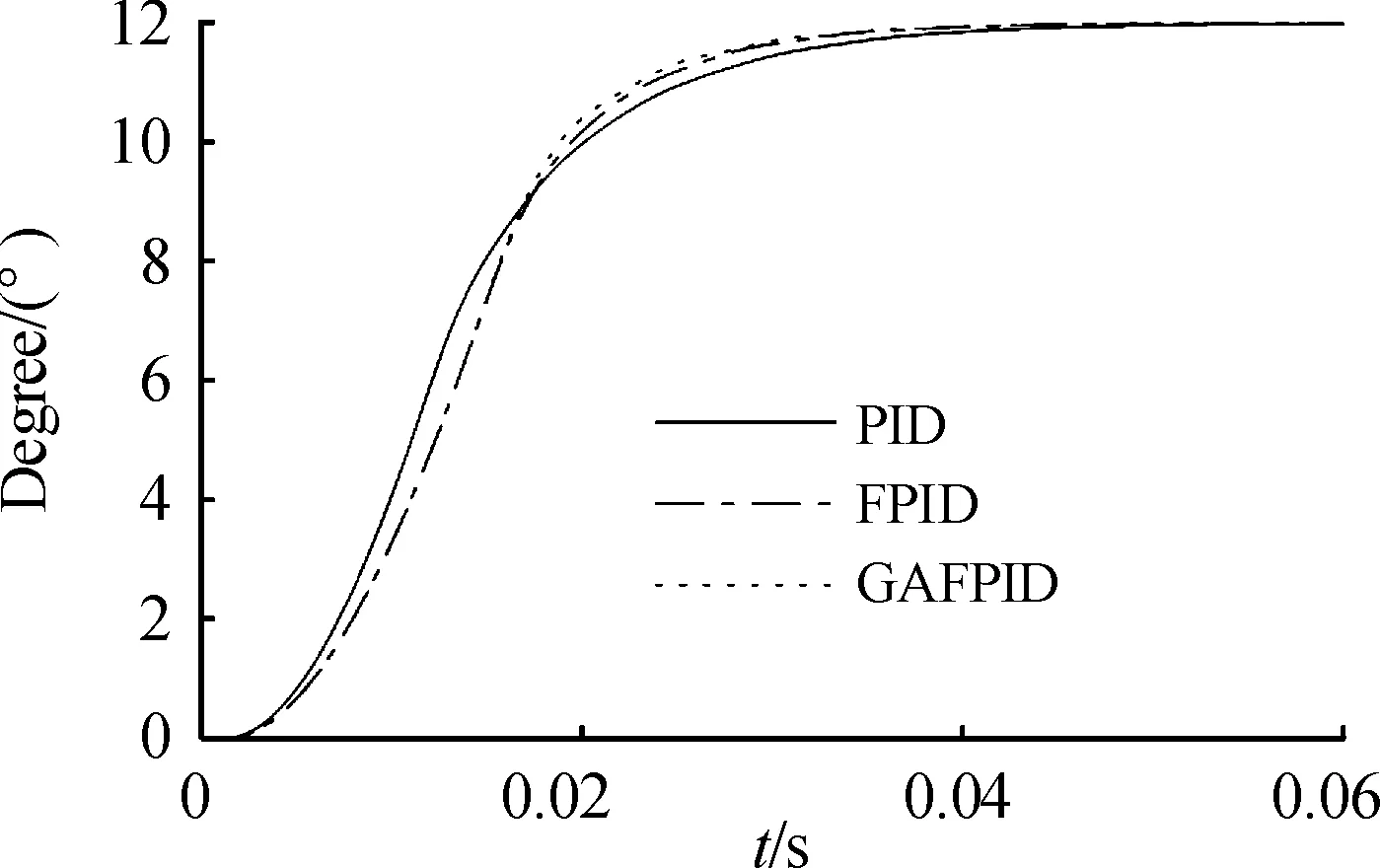
圖6 系統帶載階躍響應圖

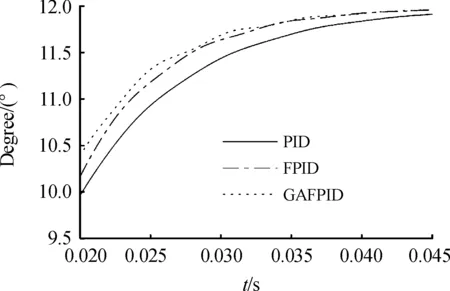
圖7 系統帶載階躍響應局部放大圖

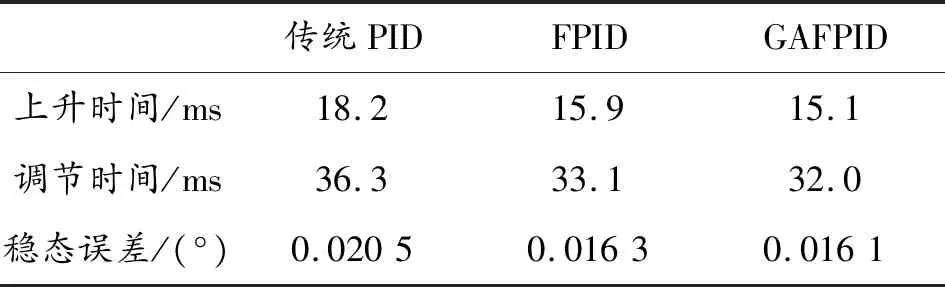
表2 負載階躍響應仿真數據

由圖6、圖7和表2可知，在帶載階躍響應下，遺傳算法優化的模糊PID控制器控制下系統的上升時間比經典PID控制縮短了約17.03%，比模糊PID控制縮短了約5.03%。在帶載階躍響應下，遺傳算法優化的模糊PID控制器控制下系統的調節時間比經典PID控制縮短了約11.84%，比模糊PID控制縮短了約3.32%。在穩態響應上，模糊PID控制律和遺傳算法優化的模糊PID控制律下系統穩態誤差少于傳統PID控制律下的系統。遺傳模糊PID控制下系統的穩態誤差較經典PID控制減少了21.46%，較模糊PID控制減少了1.22%。

3.2.2頻率特性仿真結果

帶載條件下，輸入指令為10 Hz，12°的正弦信號。分別將傳統PID控制律、模糊PID控制律、遺傳算法優化的模糊PID控制律應用于舵機伺服系統的位置環，采樣時間設為0.1ms，記錄穩定狀態下系統的最大幅值誤差和最大相位誤差。仿真結果如圖8、圖9和表3所示。

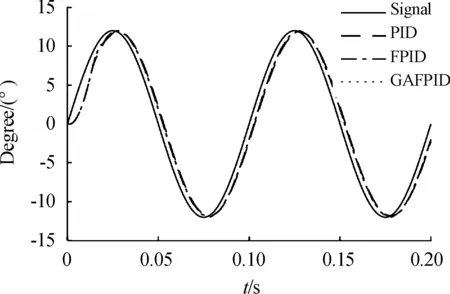
圖8 系統帶載10 Hz正弦信號跟蹤響應圖

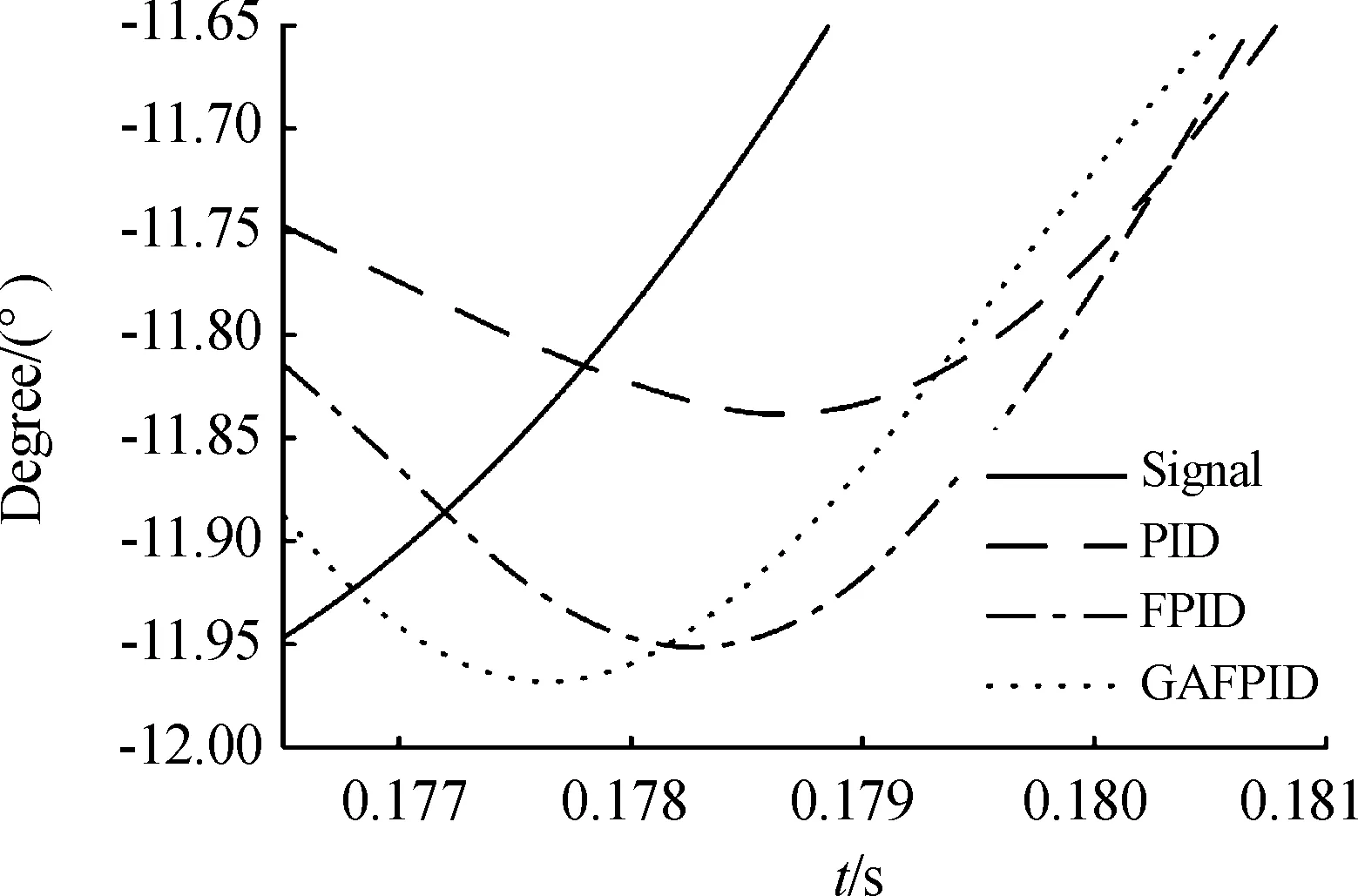
圖9 系統帶載10 Hz正弦信號跟蹤響應局部放大圖

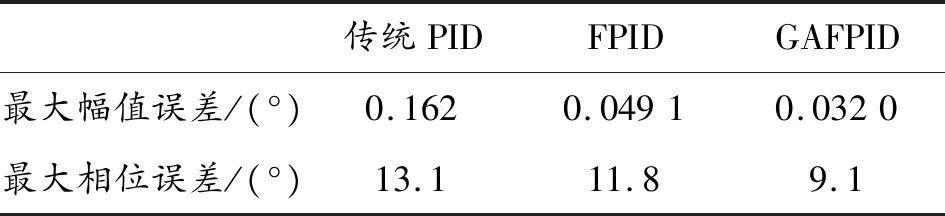
表3 負載頻率響應仿真數據

由圖8、圖9和表3可知，帶載情況下，輸入信號為10 Hz、12°的正弦信號時，傳統PID控制下穩態系統最大相位誤差和幅值誤差均超過了允許值，其已不能勝任對給定的正弦信號的跟蹤。在最大幅值誤差方面，模糊PID控制和遺傳算法優化的模糊PID控制均滿足系統要求，其中遺傳模糊PID控制下的系統較模糊PID控制系統減少了34.82%。在最大相位誤差方面，模糊PID控制不能滿足系統要求，而遺傳算法優化的模糊PID控制律下的系統較模糊PID降低了22.88%，能夠滿足指標要求。

4 結論

本文設計了一種自適應遺傳算法應用于電動舵機系統位置環模糊控制中。該方法對位置環模糊PID控制器的量化因子和比例因子進行尋優。分別將傳統PID控制器、模糊PID控制器和遺傳算法優化的模糊PID控制器應用于電動舵機系統的位置環中進行仿真。仿真結果表明，基于遺傳算法的模糊PID控制下的舵機系統階躍響應上升時間15.1 ms，調節時間32.0 ms，穩態誤差為0.016 1°，頻率特性穩態最大幅值誤差0.032 0°，穩態最大相位誤差9.1°，在動態響應特性和穩態精度上有了明顯提升。