舵翼結構模型氣動熱力耦合關系仿真研究

張佳明，王文瑞，馬新杰，溫曉東

(1.北京科技大學 機械工程學院， 北京 100083; 2.流體與材料相互作用教育部重點實驗室， 北京 100083;3.天津航天機電設備研究所 天津市宇航智能裝備技術企業重點實驗室， 天津 300301)

近空間飛行器擁有快速響應、突防能力強等特點，能夠在短時間內精準打擊長距離軍事目標，在國防科研、空間技術研究中具有極其重要的戰略意義[1-2]。飛行器在高馬赫數飛行過程中，周圍空氣受到激波的強烈壓縮，對飛行器表面產生劇烈的氣動熱力載荷。舵翼結構作為飛行器關鍵部件，為了確保燃料供給能夠滿足高速、長距離飛行，要求盡量減小結構尺寸，結構剛度的降低導致更大的變形量，影響其氣動外形，進一步增強氣動熱、氣動力與結構響應之間的耦合效應[3-5]，直接影響飛行穩定性，嚴重時造成偏離飛行軌道甚至掉落，影響精確打擊效果，這也是目前近空間飛行器熱防護設計與結構設計過程中必然要面對的問題。

為此，多位研究者開展了相關的試驗項目。夏吝時等[6]對主動式熱疏導簡化前緣金屬開展地面熱環境模擬試驗。吳大方等[7-8]對近空間飛行器復合材料先后開展了1 100 ℃和1 500 ℃的熱振聯合實驗。蔡禮港、歐朝、李強等[9-11]在電弧風洞、激波風洞中對飛行器結構與熱防護材料開展了實驗研究。然而，開展試驗周期長、難度大、費用高，使用數值仿真方法對近空間飛行器結構溫度、變形進行預測，能夠更為高效地為熱防護設計與結構設計提供指導。李佳偉等[12]采用一體化求解方法，將流場與結構溫度場作為一個物理場，采用統一的控制方程進行求解，避開了傳統耦合方法在迭代計算時場之間的大量數據交換。季衛棟等[13]采用統一的積分方程組作為氣動加熱和結構熱物理過程的控制方程，對物理場進行統一的迎風格式有限體積方法離散，對二維圓管模型的氣動加熱和結構傳熱問題進行了模擬。陳梅潔等[14]通過順序耦合方法，基于Transitionk-k1-ω湍流模型計算得到了溫度場和應力場的分布。梁杰等[15]采用蒙特卡洛方法，通過分區求解策略對大型航天器離軌再入隕落過程中的氣動力和氣動熱特性進行了數值模擬。

當前研究者更多關注于多物理場耦合方法的實現，而在實現仿真的基礎上，開展各物理場之間的耦合關系分析，對于熱防護材料設計及其結構設計有著更為現實的意義[16]。為此，本文通過分區耦合方法，開展舵翼結構流-熱-固耦合仿真，對不同飛行迎角狀態下結構變形場、溫度場進行計算，實現氣動力、氣動熱及結構耦合響應的量化分析。

1 多場耦合理論

1.1 數值計算理論

流-熱-固多場耦合根據以下6個方程進行數值計算。

1) 質量守恒方程。

(1)

式(1)中：▽代表拉普拉斯算子；V為速度矢量(u、v、w)，指流體微元在x、y、z等3個方向的速度分量(m/s)；ρf為流體密度(kg/m3)；t為時間(s)。

2) 動量守恒方程。

(2)

3) 能量守恒方程。

(3)

式(3)中：E為總能量(J)；ρ為材料密度(kg/m3)；fw=fxu+fyv+fzw為單位質量的流體體積力所做的功(J)。

4) 氣體狀態方程。

p=Z(R*/M)ρfT

(4)

式(4)中：M表示氣體摩爾質量(kg/mol)；R*為摩爾氣體常數，R*=8.314 5 J/(mol·K)；T為溫度場(K)；Z為壓縮因子。

5) 傳熱方程。

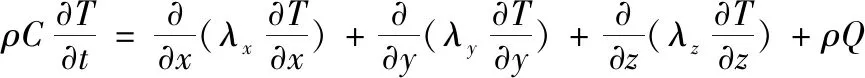
(5)

式(5)中：λ為材料的導熱系數(W/(m·K))；C為比熱容(J/kg·K)；Q為物體內部的熱源強度(W/kg)。

6) 結構響應方程。

[σ]=[D][ε]

(6)

式(6)中，[σ]為應力矩陣；[D]為結構材料彈性矩陣；[ε]為結構的總應變矩陣。

1.2 多物理場耦合方法

舵翼結構在近空間環境中飛行時，氣動加熱過程是一個持續的、非穩態的過程，并且是流場、溫度場和結構場相互耦合作用的過程，因此采用流-熱-固耦合方法進行多物理場耦合問題的求解。熱流固耦合模型如圖1所示，在流體域內使用基于有限體積法的Fluent求解器，對流場的熱流和壓力進行求解，使用System Coupling模塊，通過流固耦合界面將熱載與氣動力載荷傳遞至固體域。在固體域內使用Transient Structural求解器，對固體域的溫度與變形進行求解，使用System Coupling模塊通過流固耦合界面將溫度場與變形場傳遞至流體域，繼續進行流體域的下一步計算，直到達到設置的耦合計算時間。

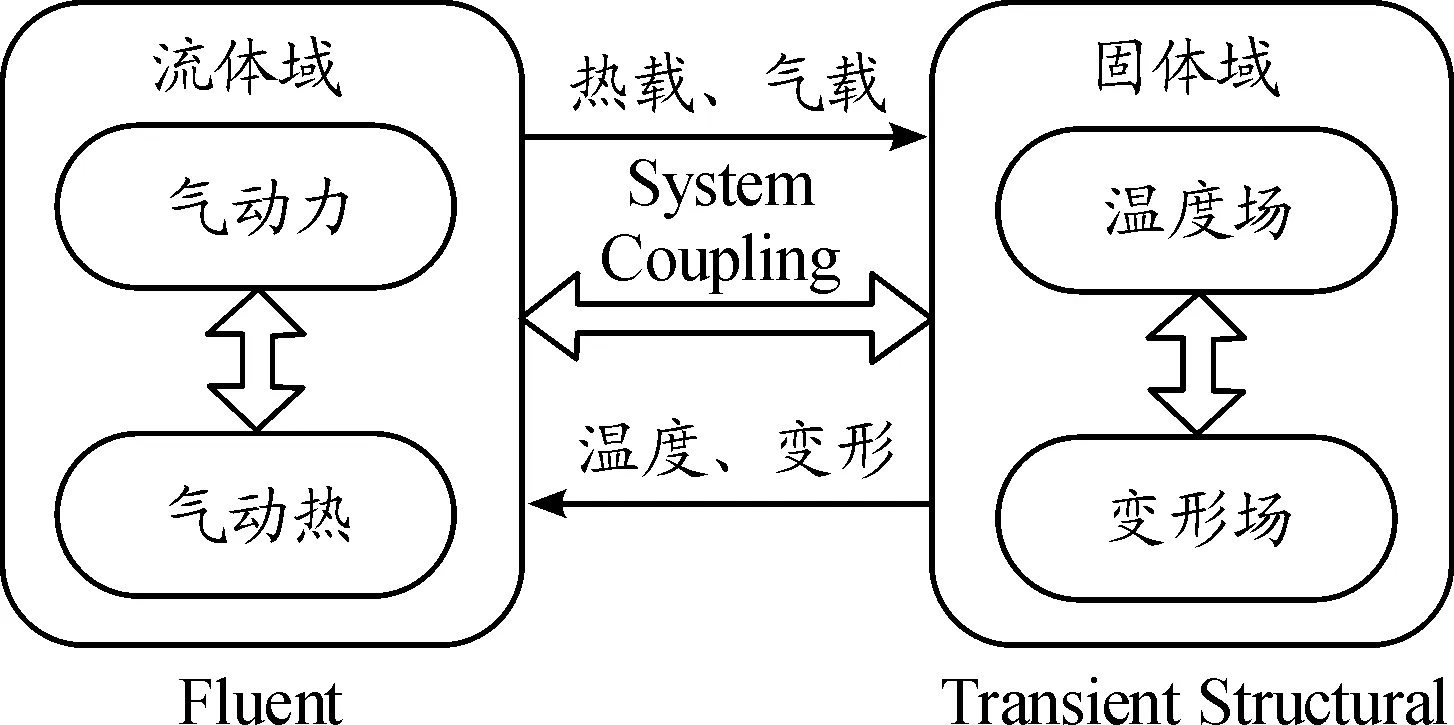
圖1 熱流固耦合模型示意圖

2 仿真算法校驗

為驗證本文選用多物理場耦合算法的準確性，利用經典的圓管繞流試驗作為驗證算例。該試驗是1987年美國科學家 Allan R.Wieting在NASA LANGLEY 8-foot高溫風洞中進行的，試驗如圖2所示。

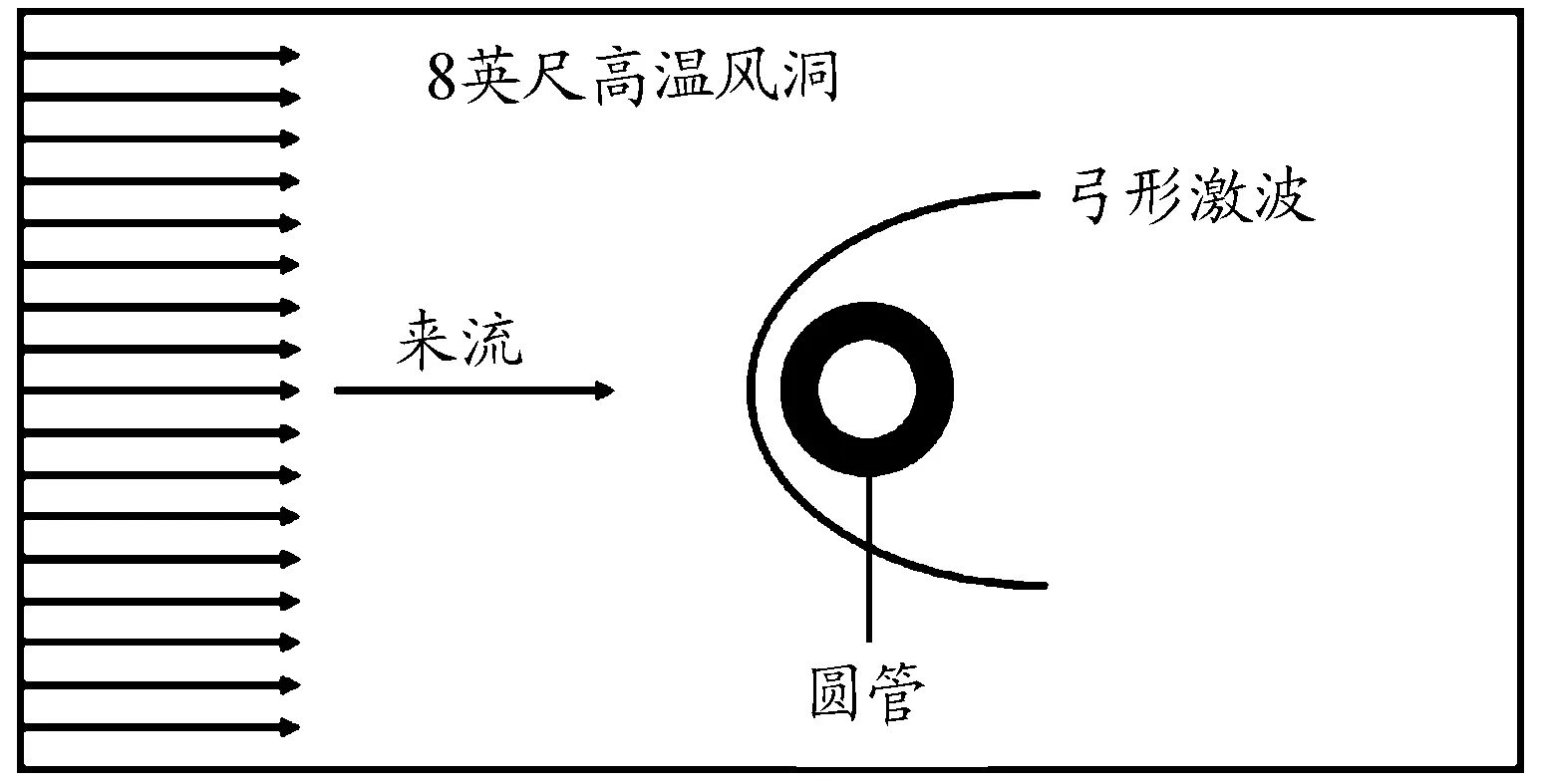
圖2 圓管繞流風洞試驗示意圖

風洞試驗中，不銹鋼圓管是完全對稱的圓柱體，因此本文中采用1/2模型進行計算，以提高計算效率。利用SolidWorks軟件建立流場及圓柱模型，采用結構化網格，在邊界層處和激波位置處進行網格加密處理。流體域和固體域在耦合面上網格節點是連續的，保證流固耦合面上的幾何相容性，模型網格如圖3所示。流體域網格數量為22 866，固體域網格數量為3 249，網格質量均大于0.985。流體域入口、出口設置為遠場邊界條件，流場參數設置如表1所示，耦合面按流固耦合邊界條件設置。圓管內徑為25.4 mm，外徑為38.1 mm，材料為1Cr18Ni9Ti不銹鋼，材料參數如表2所示，圓管初始溫度為294.4 K。

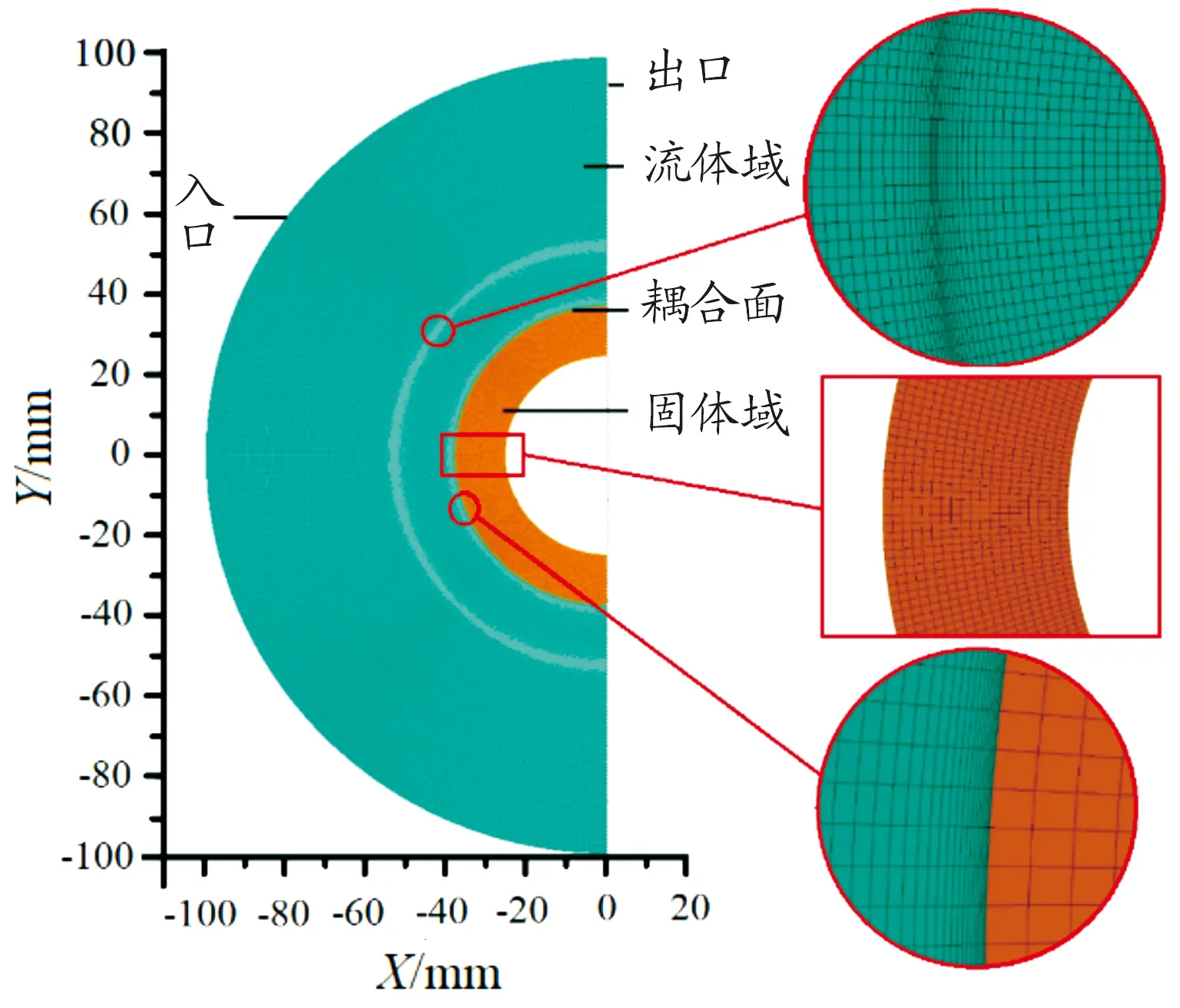
圖3 網格邊界條件示意圖

表1 來流參數

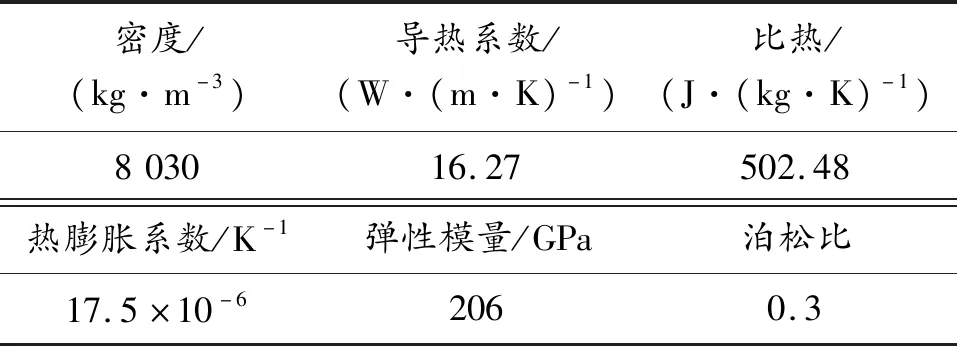
表2 不銹鋼材料參數

仿真耦合求解時間設置為2s，與文獻[17]相同。圖4為仿真流場溫度分布云圖與文獻試驗激波紋影，二者形狀相吻合。圖5表示了仿真結果與文獻中的流場溫度突變位置、流場溫度，二者分別相差0.071%與2.369%。圖6表示了仿真結果與文獻中的圓管結構溫度分布、應力分布，二者分別相差0.345%和0.567%，具體數據如表3所示。由上述分析可知，仿真結果與文獻所述基本吻合，說明本文所使用的多場耦合方法是準確有效的。

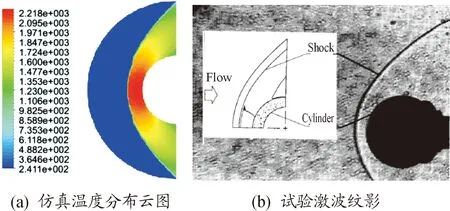
圖4 外流場參數分布圖

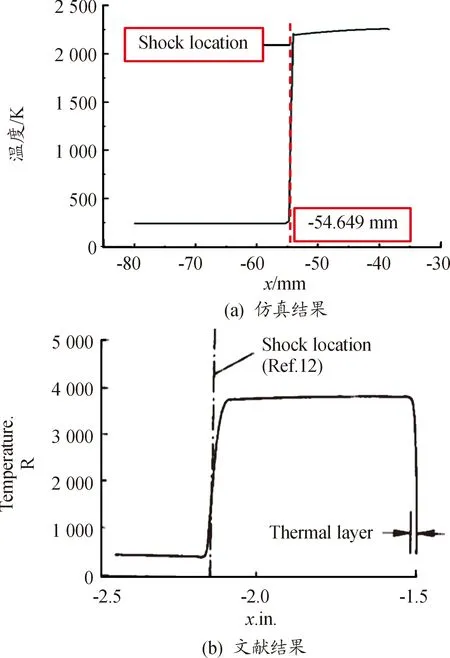
圖5 駐點徑向流場參數曲線

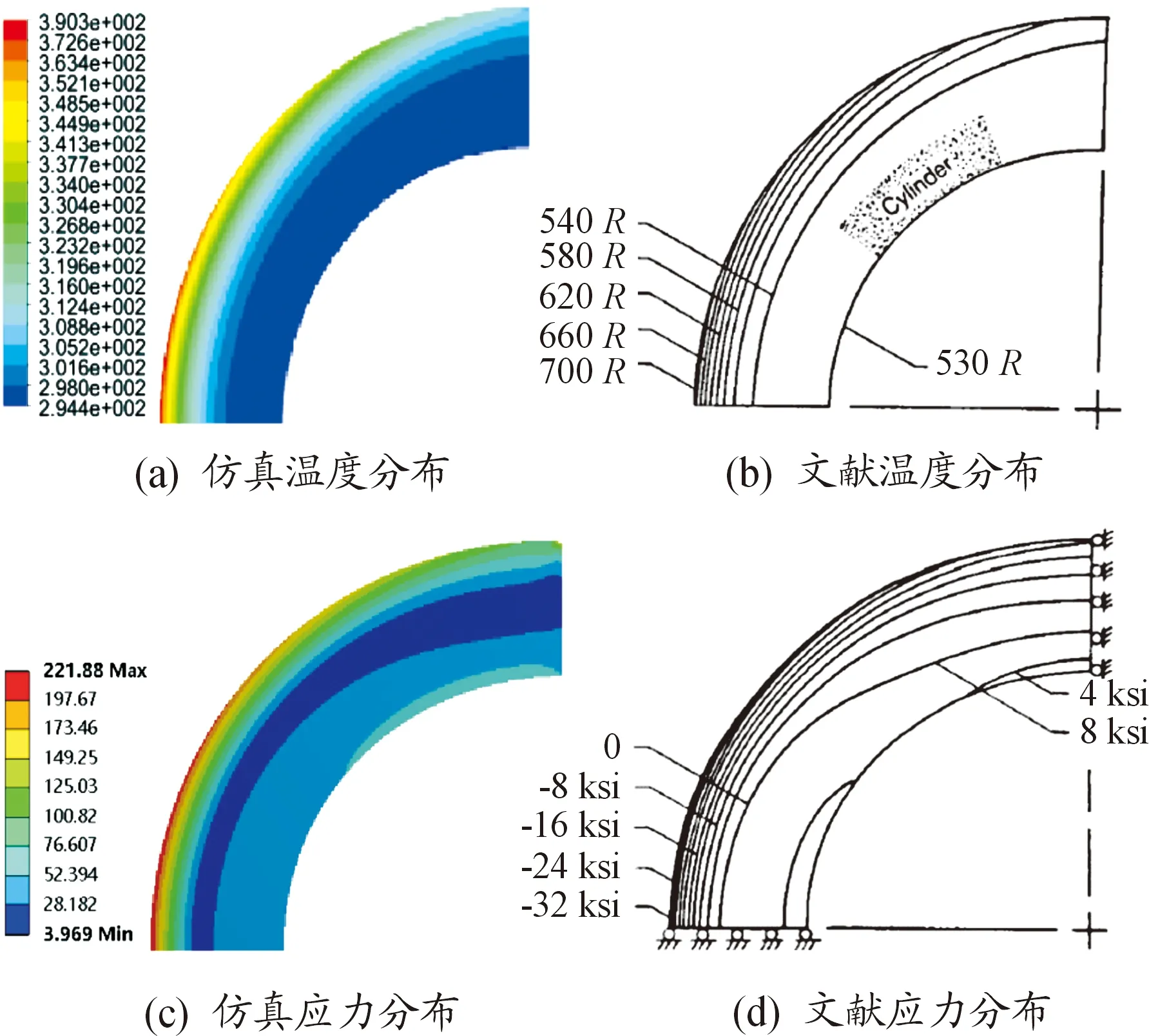
圖6 圓管結構溫度與應力分布圖

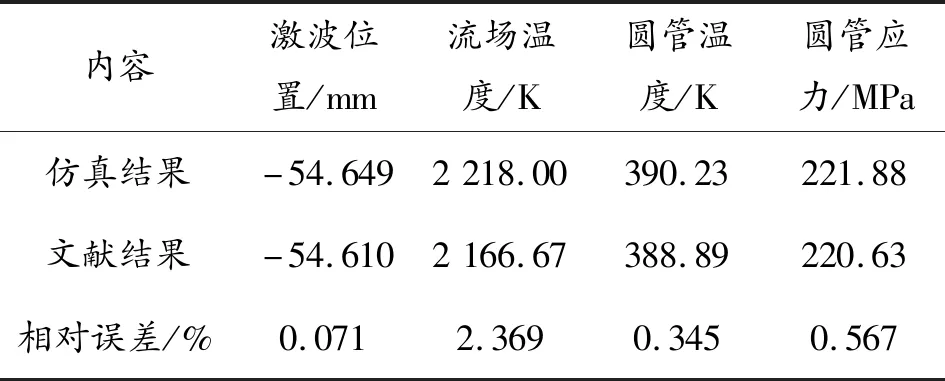
表3 仿真與文獻數據對比

3 舵翼結構模型耦合計算結果與分析

3.1 有限元建模

舵翼結構尺寸如圖7(a)所示，材料為D6AC高溫合金鋼，材料參數如表4所示，計算模型流體域、固體域網格分別如圖7(b)、圖7(c)所示。模型計算域的邊界條件如圖7(d)所示，壁面邊界選擇無滑移邊界條件，將初始壁溫設置為216.65 K，流體域外邊界設置為壓力遠場邊界條件，模擬飛行高度為20 km，來流速度5Ma，壓強5 529.3 Pa，溫度216.65 K，密度0.088 91 kg/m3。固體結構場設置為彈性結構，尾部施加固定約束，對稱面添加對稱約束，將舵翼結構與外流場交界面設置為流-固耦合面，在界面上進行分區耦合之間的數據傳輸。根據舵翼結構飛行特點，設置飛行迎角為-10°、-5°、0°、5°、10°進行計算，耦合時間為40 s。

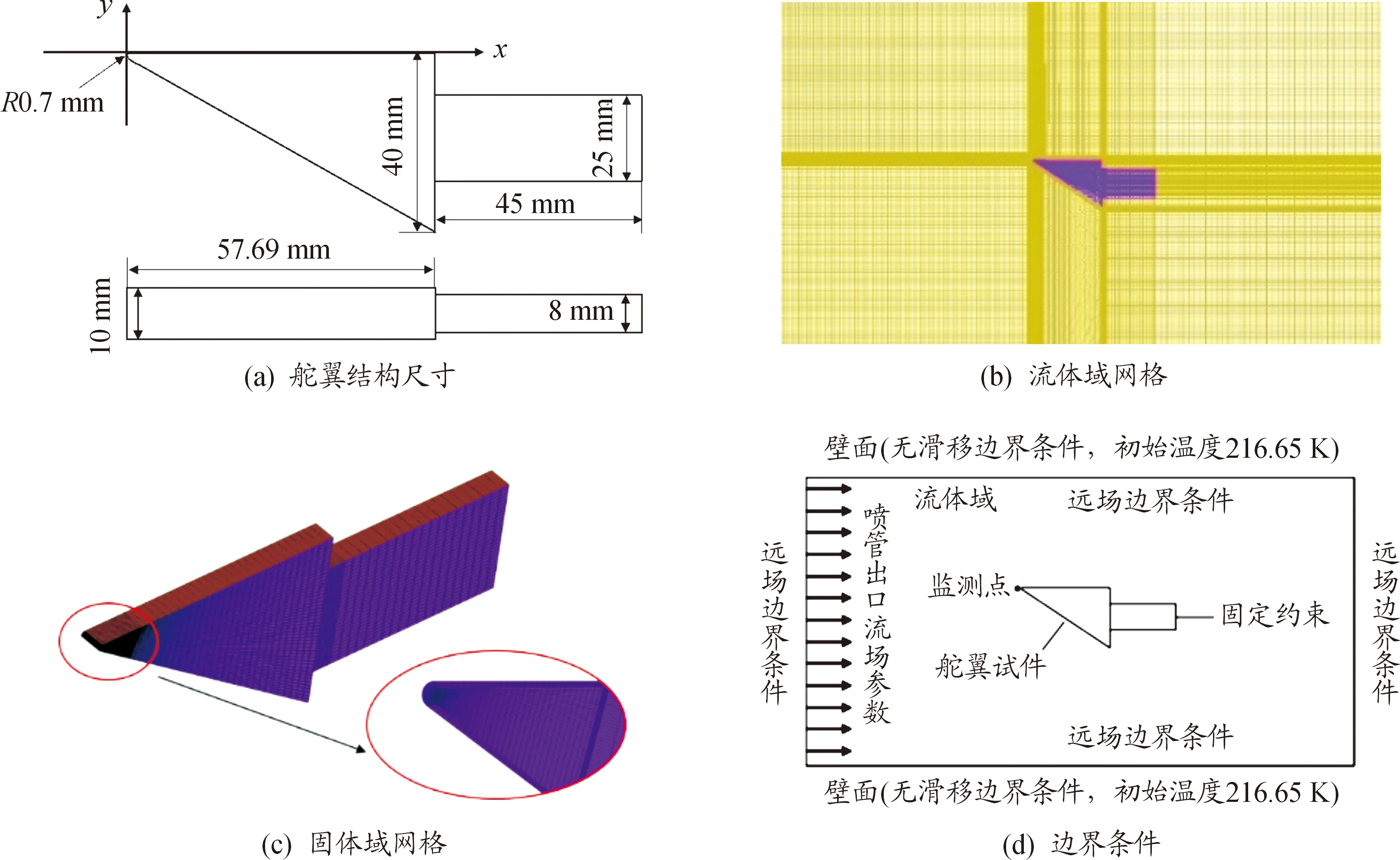
圖7 舵翼結構與計算域網格

表4 D6AC鋼材料參數

為了分析舵翼結構在近空間飛行狀態下的氣動力、氣動熱與結構響應之間的關系，將仿真工況設置為耦合計算(考慮氣動力、氣動力耦合效應)、僅氣動熱計算(僅考慮熱變形)、僅氣動力計算(僅考慮氣動力變形)和無結構變形因素計算4種工況。

3.2 結構變形分析

舵翼結構在X、Y、Z3個方向發生變形，在不同迎角狀態下發生拉壓、彎曲和熱膨脹變形，結構在Z方向只發生熱膨脹變形而無拉壓和彎曲變形，因此只對舵翼結構X方向(縱向)和Y方向(橫向)的變形進行分析。

對舵翼結構施加耦合工況，圖8為不同迎角狀態下的舵翼結構縱向變形云圖，圖9為舵翼結構不同位置的縱向變形曲線，其中橫坐標為舵翼結構所處位置，X=0處為前緣頂端位置，如圖7(a)所示。

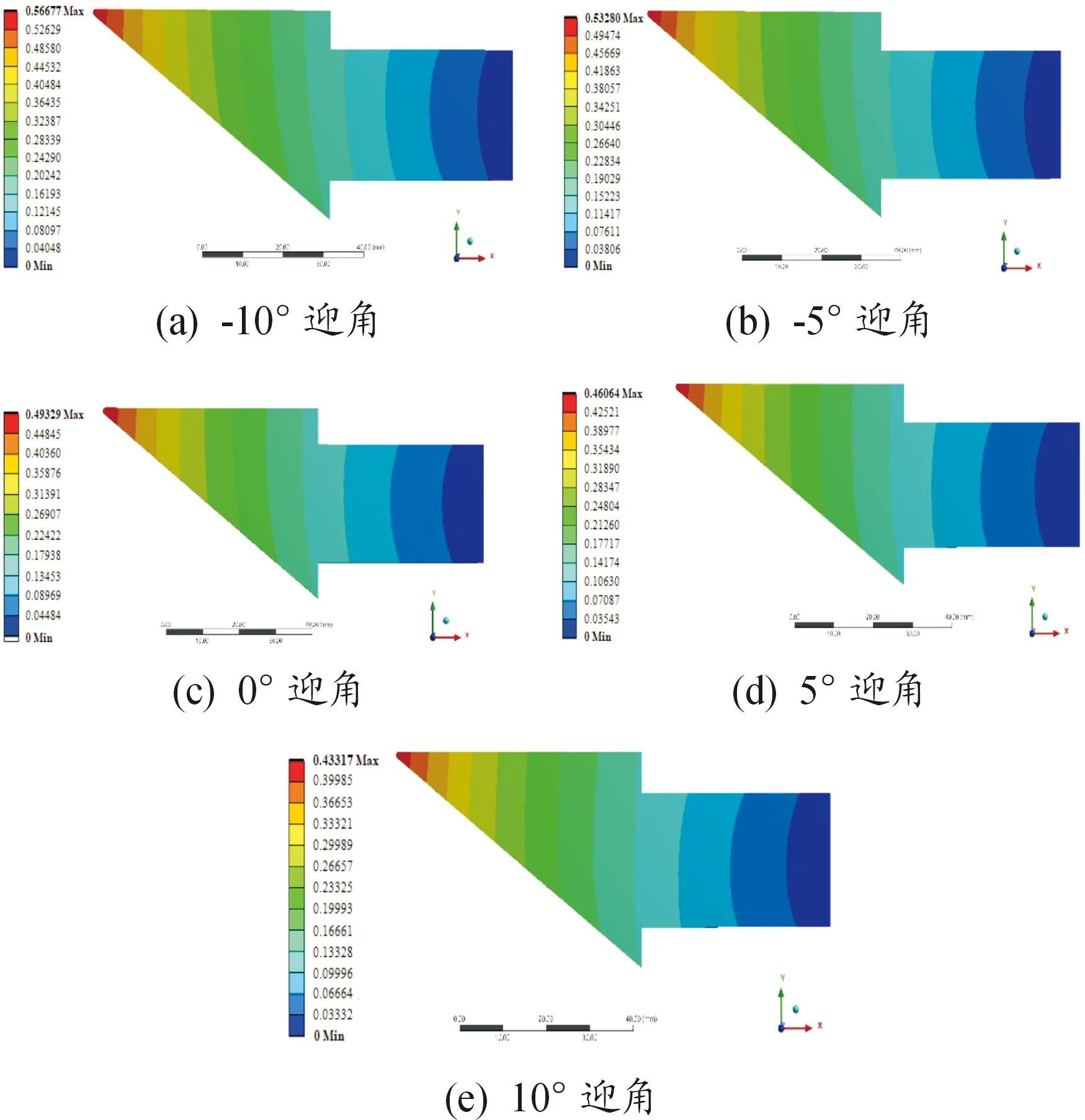
圖8 舵翼結構X方向變形云圖

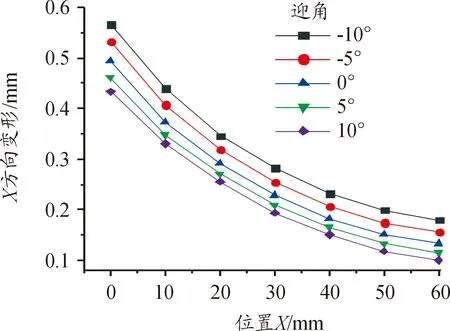
圖9 舵翼結構不同迎角下縱向變形曲線

舵翼結構在近空間飛行狀態下發生氣動加熱現象，使舵翼結構產生縱向變形。由于舵翼結構尾部采用固定約束，類似于懸臂梁受載方式，當迎角為-10°時，舵翼結構尖角的平分線與來流方向夾角最小，此時舵翼結構彎曲撓度最小，而縱向變形量最大。隨著迎角增大撓度隨之增加，縱向變形量逐漸減小。

圖10為舵翼結構不同位置的橫向變形曲線，與縱向變形規律不同，隨著迎角增大，橫向變形量逐漸增大。舵翼結構尾部采用固定約束，受到橫向氣動力作用，發生彎曲變形。另一方面，由于氣動加熱使結構發生熱膨脹，迎風側溫度較高，膨脹量大，背風側溫度低，膨脹量小，造成舵翼結構沿背風側發生彎曲。在氣動力和氣動熱的共同作用下，舵翼結構發生彎曲變形，迎角越大，上述現象越明顯，橫向變形量也就越大。

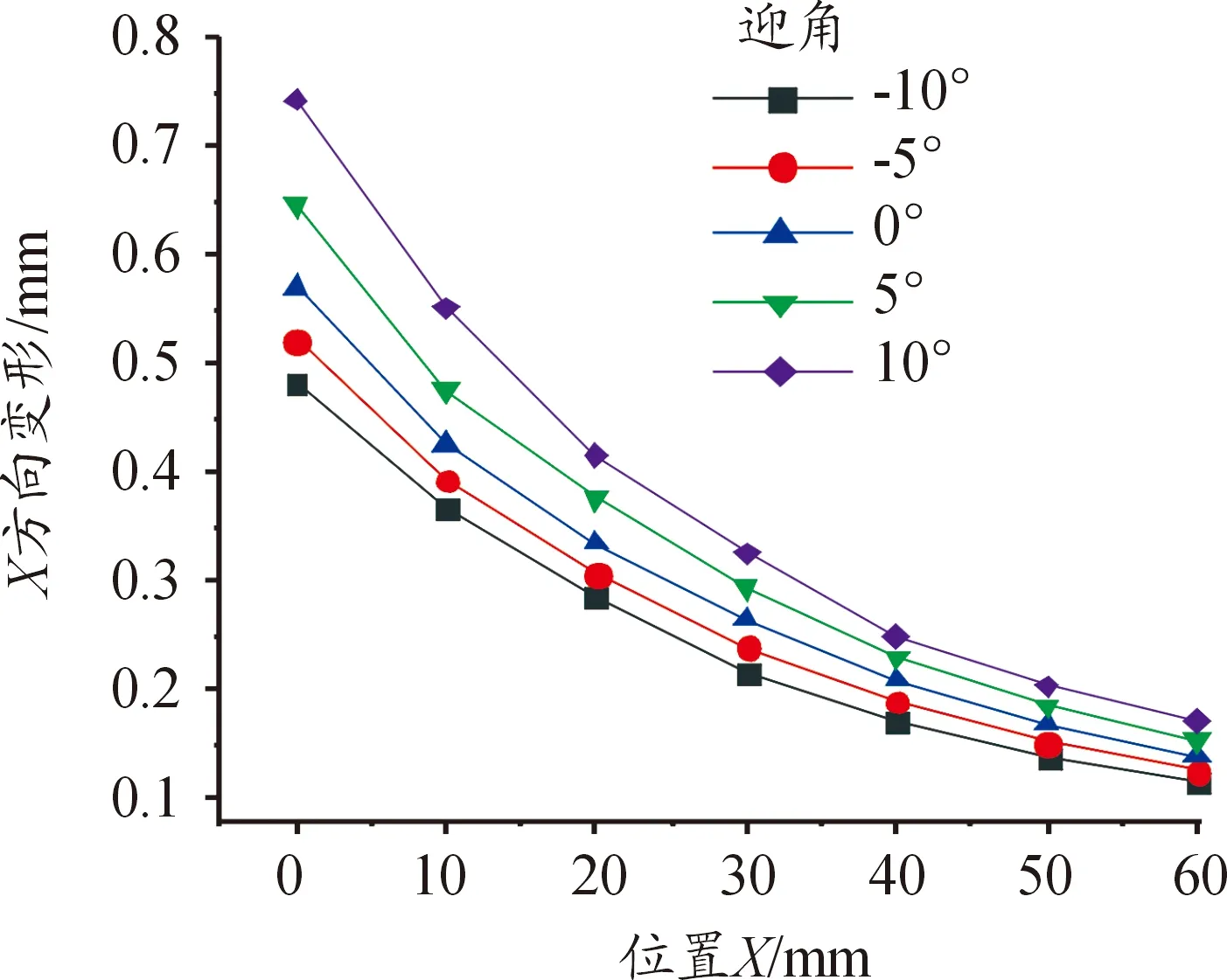
圖10 舵翼結構不同迎角下橫向變形曲線

對比圖9、圖10數據可知，當舵翼結構迎角較小時，以縱向變形為主，橫向變形較小，隨著迎角增大，橫向變形明顯增大并超過縱向變形。為了進一步分析上述變形規律產生的原因，對氣動熱、氣動力以及耦合作用下的橫向、縱向變形進行分析。

舵翼結構縱向變形如圖11所示，單純氣動熱作用下的變形量略大于耦合作用，二者變化規律一致，相差很小；而氣動力對舵翼結構造成壓縮變形，變形量隨迎角增大而降低，由于變形量非常小，對整體縱向變形的影響可以忽略。因此，舵翼結構縱向變形主要由氣動熱的作用引起，氣動力作用極小，氣動熱與氣動力的耦合作用不明顯。

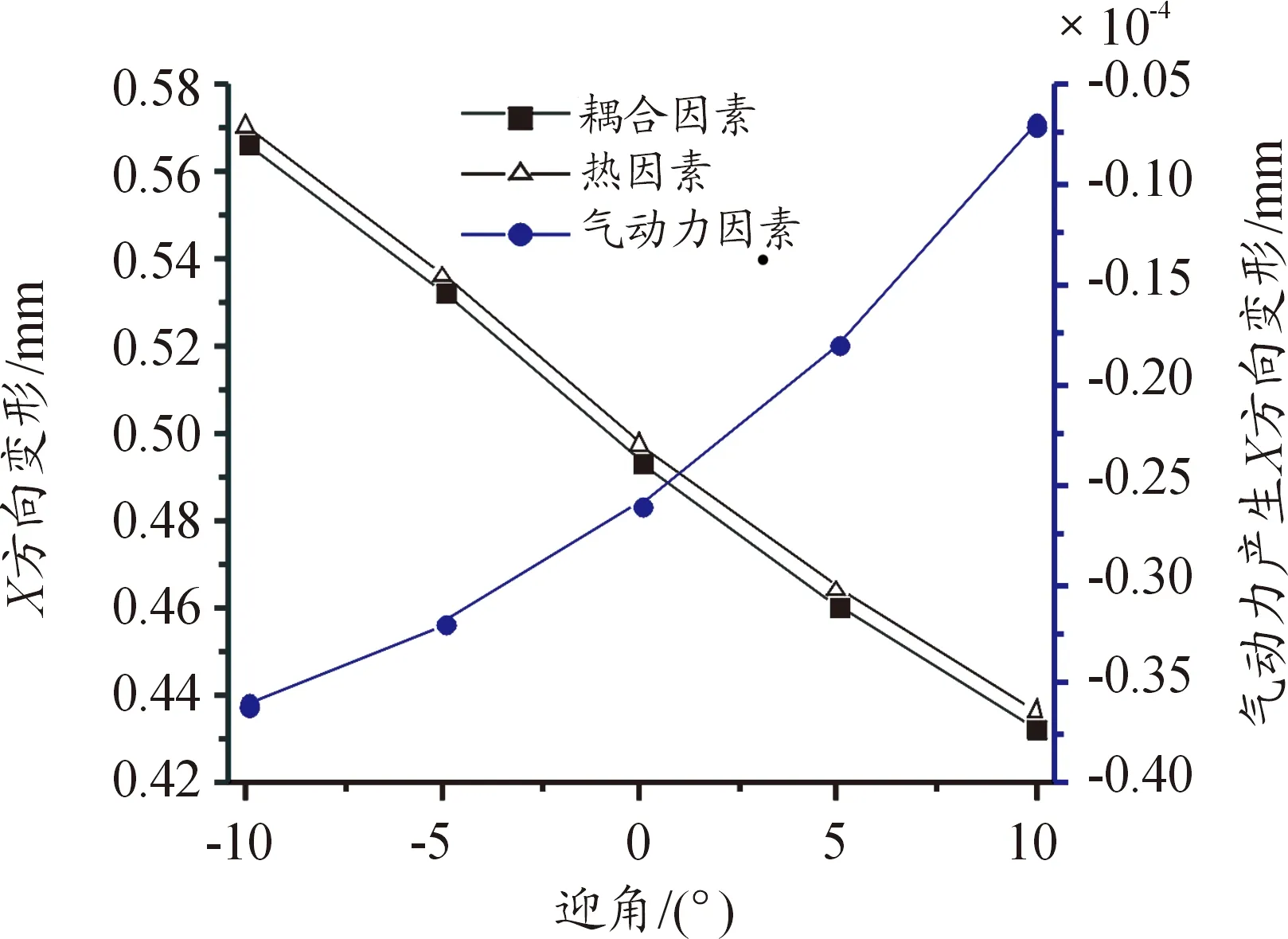
圖11 縱向變形曲線

舵翼結構橫向變形如圖12所示，在氣動熱因素作用下變形為0.400 42～0.459 53 mm；在氣動力作用下橫向變形量較縱向變形量明顯增大，但仍然很小，僅為0.000 01～0.000 08 mm。當氣動熱與氣動力耦合作用時，變形量明顯增大，達到為0.484 30～0.633 66 mm，可見耦合效應在變形量上體現得比較明顯。在單純氣動力作用下，舵翼構件并沒有發生明顯的彎曲變形。在氣動熱耦合作用下，舵翼結構溫度急劇升高，材料物性參數發生明顯變化，彈性模量大幅降低，導致發生了更大的變形。彎曲變形改變了結構的氣動外形，使溫度場進一步升高，一方面加劇了因舵翼結構熱膨脹和熱彎曲導致的變形，另一方面繼續降低了材料的彈性模量，使結構產生了更大的變形。在二者的耦合作用，橫向變形量較單獨氣動熱和單獨氣動力作用下有著明顯的升高，迎角越大，氣動力與氣動熱作用的耦合效果越明顯。

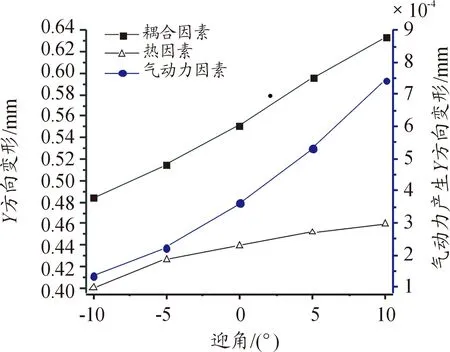
圖12 橫向變形曲線

3.3 溫度分析

對舵翼結構施加耦合工況，圖13為不同迎角狀態下的溫度分布云圖，舵翼結構前緣處氣動熱效果最明顯，溫度最高，沿尾部方向逐漸降低。由于舵翼結構前緣尖角相對氣流方向不是對稱的，上下面迎風角度不同，導致溫度分布也不相同。下表面與來流形成的角度更大，氣動熱更劇烈，溫度更高。隨著迎角增大，下表面氣動熱效果進一步加劇，溫度進一步升高。

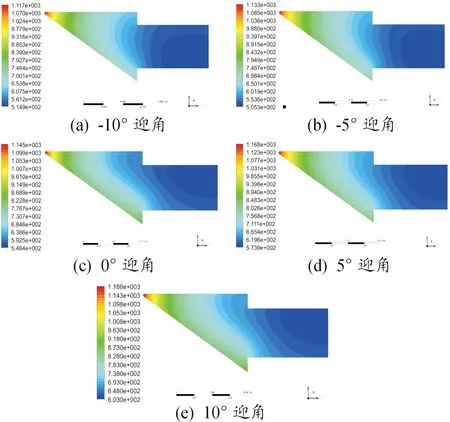
圖13 舵翼結構溫度云圖

對舵翼結構溫度場受氣動熱力耦合效應的影響規律進行研究，不同耦合因素下最高溫度隨迎角變化曲線如圖14所示。在3種耦合狀態下，溫度都隨迎角增大而升高。在只考慮氣動熱因素時，整體溫度最低；在無結構變形耦合因素中，只考慮了舵翼結構的熱膨脹而不考慮氣動力導致的變形，這時溫度較只考慮氣動熱時略高，可見單純熱膨脹變形能夠小幅度增加氣動熱效應；在完全耦合因素中，溫度明顯大于上述2個工況，且迎角越大差值越高。由于在大迎角姿態飛行時，舵翼結構受氣動熱和氣動力作用發生變形，使迎角進一步增大，導致氣動加熱作用更加劇烈，進而升高了舵翼結構的溫度。可見，迎角越大，氣動熱與氣動力耦合效應對結構溫度場的影響就越明顯。

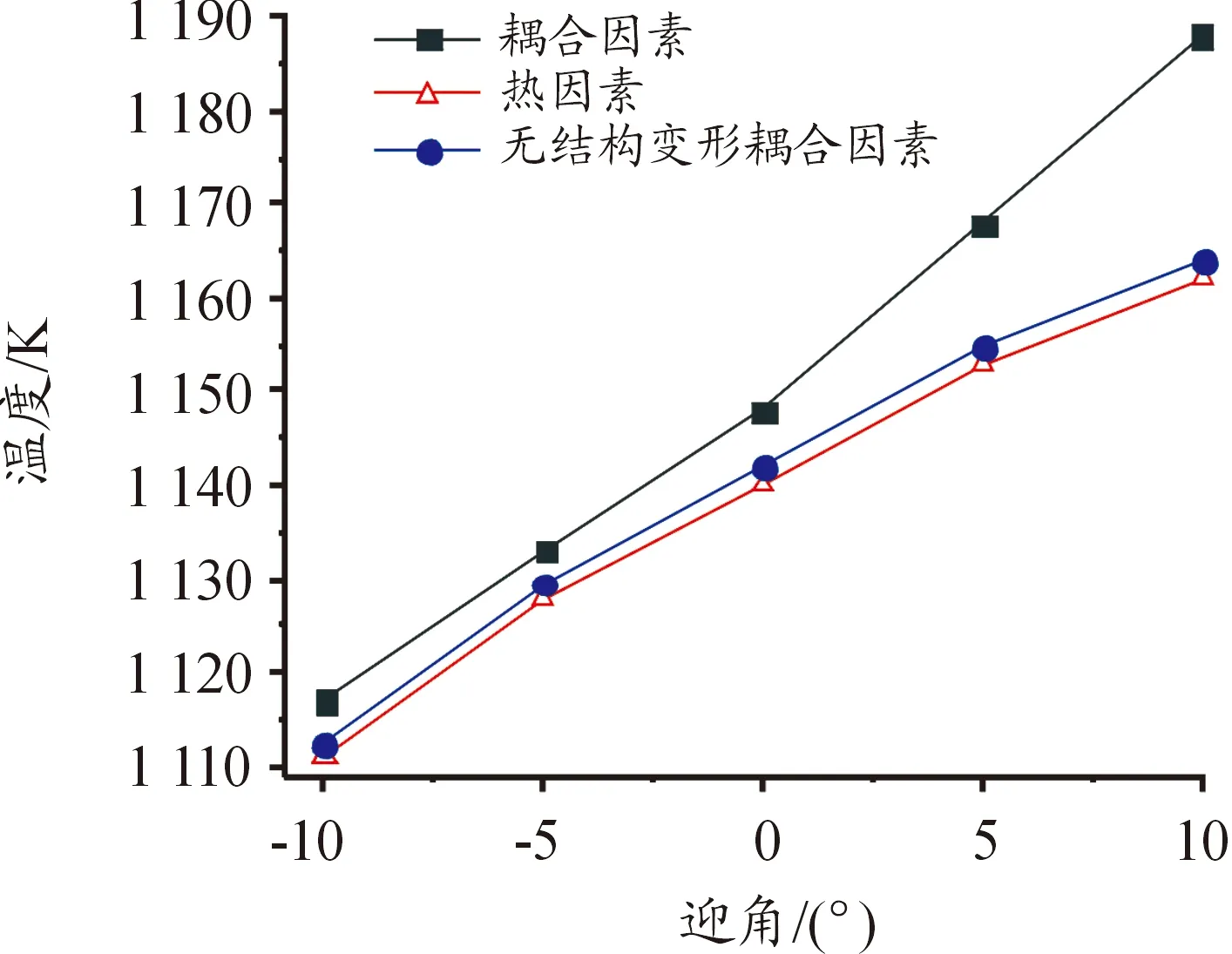
圖14 舵翼結構溫度曲線

4 結論

1) 在近空間飛行狀態下，舵翼結構頭部尖角處的溫度、變形最大，隨著飛行迎角增大，溫度升高，縱向變形減小，橫向變形增大。

2) 在近空間飛行狀態下，舵翼結構會發生縱向拉伸和橫向彎曲變形，縱向拉伸變形主要由氣動加熱引起，橫向變形主要由氣動力作用引起。

3) 在近空間飛行狀態下，舵翼結構氣動熱、氣動力的耦合效應使變形與溫度增大；飛行迎角越大，耦合效應越明顯。因此，當舵翼結構以大迎角狀態飛行時，氣動熱力環境會更加惡劣，在熱防護設計和結構設計時應充分考慮耦合效應。