舵機系統工作模態特性仿真

李杰光，梁 建，王春艷，段麗華，朱劍波

(1 中國空空導彈研究院， 河南 洛陽 471009； 2 河南科技大學 軟件學院， 河南 洛陽 471003)

高速飛行的導彈依靠作用于舵面的氣體來流形成鉸鏈力矩穩定和控制彈體，使導彈按需要的彈道飛行。舵系統作為導彈飛控系統的執行機構，其性能的好壞直接決定了導彈飛行過程的動態品質。導彈高速飛行過程中舵面氣動力、彈性力與慣性力存在耦合作用，舵面氣動載荷改變舵系統剛度和動態特性，當相對氣流速度超過臨界速度時，瞬時氣動載荷可使舵面振動失穩，從而發生顫振[1-3]。

由于電動舵機技術具有成本低、動態特性好、易于控制等優點，使得其在導彈舵系統中得到廣泛應用。隨著導彈對舵系統傳動精度、響應速度和穩定性要求的不斷提高，舵系統的動態特性、輸出響應和振動穩定性的影響變得越加突出。舵機傳動機構零部件存在的間隙與彈性變化增大了傳動機構的非線性因素，使得舵系統響應曲線出現滯后和削波[4，5]。隨著導彈攻角和飛行馬赫數的增加，舵面與氣動力的耦合作用，使得舵面振動位移趨向于臨界振動狀態[6]。舵機傳動機構各環節的接觸剛度、阻尼、間隙等因素會影響舵系統的動態特性，且傳動鏈末級參數對系統動態特性的影響更為明顯[7，8]。對舵機傳動機構進行優化設計，合理控制間隙、摩擦、彈性變形等非線性因素，可有效降低舵機控制模塊和導彈控制系統的復雜度，降低系統成本[9]。

近年來，多學科仿真與虛擬樣機技術在航空航天領域設計研發中的優勢日益突顯。空空導彈作為現代主流空戰精確制導武器，在舵系統氣動力載荷、傳動機構動態響應、結構的彈性變形方面的系統性研究較少[10]。因此，本文針對某型空空導彈單通道舵系統傳動機構進行動態特性、結構彈性變形、舵面氣動力研究，研究結果對系統設計和工程應用具有指導意義。

1 舵面顫振/動力學仿真建模

1.1 理論方程

在線性不發生改變的條件下，對于一連續的、非線性物理結構描述的自由振動方程為：

M·x(t)+C·x(t)+K·x(t)=f(t)

式中：M表示系統質量矩陣列；C表示系統阻尼矩陣；K表示系統剛度矩陳；x(t)表示系統位移響應向量；f(t)表示系統激勵力的向量。

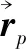
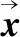
1.2 動力學仿真建模與驗證

彈載計算機發出的飛控信號經由控制器和功率放大器控制電機轉動，電機轉矩經由兩級齒輪傳動和滾珠絲杠副減速，絲杠螺母帶動搖臂擺動，搖臂帶動舵軸轉動，最終由舵軸控制舵面的偏轉位置角度。依據舵機傳動機構工作原理建立動力學仿真模型，動力學仿真模型簡圖如圖1所示，動力學仿真模型環節設置如圖2所示。

圖1 舵機傳動機構動力學模型簡圖

圖2 動力學模型環節設置示意圖

兩級齒輪傳動的彈性變形可等效簡化為輸出級齒輪內外圈間的扭轉彈簧，扭轉彈簧剛度K1=1×104N·m/(°)，阻尼c1=2.1×10-6N·m·s/°。絲杠兩端軸承可等效為兩個阻尼器，剛度K3=1.0×108N/m，阻尼c3=10 N·s/m。絲杠螺母與撥叉間定義為三向力，間隙可采用BISTOP函數進行模擬，剛度K2=4.2×108N/m，阻尼c2=2.1×102N·s/m，間隙e=5×10-4m[11]。舵軸兩端由兩軸承支承，動力學建模時將靠近舵面一端的軸承等效為球鉸副，遠離舵面一端的軸承等效為阻尼器，通過設定阻尼器剛度值可模擬軸承剛度的變化。阻尼器剛度K4=1.0×108N/m，阻尼c4=100 N·s/m。將傳動機構的摩擦阻力可等效為舵軸與本體間的摩擦力矩，模型中可將摩擦力矩施加于舵機與本體間的球鉸副，舵軸與本體間初始摩擦力矩設置為Ff=6 N·m。

舵機傳動機構動力學模型輸入、輸出通道數據采集點位置如圖3所示。其中點I處為輸入通道，點O1～O8處為輸出通道，舵面坐標系定義如圖3中所示。

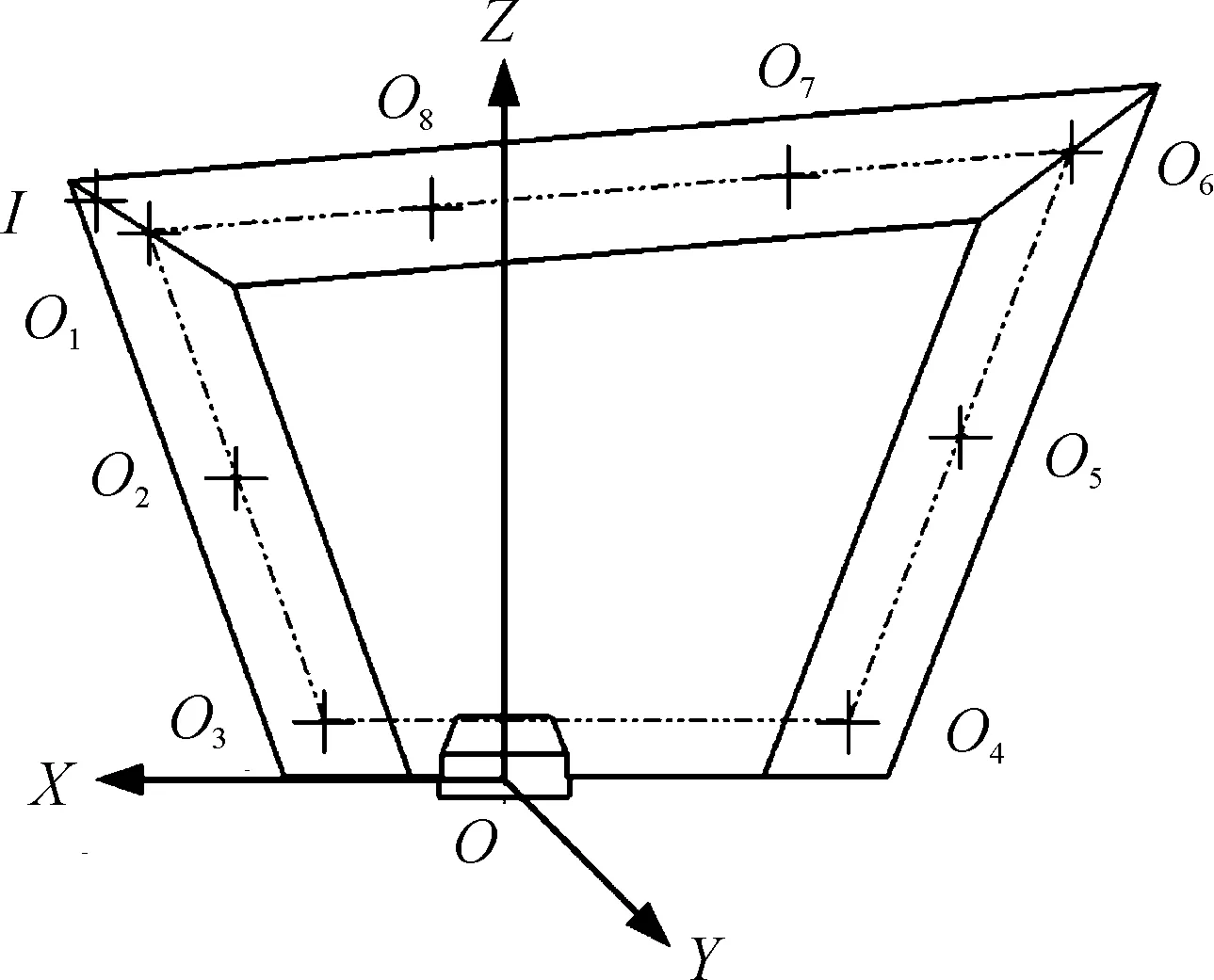
圖3 舵面振動輸入、輸出通道數據采集點位置示意圖

由參考文獻[7]可知，舵系統傳動機構一階振型為舵面彎曲振動，二階振型為舵面扭轉振動。工程中主要關注前兩階模態頻率，本文中選取前兩階模態仿真結果與實驗結果進行了對比，以達以模型驗證的目的。仿真計算得出的舵機傳動機構各階模態與振型描述如表1所示。

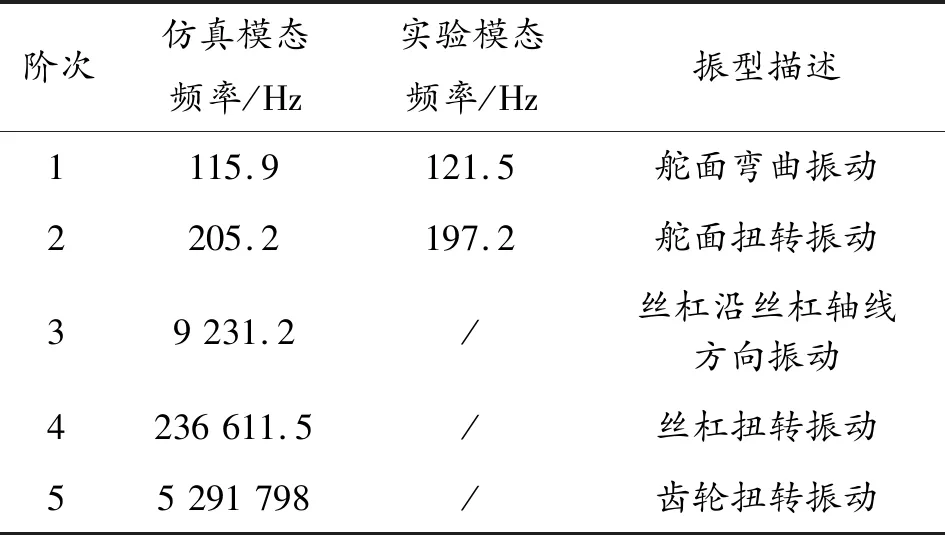
表1 各階模態頻率及振型描述

傳動機構模態數值與實驗結果對比，一階模態差為5%以內，二階模態差為5%以內，從而驗證動力學仿真模型建模的正確性。

1.3 氣動力仿真建模

導彈飛行3馬赫數飛行，攻角為30°時，舵機與氣動力雙向流固耦合模型。舵面與氣動力流固耦合仿真模型如圖4所示，具體模型參數設置參見參考文獻[6]。

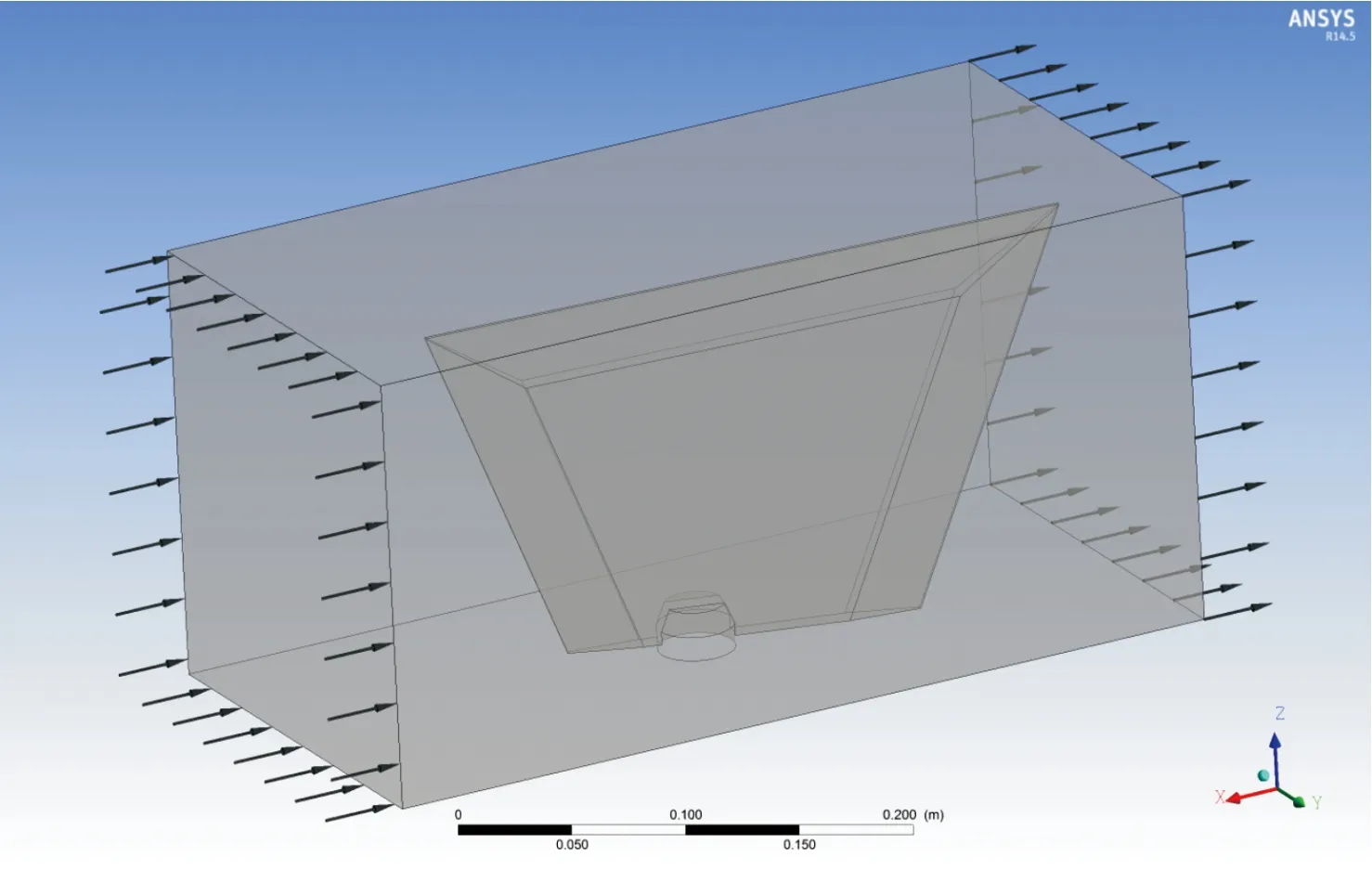
圖4 舵面與氣動力流固耦合仿真模型示意圖

雙向流固耦合氣動力作用點坐標：(14.8，-6.4，59.7)，單位：mm。對比X、Y、Z三方向作用力值，Y方向作用氣動力對舵面振動最為顯著，因此，選取Y向氣動載荷作用舵面外部激勵。導彈飛行速度為3馬赫，攻角為30°時，氣動力Y向分量變化曲線如圖5所示。

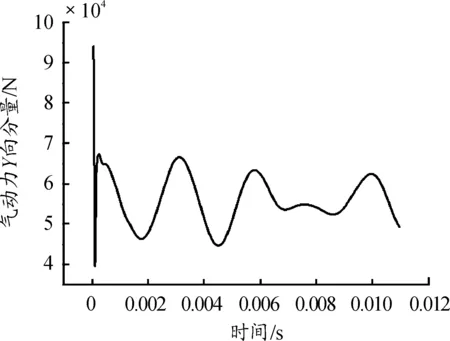
圖5 舵面Y向氣動力變化曲線

1.4 剛柔耦合仿真建模

為獲得剛柔耦合對舵系統模態頻率的影響關系，需對舵系統重要零部件進行柔性化處理，選取舵系統傳動機構中撥叉為柔性化處理對象。

采用ANSYS軟件對撥叉進行模態中性文件(mnf文件)生成，采用Adams軟件將零件的mnf文件導入動力學模型中對撥叉進行柔性化處理。生成mnf文件過程中，不同材料參數可通過設置有限元單元屬性進行調整。搖臂與外部剛體的連接點分別選擇位于搖臂回轉軸和絲杠螺母中心處，搖臂的網格模型及外部連接點如圖6所示。

圖6 搖臂剛柔耦合模型示意圖

運用Adams的Flexible Bodies單元導入mnf文件將剛體模型進行柔性化處理。將柔性體搖臂的Marker點與剛性體關聯。采用Adams的Vibration模塊進行模態仿真分析，可直接讀取仿真模態頻率結果。

2 結果與討論

2.1 摩擦力矩、剛度對系統模態特性的影響

由圖1動力學模型簡圖可知，舵軸一端的剛度對傳動機構一階彎曲模態影響較大，舵軸與本體間的摩擦力矩對傳動機構的二階扭轉模態的影響較大。

2.1.1摩擦力矩對舵機傳動機構模態特性的影響

通過設置摩擦力矩參數和調整摩擦力預載荷值調整舵機與本體摩擦力矩值。運動輸入電機齒輪角位移設定0.05 rad/s角頻率的正弦信號，舵軸與本體摩擦力矩變化曲線圖如圖7所示，由圖7可知，一個工作周期內摩擦力矩隨舵軸偏轉位置而變化。

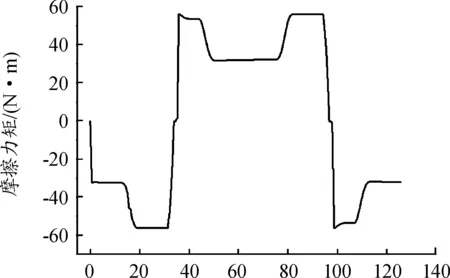
圖7 摩擦力矩變化曲線

軸承剛度K41=1×107N/m、K42=1×108N/m時，改變摩擦力矩舵機傳動機構前兩階模態影響變化曲線如圖8所示。由圖8曲線變化趨勢可知，增大摩擦力矩可提高舵機傳動機構的彎曲和扭轉剛度，進而提高了一、二階模態頻率。隨著摩擦力矩的增大，二階模態頻率近似線性增大。當摩擦力矩Tf>38 N·m時，一階模態曲線逐漸趨180 Hz臨界值，摩擦力矩的變化對一階模態的影響在減小；摩擦力矩Tf<38 N·m 時，摩擦力矩的變化對一階模態的影響較大。

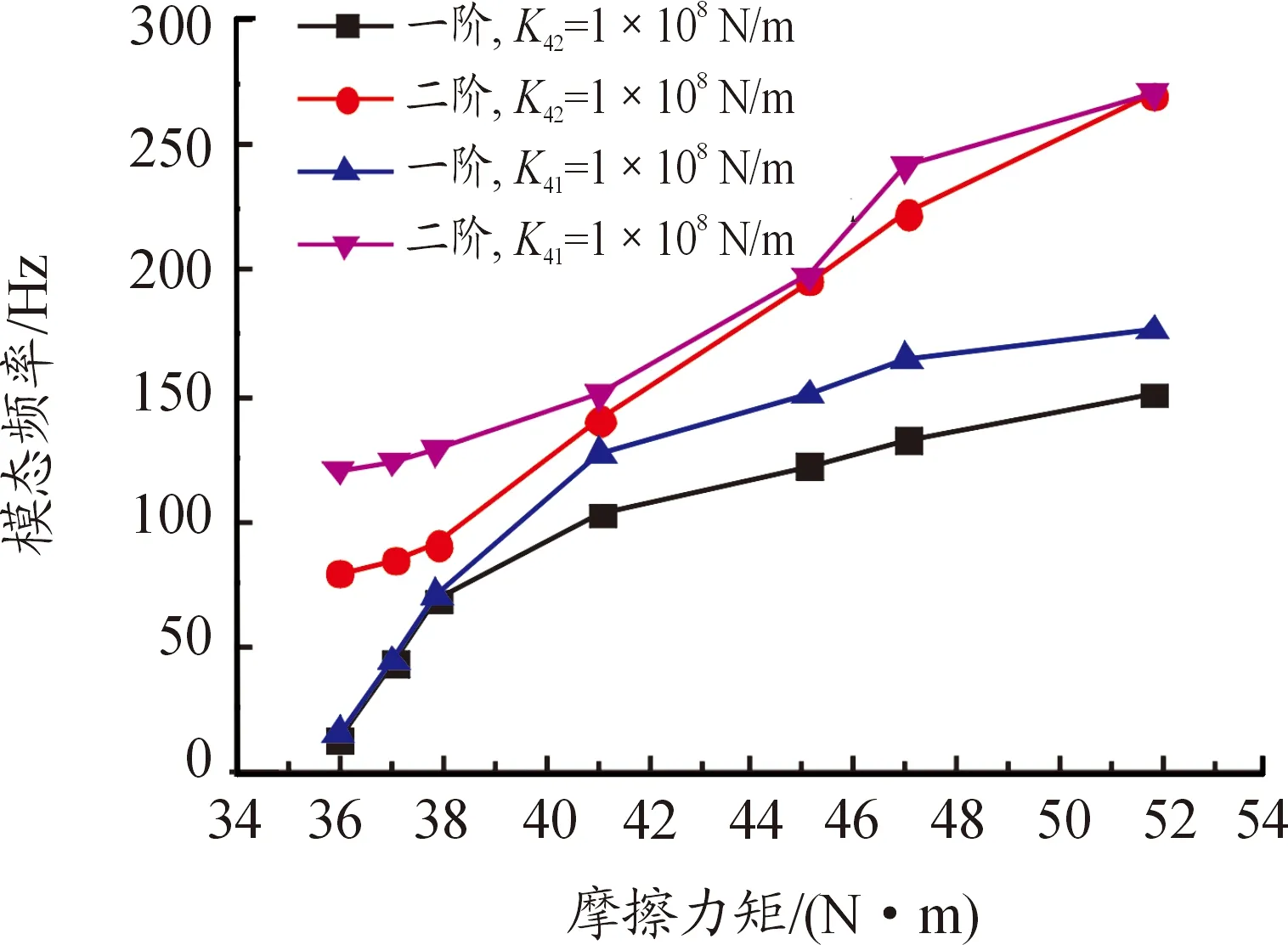
圖8 模態與摩擦力矩變化曲線

由于球鉸副具有兩個轉動自由度，摩擦力矩對舵面彎曲振動和扭轉振動均有影響。軸承剛度一定的條件下，摩擦力矩Tf<38 N·m時，摩擦力矩對舵面彎曲剛度的影響起主導作用，一階模態頻率隨摩擦力矩的增加其增大趨勢更為明顯；摩擦力矩Tf>38 N·m時，軸承剛度對舵面彎曲剛度的影響起主導作用，因此，增大摩擦力矩舵系統一階模態頻率曲線變化平緩。摩擦力矩對于舵面扭轉剛度的影響起主導作用，因此，增大摩擦力矩，二階模態逐漸增大。

2.1.2剛度對舵機傳動機構模態特性的影響

摩擦力矩為Tf1=37.85 N·m、Tf2=45.10 N·m時，改變舵軸一端軸承剛度K4，軸承剛度變化對舵機傳動機構一、二階模態影響變化曲線如圖9所示。Tf1=37.85 N·m時，軸承剛度K4>4×106N/m時，增大軸承剛度，一階模態頻率基本不變。Tf2=45.10 N·m時，軸承剛度K4>2×107N/m時，增大軸承剛度，一階模態頻率基本不變。因此，舵機傳動機構一階模態受到軸承剛度和摩擦力矩的雙重影響，提高舵機傳動機構的舵面彎曲剛度增大一階模態頻率，既要提高軸承剛度，又要提高扭轉摩擦力矩。

圖9 模態與軸承剛度變化曲線

不同摩擦力矩，增大軸承剛度均可提高舵機傳動機構的扭轉剛度，提高二階模態頻率。同時，小摩擦力矩條件下，軸承剛度較小時，改變剛度值對二階模態的影響較小。增大摩擦力矩，可同時通過增大軸承剛度提高舵系統一階彎曲剛度。

2.2 結構彈性變形對系統模態特性的影響

對搖臂進行柔性化處理，選擇兩種材料(不銹鋼、鋁合金)，對比搖臂的柔性變形、材料對舵機傳動機構模態的影響。柔性變形及不同材料條件下傳動機構前三階模態如表2所示。

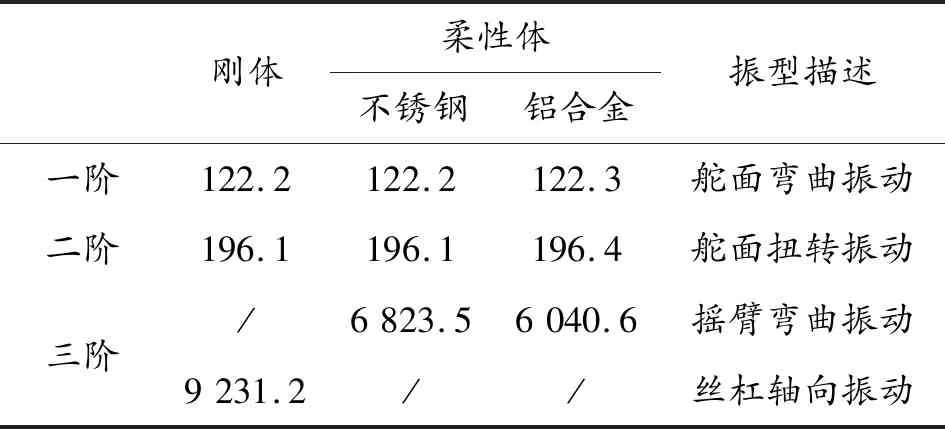
表2 考慮柔性變形及材料的傳動機構前三階模態

由表2可知，考慮搖臂的彈性變形對舵機傳動機構前兩階模態數值及振型的影響較小，對三階模態與振動的影響較大。由3.1節分析可知，舵機傳動機構的一、二階模態主要受摩擦力矩和軸承剛度的影響，因此，考慮搖臂彈性變形及更換材料對舵機傳動構一、二階模態的影響較小。零部件的彈性變形會降低傳動機構的剛度，因此，零部件剛度越小，傳動機構三階模態頻率越小。并且零部件的彈性變形亦會改變傳動機構振型，剛體模型的三階振型為絲杠軸向振動，柔性體模型的三階振型為搖臂彎曲振動。因此，提高舵機傳動機構末級零部件的剛度對提高傳動機構模態頻率作用更有效。

3 結論

1) 軸承剛度一定時，提高作用于球鉸副間的摩擦力矩可提高舵系統一、二階模態頻率，增強舵系統舵面的彎曲和扭轉剛度。摩擦力矩Tf<38 N·m時，摩擦力矩對舵面彎曲剛度的影響起主導作用；摩擦力矩Tf>38 N·m時，軸承剛度對舵面彎曲剛度的影響起主導作用，增大摩擦力對增大一階模態頻率增加的幅度減小。

2) 摩擦力矩一定時，增在軸承剛度可使舵系統二階模態頻率逐漸增大。大摩擦力矩條件下，軸承剛度較小時，改變剛度值對二階模態的影響較小。隨著軸承剛度的增大，Tf1=37.85 N·m，K4超過4×106N/m時，一階模態頻率基本不變；Tf2=45.10 N·m，軸承剛度K4超過2×107N/m時，一階模態頻率基本不變。增大摩擦力矩，可同時通過增大軸承剛度提高舵系統一階彎曲剛度。

3) 改變搖臂由剛體模型為柔性剛體對舵系統的一、二階模態的影響較小。搖臂的彈性變形可降低舵系統的三階模態，變形量越大，三階模態頻率越小；同時，舵系統三階振型亦發生相應的改變。