非耦合韌性斷裂準則及其在航空金屬材料中的應用

馬宏越, 肖納敏, 錢 鵬, 羅 帥, 章海明*

（1．上海交通大學 塑性成形技術與裝備研究院，上海 200030；2．中國航發北京航空材料研究院 航空及發動機材料應用評價中心，北京 100095；3．上海科學技術交流中心，上海 200003）

先進材料的研發和應用是航空航天技術發展的支撐和保障，其中金屬材料如鋁合金、鈦合金、鎂合金、超高強度鋼和高溫合金等是航空領域主要的結構材料[1-2]。隨著航空航天工業的快速發展，輕質、高強、高韌金屬材料的需求和應用日益增加，其加工成形性能、服役性能和安全可靠性的預測與評估至關重要。材料的損傷斷裂預測一直是加工制造工藝設計的關鍵，國內外學者開展了大量關于金屬材料損傷斷裂的微觀機理和斷裂準則的研究，這對材料的選擇、成形工藝的設計和優化等都具有重要的指導意義。

盡管金屬材料斷裂行為的研究已有近百年歷史，但預測材料在復雜變形路徑下的損傷斷裂行為仍極具挑戰。根據塑性變形和損傷斷裂之間的相互作用關系，韌性斷裂準則一般可分為耦合型和非耦合型兩大類。耦合型損傷模型考慮損傷演化對材料力學性能和變形能力的退化作用；而非耦合斷裂準則不考慮損傷對塑性變形的影響，通常以宏觀物理量作為斷裂發生的判據[3]。耦合型模型通常又可以分為以Gurson-Tvergaard-Needleman（GTN）模型[4-5]為代表的細觀力學損傷模型和以Lemaitre模型為代表的連續損傷力學（continuous damage mechanics，CDM）模型[6-7]。經典的GTN模型適用于中高應力三軸度、拉伸型斷裂為主的變形模式，而無法描述剪切型斷裂行為。Nahshon等[8]和Xue[9]在GTN模型中引入剪應力對損傷演化的影響，以預測低應力三軸度下的斷裂行為和應變集中軟化效應。Lemaitre[6-7]在CDM理論框架下，引入了宏觀損傷因子及其演化模型以描述損傷演化及其對材料性能惡化的影響。Cao等[10]對CDM模型進行拓展，考慮了Lode角參數的影響，使其更好地預測材料的剪切變形。

耦合型損傷斷裂模型考慮了塑性變形和損傷演化的相互作用，塑性變形影響損傷狀態變量的演化，損傷的發展則導致材料剛度和強度衰減，因此更符合材料變形和損傷發展的實際物理過程，但耦合“塑性-損傷”本構模型的建立、數值實現以及參數標定通常較復雜。相比之下，非耦合型斷裂準則盡管忽略了損傷演化對材料力學性能的動態影響，但其模型參數少、實驗標定容易，因此在工程中得到廣泛應用，盛行于主流商業軟件，如LS-DYNA和ABAQUS等。Dunand等[11]通過TRIP780板料比較了Gurson模型[4]和非耦合Mohr-Coulomb斷裂準則[12]的預測能力，其結果表明這兩種模型均能很好地預測不同應力狀態下的裂縫位移；并建議將Mohr-Coulomb斷裂模型用于工程應用，以提高計算穩定性并簡化模型參數的識別。

本文首先介紹金屬材料韌性斷裂微觀機理，然后回顧非耦合韌性斷裂預測模型的研究進展，并重點評述幾種典型的韌性斷裂模型及其應用，最后展望非耦合韌性斷裂模型的發展趨勢。

1 金屬材料的損傷斷裂機理

1.1 韌性斷裂的微觀機制

金屬材料在發生較大塑性變形后一般會發生韌性斷裂，在載荷和微觀組織的聯合作用下，材料內部形成剪切帶、微空洞、微裂紋等微細觀缺陷（損傷），損傷累積導致材料最終的失效斷裂。金屬材料韌性斷裂的主要機制有：（1）剪切和壓縮應力主導下的剪切型斷裂[9，13-16]，如圖1（a）所示（①變形過程中空洞形核，②空洞沿剪應力方向長大，③沿剪應力方向空洞連接，材料發生斷裂）；（2）拉應力主導下的空洞的形核、長大與聚合[9，13-16]，如圖1（b）所示（①空洞形核，②空洞沿拉應力方向長大，③空洞相互連接導致材料斷裂）；（3）空洞-剪切復合型機制[14，17]。在外力作用下，夾雜物、第二相粒子與基體的界面處以及晶界、相界、孿晶界和位錯塞積處容易出現高的應力集中，導致空洞形核和微裂紋萌生。剪切帶上的空洞會降低滑移帶的承載能力，導致應變集中，進一步導致空洞沿著剪切帶長大拉長直至材料的分離。因此，金屬材料的損傷斷裂行為受材料的強度、微觀組織和應力狀態的共同影響。

圖1 空洞的形核、長大與聚合示意圖 （a）剪切型損傷；（b）拉伸型損傷Fig. 1 Schematic diagram of voids nucleation，growth and coalescence （a）shear fracture dominated mechanism；（b）tensile fracture dominated mechanism

宏觀上，金屬材料的損傷斷裂行為受變形路徑、應力狀態和塑性各向異性的影響；微觀上，金屬多晶體材料的損傷斷裂受其微觀組織（如晶粒大小、形狀、取向、織構、第二相的尺寸與分布等）和材料強度（如加工硬化）等的影響。當前的損傷斷裂模型尚未實現對微觀組織影響的量化，主要考慮宏觀影響因素，特別是關于應力狀態的作用規律，一直是韌性斷裂準則研究的重點。

1.2 應力狀態的影響

應力狀態是影響材料損傷斷裂行為的關鍵因素，各向同性材料的力學性能和坐標系無關，因此通常采用三個主應力 σ1、 σ2和 σ3表述材料的應力狀態，如圖2（a）所示。相應地也可以采用應力張量的三個不變量或它們之間的無量綱參數，如應力三軸度 η和Lode角參數[18]等來描述：

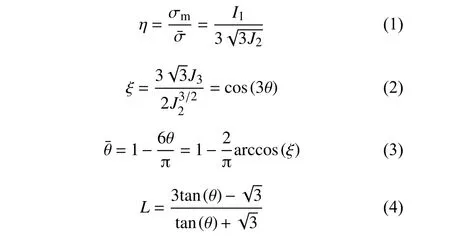
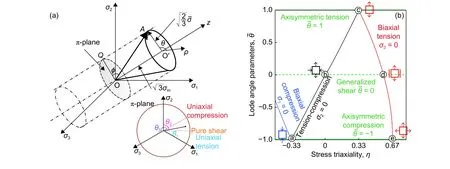
圖2 各向同性材料 （a）主應力空間中的羅德角；（b）平面應力條件下的羅德角參數與應力三軸度之間的關系Fig. 2 Isotropic materials （a）Lode angle in the principal stress space；（b）relationship between Lode angle parameter and stress triaxiality for plane stress conditions

式中：I1為 應力張量的第一不變量；J2和J3為偏應力張量的第二和第三不變量；σm=(σ1+σ2+σ3)/3為平均應力，為等效應力；ξ為偏應力張量的正則第三不變量；θ為Lode角；為Lode角參數；L為Lode參數；θ、和L具有等效的物理意義，描述應力狀態偏離純剪切應力狀態的程度，且?1表示純剪切應力狀態（η=0）或平面應變狀態時對應軸對稱拉伸（ η=1/3）或等雙軸壓縮（η=?2/3）；L為Lode參數；θ、=?1時對應軸對稱壓縮（η=?1/3）或等雙軸拉伸（η=2/3）。理論上可以采用參數 (η,L為Lode參數；θ、)描述各向同性材料的任意應力狀態，表1列舉一些典型應力狀態所對應的和η。

表1 一些典型應力狀態所對應的Lode角參數和應力三軸度ηTable 1 Lode angle parameter and stress triaxiality η of some typical stress states

表1 一些典型應力狀態所對應的Lode角參數和應力三軸度ηTable 1 Lode angle parameter and stress triaxiality η of some typical stress states

ˉθ η Principal stress Stress state?1 ?1/3 σ1=σ2=0,σ3=?ˉσ Axial symmetry compression 2/3 σ1=σ2=ˉσ,σ3=0 Equi-biaxial tension 0 ?√3/3 σ1=0,σ2=?√3ˉσ/3,σ2=?2√3ˉσ/3 Plane strain compression 0 σ1=√3ˉσ/3,σ2=0,σ2=?√3ˉσ/3 Pure shear√3/3 σ1=2√3ˉσ/3,σ2=√3ˉσ/3,σ2=0 Plane strain tension 1 1/3 σ1=ˉσ,σ2=σ3=0 Axial symmetry tension?2/3 σ1=0,σ2=σ3=?ˉσ Equi-biaxial compression

1.2.1 應力三軸度

大量研究證明，應力三軸度 η是影響材料損傷斷裂行為的關鍵因素。微觀上，在高 η條件下，材料通常表現為拉伸型斷裂，形核后的空洞在拉應力作用下發生明顯長大并聚合；而在低 η條件下，主要表現為剪切型斷裂，空洞沿最大剪應力方向被拉長，形狀變化明顯但體積變化較小[19-21]。宏觀上，一般認為材料的延性和 η成反比，例如，Kao等[22]與Bridgman[23]的實驗結果以及Rice等[18]、Mcclintock[24]的理論分析都表明等效斷裂應變隨著 η的增加而減少；但是近年來的研究發現并不是 η的單調遞減函數，例如Al2024-T351鋁合金[17]、1045鋼[23]、4340鋼[25]的實驗結果表明純剪切（η=0）變形時的εˉf比單軸拉伸（η =1/3）時要低。Bao等[17]對Al2024-T351鋁合金開展了一系列的斷裂實驗研究，構建了圖3所示的二維斷裂軌跡圖，首次揭示了大 η范圍內金屬材料和η 的非單調關系；在拉應力起主導作用的變形模式下，存在一個 η≈0.4的不連續的極值點，當 0 <η<0.4， 隨著 η的增大，例如從純剪切變形過渡到單向拉伸變形，材料的明顯增大；而當η<0 或 η >0.4時 ，隨 η增大而單調下降。

此外，圖3還表明，存在一個材料不發生斷裂的應力三軸度截斷值（=?1/3），當 η <，可認為材料不會斷裂。Lou等[15]認為，當 η<0時，空洞在高的壓應力作用下發生閉合，進而修復了變形過程中的損傷；當 η足夠小時，空洞閉合可抵消了空洞的形核、長大和聚合所造成的損傷累積，從而使得材料不發生斷裂。然而Khan等[26-27]對Al2024-T351鋁合金的實驗研究發現，在非比例雙軸壓縮變形條件（η=?0.496）下，該材料亦出現了破裂現象。因此，并不存在一個統一的，僅采用應力三軸度亦不能完全描述應力狀態對材料斷裂行為的影響。

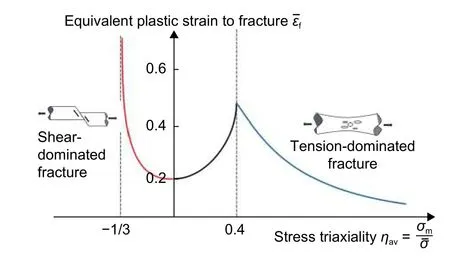
圖3 等效塑性斷裂應變與平均應力三軸度的關系Fig. 3 Relationship between equivalent strain to fracture and average stress triaxiality

1.2.2 Lode角參數的影響

研究發現，偏應力狀態和剪切效應同樣顯著影響金屬的斷裂行為，特別是在低η 的變形模式下，金屬材料的斷裂機制主要為局部剪切失效和剪切帶的形成[14，17]。其中，Lode角是描述剪切效應的關鍵參數[9，28]；在低 η條件下，Lode角參數對微空洞的變形有重要影響，特別是斷口附近的空洞；在高η下，對于中等強度和加工硬化金屬，Lode參數對斷裂應變的影響不太明顯[29-30]。

關于金屬材料的韌性斷裂行為，目前已基本達成共識，需同時考慮應力三軸度和Lode角參數的影響，以可靠描述材料在多軸復雜應力狀態下的斷裂行為。

2 非耦合韌性斷裂準則

非耦合型斷裂準則通常采用等效斷裂應變描述材料的延性，并將其表示為應力狀態的函數，結合具體塑性本構理論實現延性材料的斷裂預測。

2.1 傳統的非耦合型模型

傳統的非耦合模型一般為經驗模型，采用應力相關的權函數描述塑性變形累積導致的斷裂行為，因此也稱為基于應力的斷裂準則，其統一的表達式如下：

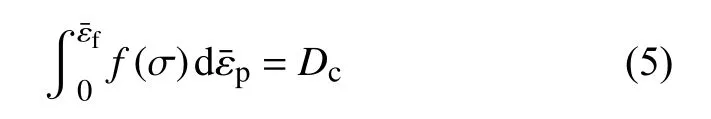
式中：f(σ)為 應力狀態相關的權函數；為臨界斷裂應變；Dc為無量綱的斷裂損傷閾值。當左側積分項達到Dc時，認為材料發生韌性斷裂，此時對應的等效塑性應變即為。顯然，具體的斷裂準則取決f(σ)的形式，表2為典型非耦合斷裂準則及其適用場合（）。

表2 傳統的非耦合韌性斷裂準則及其應力三軸度截斷值（?η）Table 2 Traditional uncoupled ductile fracture criteria and their cutoff of stress triaxiality

對金屬材料斷裂行為的預測可以追溯到20世紀50年代，Freudenthal[31]采用塑性功描述材料損傷斷裂行為，提出了第一個韌性斷裂準則。Cockcroft等[32]基于拉伸和扭轉實驗結果，提出了經典的Cockcroft-Latham（C-L）準則，認為最大主應力 σ1是導致材料破壞的主要因素，即最大拉應力加權修正后的累積等效應變達到時，材料發生斷裂。1972年，Brozzo等[33]對C-L模型進行修正，引入了平均應力項影響，以預測金屬板材的成形極限。1979年，Oh等[34]在C-L模型上引入等效應力項。C-L模型最初是針對體積成形而建立的，1968年，Tarigopula等[38]證明該模型亦適用于板料成形；該系列模型的共同特征取決于 σ1>0。

Mcclintock[24]通過對圓柱形空洞的長大行為研究提出η 是影響材料斷裂的關鍵參數。1969年，Rice等[18]研究了理想材料中的單個球形空洞在遠場正應力作用下的演化規律，并提出了考慮 η的空洞長大的Rice-Tracey（R-T）模型，給出了空洞長大的幾何描述。1970年，Oyane等[35]基于孔隙材料的壓縮塑性本構關系提出一種考慮平均應力影響的韌性斷裂準則，該準則相當于在McClintock 模型上增加了一個常數項。1985年，Johnson等[36]在R-T 模型的基礎上，提出考慮應變速率與溫度影響的韌性斷裂準則。這些模型的共同特征是認為平均應力是導致材料斷裂的主要因素，因此斷裂準則通常表示為 η的函數。1980年，Wilkins等[37]基于鋁合金的扭轉和拉伸實驗結果，首次提出考慮平均應力和偏應力對材料斷裂行為的影響，不過該模型并未得到廣泛應用。

綜上所述，傳統斷裂準則的權函數f(σ)通常為最大拉應力或平均應力的簡單函數，忽略了偏應力張量對斷裂行為的影響，所確定的斷裂軌跡為二維的，并不適合于在低應力三軸度或復雜應力狀態下的斷裂行為預測，而且Wierzbick等[39]的研究也表明僅使用和 η的二維曲線來表征材料的韌性斷裂性能是不充分的；但這些準則的模型參數較少，實驗標定簡單，因此廣泛用于解決各類工程問題。虞松等[40]通過拉伸、剪切、壓縮和扭轉等實驗分析比較了11種韌性斷裂準則，指出C-L準則和Brozzo準則適用于預測材料在高 η下的成形極限，而R-T準則適用于預測材料在 η下的成形極限。Ben等[41]通過Erichsen 杯凸實驗和有限元模擬，研究了R-T、Oh、Brozzo和Ayada四種斷裂準則對304L不銹鋼斷裂行為的預測精度，其中R-T準則和Brozzo準則均具有較高的預測精度，誤差分別低于4%和6%。總體上，這些傳統斷裂模型大多得到時間的充分證明，在各自適用的場合發揮積極的作用。

2.2 現代非耦合型模型

傳統的非耦合型斷裂準則在金屬成形等 η較低的場合表現不佳。長期以來，有關J3對金屬斷裂行為影響的研究較少，直到Xue[42]、Xue等[28]啟發式地指出Lode角參數也是影響材料斷裂失效的重要參數。此后，Bai等[43]提出了同時考慮σm和Lode角參數的韌性斷裂準則。Beissel等[44]在Johnson-Cook模型中引入J3的影響，考慮拉伸和壓縮強度差異的影響。學界已基本達成共識，即同時與 η和Lode角參數有關。近年來所提出的韌性斷裂準則的共同特征是在 空間內構建材料三維斷裂曲面[43]，而不再局限于高η 的場合。

2.2.1 Bao-Wierzbicki和Xue-Wierzbicki模型

Bao等[17]通過大量的實驗研究發現鋁合金的不是 η的 單調遞減函數，而是高度非線性的。η對損傷斷裂的影響可以分為三個區域：η較大時，斷裂機理主要為空洞長大和聚合； η<0時，剪切型斷裂起主導作用，截斷值為 η=?1/3；η較小時，斷裂由剪切和空洞演化共同決定。Xue等[28]在Bao-Wierzbicki模型的基礎上引入J3的影響，提出了一個考慮Lode角參數的三維對稱斷裂準則，將表示為 (η,ξ)的函數，即：

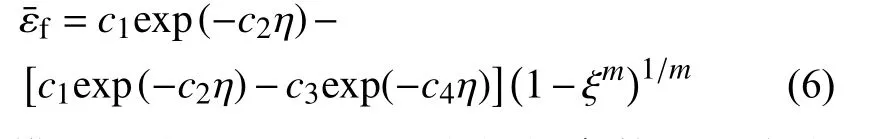
該模型含有c1～c4和m五 個材料參數，η為應力三軸度，ξ為歸一化第三應力張量不變量。采用RT 模型分別描述下限（平面應變條件）和上限（單軸對稱變形）情況下的斷裂軌跡，并采用對稱的非二次橢圓函數描述J3對中間變形狀態的影響。Wierzbicki等[39]基于Al2024-T351的斷裂實驗數據，對比研究了七種韌性斷裂準則的預測性能，指出該模型可以較好地預測材料在較大應力狀態范圍內的斷裂應變。

2.2.2 改進的Mohr-Coulomb（MMC）斷裂準則

經典的Mohr-Coulomb（M-C）準則同時考慮剪應力和正應力對材料失效的影響，廣泛用于巖土的失效預測，其形式如下：

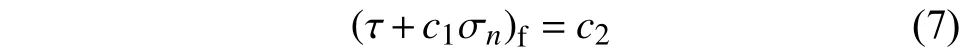
式中：τ和 σn分別為斷裂面上的剪應力和正應力；摩擦系數c1描 述剪應力和正應力的相對權重；c2為剪切阻力。因此，M-C準則可視為最大剪應力準則的擴展，可同時描述正應力和剪應力導致的斷裂行為。

Bai等[12]提出了改進的（Modified）M-C（MMC）準則，將式(7)變換成關于的函數，并提出了一種與Lode角和平均應力相關的材料硬化模型[43]，基于該硬化模型，MMC準則可進一步表示為的函數，如下式所示：

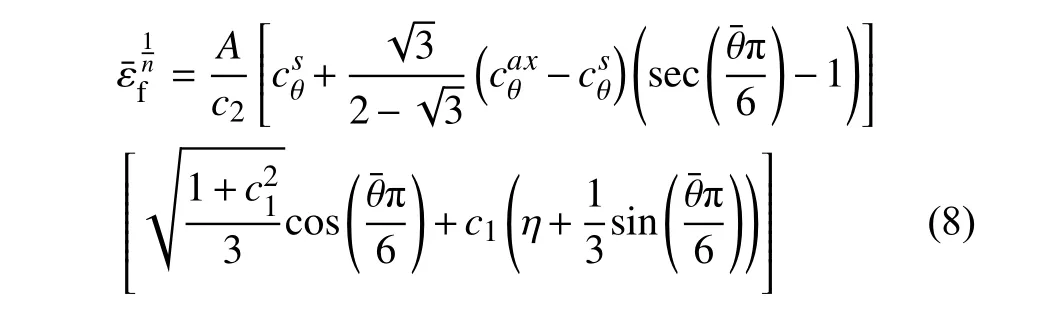
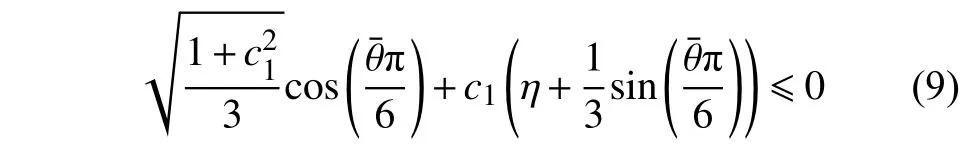
因此，上述截斷區域僅受參數c1的影響。

近年來，MMC準則在結構金屬中的適用性和可靠性得到廣泛的驗證，用于預測了低碳鋼[45]、先進高強鋼[46]、鋁合金[47-48]、鎂合金[49]和高強低合金管材[50]等在不同變形路徑下的斷裂行為。Beese等[51]耦合MMC斷裂準則和Hill48屈服函數研究塑性各向異性對Al6061-T6薄板斷裂行為的影響，其結果表明考慮材料塑性各向異性可提高斷裂預測精度。此外，Luo等[52]仍然以各向同性的MMC準則作為權函數，通過對塑性應變增量 dεp進行線性轉變來得到各向異性斷裂應變增量，從而考慮了塑性各向異性的影響。

Jia等[49]在MMC模型的基礎上進一步建立平面應力條件下的全應變形式的MMC準則，即eMMC，將斷裂應變表示為應變比 α或 φ角（斷裂成形極限圖中與 ε2軸的夾角，如圖4所示）的函數。eMMC模型的優點是應變比 α和 φ角可以通過數字圖像相關法（DIC）實驗獲得，因此在研究材料的斷裂行為時可以排除塑性非線性行為的影響，特別是對于具有復雜塑性變形行為的材料具有明顯優勢。作者采用該準則預測了TRIP780鋼板和AZ31BH24鎂合金板在不同加載條件下的斷裂行為，具有較好的準確性。

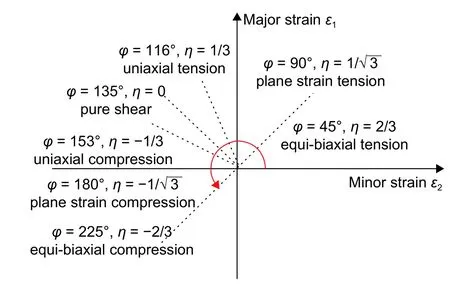
圖4 比例加載條件下斷裂成形極限圖中的φ角示意圖Fig. 4 Schematic FFLD describing the definition of φ under proportional loading condition

2.2.3 基于細觀力學的Hosford-Coulomb 準則

Mohr等[53]采用Hosford等效應力和作用在最大剪切應力平面上的正應力構建了Hosford-Coulomb（H-C）斷裂準則。其具體形式如下：

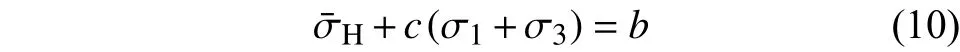
其中，

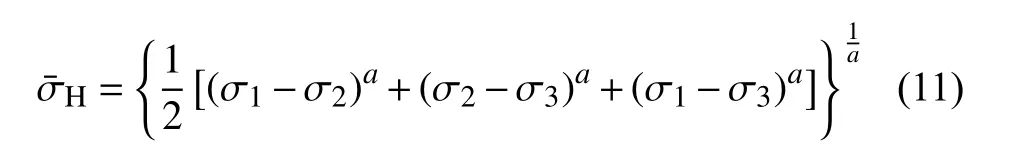
顯然，當a=1時，H-C模型退化為Mohr-Coulomb 模型，因此該準則可視為擴展的Mohr-Coulomb準則。根據最大主應力與 η和Lode角參數之間的關系，可將式（10）轉變至的空間，即：

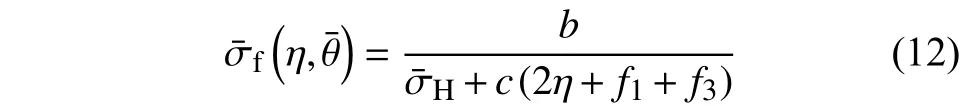
H-C準則與MMC準則具有相似的理論背景；但在雙軸拉伸變形條件下，由于M-C模型與第二主應力σ2無關，因此退化為最大主應力準則，而H-C模型同時考慮了三個主應力分量的影響，因此對雙軸應力比 σ2/σ1敏感。此外，這兩個準則采用不同的硬化模型將等效應力轉換為等效應變；MMC采用的是Lode角參數和平均應力相關的本構模型，而H-C準則則使用了各向同性的硬化準則，前者稱為非一致模型而后者稱為一致模型[53]。在一致模型中，使用等效應力與等效應變預測的結果一致，而在不一致模型中，等效應力與等效應變的預測結果不一致。Pack等[54-55]的研究表明，Lode角參數和應力三軸度相關的H-C模型不僅能夠預測試塊實驗中起裂的瞬間和位置，還能夠預測復雜的結構問題。

2.2.4 Magnitude-Stress-Vector（MSV）準則

Khan等[27]發現，Al2024-T351鋁合金在η

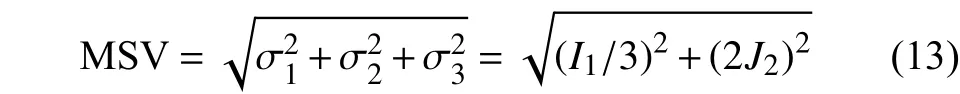
也可以表達成應力張量第一不變量的函數形式：

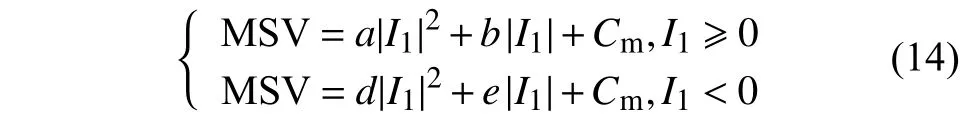
式中：a,b,d,e和Cm是需要標定的材料參數。

在隨后的工作中，Khan等[26]將MSV準則進一步發展成為包含應變速率和溫度的形式，修改后的MSV準則可以考慮應變速率和溫度對韌性斷裂的影響。

2.2.5 Lou-Huh系列韌性準則

Lou等[15]基于韌性斷裂的微觀機制，即空洞的形核、長大以及沿最大切應力方向的剪切合并，提出了形式簡潔的韌性斷裂判據DF2012，如下式所示：

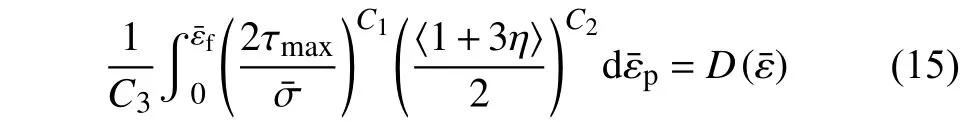
該模型隱式地考慮了塑性變形對空洞形核的主導作用、η對空洞長大的主導作用和最大剪應力τmax對空洞聚合的主導作用。因此DF2012等Lou-Huh系列也被稱作基于物理機理的非耦合韌性斷裂準則。該模型經過DP780[15]、Al2024-T251[15]及DP980[56]等材料的驗證，具有較高的預測精度。

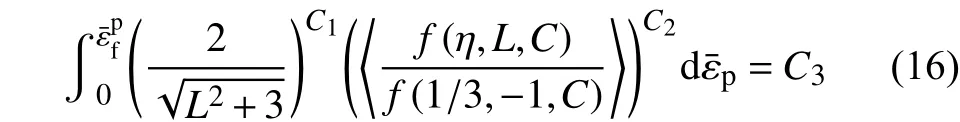
其中：

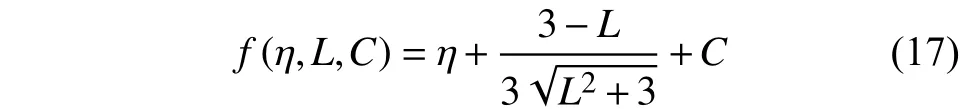
經驗參數C間接描述微觀組織、溫度和應變率等對? η的影響。Lou等[57]基于Al2024-T351的實驗結果并與MSV、MMC準則比較，DF2014準則能夠預測材料在較大范圍變形條件內斷裂行為，例如從雙軸壓縮（η =?0.5）到平面應變拉伸（η=0.6）。

Lou等[58]對DF2014準則進行進一步修正，引入參數C4以描述Lode角參數對空洞扭轉的影響，以更準確描述剪切、單軸拉伸、平面應變拉伸和平衡雙軸拉伸等四種臨界加載條件下的板料斷裂行為。該模型被稱為DF2016，其表達式為：

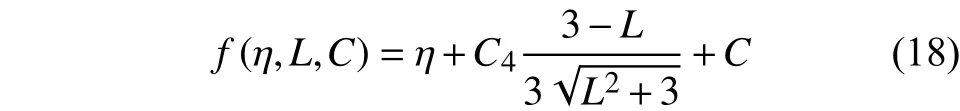
當C4=1時，DF2016退化為DF2014；當C4=0，C=1/3時，DF2016進一步退化為DF2012。

近年來，這一系列的韌性斷裂準則得到越來越多的關注，其準確性和可靠性得到多種金屬材料的證明，包括 DP980的剪切變形和平面應變拉伸變形[59]，DP780的脹形高度預測[60]等，Al2024-T351非比例加載下的斷裂預測[61]，DP780的邊緣斷裂預測[62]，以及馬氏體鋼在軋制過程中的斷裂行為[63]。

2.2.6 考慮各向異性行為的非耦合的斷裂準則

金屬板料在材料制備和熱機械處理過程中通常會形成具有擇優取向的微觀組織，其力學性能具有方向性，因此其塑性變形和損傷斷裂均存在各向異性。考慮各向異性行為的斷裂準則可分為以下三種組合：（1）各向異性屈服函數與各向同性斷裂準則；（2）各向同性屈服函數與各向異性斷裂準則；（3）各向異性屈服函數與各向異性斷裂準則。當前，關于第一種組合的研究成果相對較多。

非耦合斷裂準則并非專門設計以預測材料的各向異性斷裂行為，鑒于各向異性塑性行為對材料變形和損傷斷裂的顯著影響，近年來，許多研究工作者通過線性變換的方式將各向同性斷裂準則擴展為各向異性[49，64-65]。例如Lou等[64]在DF2014斷裂準則的基礎上，通過線性變換將各向同性的塑性應變增量張量轉變為各向異性的損傷等效應變增量得到適用于各向異性的韌性斷裂準則，即：

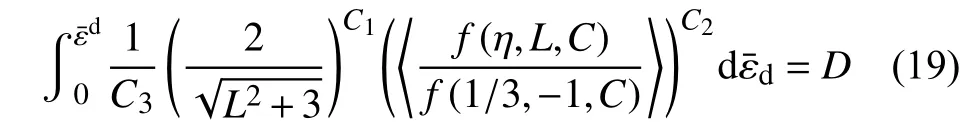
該各向異性DF2014準則中共有13個材料參數，除了DF2014中的4個斷裂參數，還包括額外的9個參數以構建與之間線性轉化矩陣[64]。與實驗數據對比表明，該模型能夠預測沿著RD、DD和TD方向的剪切、單軸拉伸、平面應變拉伸和等雙軸拉伸的韌性斷裂行為[64]。此外，Lou等[65]還通過引入各向異性塑性行為到DF2016中來預測金屬中的韌性斷裂行為，如下式所示：

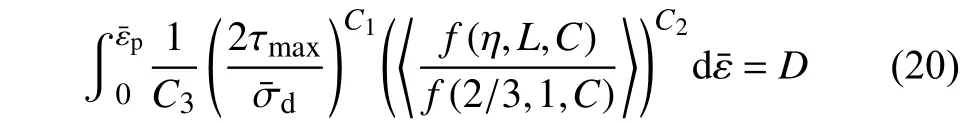
同樣地，Gu等[67]通過應力張量的線性變換，得到了H-C斷裂準則的各向異性的擴展形式。這些模型需要多達9個附加常數來考慮所有三個方向的加載條件。校準這些常數需要大量的實驗數據，這是不切實際的。

總體上，有關非耦合型韌性斷裂準則的研究方興未艾，除了上述列舉論文的斷裂準則外，近年來國內外學者不斷地研究出新的非耦合韌性斷裂準則，包括純經驗的唯象模型[68-71]和基于損傷微觀機制的模型[72]。

2.3 斷裂參數的標定

斷裂準則的可靠性還取決于材料參數標定的準確性。斷裂實驗是校準材料參數的主要方法，例如板材的缺口拉伸實驗、雙軸拉伸實驗、含中心圓孔的單向拉伸實驗、剪切實驗；厚板的平面應變拉伸、彎曲實驗；棒材的缺口拉伸實驗、不同壓縮比的壓縮實驗等[56，61，73-76]。對于唯象的損傷斷裂準則，關鍵的斷裂參數主要有臨界等效斷裂應變、應力三軸度 η和Lode角參數，采用實驗手段直接測量上述參數仍存在較大的挑戰性，DIC實驗技術是目前測量臨界斷裂應變的主流方法，但目前仍很難直接測量 η和Lode角參數，對應力相關變量的測量主要還是借助實驗、理論計算或與數值模擬相結合的方法[56，73]。

由于金屬材料在發生韌性斷裂前會經歷明顯的塑性變形，因此準確可靠的彈塑性本構模型是開展數值的關鍵。盡管von Mises屈服函數和Hill48屈服函數被廣泛用于描述金屬材料的塑性行為；但新的各向異性屈服函數亦逐漸用于描述先進金屬材料的塑性行為。Ha等[73]對Al6111鋁合金板在不同變形路徑下的實驗和模擬研究表明：Yld2004-18p對斷裂區域的變形預測精度高于von Mises屈服函數，基于Yld2004-18p模型的斷裂預測結果更接近于實驗結果。最近，Habib等[74]采用考慮孿晶作用的晶體塑性有限元（CPFEM）模擬鎂合金ZEK100頸縮區域和剪切區域的變形和應力狀態，結果表明這些裂紋萌生區域具有很高的孿晶體積分數，耦合CPFEM和各向異性的H-C斷裂準則能可靠地預測該材料的斷裂行為。因此，盡管非耦合型斷裂準則不考慮損傷對塑性變形的影響，但塑性本構模型的選擇非常關鍵，所以對斷裂模型的標定也包括對本構模型的參數標定。

3 非耦合韌性斷裂準則在航空材料中的應用

近20年來，有關金屬結構材料斷裂行為的研究得到長足發展，相關理論成果和斷裂準則不斷涌現，本節僅論述非耦合型韌性斷裂準則在上述航空材料中的典型應用。

3.1 鋁合金

鋁合金以其優異的成形性能和服役性能，廣泛用于航空、航天和汽車等領域；鋁合金斷裂行為的研究也相對更充分，其中非耦合斷裂準則在2000系、6000系和5000系等變形鋁合金中均得到廣泛應用和驗證，并建立了較完備的斷裂參數數據庫。例如，以鋁合金Al2024-T351為例，美國麻省理工的Bao團隊[17，77]經過近十年系統研究該材料在各種應力狀態下的斷裂行為，原創性地設計了多種實驗樣品規范，研究應力三軸度 η和Lode角參數L的影響，構建了該材料在三維空間內的斷裂面，并先后提出了多個具有代表性的非耦合韌性斷裂準則，包括前述的Bao-Wierzbicki[17]、Xue-Wierzbickit[28]和MMC[12]等。值得一提的是，Wierzbicki等獲得的Al2024-T351鋁合金斷裂實驗數據常被研究人員用作基準實驗數據以檢驗其所提出的斷裂準則[17]。此后，Khan等[27]對Al2024-T351開展了包含純扭轉、拉扭及雙軸壓縮的補充實驗，擴大了實驗的應力三軸度范圍。

傳統的韌性斷裂準則由于其參數較少而極其依賴于標定模型所使用實驗的類型。Hossen等[78]分別采用Ayada、Rice-Tracey和Cockroft-Latham三種斷裂準則預測Al6061鋁合金板在U形彎曲工藝中的斷裂行為，通過單軸拉伸、平面應變拉伸和缺口試樣拉伸實驗標定模型參數，其研究結果表明，斷裂準則及所選擇的標定實驗顯著影響臨界損傷值、斷裂軌跡及斷裂預測精度，其斷裂預測偏差如圖5所示。Martins等[79]基于McClintock損傷模型，結合Hill48屈服函數，分別建立拉伸型斷裂、面內剪切斷裂和面外剪切斷裂的解析模型，預測鋁合金Al1050-H111板的斷裂成形極限圖，并指出在板料成形中的斷裂是由拉伸型斷裂與面內剪切斷裂相互競爭的結果，而在體積成形中的斷裂則是拉伸型斷裂與面外剪切斷裂相互競爭的結果。

Beese等[51]采用了Hill48屈服函數聯合各向同性的MMC準則來描述Al6061-T6鋁合金的各向異性與韌性斷裂行為。Luo等[65]采用實驗與數值模擬相結合的方法研究了Al6061-T6擠壓過程中的各向異性韌性斷裂行為，基于MMC準則通過對等效塑性應變增量進行線性變換來得到各向異性的應變增量，從而考慮了材料塑性各向異性對斷裂的影響。Qian等[47]對承受剪切-壓縮聯合載荷作用下的Al6060-T6保險杠開展實驗與數值模擬研究，結果表明，基于Yld2000-3D屈服函數[80]和MMC斷裂準則的本構模型能準確預測全局載荷-位移響應以及多個的斷裂起始點。Gorji[81]利用Yld2000-3D屈服函數[80]構建的本構模型和H-C韌性斷裂準則來預測鋁合金Al6016-T4盒形件在拉深過程中的斷裂，模擬與實驗結果證明了該本構與斷裂模型的可靠性。Qian等[48]采用非關聯本構模型與MMC韌性斷裂準則預測鋁合金Al5083-O的斷裂行為，結果表明，該模型可同時預測該材料的拉伸型斷裂和剪切型斷裂。

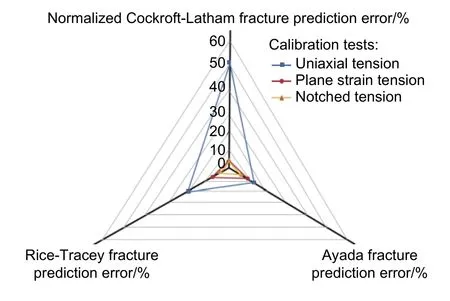
圖5 不同加載條件下，三種斷裂準則預測的斷裂位移的誤差Fig. 5 Errors of the fracture displacements predicted by three uncoupled fracture criteria for different loading conditions.

3.2 鎂合金

作為實際應用中最輕的金屬結構材料，鎂合金具有較高的比強度和廣闊的應用前景，是傳統合金鋼和鋁合金的重要替代材料[82-83]。因其密排六方（HCP）晶體結構，目前對鎂合金塑性變形行為和斷裂失效機制的研究遠不及立方金屬充分，有關斷裂準則在鎂合金中應用的研究也相對較少。鎂合金的塑性成形通常需在200 ℃以上進行[84]，其推廣應用亟待解決的問題是其較差的室溫成形性能。環境溫度下，鎂合金可開動的滑移系較少，主要為基面滑移（提供兩個獨立的滑移系），無法滿足von Mises變形協調準則要求的5個獨立滑移系。因此，孿晶是鎂合金重要的變形機制，孿晶界作為特殊的大角度晶界為空洞提供額外的形核的位置，導致所謂的孿晶誘導斷裂現象[85-86]。此外，鎂合金表現出明顯的各向異性和拉壓不對稱性，因此對鎂合金斷裂預測的前提是正確描述其塑性變形行為。多集中在AZ31鎂合金和部分稀土鎂合金[87]。Ray等[88]

當前對鎂合金斷裂行為的實驗和理論研究大研究了AZ31和ZEK100板材在單軸拉伸載荷下的韌性斷裂行為，其結果表明，ZEK100易受剪切局部化的影響，且在損傷演化過程中孿晶很活躍。Kondori等[87]研究了鎂合金AZ31在不同下的斷裂行為，其結果表明AZ31B的斷裂應變隨 η的增加而減少，并且隨著η 增大，斷裂機制由孿晶誘導斷裂變為微空洞聚結型斷裂。Kang等[89]通過拉伸實驗和紋理掃描對厚度為2 mm的AZ31板材進行了研究，他們報道了早期分散性縮頸的發展以及材料在沒有任何局部縮頸的情況下突然斷裂的現象。Nguyen等[90]采用Oyane韌性斷裂準則預測鎂合金板在旋轉漸進成形工藝中的韌性斷裂行為，并同時考慮了材料的各向同性硬化和隨動硬化行為。Feng等[91]采用Johnson-Cook斷裂準則模擬AZ31B鎂合金在電磁脹形過程中的斷裂失效行為，考慮了應變速率和溫度對材料塑性變形和斷裂行為的影響。Lee等[92]利用不同的延性斷裂準則，包括三種簡單的各向同性斷裂準則、MMC和eMMC來預測AZ31和ZE10兩種鎂合金的斷裂極限，并且使用了一個新的塑性模型[93]用于分離位錯滑移機械孿晶對斷裂應變的貢獻。在方管壓縮實驗中所有的韌性斷裂準則均可進行合理預測，而三點彎曲實驗中只有MMC能提供較好的失效預測。Ahn等[94]為了預測鎂合金AZ31B板料室溫下的單軸和雙軸加載路徑下的失效行為，提出了一個基于最大剪應力準則的斷裂準則。結果表明，材料的各向異性和不同的加工硬化行為是影響斷裂預測的主要因素。

3.3 鈦合金

對于延性較低的鈦合金，傳統的基于頸縮假設的成形極限圖難以有效預測其韌性斷裂[95]。韌性斷裂準則常用于預測鈦合金成形過程中在剪切、壓縮等具有低、負應力三軸度情況下的失效起始點。Goglio等[96]對Ti-6Al-4V開展了15組力學實驗，通過實驗和數值模擬相結合的方法確定該材料的本構模型參數以及Bao-Wierzbicki模型參數，最終獲得良好的預測結果。Ma等[97]研究9種韌性斷裂準則對TA2鈦合金管旋壓過程中損傷演化的預測能力，結果表明：除Freudenthal模型、Rice-Tracey模型和Ayada模型外，其他斷裂準則都可靠預測試樣的損傷分布，其中，C-L準則的預測結果最接近實驗結果。隨后他們又將這些斷裂準則嵌入有限元軟件ABAQUS中，模擬了不同減薄率下Ti-15-3鈦合金管旋壓過程中的損傷演化[98]，結果表明，只有McClintock模型預測斷裂行為和實驗結果一致。

舒瀅等[99]采用6 種韌性斷裂準則預測鈦合金Ti40在高溫下變形下的損傷與斷裂行為。研究結果表明，只有Oyane準則能可靠預測該合金的斷裂與損傷行為；隨后，他們引入了Zener-Hollomon因子（Z參數）以描述變形溫度和應變速率對等效斷裂應變的影響[100]，結果表明與 lnZ呈線性關系。張士宏等[101]基于連續損傷理論，引入Z參數相關的修正函數 A(Z)，建立TC11 鈦合金高溫塑性變形的損傷演化模型，通過高溫單軸拉伸實驗確定了模型系數。

鈦合金作為典型的HCP金屬，和鎂合金類似，其塑性行為明顯不同于立方金屬[102-103]。Khan等[26]通過分析平均壓力對Ti-6Al-4V各向異性韌性斷裂行為的影響，提出了一種新的非耦合各向異性韌性斷裂準則。為了充分考慮Ti-6Al-4V合金的各向異性和拉壓不對稱性，針對性地提出了改進的Hill各向異性屈服函數、標定該材料的KHL硬化模型參數；所建立的本構理論能預測Ti-6Al-4V在不同溫度與應變速率下的失效行為，其預測結果與實驗結果吻合度很高。

綜上所述，綜合考慮應力三軸度與Lode角參數的非耦合韌性斷裂準則能可靠預測拉伸型斷裂與剪切型斷裂。諸如MMC、H-C、Lou-Huh系列等斷裂準則被廣泛應用于復雜塑性成形工藝中，如盒形件拉深成形、U形彎曲和鋁型材擠壓等。而傳統的非耦合韌性斷裂準則無法預測材料在大應力三軸度范圍內斷裂行為，適用于簡單的變形模式和特定的成形工藝。當前，有關鋁合金的斷裂行為的研究較為充分，相關的實驗數據涉及廣泛的應力狀態范圍和不同的變形模式，極大便利了針對鋁合金斷裂準則的參數標定與擬合。相比于鋁合金，非耦合韌性斷裂準則在鎂合金、鈦合金中應用有限，這與對它們塑性變形和損傷斷裂機制的認識尚不成熟有關；而有關斷裂準則在鎂、鈦合金的應用也多集中于傳統模型上，針對具體工藝條件進行分析，選擇合理的韌性斷裂準則，對鎂、鈦合金的斷裂預測至關重要。表3針對鋁、鎂、鈦合金列舉幾種工藝的韌性斷裂準則的選擇方案，供讀者參考。

表3 鋁合金、鎂合金和鈦合金在特定成形工藝條件下適用的非耦合韌性斷裂準則Table 3 Uncoupled ductile fracture criteria for aluminum alloy，magnesium alloy，and titanium alloy under specific forming conditions

4 結束語

非耦合韌性斷裂準則發展至今已有70余年的歷史，從簡單地只考慮最大主應力或平均應力對韌性斷裂的影響至綜合考慮應力三軸度與羅德角參數的影響，從單位體積塑性功至多孔材料模型、連續介質損傷模型以及在斷裂微觀機理與宏觀力學變量之間建立橋梁的非耦合韌性斷裂準則，從形式與內容上均有顯著發展進步。未來，隨著我國航空、航天工業的迅猛發展，對輕質、高強先進金屬材料的需求日益增加，傳統的成型極限理論難以可靠地預測這些先進金屬材料的成形性能，結合數值模擬和韌性斷裂準則是預測結構金屬損傷斷裂、可成形性以及制定成形工藝方案的重要方法之一，韌性斷裂準則也將隨需求而不斷發展。本文就非耦合韌性斷裂準則的發展趨勢與未來研究方向進行歸納：

（1）研究先進結構金屬材料在復雜變形條件下的損傷斷裂行為，增強其普適性。金屬材料的損傷斷裂一方面受應力狀態和變形路徑的影響，另一方面受微觀組織和失效機制的作用。先進的韌性斷裂模型不僅要充分反映損傷演化的微觀機制，而且要能準確描述不同應力狀態下的影響。現代非耦合韌性斷裂準則的發展主流仍是基于損傷斷裂的微觀機理，引入新的變量和材料參數分別描述正應力和剪應力對損傷演化的影響，覆蓋越來越廣的應力狀態，具有更好的普適性。因此，當前韌性斷裂準則的典型特征是綜合考慮應力三軸度與Lode角參數的影響，構建材料的三維斷裂軌跡。此外，考慮溫度與變形速率的韌性斷裂準則對熱成形和溫度與應變速率敏感的材料至關重要。綜合考慮復雜應力狀態、多種損傷機制和各向異性行為的非耦合韌性斷裂準則需要更多的材料參數，準確可靠地標定先進斷裂準則的材料參數是一大挑戰；常用的實驗標定技術大多是比例加載，那么在復雜加載路徑、非比例加載情和反向加載等情況下的適用性有待商榷。

（2）增強非耦合韌性斷裂準則對強各向異性材料的預測能力。以鋁合金、鎂合金、鈦合金和先進高強鋼為代表的輕質高強結構金屬通常具有明顯的各向異性，而無論以各向同性屈服函數與各向同性斷裂準則或以各向異性屈服函數與各向同性斷裂準則為組合的本構模型，均會存在偏差，發展各向異性損傷斷裂準則和模型是提高預測精度的有效途徑。

（3）建立多尺度、基于物理機理的韌性斷裂準則。韌性斷裂準則在傳統鋼鐵材料中得到較為廣泛的應用，但在鋁合金、鎂合金和鈦合金等材料中的應用則相對較少。特別是密排六方晶體結構的鎂合金和鈦合金等，變形行為更復雜、延展性和成形性能有限，這為韌性斷裂準則的研究提出了新的挑戰。對于這類變形機制和損傷行為復雜的金屬材料，建立多尺度的、基于物理機理的韌性斷裂準則也是未來發展方向之一。總之，針對先進結構金屬材料，在當前研究工作的基礎上，建立綜合考慮塑性變形和損傷演化微觀機制、宏觀應力狀態、應變路徑和工藝參數等因素的韌性斷裂預測模型，將為高性能航空構件的成形工藝設計與優化以及零部件在極端服役環境下的失效行為研究提供可靠的理論指導。

（4）厘清微觀損傷機理與宏觀力學變量之間的聯系，科學搭建微觀-宏觀橋梁。基于空洞形核、長大與合并微觀機理的非耦合韌性斷裂準則仍然是在一些缺乏可靠認證的猜想與假設的基礎上進行的，科學建立微觀-宏觀映射機制，為非耦合韌性斷裂準則發展奠定堅實科學基礎。