THE EXISTENCE AND STABILITY OF STATIONARY SOLUTIONS OF THE INFLOW PROBLEM FOR FULL COMPRESSIBLE NAVIER-STOKES-POISSON SYSTEM?
Hakho HONG
Institute of Mathematics,State Academy of Sciences,Pyongyang,D P R Korea
E-mail:hhong@amss.ac.cn
Abstract In this paper,we consider an inflow problem for the non-isentropic Navier-Stokes-Poisson system in a half line(0,∞).For the general gas including ideal polytropic gas,we first give some results for the existence of the stationary solution with the aid of center manifold theory on a 4×4 system of autonomous ordinary differential equations.We also show the time asymptotic stability of the stationary solutions with small strength under smallness assumptions on the initial perturbations by using an elementary energy method.
Key words Navier-Stokes-Poisson system;inflow problem;stationary solution;existence;stability
1 Introduction and Main Results
The compressible Navier-Stokes-Poisson (called NSP in the sequel for simplicity) system may be used to simulate the transport of charged particles (e.g.,electrons and ions) under the influence of the electro-static potential force governed by the self-consistent Poisson equation.In this paper,we consider the following unipolar compressible NSP equations in the Eulerian coordinate:

We consider the initial-boundary value (IBV) problem to the system (1.1) on [0,∞) supplemented with the initial data and far field conditions

We are interested in the large-time behavior of solutions for the initial-boundary value problem (1.1)–(1.3) in the case of u>0;that is,the inflow problem.


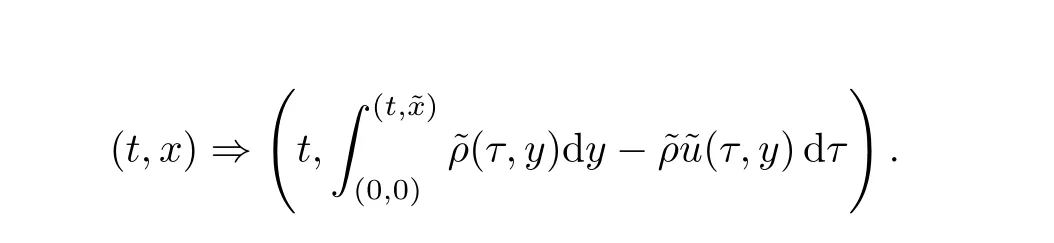
Thus the system (1.1)–(1.3),(1.5) can be transformed into the following moving boundary problem in the Lagrangian coordinates:
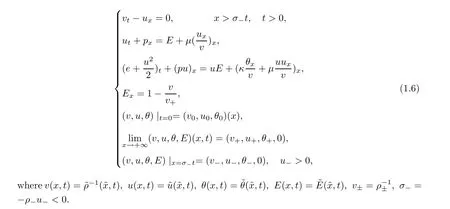
To fix the moving boundary x=σt,if we introduce a new variable ξ=x ?σt,then(1.6) yields the following inflow problem in the half-line:

Setting v=ρ,it is well-known that by using any given two of the five thermodynamical variables(v,p,e,θ and s),the remaining three variables are smooth functions of them,where s is the entropy of the gas.Using the second law of thermodynamics,θds=de+pdv,and (1.4),we can deduce (see [8]) that
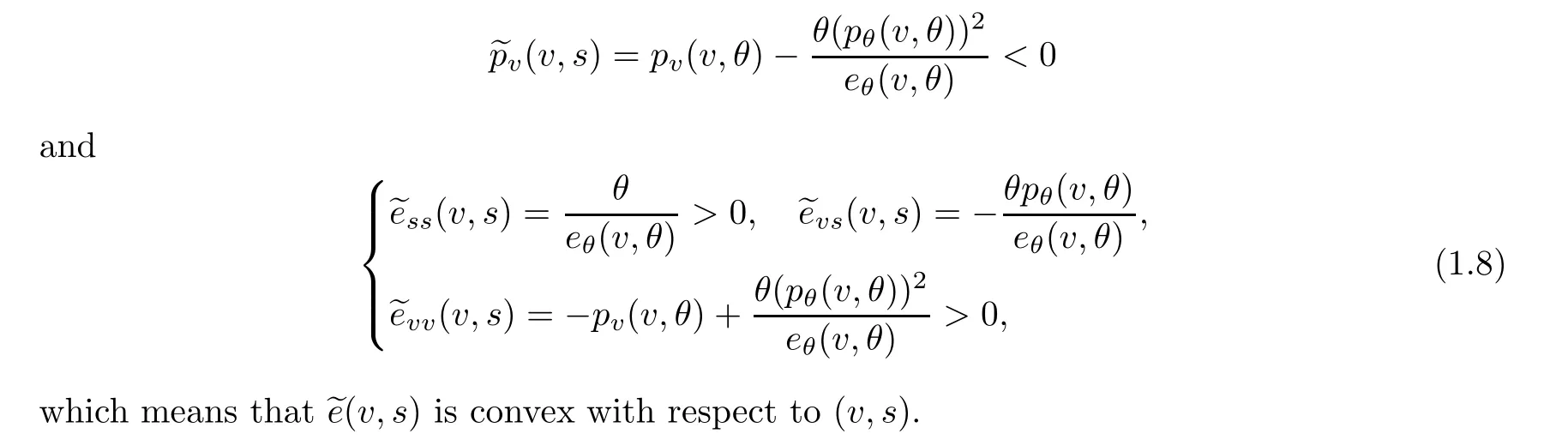


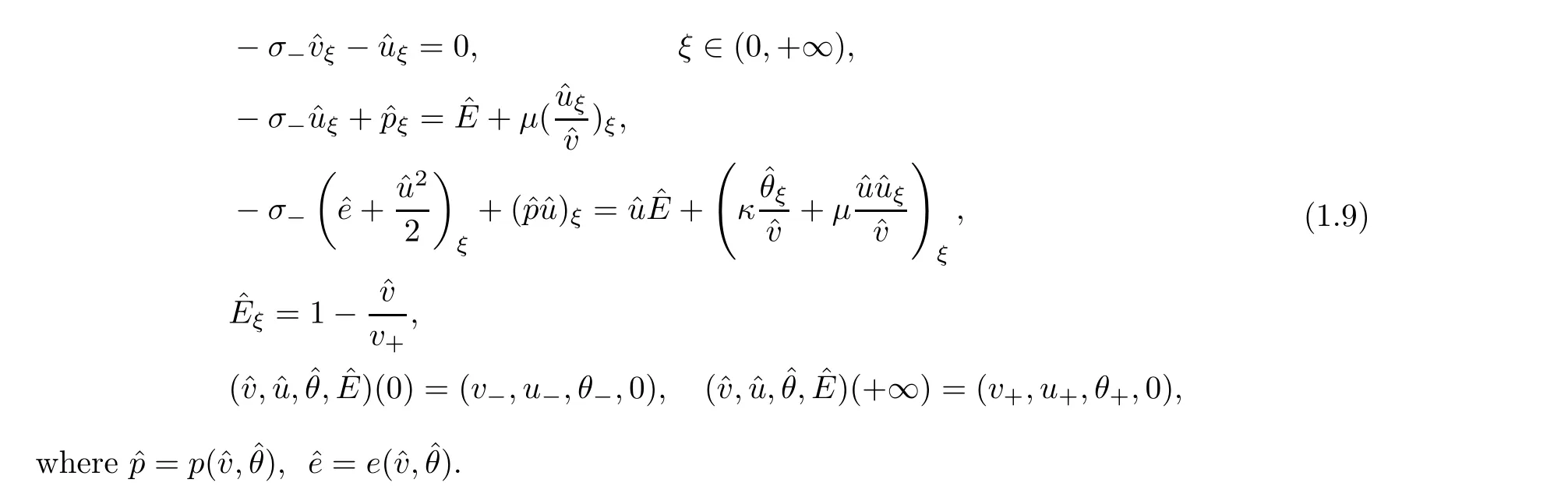
The sound speed and the Mach number are defined by
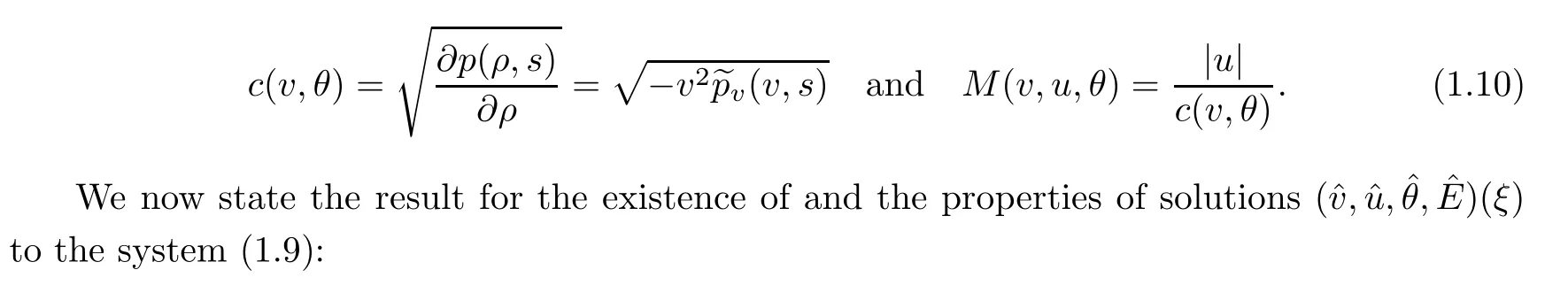
Theorem 1.1
(Existence of stationary solution) Let v>0,u>0,θ>0.The necessary condition for the existence of a solution to system (1.9) is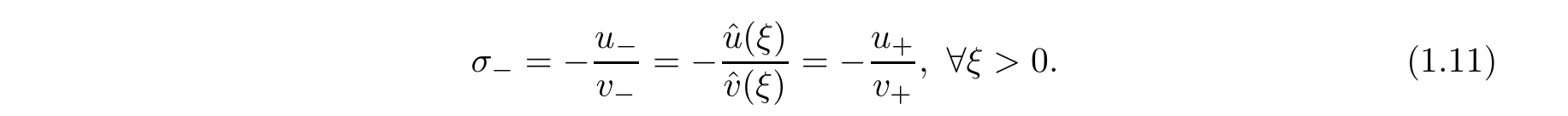
Thus,if u≤0,there is no solution to system (1.9).
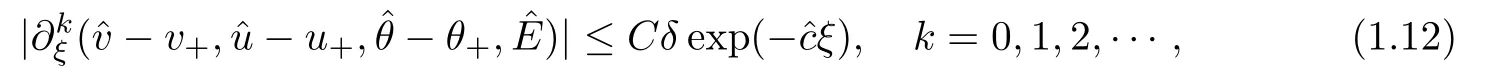
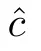

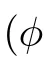
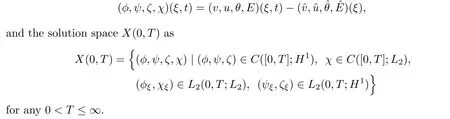
Theorem 1.3
(Asymptotic stability for general gas) Let v>0,u>0,θ>0.Suppose
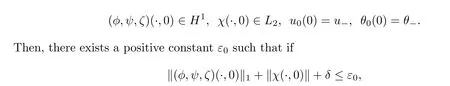
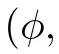

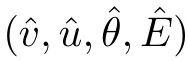
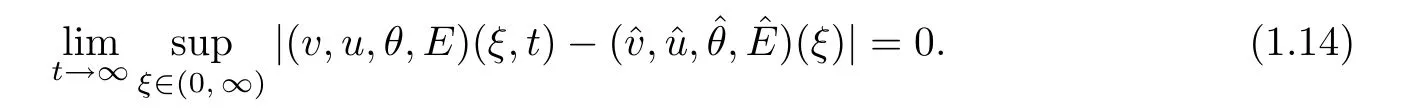
Remark 1.4
Note that the stability analysis in Theorem 1.2 is the first result for the inflow problem of compressible Navier-Stokes-Poisson system in a half line.Also,we’d like to emphasise that the similar stability results can be applied to the case in which there is a combination of the following four basic waves:the 1,the 3-rarefaction waves,the stationary solution and the viscous contact wave;all by arguments similar to those in [17]or [9].That will be left for the future work.Related results
Since the 1990’s,there have been a great number of mathematical studies about the compressible unipolar or bipolar NSP systems in different settings.In what follows,we only mention those related to our interest;that is,the one dimensional problem with different gas states at far fields or at the boundary and the far field.For the Cauchy problem of the bipolar compressible NSP system with the nontrivial electric potential at far fields x=±∞,the stability of rarefaction waves was studied by Duan-Liu [4]and Duan-Liu-Yin-Zhu [5]in the isothermal and non-isentropic cases,respectively.
Also,for the initial-boundary value problem of the bipolar compressible NSP system,the large-time behaviors of the solutions were studied in [2,3,7,13,18,20,21].For the isentropic outflow problem,Duan-Yang [3]proved the stability of the rarefaction wave and stationary solutions,Zhou-Li[21]showed the convergence rate toward stationary solutions and Yin-Zhang-Zhu [20]proved the stability of the superposition of stationary solutions and the rarefaction wave.For the non-isentropic outflow problem of ideal polytropic gas,Cui-Gao-Yin-Zhang [2]proved the stability and convergence rate toward stationary solutions.For the non-isentropic gas-gas free boundary problem of ideal polytropic gas,Liu-Yin-Zhu[13]and Ruan-Yin-Zhu[18]proved the stability of contact discontinuity and the superposition of the rarefaction wave and contact discontinuity,respectively.Recently,for the non-isentropic inflow problem with general pressure law,Hong-Shi-Wang[7]proved the stability of stationary solutions.Here,we’d like to emphasize that the asymptotic profiles of solutions in [2,3,7,13,18,20,21]are the same as those in compressible Navier-Stokes equations.
On the other hand,for the unipolar NSP system with doping profile,Jiang-Lai-Yin-Zhu
[12]and Wang-Zhang-Zhang [19]studied the existence and stability of stationary solutions to the outflow problem of isentropic gas.However,to the best of our knowledge,there is little in the way of results about the stability of nonlinear wave patterns for the inflow problem on the unipolar NSP system with doping profile,which is the subject of our interest in this paper.
Before concluding the introduction,we point out that there are many results on the study of wave patterns to the inflow problem for the compressible Navier-Stokes system;see[6,8–11,14–17]and references therein.For the isentropic Navier-Stokes system,Matsumura-Nishihara[14]established the asymptotic stability of the boundary layer solution and the superposition of the boundary layer solution and the rarefaction wave.Huang-Matsumura-Shi [11]demonstrated the stability of the viscous shock wave and the boundary layer solution.Recently,Fan-Liu-Wang-Zhao [6]proved the stability of the boundary layer solution and the rarefaction wave under large initial perturbations.On the other hand,for the full Navier-Stokes system,Qin-Wang [16]and Nakamura-Nishibata [15]proved the stability of the boundary layer solution in Lagrangian coordinates and Eulerian coordinates,respectively.Later,Huang-Li-Shi [10]demonstrated the stability of the superposition of the rarefaction wave and the boundary layer solution,and Qin-Wang[17]showed the stability of the superposition of 4 waves:the boundary layer solution,1,3-rarefaction waves and contact discontinuity.Recently,Hong-Wang in [8]and [9]generalized the results of [16]and [17]into the case of large initial perturbations.
Here,we outline what is novel in our approach.Compared to the inflow problem of the full Navier-Stokes system,our inflow problem is more general and more complex because the electric field is taken into account.For instance,in order to obtain the existence of stationary solutions,we have to introduce a new variable to deduce the stationary equations to a 4×4 system(2.5)of autonomous ordinary differential equations instead of the 2×2 system required for the full Navier-Stokes equations(see Section 2).Also,in the proof of a priori estimates used to deduce the result desired for the stability of the stationary solutions,we need more delicate non-trivial calculations (see Section 3).
The remainder of this paper is organised as follows:in Section 2,we discuss the existence of the stationary solutions with the aid of the stable manifold theory.Section 3 is devoted to showing the asymptotic stability result of the stationary solutions.
2 Existence of Stationary Solutions
2.1 Reformulation of stationary problem
Integrating the first,second and third equations in (1.9) over [ξ,∞) yields

Letting ξ=0 in (2.1),the first equation yields (1.11).Thus,if u≤0,there is no solution to the system (1.9).
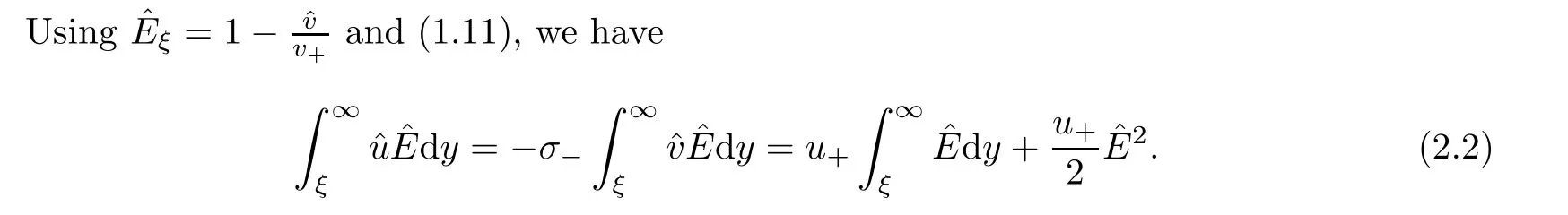

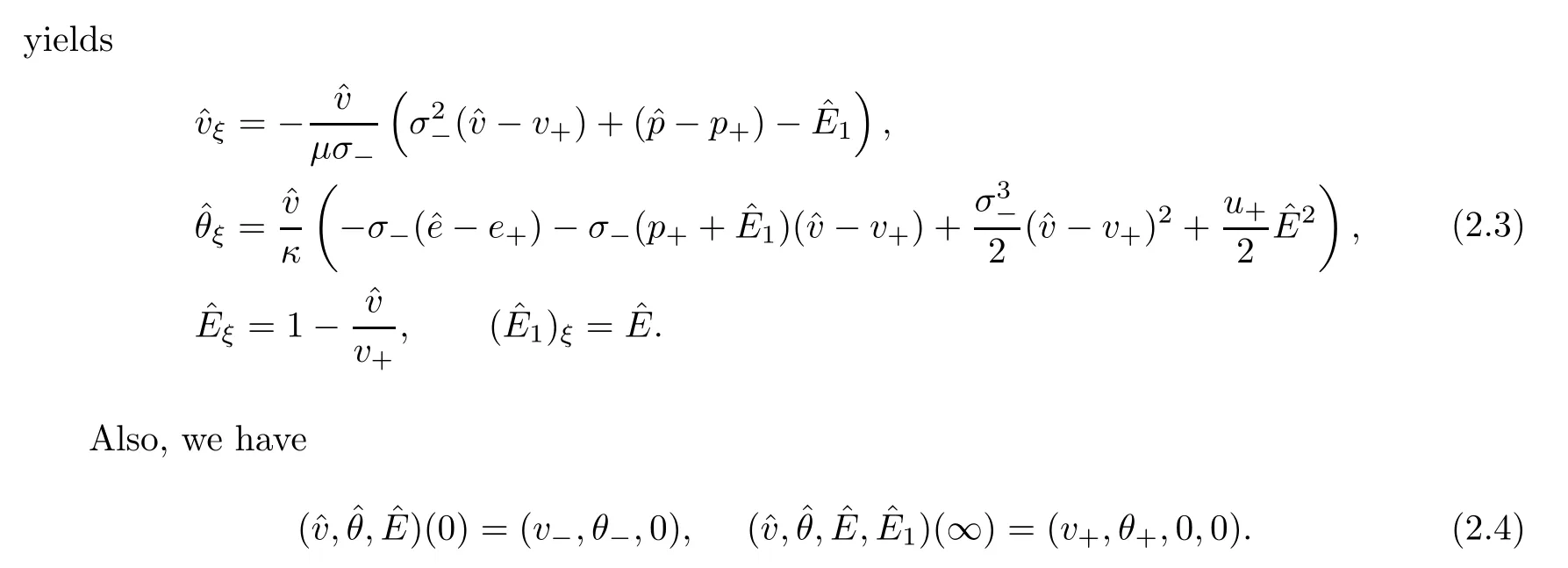
To discuss the solvability of the system (2.3),(2.4) near the infinity asymptotic state(v,θ,0,0),we need to introduce the stationary perturbation variables given by
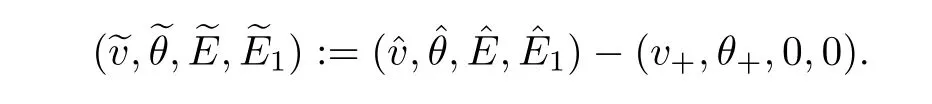

where Jis the Jacobian matrix at an equilibrium point (0,0,0,0) defined by

2.2 Proof of Theorem 1.1


For the case 1) in (2.9),this is impossible,due to (2.12).For the case 2) in (2.9),we must have that a <0,because 2a(λ+λ) <0,λ>0 and λ>0,by (2.12).For the case 4) in(2.9),if a >0(c >0),then c <0(a <0),because,by (2.12),ac <0.Therefore,without the loss of generality,we can assume that
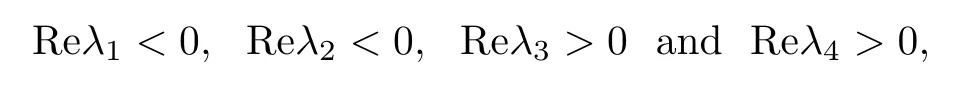
where λ(i=1,2) are real roots or two complex conjugate roots.
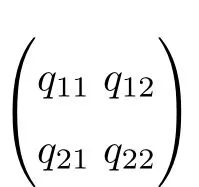
In order to make the manifold theory directly applicable,we need to reduce the system(2.5)to block diagonal form.By the Jordan Theorem from linear algebra,there is a real nonsingular matrix Q=(q)such that

where A is a 2×2 matrix having eigenvalues with a positive real part,and B is a 2×2 matrix having eigenvalues with a negative real part.Therefore,the linear transformation
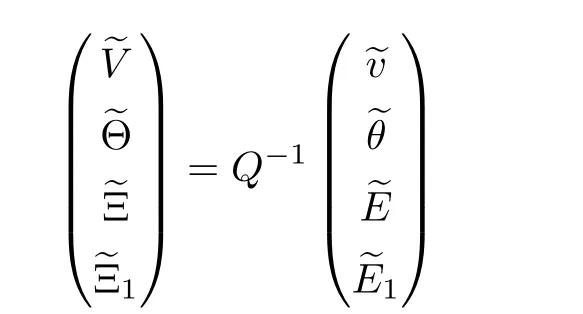
applied to the system (2.5) yields the equivalent boundary value problem

where H(i=1,···,4) are defined by
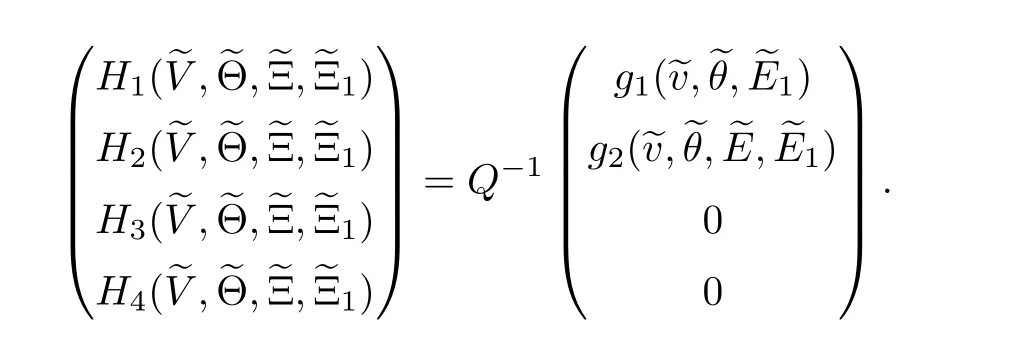
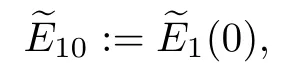
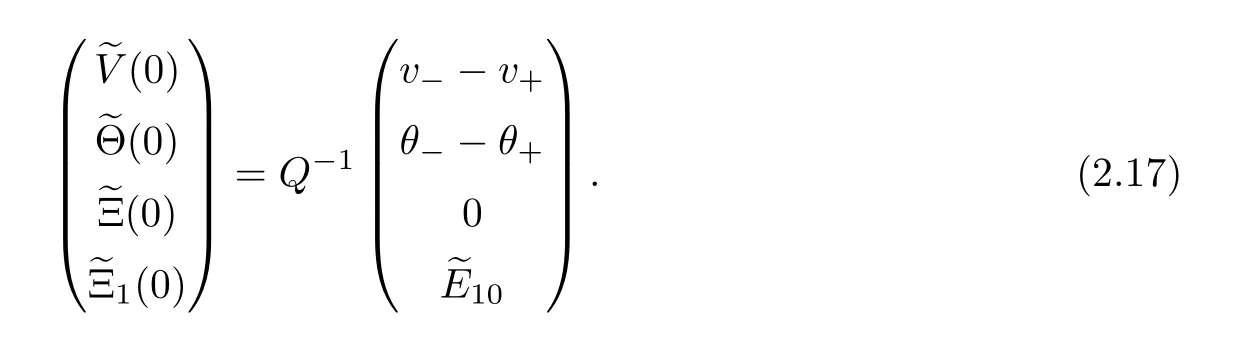
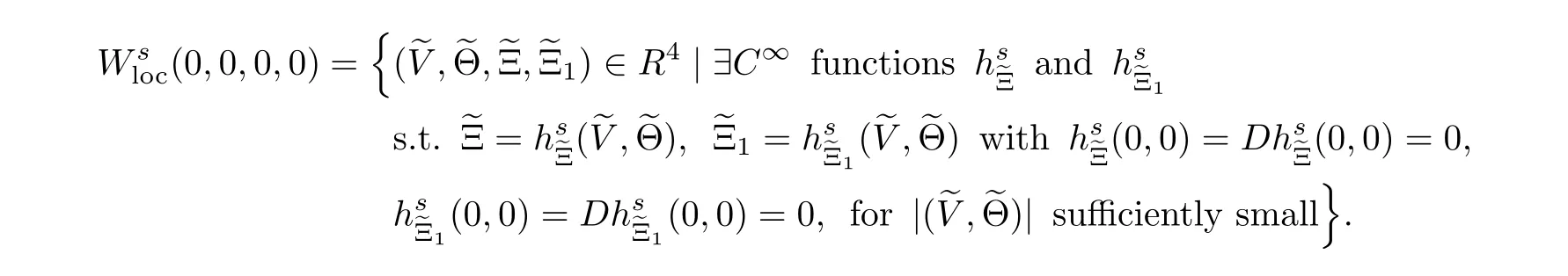
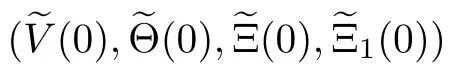
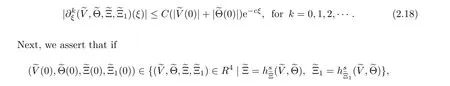
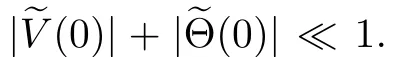

By(2.21),(2.24)and(2.25),we obtain the fact that the vector(q,q,q,q)is parallel to the vector (q,q,q,q),which is impossible,since the matrix Q is nonsingular.Therefore,the matrix ?Q is nonsingular.
Notice that
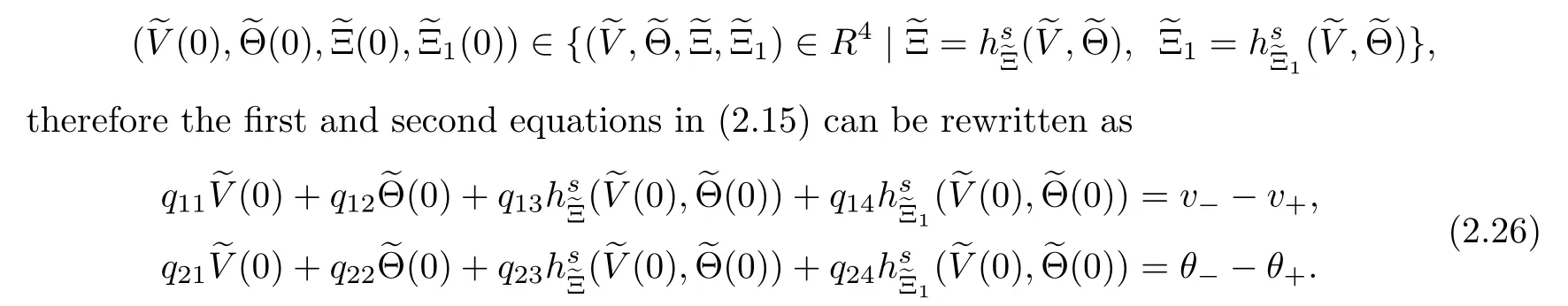

if |v?v|+|θ?θ|?1.This implies that the assertion mentioned at the beginning of this paragraph holds.In addition,from(2.27),it follows that the condition(2.18)is also equivalent to (1.12).By combining the information as above,we complete the proof of Theorem 1.1.
3 Stability of Stationary Solutions

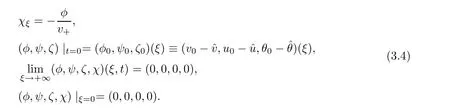
3.1 A priori estimate
To prove Theorem 1.3,a crucial step is to show the following a priori estimate:
Proposition 3.1
(A priori estimate) Besides the assumptions of Theorem 1.3,suppose that (φ,ψ,ζ,χ)∈X(0,T)is the solution to the system (3.4) for some positive constant T >0.Then,there exists a positive constant εsuch that if
Proof
We prove Proposition 3.1 in three steps.Step 1
Energy estimate.
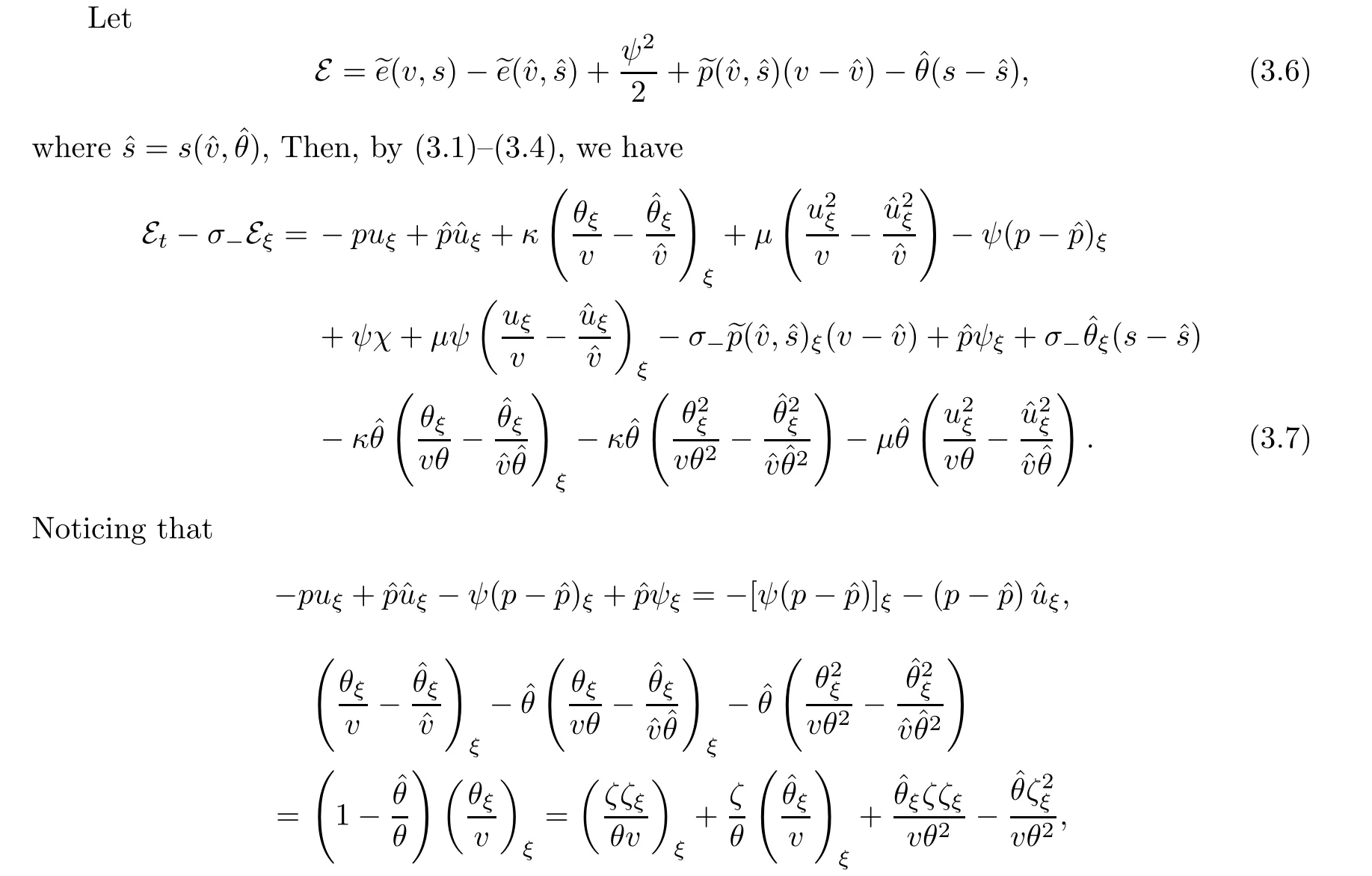



Multiplying the second and third equations of (3.4) by ?ψand ?ζ,respectively,and adding the resulting equalities,we have

Note that σ<0 and that ψ(0,t)=ζ(0,t)=0.Thus,integrating (3.22) over (0,∞)×(0,t),choosing η suitably small,and using (3.23) and (3.24),we have
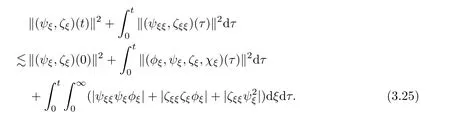

3.2 Proof of Theorem 1.3
In this subsection,we prove Theorem 1.3.Since it is easy to check the following local (in time) existence,we just state it and omit its proof for brevity:
Proposition 3.2
(local existence) Assume that the initial data (φ,ψ,ζ) satisfies that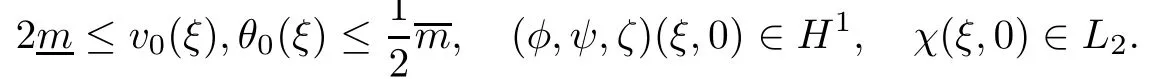
Then,the system (3.4) admits a unique solution (φ,ψ,ζ,χ) ∈X(0,t) for some sufficiently small t>0 satisfying that

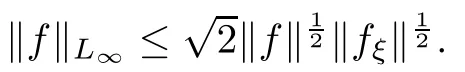
 Acta Mathematica Scientia(English Series)2021年1期
Acta Mathematica Scientia(English Series)2021年1期
- Acta Mathematica Scientia(English Series)的其它文章
- ON THE MIXED RADIAL-ANGULAR INTEGRABILITY OF MARCINKIEWICZ INTEGRALS WITH ROUGH KERNELS?
- THE LOCAL WELL-POSEDNESS OF A CHEMOTAXIS-SHALLOW WATER SYSTEM WITH VACUUM?
- UNDERSTANDING SCHUBERT’S BOOK(I)?
- GLEASON’S PROBLEM ON FOCK-SOBOLEV SPACES?
- ON THE CAUCHY PROBLEM FOR AW-RASCLE SYSTEM WITH LINEAR DAMPING?
- DOOB’S MAXIMAL INEQUALITIES FOR MARTINGALES IN VARIABLE LEBESGUE SPACE?
