DOOB’S MAXIMAL INEQUALITIES FOR MARTINGALES IN VARIABLE LEBESGUE SPACE?

Peide LIU(劉培德)

School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China E-mail:pdliu@whu.edu.cn

Abstract In this paper we deal with the martingales in variable Lebesgue space over a probability space.We first prove several basic inequalities for conditional expectation operators and give several norm convergence conditions for martingales in variable Lebesgue space.The main aim of this paper is to investigate the boundedness of weak-type and strong-type Doob’s maximal operators in martingale Lebesgue space with a variable exponent.In particular,we present two kinds of weak-type Doob’s maximal inequalities and some necessary and sufficient conditions for strong-type Doob’s maximal inequalities.Finally,we provide two counterexamples to show that the strong-type inequality does not hold in general variable Lebesgue spaces with p>1.

Key words variable Lebesgue space;martingale inequality;norm convergence;Doob’s maximal inequality

1 Introduction

In recent years,with development of the theory of the variable exponent Lebesgue spaces of functions,the variable exponent Lebesgue spaces of martingales have attracted more attention as well.Many facts show that the situation for martingales in variable exponent spaces is different from not only classical martingale spaces but also variable function spaces on R.A lot of efficient methods for the classical case can’t be used in the variable exponent case,so many results in classical martingale theory must be reconsidered.

The boundedness of the Hardy-Littlewood maximal operator is a central problem and plays a role in classical harmonic analysis.Diening[7]and Cruz-Uribe et al.[5]obtained its analogues in variable exponent function spaces under the conditions that the exponent p satisfies the so called log-H?lder continuity and a decay restriction at∞.Ever since,harmonic analysis with a variable exponent has developed rapidly,and many authors have studied its applications in a range of subjects.

Analogously,Doob’s maximal inequality is a major tool in classical martingale theory.Many authors have hoped to extend it to variable exponent martingale spaces.For example,in 2009,Aoyama [1]proved a weak-type inequality

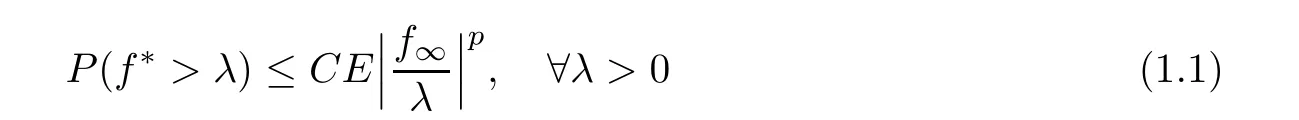
for every uniformly integrable martingale f=(f),when p satisfies

for every stopping time τ,where C is a constant depending only on p.In 2013,using a multiplier method,Nakai and Sadasue [17]proved that a strong-type Doob’s maximal operator is bounded in weighted variable Lebesgue space if every σ-algebra Σis generated by at most countable atoms.Recently,by using atom decomposition,Jiao et al.[11]studied several kinds of martingale inequalities in variable exponent spaces,including Doob’s maximal inequality.Specifically,under the conditions that every σ-algebra is generated by countable atoms and that p satisfies

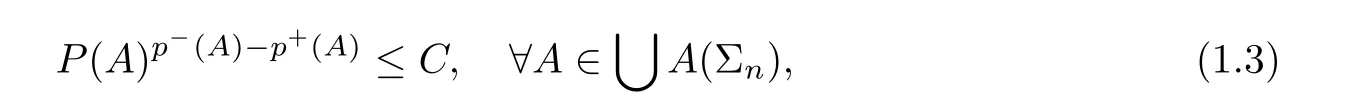
the weak-type and strong-type Doob’s maximal inequalities hold (for the definitions and notations,see [11]).However,up until now,the general form of strong-type Doob’s maximal inequality has been open.We also mention that in [14],the authors proved that the famous Burkholder-Gundy-Davis inequality and some other inequalities hold in variable exponent martingale Hardy spaces.

The main aim of this paper is to investigate the weak-type and strong-type Doob’s maximal inequalities in general forms for martingales in variable exponent spaces.In particular,for the Lebesgue space Lover a probability space(?,Σ,P)with variable exponent p,we prove that the weak-type maximal inequality

always holds without any additional restriction on p,and that its coefficient is sharp,when p is a constant,it would simply become a classical weak-type Doob’s maximal inequality.

We also prove another weak-type Doob’s maximal inequality

under the condition that the conditional expectation operators (E) are uniformly bounded in L,i.e.,

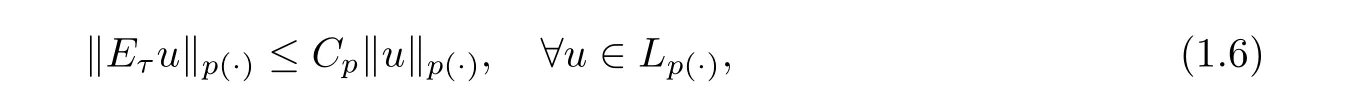
where τ is any stopping time with respect to (Σ).

After this,we prove that under the condition (1.6),the inequality

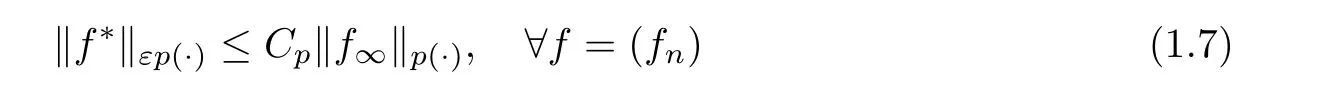
holds,where ε is a real with 0 <ε <1.Moreover,we also discuss some other properties of weak-type and strong-type Doob’s maximal operators.

This paper is arranged as follows:after the preliminaries,in Section 2,we give several pointwise inequalities for conditional expectation operators in variable Lebesque space,including the conditional H?lder’s inequality and the generalized conditional H?lder’s inequality.In Section 3 we establish several sufficient and necessary conditions for the norm convergence of martingales in variable Lebesque space.In Section 4 we prove two kinds of weak-type Doob’s maximal inequalities.In Section 5 we investigate the conditions for the strong-type Doob’s maximal inequality and some other properties of the strong-type Doob’s maximal operator.In the last section,we provide two counterexamples to show that in the case p>1,a.e.,strong-type Doob’s maximal inequality does not hold.

For detailed material about the variable Lebesgue spaces of functions and the Hardy-Littlewood maximal operator,we refer to [4]and [8].

2 Preliminaries

Let (?,Σ,μ) be a complete probability space,L(?) the set of all measurable functions(r.v.) on (?,Σ,μ),and E the expectation with respect to Σ.We say that p ∈P if p ∈L(?)with 1 ≤p(ω) ≤∞.For p ∈P,denote ?={ω ∈? :p(ω)=∞},and define the modular of u ∈L(?) as

and the variable Lebesgue space on (?,Σ,μ) as

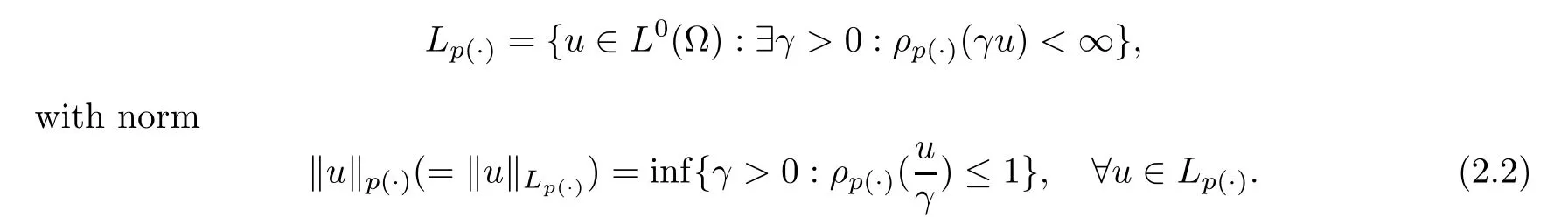
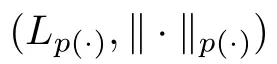
For u ∈L(?),we also define the quasi-norm as

if the last number is finite.The set of all such r.v.is called weak-Lspace,and we denote it by wL.A standard check shows that it is a quasi-Banach space,and by Kolmogolov’s inequality,

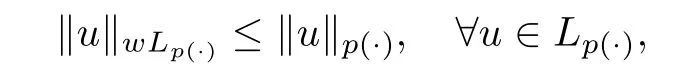
hence L?wL.

For p ∈P,we denote by pand pthe below index and the upper index of p:

Here we mention some basic facts about L(those are similar to the variable Lebesgue space of functions on R;see [9]or [13]).

Lemma 2.1

(see [9]) Let p ∈P with p<∞.Then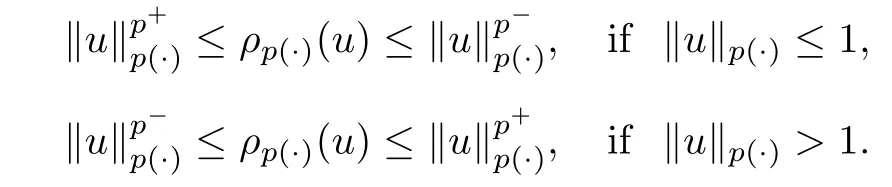

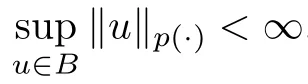
Lemma 2.2

(see [9]) Let p ∈P with p<∞and u,u ∈L.Then the following statements are equivalent: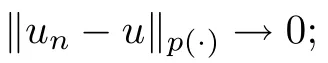

(2) ρ(u?u)→0;

(3) u→u in measure and ρ(u)→ρ(u).

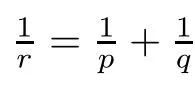
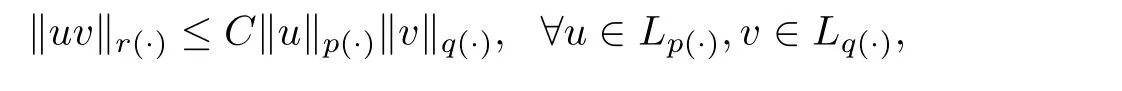
where C is a constant depending only on p,q and C ≤4 if r=1;C ≤2 if r=1,μ(p=∞)=μ(p=1)=0.

Lemma 2.4

(see [9,13]) Let p,q ∈P.Then L?Liff q(ω) ≤p(ω),a.e..In this case,

Lemma 2.5

(see [13]) Let p ∈P and u ∈L.Then

Lemma 2.6

(see [4,8]) Let p ∈P and sp≥1.Then

Here the first equation is well known.Indeed,

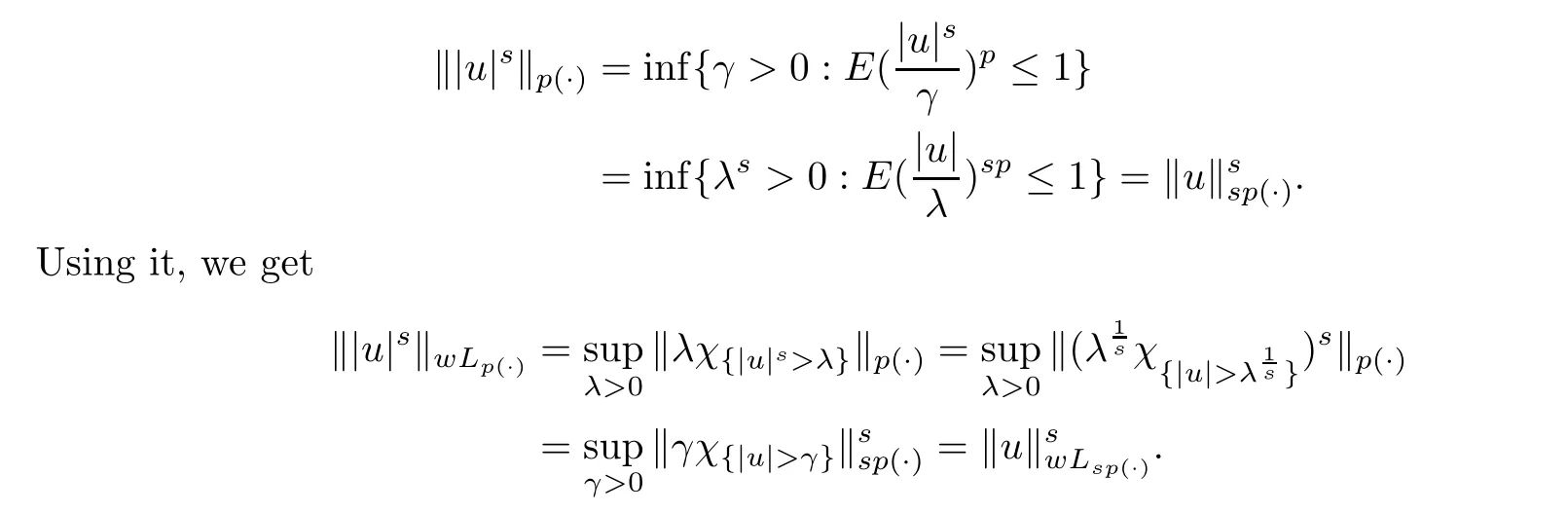
Let (Σ)be a nondecreasing sequence of sub-σ-algebras of Σ with Σ=σ(∪Σ),Ethe conditional expectation with respect to Σ,and f=(f)a martingale adapted to(Σ).As usual,we denote f’s pointwise limit and Doob’s maximal function as follows:

In this paper,we always denote by C some positive constant that is independent of the main parameters involved but whose value may be different in each appearance;and denote by Cor Csome positive constant depending only on p or p and ε,respectively.In what follows,we say that two quantities A and B are equivalent if there exists C >0 such that CA ≤B ≤CA.

3 Some Inequalities for Conditional Expectation

Let B be a sub-σ-algebra of Σ,u a r.v..We denote by E(u|B) the conditional expectation of u with respect to B.

Theorem 3.1

Let p,q,r ∈P.

(1) If u ∈L,v ∈Land u is B-measurable,then

(2) (Conditional H?lder inequality) If p is B-measurable,then

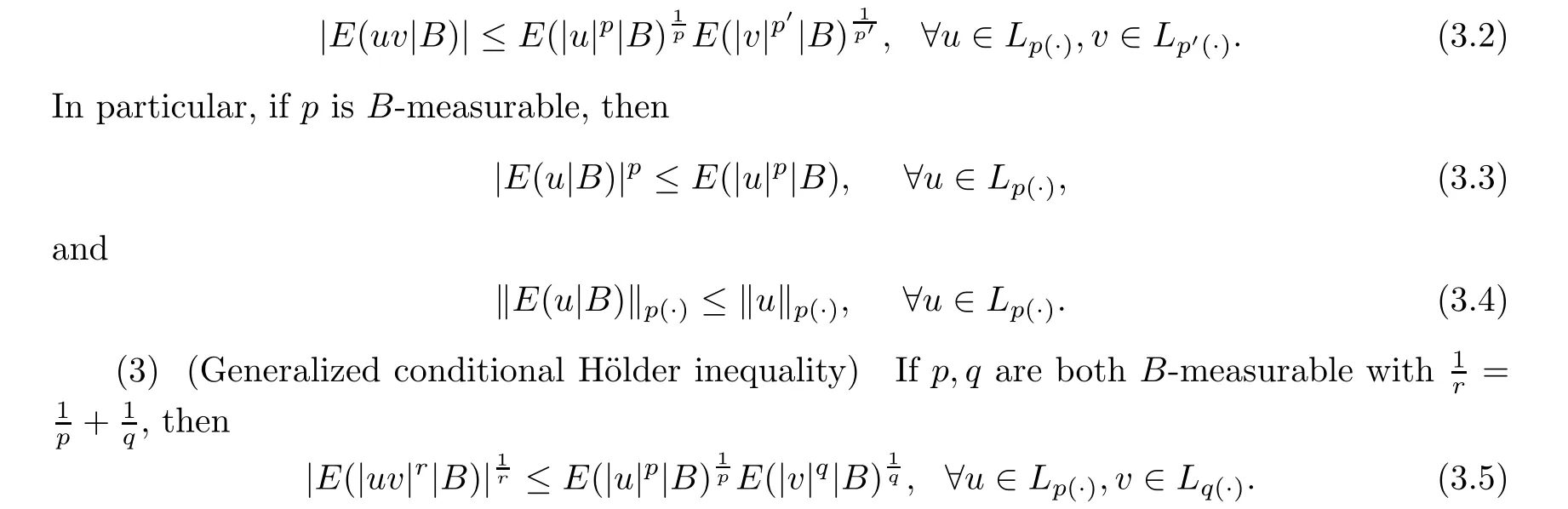
Proof

To prove (3.1),by Lemmas 2.4 and 2.3 we have u,v ∈Land uv ∈L;the left proof is similar to classical case.

To prove (3.2),by Young’s inequality we have

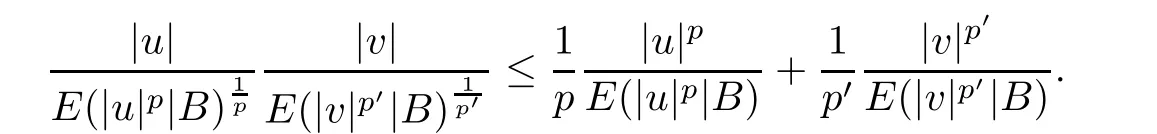
Take the conditional expectation with respect to B in both sides.Since p and pare Bmeasurable,we get

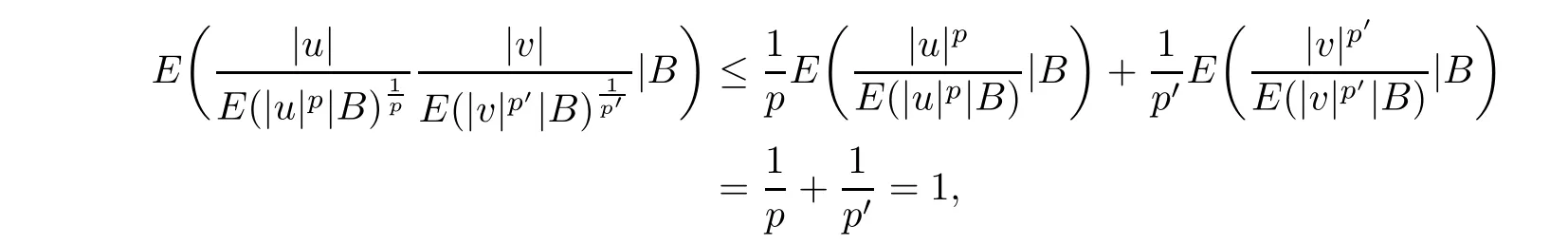
and by the measurable property,we get (3.2).Taking v ≡1 in (3.2),we obtain (3.3).Since E(·|B) is linear,from (3.3) and its definition,we obtain

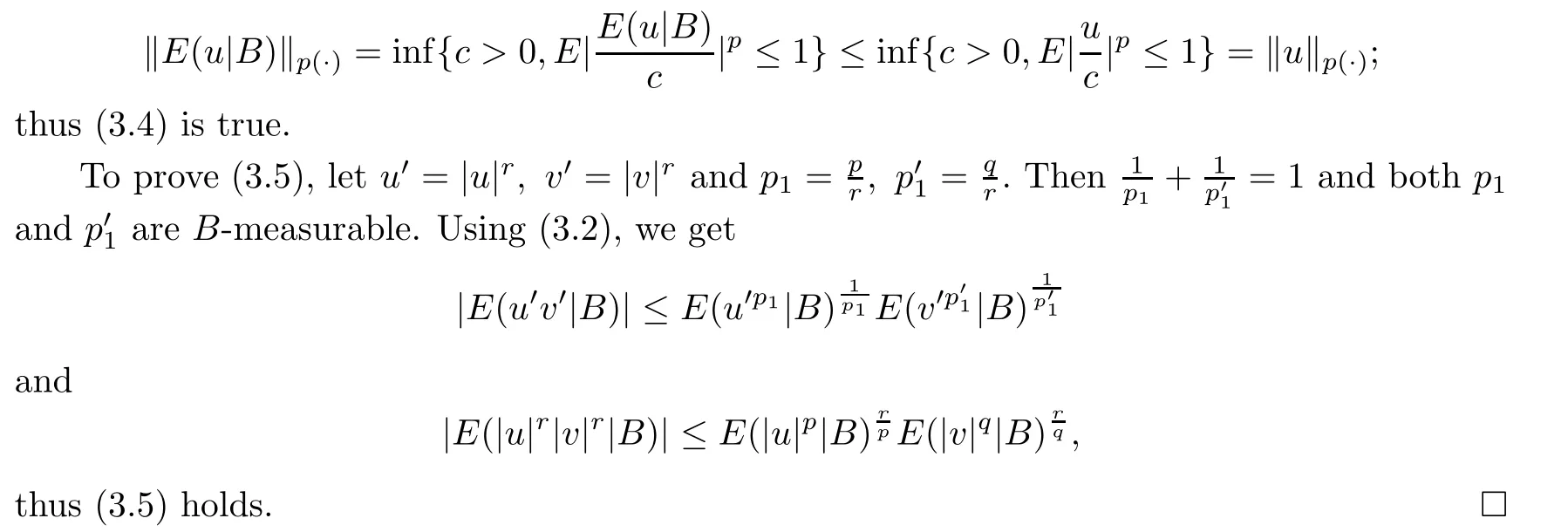
The inequality (3.4) shows that as an operator,E(·|B) is contractive on Lwhen p is measurable with respect to B.For another proof of this,see [1]lemma 1.This is not true in general case,however.

4 Norm Convergence Theorem

Recall that a family B of r.v.is said to be uniformly integrable if

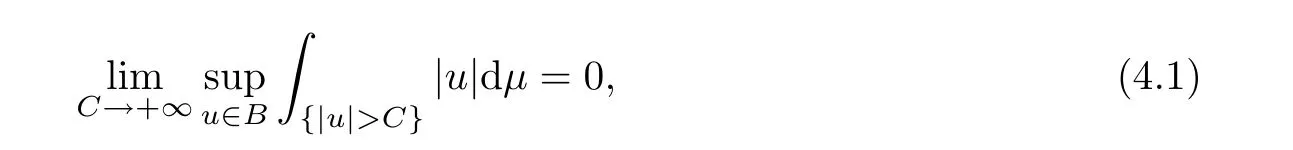
and that B is uniformly integrable iff B is Lbounded and their integrals have equi-absolutecontinuity.

Lemma 4.1

Let p ∈P with p<∞and let f=(f) be a martingale.

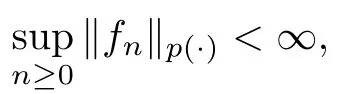
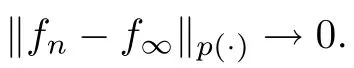
Proof

(1) Since p ≥1,from Lemma 2.4 we have that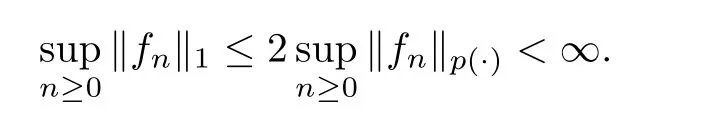

By Doob’s convergence theorem for martingales,f→fa.e.,and then |f|→|f|a.e..By Fatou’s lemma,ρ(f)≤sup ρ(f)<∞,so f∈L.

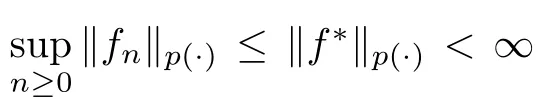
Now we investigate the norm convergence theorem of a martingale in L.

Theorem 4.2

Let p ∈P with p<∞and let f=(f)be a martingale.Then the following statements are equivalent:

(1) {|f|,n ≥0} is uniformly integrable;

(2) ρ(f)→ρ(f);

Proof

First of all,by Lemmas 2.1 and 4.1,every one of these four conditions implies that f→fa.e..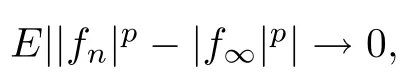

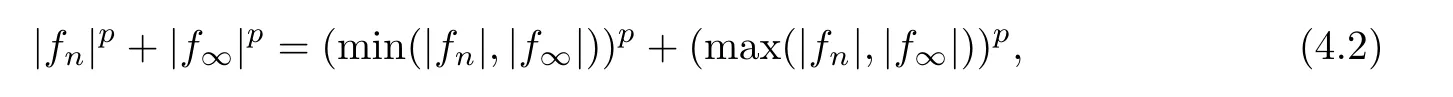
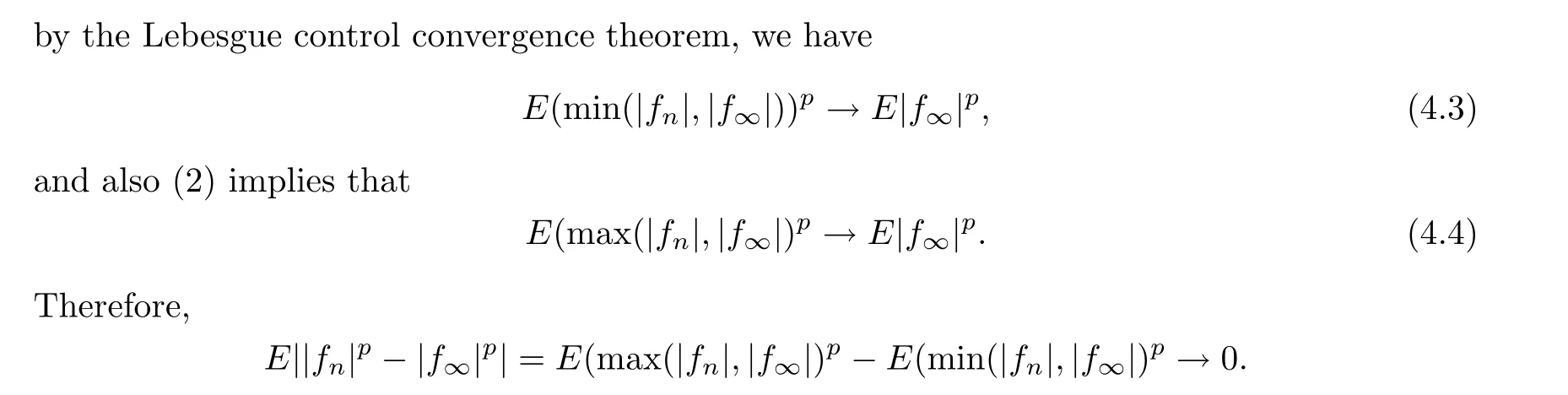
This implies the uniform integrability of {|f|,n ≥0},and thus (2)?(1) holds.

From Lemma 2.2,(2)?(4)is true.(4)?(3)is well known.To complete the proof,it is only needed to prove (3)?(4).

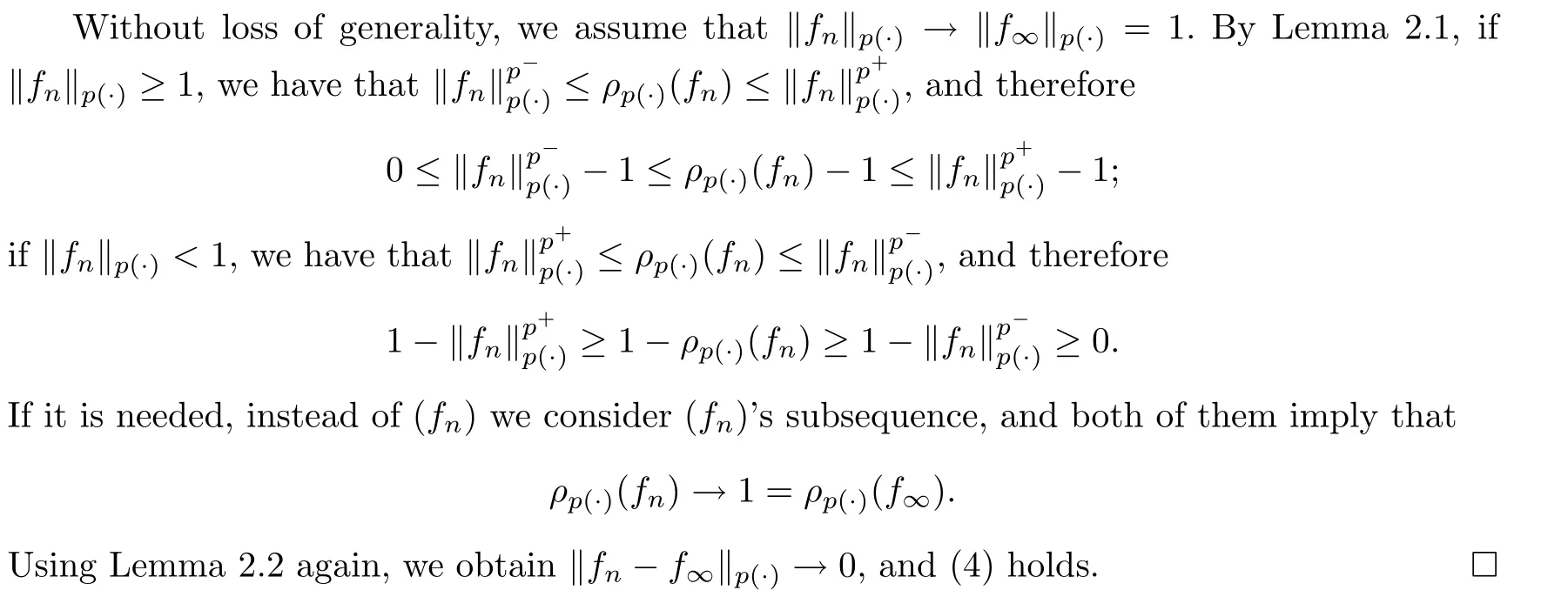
Another norm convergence theorem for a martingale in Lis Theorem 5.3 (1),below.

5 Weak-type Doob’s Maximal Inequalities

As analogues of the classical weak-type Doob’s maximal inequality,here we present two kinds of weak-type Doob’s maximal inequalities for a martingales in variable exponent space.

Proof

From the uniform integrability,we have f=E(f|Σ) (or f≤E(f|Σ) for a nonnegative submartingale)for all n ≥0,where fis its a.e.limit.We assume p>1.In the other case,p ≡1,inequality (5.1) is well known.

For λ>0,define

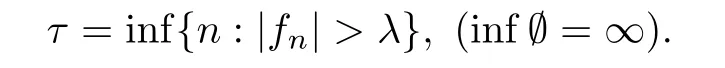
Then τ is a stopping time with {f>λ}={τ <∞} ?{|f| >λ}.Using Young’s inequality with a variable exponent,we get

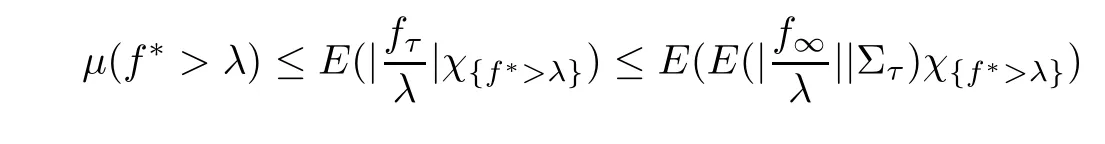
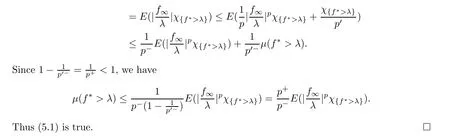
For another kind of weak-type Doob’s maximal inequality,we need the following definition:

Definition 5.2

Let p ∈P and (Σ)be a nondecreasing sequence of sub-σ-algebras of Σ.For every stopping time τ,denote conditional expectation operator E(u|Σ)=u=Eu,?u ∈L.We say that {E} is L-uniformly bounded if there is a C>0 such that

where τ is any stopping time with respect to (Σ).

It is easy to see that if Doob’s maximal operator is bounded in L,then {E} is L-uniformly bounded.

Theorem 5.3

Let p ∈P with p<∞,and let {E} be L-uniformly bounded.Then,

(1) For every f ∈L,f=E(f|Σ) converges in L.

(2) For any s>1,{E} is L-uniformly bounded.

(3) {E} is L-uniformly bounded iff it is L-uniformly bounded.

(2) If f ∈L,i.e.,|f|∈L,by Lemma 2.6 we get

(3) If {E} is L-uniformly bounded,from Lemma 2.5 we have

In what follows we shall use the concept of an averaging operator.Let A ∈Σ with|A|>0,where we denote by |A| the probability of A.We call the operator an averaging operator on A.

Theorem 5.4

Let p ∈P with p<∞.Then,for the following conditions,(1)?(2)?(3)?(4)hold:

(1) {E} is L-uniformly bounded.

(2) M is weakly bounded in L,and there is a C>0 such that

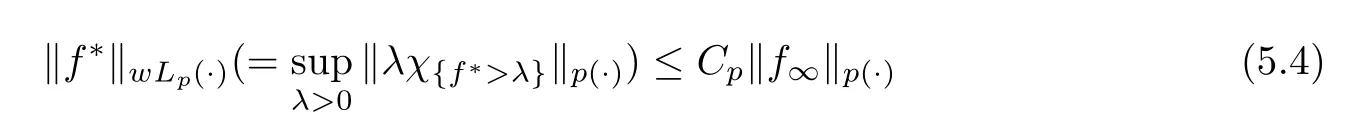
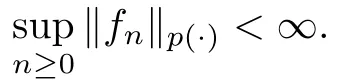
(3) Averaging operators Tare uniformly bounded on Lwith respect to A ∈Σ,and there is a C>0 such that

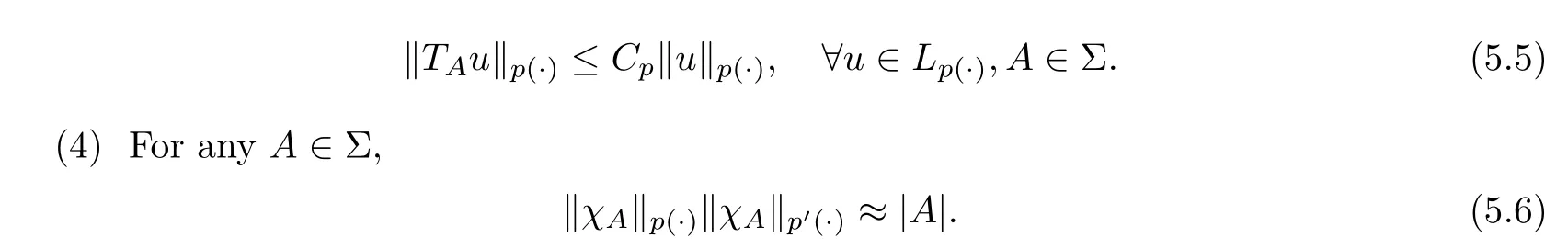
Proof

Proof of (1)?(2):for every λ >0,we define the stopping time τ as in the proof of Theorem 4.1,so we have {f>λ}?{|f|>λ}.Thus

This implies that (5.4) is true.

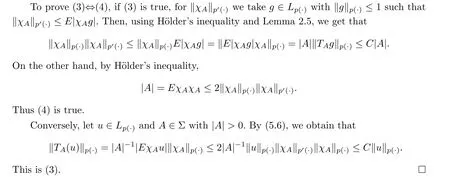
6 On Strong-type Doob’s Maximal Inequality

Recall that in classical harmonic analysis,the Hardy-Littlewood maximal operator is bounded in weighted Lspaces iff the weight w ∈A.In a weighted variable Lebesgue space of functions on R,an analogue was obtained by Cruz-Uribe and Diening.Here we consider the situation of martingales.First,by using Rubio de Francia’s iteration algorithm,we construct an Aweight from an Lmember.

Lemma 6.1

Let p ∈P.If Doob’s maximal operator M is bounded in Lmartingale space,given h ∈L,we define

Theorem 6.2

Let p ∈P with 1 (1) The operator M is L-bounded.

(2) For any s>1,M is L-bounded.

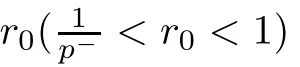
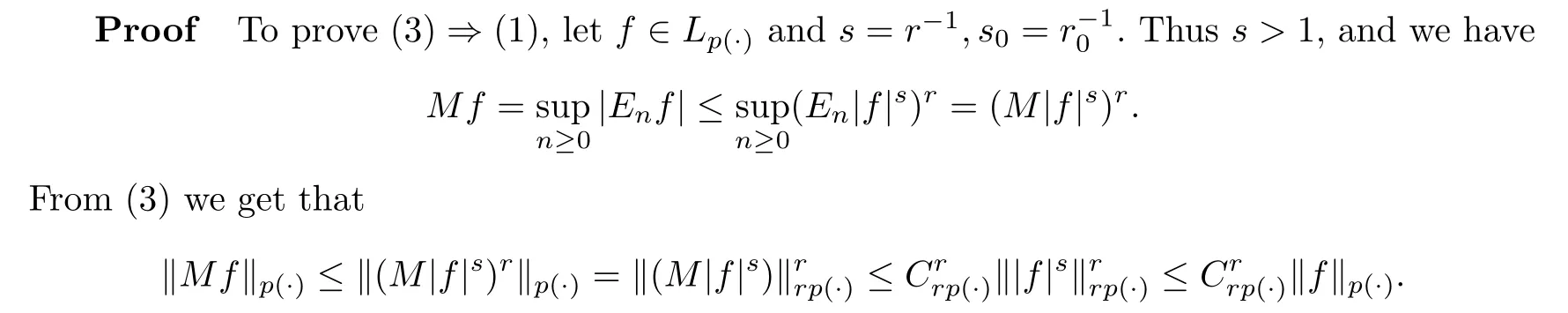
This is (1).The proof (1)?(2) is similar.

If (Σ)is regular,we prove (1)?(3) only,since the proof of (2)?(3) is similar.For h ∈L,we define ?h as (6.1).Since ?h ∈Aand (Σ)is regular,there exists s>1

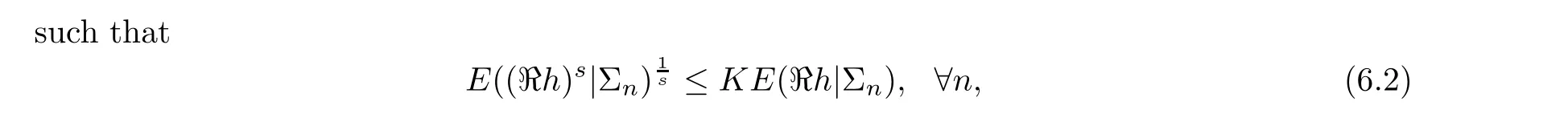
where 1

Theorem 6.3

Let p ∈P with 1

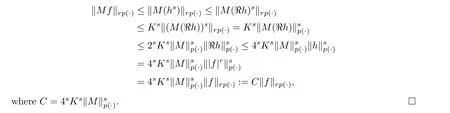
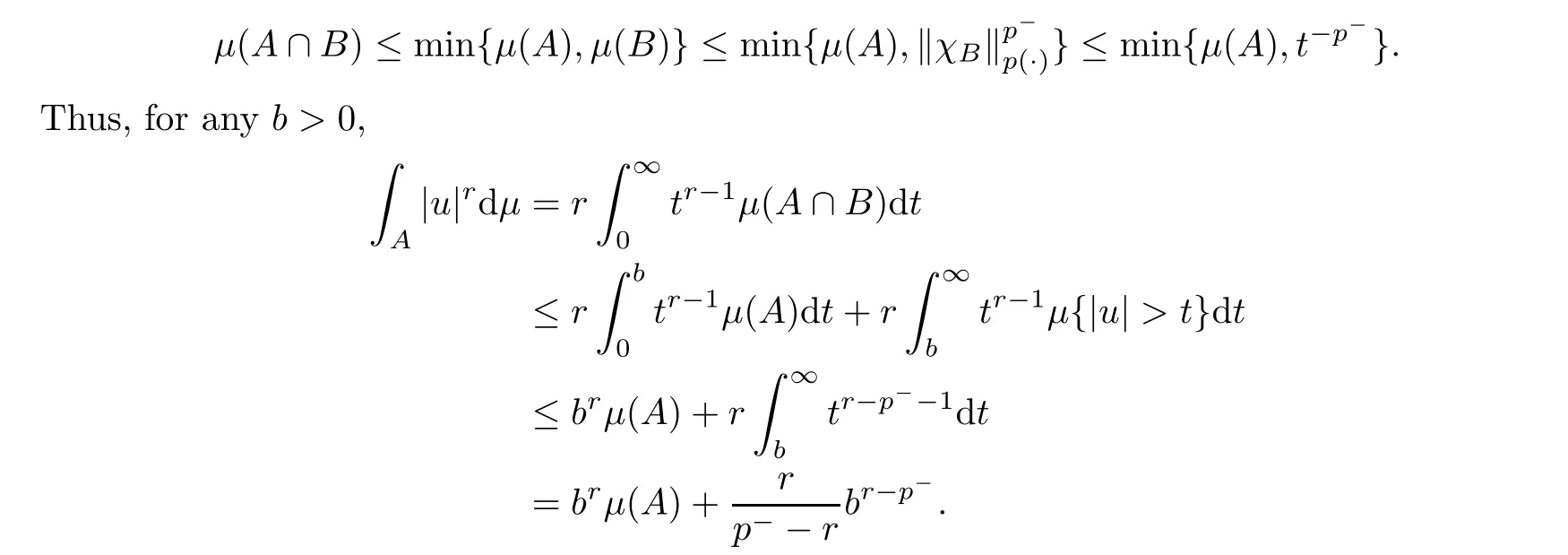
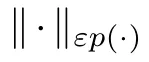
Remark 6.5

Unfortunately,the boundedness of a strong-type Doob’s maximal operator in Lis still unknown.Also,another problem is raised:what p can guarantee the L-uniform boundedness of {E}?

7 Two Examples

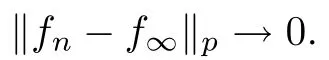
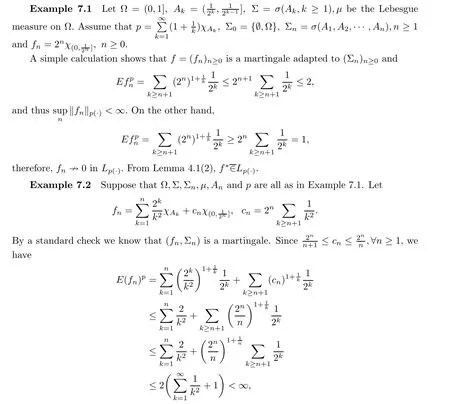
Acta Mathematica Scientia(English Series)2021年1期

Acta Mathematica Scientia(English Series)的其它文章

ON THE MIXED RADIAL-ANGULAR INTEGRABILITY OF MARCINKIEWICZ INTEGRALS WITH ROUGH KERNELS?

THE LOCAL WELL-POSEDNESS OF A CHEMOTAXIS-SHALLOW WATER SYSTEM WITH VACUUM?

UNDERSTANDING SCHUBERT’S BOOK(I)?

GLEASON’S PROBLEM ON FOCK-SOBOLEV SPACES?

THE EXISTENCE AND STABILITY OF STATIONARY SOLUTIONS OF THE INFLOW PROBLEM FOR FULL COMPRESSIBLE NAVIER-STOKES-POISSON SYSTEM?

ON THE CAUCHY PROBLEM FOR AW-RASCLE SYSTEM WITH LINEAR DAMPING?