GLEASON’S PROBLEM ON FOCK-SOBOLEV SPACES?
Jineng DAI(戴濟(jì)能)Jingyun ZHOU(周靜云)
Department of Mathematics,School of Science,Wuhan University of Technology,Wuhan 430070,China E-mail:jinengdai@whut.edu.cn;zhou19950614@163.com
Abstract In this article,we solve completely Gleason’s problem on Fock-Sobolev spaces Fp,mfor any non-negative integer m and 0 Key words Fock-Sobolev space;Gleason’s problem where dv is the normalized Lebesgue volume measure on Cso that the constant function 1 has norm 1 in L.Here we are abusing the term“norm”for 0 Let Fdenote the space of holomorphic functions in L.When m=0,the space Fis called the Fock space or the Segal-Bargmann space(see[1–7]).For a multi-index α=(α,···,α),where each α(1≤k≤n)is a non-negative integer,we write where?denotes partial differentiation with respect to the k-th component.An equivalent characterization for the space Fis as follows(see[4]):f∈Fif and only if?f belongs to the Fock space for each multi-index α with|α|≤m.In this sense we call Fthe Fock-Sobolev space.The space Fis a closed subspace of the Hilbert space Lwith inner product The orthogonal projection P :L→Fis given by where K(z,w) is the reproducing kernel of the Fock-Sobolev space F.It is well known that for all 0 In this article,we prefer to use the integral form of hto express the reproducing kernel of Fock-Sobolev spaces F. Let X be a space of holomorphic functions on a domain ? in C.Gleason’s problem for X is the following:if a ∈? and f ∈X,do there exist functions f,···,fin X such that In this article,we solve Gleason’s problem on Fock-Sobolev spaces Fin a stronger form for the full range of p with 0 for all z ∈C(see Theorem 2.9 and 2.10).Because the form of the Bergman kernel of F(especially for m ≥1) is a bit complicated,some techniques are used for dealing with many integrals. In this section,we begin with several useful lemmas,which are needed in the proof of the solvability of Gleason’s problem on Fock-Sobolev spaces F. Lemma 2.1 0.There exists a constant C only depending on p,α and β such that for all holomorphic functions f and anti-holomorphic functions g on C. Proof Lemma 2.2 Remark 2.5 An important tool for tackling the boundedness of integral operators on L(1 Lemma 2.6 Now we state our main results.We first solve Gleason’s problem on the Fock space,then we turn to generalized Fock-Sobolev spaces. Theorem 2.9 for all z in Cand f in F.1 Introduction

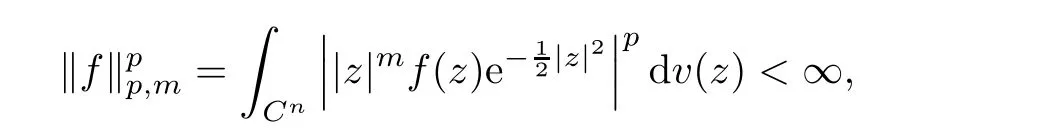
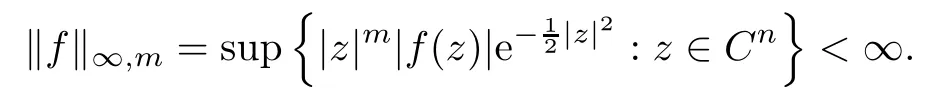
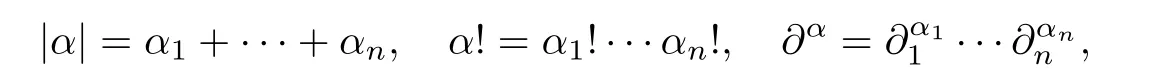



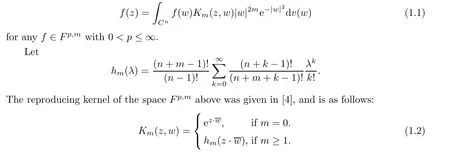




2 Gleason’s Problem on Fock-Sobolev Spaces
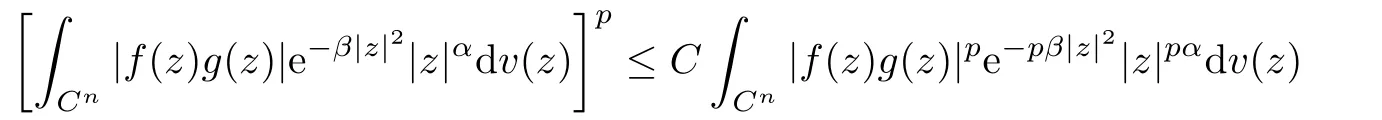
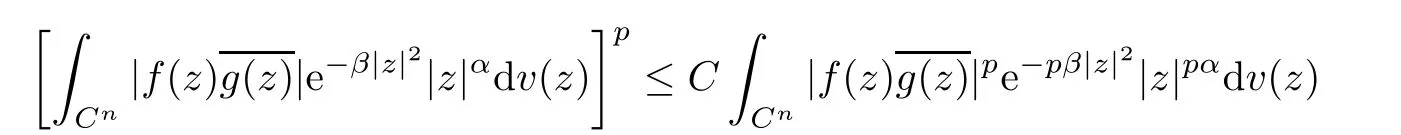

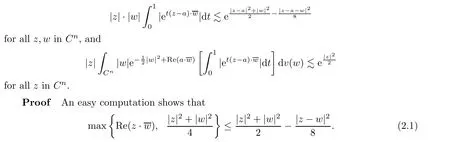


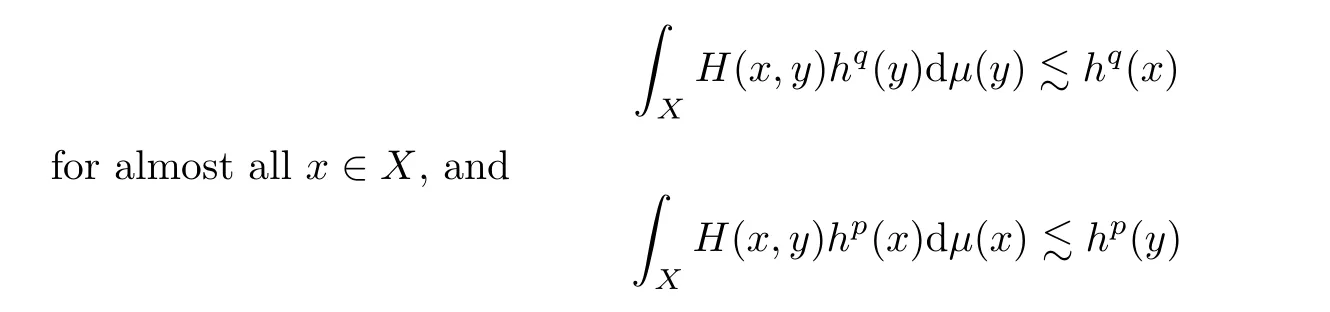



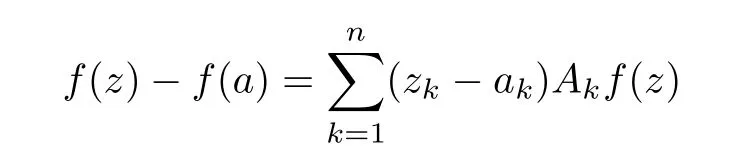



 Acta Mathematica Scientia(English Series)2021年1期
Acta Mathematica Scientia(English Series)2021年1期
