隧道開挖引起水平向位移被動樁的簡化計算方法

馮國輝　竇炳珺　張高鋒　丁士龍　徐長節

摘 要：目前，大部分盾構隧道開挖對鄰近樁基影響的理論研究是將被動樁簡化成單參數的Winkler地基模型和雙參數的Pasternak地基模型，較少考慮計算精度更高的三參數Kerr地基模型。基于Kerr地基模型建立被動樁的水平撓度控制方程，結合盾構隧道開挖施加的水平附加應力，利用差分法計算得到盾構開挖對鄰近樁基的數學矩陣解析表達式，進而得到被動樁的水平變形位移半解析解。兩個工程實例表明，Kerr地基模型比Winkler、Pasternak地基模型的計算結果與實測數據更接近。參數分析表明：隨著隧道直徑的增大，被動樁水平位移會增加;增大樁基的直徑，被動樁水平位移會減小;對于樁底以下隧道開挖情況，增大樁基與盾構開挖的水平距離和豎向凈距，被動樁水平位移均會減小。

關鍵詞：盾構開挖;地基模型;樁基變形;有限差分法

中圖分類號：TU473.1? ?文獻標志碼：A ??文章編號：2096-6717（2021）02-0010-09

Abstract： Currently， the theoretical studies on pile foundation deformation induced by adjacent tunneling are generally based on one parameter Winkler foundation model or two parameters Pasternak foundation model，rare studies have been considering in three parameters Kerr foundation model with greater computational accuracy. Based on Kerr foundation model， the governing equation of horizontal deflection of passive pile is established. Combining with the horizontal additional stress imposed by shield excavation， the analytical expression of the mathematical matrix of tunneling on the adjacent pile foundation is obtained using the difference method， and then the semi-analytical solution of the horizontal displacement of? the passive pile is obtained.Through? verification of two engineering cases， the Kerr foundation model is more consistent with the measured data than the Winkler and Pasternak foundation model.The results of parameter analysis show that the horizontal displacement increases with the increase of tunnel diameter. With increase of the passive pile diameter，horizontal displacement of the passive pile decreases.Passive pile displacement decreases with the increase of the horizontal distance or vertical distance between the passive pile and tunneling for the tunnel excavation under the pile bottom.

Keywords：tunneling;foundation model;pile displacement;finite difference method

盾構隧道開挖過程中會造成周邊地層的變形，這極有可能威脅到鄰近樁基的正常工作。準確預測盾構隧道開挖對鄰近樁基的影響已成為目前地下工程領域的一大研究熱點。

目前，已有很多學者對盾構隧道開挖引起鄰近樁基的影響進行了深入研究。分析方法主要分為3類：第1類室內試驗方法，Xiang等[1]利用透明土和PIV技術研究了隧道施工對周邊土體的影響，并得到土體位移的實測數據;周東等[2]利用透明土和PIV技術和光學測量系統設計了被動樁在側向位移作用下樁周土體測量的試驗方法，得到了樁基在不同埋置深度下樁周土體的位移場。第2類是利用大型商業有限元軟件來模擬盾構開挖對鄰近樁基的影響，有限元適用范圍廣，但使用較為復雜，需要準確地確定土層參數及邊界條件才能獲得較滿意的結果[3-4]。

第3類是理論解析法，理論解析是基于經典彈性力學，在考慮樁端邊界條件基礎上進行嚴格的理論推導。目前最主要的方法都是采用兩階段分析法：第1階段分析盾構隧道開挖引起樁基所在軸線處土體位移;第2階段將軸線處土體位移直接加到樁基上，再采用合理的模型模擬樁土相互作用，求解出樁基變形的解析解。理論分析法相比于實驗和有限元法物理意義明確，能夠精準地計算盾構隧道開挖引起的鄰近樁基變形。第1階段中， Loganathan等[5]提出了能夠準確預測盾構開挖引起地層位移的三維計算公式，因具其有良好的計算精度而被廣泛應用。李早等[6]、熊巨華等[7]基于Winkler地基梁模型并結合樁基兩端約束情況，采用有限差分法研究了盾構隧道開挖引起的鄰近樁基豎向位移及內力;梁發云等[8]基于Winkler地基模型，利用最小勢能原理建立被動樁變分控制方程，隨后解得被動樁位移及其內力;上官士青等[9]在研究鄰近堆載時，考慮到樁土水平位移不一致的情況，提出水平方向雙位移剛度矩陣，并通過多個算例驗證了其正確性。由于Winkler地基模型計算簡單，在工程領域得到廣泛的應用，但其表達式中忽略了土體的剪切變形，使得計算值與實際結果存在較大的誤差，為了克服這一缺點，Pasternak等[10]提出了具有考慮土體剪切變形的Pasternak地基模型，由于Pasternak地基模型的精確度較高而被廣泛地應用于地下工程研究中[11-12]。梁發云等[13]基于Pasternak地基模型分析得到水平受荷被動樁的位移和內力;Zhang等[14]將樁基簡化成Pasternak地基模型且考慮到樁土三維空間情況下盾構隧道開挖引起鄰近樁基的變形響應，驗證了考慮樁土三維空間作用能更精確地預測樁基變形。為了更加準確預測樁土相互作用的內力和變形，Kerr等[15]提出三參數Kerr地基模型，相比于Winkler地基模型和Pasternak地基模型，Kerr地基模型更具優越性，也有少數學者將其用于地下工程研究中[16-17]。

筆者在前人研究的基礎上，采用兩階段分析法，分析在盾構開挖作用下鄰近樁基的受力變形規律。基于Loganathan等（1998年）的修正后解析公式得到盾構開挖作用下樁基水平附加應力;采用Kerr三參數地基模型建立被動樁的水平位移控制微分方程，合理地提出了剪切層彎矩的假設，利用有限差分數值計算方法得到樁基水平位移控制方程的數學解析矩陣表達式，通過與實例分析對比驗證所提計算方法的有效性，并通過不同地基模型所得結果的比對說明三參數地基模型的優越性;最后，深入分析了隧道直徑、樁基直徑、樁隧中心線水平和豎向間距對樁基水平位移的影響。

1 Kerr地基模型下樁基簡化計算方法

1.1 單樁水平反應分析

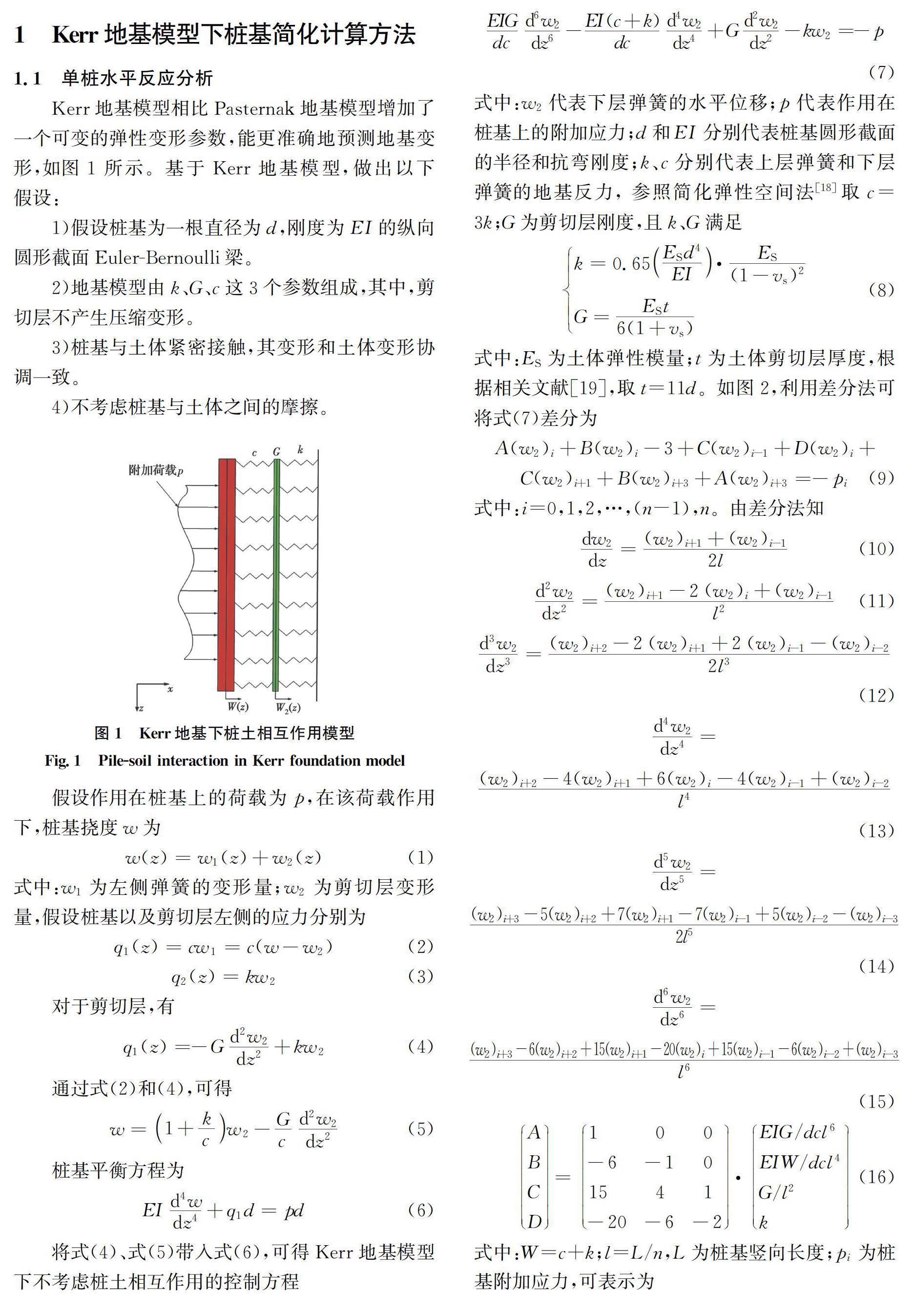
Kerr地基模型相比Pasternak地基模型增加了一個可變的彈性變形參數，能更準確地預測地基變形，如圖1所示。基于Kerr地基模型，做出以下假設：

1）假設樁基為一根直徑為d，剛度為EI的縱向圓形截面Euler-Bernoulli梁。

2）地基模型由k、G、c這3個參數組成，其中，剪切層不產生壓縮變形。

3）樁基與土體緊密接觸，其變形和土體變形協調一致。

4）不考慮樁基與土體之間的摩擦。

1.2 群樁水平位移分析

考慮到群樁中樁基對鄰近樁基的遮蔽效應使得樁基實際位移相對于其單樁時有所減少。在群樁基礎中，單個樁基的實際位移應該等于單樁位移和群樁遮蔽位移之和，其中，遮蔽位移與單樁自由位移方向相反。

參數選取原則同Kerr地基梁模型，具體計算見式（8）。3種不同地基模型計算所得的樁基撓曲變形曲線與實測數據對比見下節的算例分析。

2 算例分析

2.1 單樁實測驗證

以杭州在建地鐵側穿既有橋梁樁基工程為例，設計組根據實際情況，選擇隧道下穿鄰近既有樁基，具體設計如圖4所示。

取最靠近隧道中心線的樁1進行分析，樁長15 m，鉆孔灌注樁模量EP=30 GPa，樁截面為圓形，直徑1 m;隧道直徑7.7 m，隧道中心線距離地面H=20.18 m，隧道中心線到樁1最近水平距離x=4.96 m，豎向距離y=5.18 m，地層損失為ε0=1%，根據勘測數據可知，土體泊松比v=0.27。地層分布由上到下依次為雜填土、素填土、卵石、全風化粉砂巖、強風化粉砂巖、中風化粉砂巖，層狀分布，對于不同土層的土體模量采取加權平均法進行計算，得到土體模量ES=22 MPa。將橋梁樁基視為Euler-Bernoulli梁擱置在不同的地基模型上，分別得到不同地基模型下樁基的水平位移與實測數據的對比，如圖5所示。

由圖5可以看出，相比于Pasternak地基模型和Winkler地基模型，本文模型更加接近于實測數據，這是由于Winkler地基由于沒有考慮剪切層的影響，其結果與Kerr地基的結果差別較大。Pasternak模型較Winkler模型更為接近Kerr模型，但結果差別仍較大，說明第3個參數c的加入使得Kerr模型的結果更加準確。

2.2 群樁實測驗證

以浙江省某鄰近高鐵基樁的城市地鐵盾構工程為例[20]，設計組在盾構隧道和高鐵基樁之間建立一道隔離樁來保護鄰近的高鐵基樁，根據本文方法假定高鐵基樁和和隔離樁樁兩端均自由，具體設計如圖6所示。

由于中間兩個基樁有互相遮蔽位移的影響，最左側樁基受到的附加應力最大，本算例取4個鄰近高鐵基樁中最左側的樁基進行研究，如圖7所示。根據文獻[20]可知其工程參數，見表1，其中，隔離樁與高鐵基樁均為圓形截面，高鐵樁樁長35 m，取高鐵樁有效樁長也為15 m（高鐵基樁離地面超過15 m時，其基樁水平位移較小，可不考慮）。

如圖8所示，由文獻[21]可知，當樁中心距小于3倍樁徑時，堆卸載導致的土體側向位移在被動樁附近產生的側壓力90%以上的份額均由被動樁承擔，由此可知，本文中的隔離樁可等效成地下連續墻[22]，等效公式為

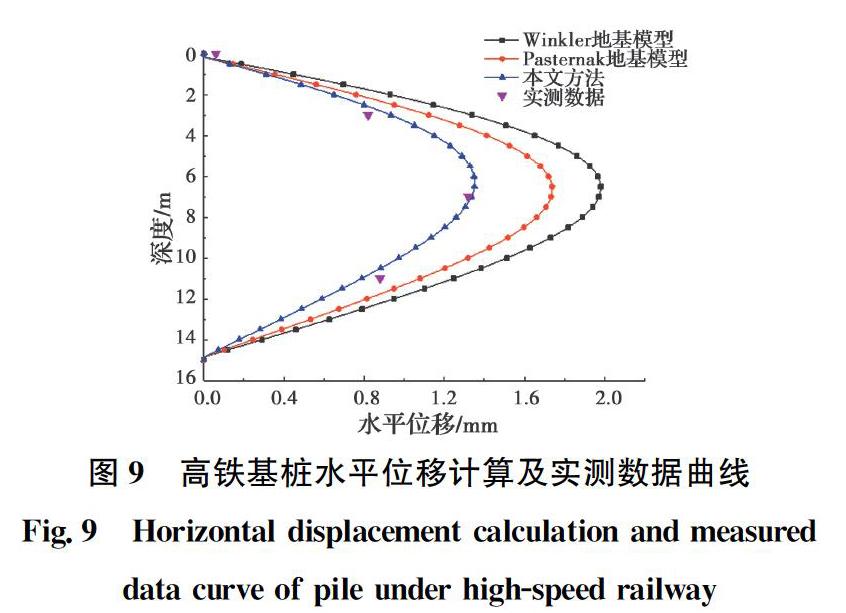
將隔離樁和高鐵基樁視為Euler-bernoulli梁擱置在不同的地基模型上，分別得到不同地基模型下高鐵基樁的水平位移與實測數據的對比，如圖9所示。

由圖9可以看出，相比于Pasternak地基模型和Winkler地基模型，本文模型更加接近于實測數據，3條曲線的發展趨勢一致，但Winkler地基模型僅考慮了土體之間的彈簧作用，計算得到的數據偏大，Pasternak在Winkler地基模型上考慮了土體的剪切作用，使得計算結果得到進一步優化，本文方法在Pasternak地基模型基礎上增加了可調節的彈簧系數c，使得計算結果更加精確，更加滿足實際工程數據。

3 參數分析

為了研究樁基直徑、隧道直徑、樁隧相對位置對樁基受力變形的影響，以杭州在建地鐵側穿既有橋梁樁基工程為例，其中x=y=5 m，其余參數不變。在研究某一參數對樁土相互作用的影響時，其余參數不變。

3.1 不同樁徑對樁基水平位移的影響

為了研究樁基受力變形與樁基直徑之間的關系，取5組不同的樁基直徑進行分析，分別為d=0.8、1.0、1.2、1.4、1.6 m，并采用本文方法計算樁基水平位移。

由圖10可以看出，隨著樁基深度的增加，樁身位移增加的趨勢沒有發生改變，但隨著樁基樁徑的增大，樁身水平位移增加的速率在逐漸減小，這是由于隨著樁徑的增大，樁基的剛度EI也逐漸增大，樁基的抗變形能力增強，造成樁身水平位移增速減小，故在工程實踐中，適度增大樁徑可以有效地控制開挖對鄰近樁基水平位移的影響。

3.2 不同隧道直徑對樁基水平位移的影響

為了研究樁基受力變形與隧道直徑之間的關系，取5組不同的隧道直徑進行分析，分別為R=0.8、1.0、1.2、1.4、1.6 m，并采用本文方法計算樁基水平位移。

由圖11可以看出，隨著隧道半徑的增大，樁基的水平位移也逐漸增大，且增大的速率也越來越明顯，這是由于隧道直徑的增大直接導致開挖隧道過程中地層應力產生較大改變，樁周土的附加應力快速變化，使得樁基水平位移增大且增速有加快的趨勢，故在工程實踐中要盡可能地減小隧道開挖直徑。

3.3 不同樁隧間距對樁基水平位移的影響

為了研究樁基受力變形與樁基和盾構開挖的水平距離和豎向凈距之間的關系，取多組不同的數據進行分析，令水平距離x=5 m不變，y/x=1、1.2、1.4、1.6、1.8，令y=5 m，x/y=1、1.2、1.4、1.6、1.8，采用本文方法計算這兩種情況下樁基水平位移并比較兩種不同情況對樁基水平位移的影響，如圖12所示。

由圖12可以看出，隨著x或者y的增大，樁基水平位移均會減小。這是由于隨著隧道中心線遠離樁基位置，隧道開挖在樁周產生的附加應力也會相應地減小，但對于樁底以下的隧道開挖過程，x、y增大相同的比例時，增大豎向距離y更能減小樁基的水平位移，這也符合實際工程中土體是成層分布的情況。一般來說，增大豎向位移會使隧道穿越更下層彈性模量更大的土層，隧道開挖產生的卸載應力在土體傳遞的過程中能夠充分消減，從而起到保護鄰近樁基的作用，此種工況下，應盡可能地增大隧道埋深以減小對鄰近樁基的影響。

4 結論

1）采用兩階段分析法，基于Loganathan求得隧道開挖卸荷作用下樁基水平附加應力;采用Kerr三參數地基模型建立被動樁的撓曲微分方程，提出了剪切層彎矩的假設，并利用有限差分數值計算方法推導出其數學解析矩陣表達式。

2）將本文結果與兩個工程實例及不同地基模型進行對比。分析結果表明，Winkler地基由于沒有考慮剪切層的影響，故其結果與Kerr模型結果差別較大。Pasternak模型較Winkler模型更為接近Kerr模型，但計算結果仍然沒有Kerr模型接近實測數據，兩個案例均說明Kerr地基模型相較其他模型更為準確。

3）在單樁分析過程中，增大樁基的直徑能減小樁基水平位移，但效果不明顯;增大隧道直徑會增大鄰近樁基的水平位移，且增大速率隨著隧道直徑增大有加速的趨勢。

4）對于隧道開挖在樁底以下的情況，相對于增大隧道中心線與樁基的水平距離，增大隧道的埋深更能減小鄰近樁基的水平位移。

參考文獻：

[1] XIANG Y Z， LIU H L， ZHANG W G， et al. Application of transparent soil model test and DEM simulation in study of tunnel failure mechanism [J].Tunnelling and Underground Space Technology， 2018， 74： 178-184.

[2] 周東， 劉漢龍， 仉文崗， 等. 被動樁側土體位移場的透明土模型試驗[J]. 巖土力學， 2019， 40（7）： 2686-2694.

ZHOU D， LIU H L， ZHANG W G， et al. Transparent soil model test on the displacement field of soil around single passive pile [J]. Rock and Soil Mechanics， 2019， 40（7）： 2686-2694.（in Chinese）

[3] LIU C， ZHANG Z X， REGUEIRO R A. Pile and pile group response to tunnelling using a large diameter slurry shield - Case study in Shanghai [J]. Computers and Geotechnics， 2014， 59： 21-43.

[4] SOOMRO M A， HONG Y， NG C W W， et al. Load transfer mechanism in pile group due to single tunnel advancement in stiff clay [J]. Tunnelling and Underground Space Technology， 2015， 45： 63-72.

[5] LOGANATHAN N， POULOS H G. Analytical prediction for tunneling-induced ground movements in clays [J]. Journal of Geotechnical and Geoenvironmental Engineering， 1998， 124（9）： 846-856.

[6] 李早， 黃茂松. 隧道開挖對群樁豎向位移和內力影響分析[J]. 巖土工程學報， 2007， 29（3）： 398-402.

LI Z， HUANG M S. Analysis of settlement and internal forces of group pile due to tunneling [J]. Chinese Journal of Geotechnical Engineering， 2007， 29（3）： 398-402.（in Chinese）

[7] 熊巨華， 王遠， 劉侃， 等. 隧道開挖對鄰近單樁豎向受力特性影響[J]. 巖土力學， 2013， 34（2）： 475-482.

XIONG J H， WANG Y， LIU K， et al. Effects of tunneling on vertical bearing behaviors of adjacent single pile [J]. Rock and Soil Mechanics， 2013， 34（2）： 475-482.（in Chinese）

[8] 梁發云， 張浩. 開挖土體側移作用下被動單樁能量變分分析方法[J]. 巖土工程學報， 2012， 34（Sup1）： 19-23.

LIANG F Y， ZHANG H. Variational solution of single passive pile subjected to lateral soil movement induced by adjacent excavation [J]. Chinese Journal of Geotechnical Engineering， 2012， 34（Sup1）： 19-23.（in Chinese）

[9] 上官士青， 楊敏， 李衛超. 分別考慮樁和土水平向位移的被動樁簡化算法[J]. 建筑結構學報， 2018， 39（1）： 162-172.

SHANGGUAN S Q， YANG M， LI W C. Simplified method of passive piles with independent lateral displacement of piles and soil [J]. Journal of Building Structures， 2018， 39（1）： 162-172.（in Chinese）

[10] PASTERNAK P L. On a new method of analysis of an elastic foundation by means of two-constants[M]. Moscow： Gosudarstvennoe Izdatelstvo Literaturi Po Stroitelstou i Arkhitekture，1954. （in Russian）

[11] 可文海， 管凌霄， 劉東海， 等. 盾構隧道下穿管道施工引起的管-土相互作用研究[J].巖土力學， 2020， 41（1）： 221-228， 234.

KE W H， GUAN L X， LIU D H， et al. Research on upper pipeline-soil interaction induced by shield tunneling [J]. Rock and Soil Mechanics， 2020， 41（1）： 221-228， 234. （in Chinese）

[12] 何小龍， 楊天鴻， 周云偉， 等. 考慮管–土分離的基坑開挖引起鄰近地下管線位移分析[J]. 土木與環境工程學報（中英文）， 2019， 41（6）， 9-16.

HE X L， YANG T H， ZHOUY W， et al. Analysis of pipeline displacement induced by adjoining foundation pit excavation considering pipeline-soil separation [J]. Journal of Civil and Environmental Engineering， 2019， 41（6）： 9-16. （in Chinese） ）

[13] 梁發云， 李彥初， 黃茂松. 基于Pasternak雙參數地基模型水平樁簡化分析方法[J]. 巖土工程學報， 2013， 35（Sup1）： 300-304.

LIANG F Y， LI Y C， HUANG M S， et al. Simplified method for laterally loaded piles based on Pasternak double-parameter spring model for foundations [J]. Chinese Journal of Geotechnical Engineering， 2013， 35（Sup1）： 300-304.（in Chinese）

[14] ZHANG Z G， HUANG M S， XU C， et al. Simplified solution for tunnel-soil-pile interaction in Pasternaks foundation model [J].Tunnelling and Underground Space Technology， 2018， 78： 146-158.

[15] KERR A D. A study of a new foundation model [J]. Acta Mechanica， 1965， 1（2）： 135-147.

[16] ZHANG D M， HUANG Z K， LI Z L， et al. Analytical solution for the response of an existing tunnel to a new tunnel excavation underneath [J]. Computers and Geotechnics， 2019， 108： 197-211.

[17] 王建軍， 陳福全， 李大勇. 低填方加筋路基沉降的Kerr模型解[J]. 巖土力學， 2019， 40（1）： 250-259.

WANG JJ， CHEN F Q， LI D Y. A simple solution of settlement for low reinforced embankments on Kerr foundation [J]. Rock and Soil Mechanics， 2019， 40（1）： 250-259.（in Chinese）

[18] 張治國， 姜蘊娟， 徐晨， 等. 對“考慮樁側土體三維效應和地基剪切變形的隧道開挖對鄰近樁基影響分析”討論的答復[J]. 巖土工程學報， 2018， 40（7）： 1360-1362.

ZHANG Z G，JIANG? Y J， XU C， et al. Reply to discussion on "Influence of tunneling on deflection of adjacent piles considering shearing deformation of foundation and 3D effects of lateral soils beside piles" [J]. Chinese Journal of Geotechnical Engineering， 2018， 40（7）： 1360-1362.（in Chinese）

[19] MORFIDIS K. Research and development of methods for the modeling of foundation structural elements and soil [D]. Thessaloniki： Aristotle University of Thessaloniki， 2003.

[20] 馮國輝， 周遜泉， 何慶亮， 等. 隔離樁對盾構掘進引起鄰近高鐵樁基水平位移的影響分析考[J]. 土木與環境工程學報（中英文）， 2020，42（4）： 28-35.

FENG G H， ZHOU X Q， HE Q L， et al. Analysis on the influence of isolation pile on horizontal displacement of adjacent pile under high-speed railway caused by shield driving[J]. Journal of Civil and Environmental Engineering， 2020，42（4）： 28-35. （in Chinese）

[21] 張建勛， 陳福全， 簡洪鈺. 被動樁中土拱效應問題的數值分析[J]. 巖土力學， 2004， 25（2）： 174-178， 184.

ZHANG J X， CHEN F Q， JIAN H Y. Numerical analysis of soil arching effects in passive piles [J]. Rock and Soil Mechanics， 2004， 25（2）： 174-178， 184.（in Chinese）

[22] VESIC A B. Bending of beams resting on isotropic elastic solid [J]. Journal of Engineering Mechanics， 1961， 87（2）： 35-54.

（編輯 王秀玲）