基于均勻設計及BP神經網絡的大體積混凝土熱學參數反分析

張玉平　馬超　李傳習　高樹威

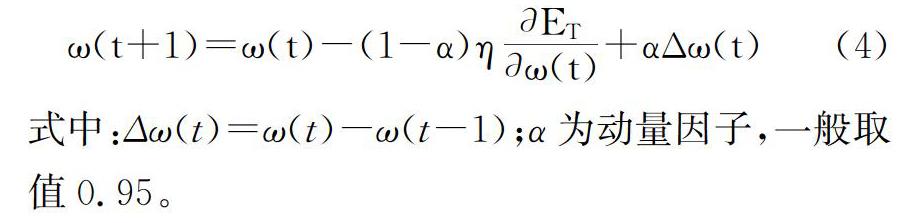
摘 要：為了解決橋梁工程大體積混凝土熱學參數失真的問題，提出一種基于均勻設計理論與BP神經網絡的大體積混凝土熱學參數反分析方法。該方法通過BP神經網絡建立大體積混凝土溫度場與熱學參數的非線性關系;BP神經網絡的訓練樣本由均勻設計方法確定;在BP神經網絡訓練階段，采用附加動量法對網絡結構進行優化;對優化前后的誤差曲線及多次訓練過程的分析結果表明：附加動量法可明顯縮短網絡訓練時間，多次訓練過程的平均絕對百分比誤差值及均方根誤差值穩定。在太洪長江大橋散索鞍支墩承臺大體積混凝土施工中反演了絕熱溫升、反應速率常數及導熱系數，基于反演值的溫度計算值與現場實測值吻合較好，溫度峰值最大誤差僅為1.1 ℃。基于均勻設計理論與BP神經網絡的大體積混凝土熱學參數反分析方法可行，且反演過程穩定收斂，反演精度高，應用于指導溫控施工能降低大體積混凝土開裂風險。

關鍵詞：橋梁工程;大體積混凝土;BP神經網絡;均勻設計;熱學參數;反分析

中圖分類號：U444;U445.57? ?文獻標志碼：A ??文章編號：2096-6717（2021）02-0148-10

Abstract： In order to solve the problem of distortion of thermal parameters of mass concrete in bridge engineering， an inverse analysis method of thermal parameters of mass concrete based on uniform design theory and BP neural network was proposed. This method uses BP neural network to establish the non-linear relationship between the temperature field and thermal parameters of large-volume concrete; training samples of BP neural network are determined by uniform design method; during the training phase of BP neural network， additional momentum method is used to optimize the network structure; The error curve before and after optimization and the analysis results of multiple training processes show that the additional momentum method can significantly shorten the network training time， and the average absolute percentage error value and root mean square error value of the multiple training processes are stable. The adiabatic temperature rise， reaction rate constant， and thermal conductivity were inverted during the construction of the bulk concrete of the supporting platform of the saddle pier of the Taihong Yangtze River Bridge. The calculated temperature based on the inversion value agrees well with the actual measured value， and the maximum temperature peak error is only 1.1 ℃. Therefore， the inverse analysis method for thermal parameters of large-volume concrete based on uniform design theory and BP neural network is feasible and the inversion process is stable and convergent， and the inversion accuracy is high. It can be used to guide the temperature-controlled construction to reduce the risk of large-scale concrete cracking.

Keywords：bridge engineering;mass concrete;BP neural network;uniform design;thermal parameters;inverse analysis

大體積混凝土作為現代橋梁的重要組成部分，其開裂問題一直是工程技術人員最為關注的問題之一。為了指導大體積混凝土施工，最大限度降低施工階段大體積混凝土的開裂風險，可根據現場實際施工狀況和現有的溫度場理論對其進行有限元分析。但是，在對大體積混凝土溫度場和應力場進行有限元分析時，所采用的熱學參數主要通過經驗公式或試驗得到，由于經驗公式難免有誤差，而試驗方法花費高、耗時長而較少使用，并且這些參數在施工期受氣象條件、時空、荷載、施工條件等多種因素影響，往往使得所采用的熱學參數失真，大體積溫控計算偏離甚至嚴重偏離實際情況，導致一些大體積混凝土結構出現或多或少的裂縫[1-2]，輕則影響結構的耐久性，重則產生工程質量事故，危及人民生命財產安全。因此，準確確定熱學參數是大體積混凝土溫控能否成功的基礎和前提，除試驗確定外，通過反演分析確定大體積混凝土的熱學參數也是行之有效的方法之一[3]。

目前，對大體積混凝土熱學參數的反演分析研究不多。王振紅等[4]基于施工現場的混凝土立方體非絕熱溫升試驗，對混凝土熱學參數進行了反分析。Amirfakhrian等[5]利用徑向基函數來獲得內熱源反分析的數值解。李守巨等[6]基于模糊理論建立了目標函數，將熱傳導反問題作為非線性優化問題處理。還有許多學者基于蟻群算法、粒子群算法、遺傳算法等優化算法提出熱學參數反演方法。但是，其中大部分研究還集中在壩體等水利工程中[7-9]，對橋梁工程中大體積混凝土熱學參數反分析較少[10-11]。喻正富等[10]基于施工現場測得的溫度數據，采用遺傳算法對大體積混凝土的熱力學參數進行了反演分析，但在反演過程中采取的是分步反演，而非同步反演。文豪等[11]對遺傳算法進行優化改進，提出在MATLAB中調用ANSYS溫度場數據，反演得到真實的熱學參數，但運用MATLAB調用數據，需另寫程序代碼，比較繁瑣。

為獲得混凝土真實的熱學參數，筆者將BP神經網絡引入到溫度場熱學參數反分析中，BP神經網絡特有的強大非線性映射能力可準確映射各熱學參數與溫度場之間的復雜非線性關系，結合實測數據即可快速、準確地反演混凝土熱學參數。此方法有效避免了采用經驗公式求解熱學參數時產生的誤差，還解決了因試驗設備昂貴或試驗過程漫長而未及時獲取熱學參數的問題。并且，在建立神經網絡的訓練樣本時引入均勻設計理論，可在一定程度上減少訓練樣本，提高效率。研究表明：基于均勻設計及BP神經網絡的反分析，得到了能反映大體積混凝土真實性能的多種熱學參數，使有限元仿真分析結果能準確地反映實際工程情況，及時采取的相應溫控措施避免了溫度裂縫的產生。

1 均勻設計與BP神經網絡的基本原理

1.1 均勻設計理論

均勻設計又稱均勻設計試驗法，是基于試驗點在整個試驗范圍內均勻散布的，從均勻性角度出發提出的一種試驗設計方法[12]，由方開泰教授和數學家王元在1978年共同提出。均勻設計表一般用符號Un（qs）表示，其中U表示均勻表，n表示試驗次數，q表示因素水平數，s表示最多可安排的因素數。其中，n=q，s=q-1，即均勻設計表的試驗次數n等于水平數q，最多可安排的因素數比水平數少1，而正交設計表中試驗次數n等于水平數q的平方，相比于正交設計試驗，均勻設計試驗可大大減少試驗次數。例如，某試驗有6個因素，每個因素取31個水平，其全部組合有316=887 503 681，若用正交設計至少需要312=961次試驗，而用均勻設計只需31次試驗，由此可見，均勻設計較正交設計更適用于多因素多水平試驗。

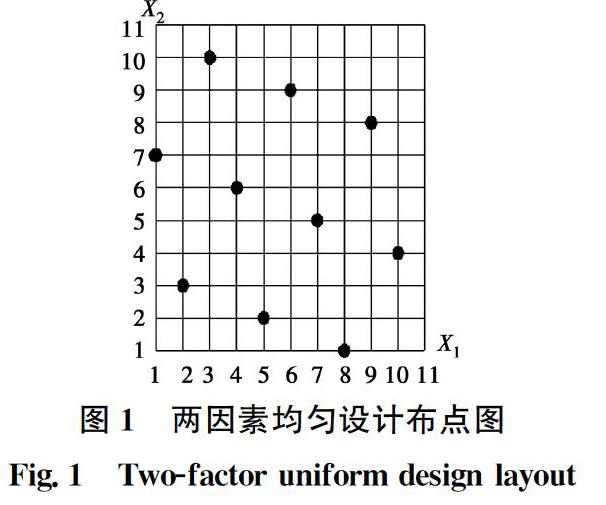
均勻試驗設計還具有一個鮮明的特點，即能從全面試驗點中挑選出部分代表性的試驗點，保證每個因素的每個水平做且僅做一次試驗。例如，做2因素11水平的試驗，應選用U11（1110）表，表中共有10列，最多可安排10個因素，現在有2個因素，根據U11（1110）的使用表，應取1、7列安排試驗，如圖1所示。當有4個因素時，應取1、2、5、7列安排試驗。筆者采用均勻設計理論確定熱學參數樣本，在保持樣本均勻性不變的前提下，可大幅提高計算效率。

1.2 BP神經網絡的基本原理

BP（Back Propagation）神經網絡[13]是目前應用最廣泛的一種前饋型神經網絡模型。在函數逼近、模式識別、分類問題、數據壓縮等領域均有廣泛應用。BP神經網絡由信息的正向傳播和誤差的反向傳播兩個過程組成。正向傳播中，輸入層接收外界信息并向隱含層傳播，隱含層負責信息變換，最終傳至輸出層。當實際輸出與期望輸出不符時，進入誤差的反向傳播階段。反向傳遞中，按誤差梯度下降的方式逐層反傳至隱含層、輸入層，直到預測輸出無限逼近期望輸出。BP神經網絡結構一般由輸入層、一個以上的隱含層、輸出層組成。理論證明，3層的BP神經網絡（單隱含層）可以實現從輸入到輸出的任意非線性映射。由圖2可見，若輸入層有m個神經元，輸出層有n個神經元，則可實現m維至n維的映射。

BP神經網絡最大的優點就是可以避免函數的具體形式，不必像顯式函數那樣需要提前確定定義域和值域，所以，在工程領域多應用于巖石力學中的巖石行為預測[14]、邊坡位移反分析[15]等問題中。混凝土熱學參數反分析同邊坡位移反分析一樣，均是復雜的非線性問題，難以用顯式的函數來描述，而這種復雜的非線性問題可以通過BP神經網絡得到較好的映射。

2 BP神經網絡反演分析方法

2.1 概述

反分析問題的求解方式一般分為解析反分析法和數值反分析法[16]。解析反分析法主要是通過找出現場監測值與待反演參數之間的顯式關系，建立數學模型，進而求得待反演參數。但是，由于實際工程問題的復雜多變性，一般難以確定其數學模型，顯式函數關系亦很難建立。因此，針對上述問題，有研究人員提出，建立反分析問題的目標函數，將參數求解問題轉化為目標函數最優解問題[17]，采用有限元法等數值方法進行迭代計算，并逐步修正待反參數，直至函數尋到最優解。但當反演參數比較多時操作起來將非常費時，因為尋優過程需要反復迭代，且對復雜問題搜索到最優解的概率較低。BP神經網絡為反分析問題提供了一條有效的途徑。其一，BP神經網絡由其特有的拓撲結構來表述反分析中的復雜非線性問題，無需建立數學模型;其二，BP神經網絡解決問題時，只需事先提供訓練樣本，完成訓練即可，無需反復迭代。

2.2 大體積混凝土溫度場影響因素分析

在溫度場分析中，主要熱學參數包括：混凝土的比熱c、密度ρ、導溫系數α、導熱系數λ、絕熱溫升θ0以及常數m。上述參數中混凝土的比熱c、密度ρ可直接測得，計算精度可滿足計算要求。絕熱溫升θ0受到水泥品種、用量、骨料粒徑以及實驗室環境與施工環境差異等多種因素的影響，如果不通過試驗確定就應進行反分析;導熱系數λ受混凝土密實性、材料特性以及骨料巖性的影響，難以確定，應予以反演。導熱系數λ=αcρ，因此，只需反演λ、α任意一個參數即可;水泥水化熱計算表達式主要有指數式、雙曲線式、復合指數式3種[1]。計算所用的水化熱表達式采用指數式函數θ（t）=θ0（1-e-mt），其常數m隨水泥品種、比表面及澆筑溫度不同而不同，更能體現施工現場實際澆筑環境，也確保所選表達式與有限元分析軟件熱源函數的定義保持一致。除絕熱溫升θ0外，還應對常數m進行反演。因此，選取絕熱溫升θ0、常數m、導熱系數λ作為反演參數，根據相關文獻，確定取值范圍見表1。

3 算例分析

3.1 工程概況

太洪長江大橋是主跨為808 m的鋼箱梁懸索橋，橋梁全長為1 436 m，為重慶南川至兩江新區高速公路NL5標段控制性工程。大橋南岸錨碇為隧道式錨碇，隧道錨混凝土施工包括后錨室、錨塞體、前錨室以及散索鞍支墩承臺，隧道錨立面布置見圖4。散索鞍支墩承臺分左右兩幅，每幅尺寸為15 m（長） ×13 m（寬）×6 m（高），混凝土澆筑總量約2 340 m3，是典型的大體積混凝土結構。支墩承臺分3層澆筑，每層澆筑厚度均為2 m，見圖5。采用C40混凝土，混凝土設計配合比的材料用量如表2所示。

3.2 溫度測點布置及監測方法

考慮到結構的對稱性和溫度的變化規律，選取1/4結構進行溫度測點布置，測點布置如圖6所示[18]。采用實時無線溫度綜合測試系統進行監測，可根據需要設置溫度采集頻率，溫度監測頻率為2 h采集一次。太洪長江大橋南岸散索鞍支墩承臺于2019年3月18日21：00開始澆筑，3月19日19：00澆筑完成，澆筑歷時22 h，測得混凝土入模溫度為16.9 ℃。為獲得真實的橋址環境，環境溫度從混凝土開盤前一星期開始監測，在施工現場的背陰處布置測點，把實測環境溫度輸入有限元模型，排除晝夜溫差干擾。溫度曲線如圖7所示。

3.3 有限元模型

采用通用有限元軟件 Midas FEA 建立有限元模型，共有87 035個單元，16 848個節點。如圖8所示。模型考慮基巖對混凝土水化熱的吸收作用，建立地基擴大模型，固定溫度取為20 ℃，基巖側面和底面給予固定約束。根據現場實際的施工過程，分為3個施工階段，即2 m一層。混凝土抗壓強度通過試驗確定，根據對試拌混凝土的各項技術指標檢測及抗壓強度試驗，得到7、28 d抗壓強度分別為44.2、49.7 MPa。

3.4 BP神經網絡的建立

3.4.1 隱含層的確定

神經網絡隱含層神經元個數的選擇對網絡的性能影響很大，所以，對層內神經元數目需要進行恰當的選擇。隱含層神經元的選擇十分復雜，目前并沒有統一的理論指導。隱含層神經元數目與待解決問題的特征、輸入與輸出單元數直接相關。通常情況下，隱含層神經元太少，網絡可能訓練不出來或網絡性能較差;若隱含層神經元太多，可能使訓練時間延長，訓練容易陷入局部極小值點，誤差也不一定達到最佳。一般情況下，僅能靠經驗和多次試驗來確定隱含層單元數。根據經驗，可以參照公式l=n+m+a進行設計。式中：l為隱含層神經元數目，n為輸入層單元數，m為輸出層節點數;a為1～10之間的調節常數。在經驗公式的基礎上，采用逐步增加隱含層單元數的變結構法，即開始放入比較少的隱含層單元數，學習一定次數后，性能不佳就增加隱含層單元數，一直達到比較理想的隱含層單元數為止。根據訓練數據，確定隱含層單元數為15，網絡允許最大誤差設為0.001，學習速率為0.05，進行網絡訓練。

3.4.2 樣本設計及數據歸一化處理

采用均勻設計方法確定參數樣本，參數的水平數取為31，選取均勻設計表為U31（3110），樣本值見表3。將表3的參數樣本數據輸入有限元計算模型，得到支墩承臺特征點的溫度計算值，見表4。

考慮到各參數之間的量綱影響以及小數值信息被大數值信息淹沒現象的發生，在處理輸入與輸出數據時，要用到歸一化方法。神經網絡模型采用tan-sigmod型傳遞函數，該函數的值域為[-1， 1]，因此，在計算過程中用式（1）預處理數據，通過實際樣本試算，使其全部歸一化到[-1， 1]區間內，歸一化公式為

歸一化用MATLAB語言實現。

[input_train，inputps]=mapminmax（P1）;

[output_train，outputps]=mapminmax（T1）;

其中：input_train和output_train為歸一化返回的值，結構體inputps和outputps是進行歸一化時所用的參數。

3.4.3 網絡訓練及效果評估

為了提高網絡訓練速度，使學習時間更短，同時保證訓練過程的穩定性，采用附加動量法對神經網絡進行優化，附加動量法是在每個加權調節量上加上一項正比例于前次加權變化量的值，使網絡在修正其權值時不僅考慮誤差在梯度上的作用，而且考慮在誤差曲面上變化趨勢的影響，在沒有附加動量的作用下，網絡可能陷入淺的局部極小值，利用附加動量可以帶動梯度下降過程，沖過狹窄的局部極小值，從而提高訓練速度。具體表達為

在網絡訓練前還需對一部分參數期望值先進行設置。網絡最大訓練次數設置為1 000次，訓練期望精度設置為1×10-4。網絡誤差梯度目標值設為默認值0，網絡訓練過程中，誤差梯度實際值約為0.004 76，與目標值0接近，認為誤差梯度符合要求。神經網絡訓練過程中，為了防止網絡的過度訓練而使泛化能力降低，設置有終止訓練功能的有效性檢查步數，即確認樣本的誤差曲線不再下降的連續迭代次數，在網絡訓練之前，對有效性檢查步數的值進行不同設定后分別進行試驗，最終確定為6。訓練過程誤差曲線見圖9，可以看出，優化后的訓練過程隨著訓練次數的遞增穩定收斂，比優化前更快、更早收斂。BP神經網絡訓練過程結果具有隨機性，為評估網絡訓練效果是否達到預期，用12組歸一化

后的數據多次反演來檢驗測試樣本訓練效果，以平均絕對百分比誤差（MAPE）和均方根誤差（RMSE）作為誤差評價指標。

式中：observes為預測值;predicted為設計值;亦稱真實值;N是樣本數。平均絕對百分比誤差又可稱為相對誤差的絕對值平均值，由于離差被絕對值化，不會出現正負相抵消的情況，因此，更能反映訓練效果的可信程度。與相對誤差類似，它是一個百分比值，即如果MAPE值為5，則表示預測值較真實值平均偏離5%。均方根誤差是用來衡量觀測值同真實值之間的偏差，RMSE值越小，表示精度越高。每次訓練的平均絕對百分比誤差、均方根誤差見表5，第

1次訓練的熱學參數設計值與預測值的趨勢見圖10，可以看出：平均絕對百分比誤差均小于10%，均方根誤差值均小于1.2，預測值與設計值擬合度較高，說明神經網絡模型對大體積混凝土預測精度較高，可以用來反演大體積混凝土熱學參數。

3.5 反演分析結果與檢驗

將特征點實測溫度值輸入網絡，輸出即為3個熱學參數的反演值，見表6。反分析完成后，還需對熱學參數反演值進行檢驗，具體方法是，將反演值輸入有限元模型，計算出第2個施工階段特征點處溫度計算值，并與該施工階段測得的實際溫度值進行比較，檢驗二者的擬合程度，計算溫度值與實測溫度值擬合曲線如圖11～圖14所示。由圖可知，溫度計算值與實測值之間的誤差較小，變化規律基本一致，表明基于BP神經網絡反演得到的熱學參數符合混凝土的實際施工環境，該組反演值真實可靠。

4 結論

以太洪長江大橋散索鞍支墩承臺為工程背景，為得到混凝土真實的熱學參數，基于均勻設計和 BP神經網絡對大體積混凝土絕熱溫升、反應速率、導熱系數等熱學參數進行反演，揭示了溫度場與熱學參數之間的內在聯系和規律，得到如下結論：

1）施工期大體積混凝土的溫度峰值與混凝土熱學參數之間的復雜非線性關系可由BP神經網絡表述完成，運用BP神經網絡可避免主觀調整熱學參數所造成的誤差，有較強的實用性。

2）在BP神經網絡訓練階段，采用附加動量法優化網絡結構能明顯減少網絡訓練時間，提高訓練效率。

3）利用均勻設計和BP神經網絡相結合的反分析方法，可以大大減少網絡學習的樣本數量。同時，可使有限元正分析與反分析過程分離，大大減少了反分析時間，提高了反分析效率和準確性。

4）通過BP神經網絡反分析得到的大體積混凝土熱學參數分別為：絕熱溫升θ0=46.834 2 ℃，常數m=0.979 504，導熱系數λ=9.742 07 kJ/（m·h·℃），結合有限元正分析對后續施工的混凝土溫度場進行預測，得到的特征點溫度計算值與溫度實測值較為接近，在變化規律上基本吻合，溫度峰值最大誤差僅為1.1 ℃，表明基于均勻設計及BP神經網絡方法可較準確地反演大體積混凝土熱學參數。

參考文獻：

[1] 朱伯芳. 大體積混凝土溫度應力與溫度控制[M]. 北京： 中國水利水電出版社， 2012： 738.

ZHU B F. Thermal stresses and temperature control of mass concrete [M]. Beijing： China Water Power Press， 2012： 738.

[2] HATTEL J H， THORBORG J. A numerical model for predicting the thermomechanical conditions during hydration of early-age concrete [J]. Applied Mathematical Modelling， 2003， 27（1）： 1-26.

[3] 朱岳明， 劉勇軍， 謝先坤. 確定混凝土溫度特性多參數的試驗與反演分析[J]. 巖土工程學報， 2002， 24（2）： 175-177.

ZHU Y M， LIU Y J， XIE X K. Determination of thermal parameters of concrete by reverse analysis of test results [J]. Chinese Journal of Geotechnical Engineering， 2002， 24（2）： 175-177. （in Chinese）

[4] 王振紅， 朱岳明， 武圈懷， 等. 混凝土熱學參數試驗與反分析研究[J]. 巖土力學， 2009， 30（6）： 1821-1825， 1830.

WANG Z H， ZHU Y M， WU Q H， et al. Thermal parameters of concrete by test and back analysis [J]. Rock and Soil Mechanics， 2009， 30（6）： 1821-1825， 1830. （in Chinese）

[5] AMIRFAKHRIAN M， ARGHAND M， KANSA E J. A new approximate method for an inverse time-dependent heat source problem using fundamental solutions and RBFs [J]. Engineering Analysis with Boundary Elements， 2016， 64： 278-289.

[6] 李守巨， 劉迎曦. 基于模糊理論的混凝土熱力學參數識別方法[J]. 巖土力學， 2004， 25（4）： 570-573.

LI S J， LIU Y X. Identification of concrete thermal parameters based on fuzzy theory [J]. Rock and Soil Mechanics， 2004， 25（4）： 570-573. （in Chinese）

[7] 孫偉， 何蘊龍. 基于改進遺傳算法的墊層區混凝土熱學參數反演和早期裂縫成因分析[J]. 武漢大學學報（工學版）， 2014， 47（2）： 193-200.

SUN W， HE Y L. Inversion analysis of thermal parameters of cushion concrete and reasons of early stage cracks based on improved genetic algorithms [J]. Engineering Journal of Wuhan University， 2014， 47（2）： 193-200. （in Chinese）

[8] 倪智強， 周蘭庭. 基于改進蟻群算法的混凝土壩熱學參數反演[J]. 水電能源科學， 2018， 36（4）： 82-85.

NI Z Q， ZHOU L T. Inverse analysis of concrete dam thermal parameters based on improved ant colonyalgorithm [J]. Water Resources and Power， 2018， 36（4）： 82-85. （in Chinese）

[9] 王峰， 周宜紅， 趙春菊， 等. 基于改進粒子群算法的混凝土壩熱學參數反演研究[J]. 振動與沖擊， 2019， 38（12）： 168-174， 181.

WANG F， ZHOU Y H， ZHAO C J， et al. Inverse analysis of concrete dam thermal parameters based on an improved particle swarm optimization method [J]. Journal of Vibration and Shock， 2019， 38（12）： 168-174， 181. （in Chinese）

[10] 喻正富， 張筱雨， 劉來君， 等. 基于遺傳算法的大體積混凝土熱力學參數反演分析[J]. 建筑科學與工程學報， 2015， 32（5）： 81-88.

YU Z F， ZHANG X Y， LIU L J， et al. Inverse analysis of mass concrete thermal parameter based on genetic algorithm [J]. Journal of Architecture and Civil Engineering， 2015， 32（5）： 81-88. （in Chinese）

[11] 文豪， 王高峰， 侯章偉. 基于MATLAB和ANSYS的大體積混凝土水化熱效應分析[J]. 內蒙古公路與運輸， 2018（3）： 5-10.

WEN H， WANG G F， HOU Z W. Hydration heat effect analysis of massive concrete based on MATLAB and ANSYS [J]. Highways & Transportation in Inner Mongolia， 2018（3）： 5-10. （in Chinese）

[12] 方開泰. 實用回歸分析[M]. 北京： 科學出版社， 1988.

FANG K T. Practical regression analysis [M]. Beijing： Science Press， 1988.（in Chinese）

[13] 周品. MATLAB神經網絡設計與應用[M]. 北京： 清華大學出版社， 2013.

ZHOU P. Design and application of MATLAB neural network [M]. Beijing： Tsinghua University Press， 2013.（in Chinese）

[14] 張清， 宋家蓉. 利用神經元網絡預測巖石或巖石工程的力學性態[J]. 巖石力學與工程學報， 1992， 11（1）： 35-43.

ZHANG Q， SONG J R. Predicting mechanical behaviors of rock or rock engineering by neural network [J]. Chinese Journal of Rock Mechanics and Engineering， 1992， 11（1）： 35-43. （in Chinese）

[15] 李端有， 李迪， 馬水山. 三峽永久船閘開挖邊坡巖體力學參數反分析[J]. 長江科學院院報， 1998， 15（2）： 10-13.

LI D Y， LI D， MA S S. Backward analysis of the rock mass mechanical parameters in excavated slope of TGP permanent lock [J]. Journal of Yangtze River Scientific Research Institute， 1998， 15（2）： 10-13. （in Chinese）

[16] 宮經偉. 水工準大體積混凝土分布式光纖溫度監測與智能反饋研究[D]. 武漢： 武漢大學， 2013.

GONG J W. Study on temperature monitoring by distributed optical fible and the intelligent feedback for hydraulic quasi-mass concrete structure [D]. Wuhan： Wuhan University， 2013.（in Chinese）

[17] CHEN G R， YANG B. Back analysis of thermal parameters of mass concrete and its application based on micro-genetic algorithm [J]. Advanced Materials Research， 2014， 936： 1463-1467.

[18] 張玉平， 李傳習， 張磊， 等. 張花高速澧水大橋索塔基礎大體積混凝土溫控[J]. 科技導報， 2012， 30（34）： 55-60.

ZHANG Y P， LI C X， ZHANG L， et al. Mass concrete temperature control of Lishui bridge tower foundation in Zhanghua highway [J]. Science & Technology Review， 2012， 30（34）： 55-60. （in Chinese）

（編輯 王秀玲）