改進的基于奇異值分解的抗差容積卡爾曼濾波算法在全球定位導航中的應用

王姚宇, 陳仁文*, 張 祥

(1.南京航空航天大學機械結構力學及控制國家重點實驗室, 南京 210016； 2.東南大學信息科學與工程學院, 南京 211102)

非線性動態系統的非線性和噪聲不確定問題,導致傳統卡爾曼濾波不適用于非線性模型的狀態估計[1-2]。擴展卡爾曼濾波(extended Kalman filter，EKF)雖然可用于非線性系統濾波[3-5],但是其線性化環節會引入高階截斷誤差,且Jacobi矩陣的計算會增加運算的難度,在實際工程應用中效果不佳。無跡卡爾曼濾波(unscented Kalman filter，UKF)克服了EKF的局限性[6-10],UKF基于(unscented transformation，UT)變換構建了一系列Sigma點,以此逼近狀態向量的后驗概率密度函數,實現簡單且精度遠遠高于EKF,但是在狀態發生突變的情況下,UKF的魯棒性不佳,精度容易受到影響。容積卡爾曼濾波(cubature Kalman filter，CKF)利用三階球面徑向容積準則對概率密度函數進行近似[11-14],其采樣點的權值均為正數,相較于上述濾波算法,CKF的精度和穩定性都有所提高,為解決非線性估計問題提供了一個新思路。

但是非線性濾波普遍存在跟蹤能力弱和自適應能力差的問題,當系統受到異常觀測值或者狀態突變的影響時,濾波器容易產生精度降低甚至發散的情況。文獻[15]提出了均值濾波的思想對采樣數據進行了預處理,降低了異常觀測值的干擾,增快了系統的響應時間。文獻[16-17]中引入了奇異值分解(singular value decomposition，SVD)的辦法,減小了先驗協方差矩陣負定性變化,保證算法可以平穩地迭代。文獻[18]提出一種抗差方法,能夠有效減弱波動較大數據對于濾波器穩定性的影響。

在卡爾曼濾波器進行迭代更新時,波動較大的數據采集點會減慢濾波器的收斂速度,影響數據的穩定性。在工程試驗中,環境干擾會引入較大的噪聲,對量測數據產生影響,嚴重偏離真實值。為了解決濾波更新狀態不穩定和異常觀測值影響大的問題,提出一種改進的基于SVD的CKF抗差算法,采用均值濾波的方法,對干擾大的數據、瞬時脈沖信號等進行處理,同時使用抗差方法減弱異常觀測值的影響,使濾波器可以更好地運行下去,改善濾波效果,提高濾波器更新迭代的穩定性,對異常觀測值有較好的修正效果。計算仿真驗證該算法的有效性。

1 算法描述

1.1 均值濾波

均值濾波的思想是先選取一個長度為N的均值濾波窗口,從頭開始,以N個采樣數據為一組,求取其均值作為一個新的采樣點,隨后將窗口向后移動一個數據,用新的采樣數據替換掉窗口的第1個采樣數據,以此類推,獲得一組求取均值后的新的采樣點,作為濾波器的輸入值[19],其基本工作原理如圖1所示。

圖1 均值濾波基本工作原理Fig.1 Basic working principle of mean filtering

均值濾波的原理用算式可以表示為

(1)

式(1)中：y(i)為原采樣數據；Y(n)為均值濾波后新產生的數據,對于長度為M的數據列而言,n=1,2, 3,…,M-N,N為均值濾波窗口長度。均值濾波窗口的長度可以根據實際采樣點數的多少進行調節,合適的窗口大小可以獲得更好的濾波效果。

1.2 SVD分解

隨著容積卡爾曼濾波器的不斷迭代,狀態向量和觀測向量的協方差陣可能會出現負定的情況,導致濾波器的狀態無法準確更新,甚至出現無法收斂的現象。SVD分解也叫奇異值分解,其數值計算具有較強的魯棒性,用SVD分解代替Cholesky分解,計算容積點協方差矩陣,可以有效增強濾波更新的穩定性。

SVD分解的方法是,對于一個m×n維的實數矩陣A,可以分解為

A=UΛVT

(2)

式(2)中：U、V均為單位正交陣,分別稱為左奇異矩陣和右奇異矩陣；Λ僅在主對角線上有值,其余元素均為0,一般形式表示為

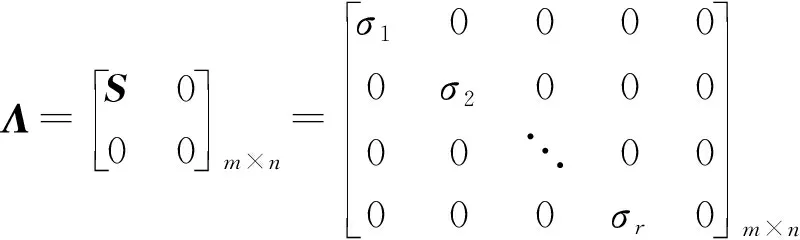
(3)

式(3)中：S=diag(σ1,σ2,…,σr)為奇異值矩陣,且σ1≥σ2≥…≥σr≥0,r為矩陣S的秩。

1.3 抗差方法

觀測信息在不斷參與更新過程,異常的觀測值會嚴重影響濾波結果,需要引入抗差因子減小異常觀測值對CKF濾波過程的干擾[20],當觀測信息精度高時,加大觀測值在狀態估計中的權值；反之,當觀測信息誤差偏大時,降低觀測值在狀態估計中的權重。

類似IGGIII等價權函數模型,將觀測殘差值進行分類,分為3個等級進行篩選,分別對應3種不同的抗差因子,即

(4)

式(4)中：k0、k1為常值,通常選取k0=1.5～2.0,k1=3.0～8.5；sv為標準化殘差[21]。這里要注意的是,抗差因子不能設置為0,否則可能影響觀測向量協方差矩陣的迭代更新。

1.4 改進的抗差SVD-CKF算法

考慮一個非線性系統:

xk=f(xk-1)+ωk

(5)

zk=h(xk)+vk

(6)

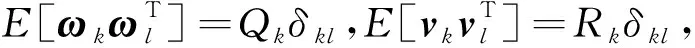
改進的抗差SVD-CKF算法步驟如下。

1.4.1 狀態參數初始化

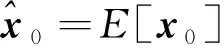
(7)

(8)

1.4.2 時間更新過程

使用SVD分解代替傳統Cholesky分解,對協方差矩陣Pk-1|k-1進行分解,并計算容積點Xi,k-1|k-1。

(9)

(10)

通過狀態方程來傳播容積點：

(11)

預測狀態值：

(12)

式中：m為容積點集矩陣的列數,通常為狀態維數n的2倍；ωi為容積點相應的權值,平均分配權值為ωi=1/2n。

預測協方差矩陣：

(13)

1.4.3 量測更新過程

對時間更新過程中求得的協方差矩陣進行SVD分解,并計算容積點：

(14)

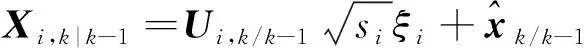
(15)

通過量測方程來傳播容積點：

Zi,k|k-1=h(Xi,k|k-1)

(16)

加權求和預測量測值：

(17)

使用均值濾波后的觀測值計算殘差值：

(18)

標準化觀測殘差值：

svk=yi,k/σi,k

(19)

式(19)中：yi,k為殘差向量的第i個分量；σi,k為其標準差。

預測觀測協方差矩陣,這里要根據觀測殘差值引入抗差因子rk,對觀測噪聲方差陣進行修正，即

(20)

預測互協方差陣：

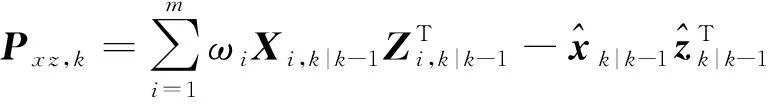
(21)

1.4.4 濾波更新

計算卡爾曼濾波增益：

Kk=Pxz,k/Pzz,k

(22)

利用先驗估計值和均值濾波后的觀測值進行狀態估計更新：

(23)

進行協方差矩陣更新：

(24)

算法的具體流程如圖2所示。

圖2 改進的抗差SVD-CKF算法流程Fig.2 Flow chart of improved robust SVD-CKF algorithm

2 運動模型建立

2.1 狀態方程

本文的算法應用于基于GPS導航的智能割草機平臺,首先需要建立模型來描述其運動狀態。由于割草機主要在平面草地上工作,其滾轉角和俯仰角可近似為0°,只考慮其在水平平面內的運動狀態,其主要運動狀態為勻速直線運動,因此以東向位置xe,東向速度ve,北向位置xn,北向速度vn作為狀態變量來建立狀態方程,k+1時刻的狀態可由k時刻的狀態得到,可以得到如下的狀態方程:

(25)

式(25)中：δ為過程噪聲；Δt為采樣時間間隔。狀態方程反應了不同時刻下狀態量之間的相互關系,其可簡單地表示為

X(k+1)=FX(k)+Q(k)

(26)

式(26)中：X為狀態量；F為狀態轉移矩陣；Q為系統噪聲矩陣。

2.2 量測方程

量測方程是針對GPS導航系統量測過程的模型假設,GPS所獲得的量測值有緯度L,經度λ,對地航速v,對地航向α。GPS所測得的原始位置坐標處于地理坐標系,需將其轉換到東北天坐標系,在考慮地球偏心率e不是很大的情況下,可以近似用以下公式進行轉換，即

(27)

式(27)中：a為地球的長半徑；ΔL為當前位置點與起始點的緯度差；Δλ為當前位置點與起始點的經度差。同時,也需要將GPS所測得的速度轉換到東北天坐標系,整合后的量測方程為

(28)

式(28)中：ε為量測噪聲；v為測得的載體對地航速；α為載體坐標y軸與正北方向的夾角,范圍為0°～360°。量測方程可簡單地表示為

Z(k)=HX(k)+R(k)

(29)

式(29)中：Z為觀測量；H為量測矩陣；R為量測噪聲矩陣。

3 仿真結果與分析

研究的GPS系統運用于割草機平臺,該平臺主要進行U字形自主作業,需要保證直線段勻速運動的位置準確性。為了驗證算法的可行性,采用MATLAB進行仿真分析。假設GPS平臺的采樣頻率為5 Hz,選取一段采樣時長為100 s的勻速直線運動段,其對地航速v=0.15 m/s,對地航向角α=75.7°。以此運動狀態為真實值,以東向位置、北向位置、東向速度和北向速度為狀態量進行分析,驗證算法的有效性。

3.1 抗差SVD-CKF濾波效果分析

由于在狀態轉移和量測的過程中存在噪聲的不確定性,在位置真實值上引入一組均值為0,方差為0.01的高斯白噪聲,在速度真實值上引入一組均值為0,方差為4×10-4的高斯白噪聲,以此來作為GPS系統采集處理后的觀測值。圖3和圖4所示分別為經過傳統CKF濾波后的位置和速度誤差,圖5和圖6所示分別為經過抗差SVD-CKF濾波后的位置和速度誤差。可以看出，經過傳統CKF濾波后的誤差相較于原始誤差值波動幅度有所減小,但是波動仍然較為劇烈；經抗差SVD-CKF濾波后的誤差值明顯平緩,說明其狀態估計更具穩定性。

圖3 傳統CKF濾波后位置誤差Fig.3 Position error after traditional CKF filtering

圖4 傳統CKF濾波后速度誤差Fig.4 Velocity error after traditional CKF filtering

圖5 抗差SVD-CKF濾波后位置誤差Fig.5 Position error after robust SVD-CKF filtering

圖6 抗差SVD-CKF濾波后速度誤差Fig.6 Velocity error after robust SVD-CKF filtering

兩種算法的誤差統計對比結果如表1所示,抗差SVD-CKF算法的標準差均優于傳統CKF算法,經抗差SVD-CKF算法濾波后的數據具有更平穩的性能。

表1 傳統CKF和抗差SVD-CKF的標準差比較Table 1 Standard deviation comparison between traditional CKF and robust SVD-CKF

3.2 改進的抗差SVD-CKF抗差效果分析

為了更好地驗證改進的抗差SVD-CKF算法在減小異常觀測值干擾的效果,考慮到GPS系統在失鎖時沒有信號,數據傳輸異常的情況以及割草機平臺打滑導致速度突變的狀況,以東向位置和東向速度為例,人為地在數據中加入異常觀測值,加入異常后如圖7所示。

圖7 東向加入異常后觀測值Fig.7 Observation after adding anomalies to the east

(1)位置異常:在東向位置觀測值10、25、70 s處加入2 m的觀測粗差。

(2)速度異常:在東向速度觀測值20 s處加入0.5 m/s的觀測粗差,在55 s處加入-0.2 m/s的觀測粗差。

在仿真實驗中,均值濾波選取的窗口長度N=5,抗差方法中的閾值選取k0=2,k1=4。加入異常觀測值后,其經過傳統CKF算法處理和改進的抗差SVD-CKF算法的處理后,異常點處的誤差值如表2所示,東向位置誤差和東向速度誤差對比如圖8所示。

圖8 傳統CKF和改進抗差SVD-CKF處理結果對比Fig.8 Comparison of traditional CKF and improved robust SVD-CKF processing results

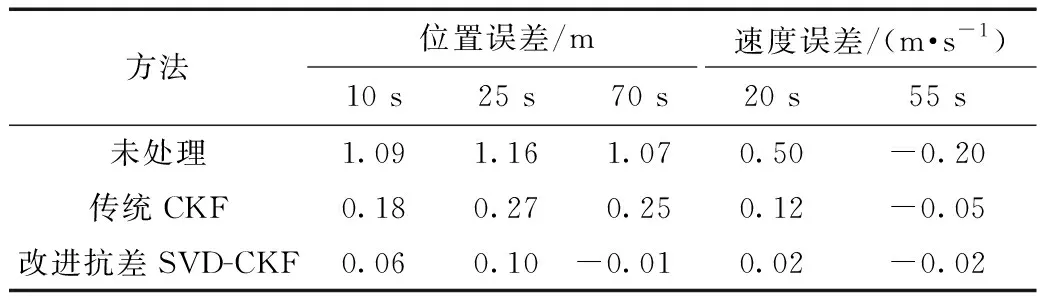
表2 異常點處誤差比較Table 2 Comparison of errors at abnormal points

可以看出,傳統CKF算法對于異常觀測值有一定的抑制效果,但是在出現異常時,產生的誤差波動仍然較大；改進的抗差SVD-CKF算法在初始狀態波動較大,運行一段時間后,即使遇到異常觀測值,也能迅速回到一個較為平穩的狀態,其對異常觀測值的校正能力相對傳統CKF算法要更強。

放大速度誤差0～40 s時間段的濾波處理結果如圖9所示。

圖9 0～40 s東向速度誤差對比結果Fig.9 0～40 s east speed error comparison result

由于有均值濾波預處理,當遇到異常觀測值時,濾波器可以及時作出響應,同時減弱大幅異常觀測值的干擾,減小了數據的波動性,使其能較快恢復到平穩的狀態,保證了后續迭代運算的準確性。而沒有經過均值處理和抗差算法處理的CKF算法,雖然一定程度上對異常觀測值有修正效果,但是需要較長的時間恢復到穩定狀態。

4 結論

提出一種改進的抗差SVD-CKF算法,經過仿真分析得到以下結論：

(1)均值濾波預處理對異常觀測值有較好的抑制作用,能及時降低異常觀測值所帶來的影響。

(2)SVD分解有效避免了先驗協方差矩陣負定導致濾波發散的情況,增強了濾波穩定性,保證了濾波器的持續運行。

(3)改進的SVD-CKF算法相較于傳統CKF算法有效降低了觀測數據的波動性,狀態更新值保持在一個相對穩定的狀態,能夠提高GPS導航的精度。