基于PID的制造業多智能體系統一致性分析

張忠藝，徐冬梅

（上海工程技術大學 電子電氣工程學院，上海 201620）

0 引言

為了優化特定的目標功能，調度可以定義為“如何根據時間來調度機器和資源”[1]。由于現代生產調度具有復雜性，特別是不確定性、動態性、復雜性等因素的綜合作用，使得現代制造系統的調度更加困難，導致生產任務動態變化的運行環境不確定性增加，要求調度系統具有較強的自適應性、魯棒性和可擴展性。

針對制造業的多智能體系統的分析方法主要有頻域法和Lyapunov函數法。頻率域法適用于單輸入單輸出系統，利用穩定性準則可確定系統上界的時延[2]；對一般線性系統來說，Lyapunov函數法更適合[3]。Lyapunov方法是用來分析系統的穩定性的時間域方法。其具體步驟是構造Lyapunov Krasovskii和Lyapunov Razumikhin函數，通過建立的Lyapunov函數，得到系統的時滯在一定范圍內波動的一致性充分條件，大部分文獻都要求解時滯上界。系統理想的通信方式是無延遲，時間域法將一致性問題轉化為系統誤差的漸近穩定問題，建立Lyapunov函數的線性矩陣不等式，得到系統的控制參數和控制條件。這種方法的研究對象大多是針對一級或二級多智能體系統，而對制造部門而言，其研究對象多是常階線性時變系統，該方法在應用過程中較為困難。針對這一問題，針對制造業多智能系統，提出了基于PID的一致性分析方法，通過狀態分解把一致性問題轉化為降階系統的穩定性問題，給出了系統一致性的充要條件，最后通過實驗驗證了所提方法的有效性。

1 制造業多智能體系統分析

多代理系統理論是分布式人工智能領域的一個重要研究方向，其基本思想是將一個大型的復雜系統轉化為能夠相互交流、相互協調的小型自治系統。制造業多智能體系統模型如圖1所示。

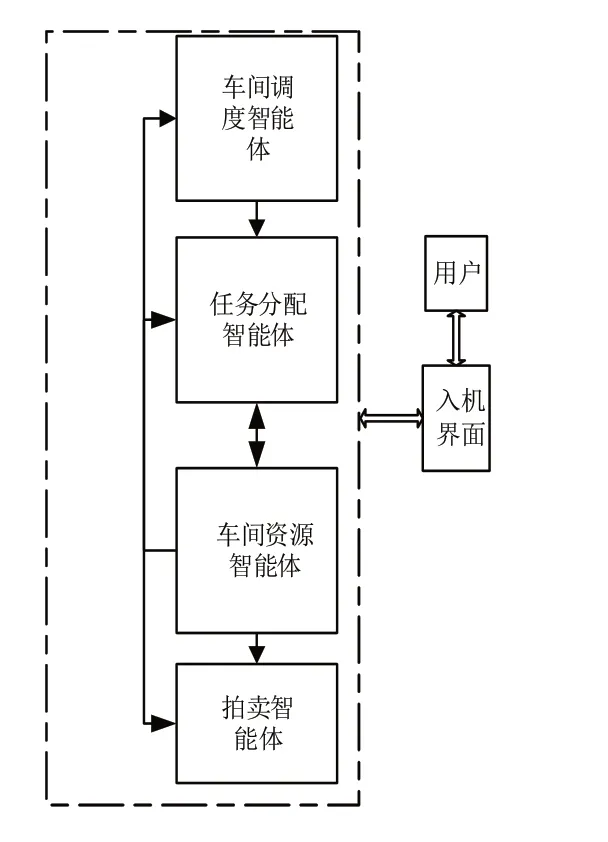
圖1 制造業多智能體系統模型

由圖1可知，制造業多智能體系統由車間調度agent、任務分配agent、車間資源agent和拍賣agent四個agent組成。將調度任務輸入系統后，制造業多智能體系統通過上述四個agent協同完成任務后輸出相應的調度結果[4]。

1）車間調度agent

車間調度agent用來接收外部過程輸入，判斷任務是否能夠完成，如有可能，車間調度代理將直接向任務代理分配操作，并安排最終輸出作業[5]。

2）任務分配agent

任務分配agent用來將車間調度agent接收任務的流程分解成子任務，每個任務的處理時間和成本在車間調度agent中進行查詢，并通過拍賣代理協調任務之間的沖突[6]。

3）車間資源agent

車間資源agent為所有可在現場執行的資源和任務提供信息，幫助拍賣agent提出最終工作計劃建議[7]。

4）拍賣agent

拍賣智能體用于處理制造業調度系統中加工工序、任務處理的沖突，因此拍賣agent也是制造業調度系統的核心。制造業調度系統是通過合理安排每項調度任務，實現總損耗最小、加工時間最短等最佳目標。根據拍賣協議，以目標參考變量為基礎對拍賣任務進行排序，以獲得最優的拍賣結果[8]。

2 預備知識

多智能體系統的研究中，通常將各智能體視為一個節點，結合PID法可簡化整個系統：

對由各個代理構成的多代理系統，可用圖G={V，ε}表示其網絡拓撲結構。拓撲學中的節點用非空的有限集合N={N1，N2，…，Nn}來表示，拓撲中的每條邊用一對節點表示[9]。

在有向圖中，定義一對節點（Ni，Nj）的邊即代理可以接收節點狀態信息；而在無向圖中，定義一對節點（Ni，Nj）的邊即智能體i、j可以互相接收并發送狀態信息，其他可通過定義的邊連接的節點稱為區域節點[10]。

為更直觀地了解PID控制與多智能體系統的關系，需要對網絡拓撲進行鄰接矩陣描述[11]。鄰接矩陣定義如下：

其中：

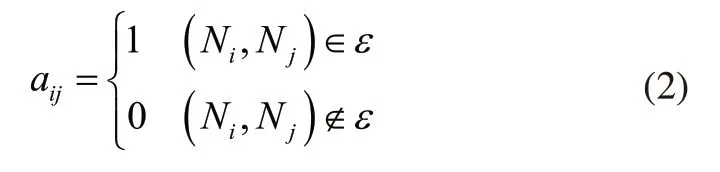
在有向圖中，當aij=1時，連接兩個節點Ni與Nj時，智能體j能夠接收代理的狀態信息，但是智能體i代理不能接收[12]。當aij=0時，兩個節點Ni與Nj之間沒有連接時，智能體i和智能體j之間均無法接收代理的狀態信息；

在無向圖中，當aij=1時，連接兩個節點Ni與Nj時，智能體i和智能體j之間可以自由接收各自狀態信息；當aij=0時，兩個節點Ni與Nj之間沒有連接時，智能體i和智能體j之間無法接收對方狀態信息。因此可以看出，無向網拓撲的鄰接矩陣是對稱的，而有向網拓撲則不一定對稱[13]。

實現PID控制前需要了解強連通圖、生成樹和有結點有向圖等概念知識，有向圖包含有向生成樹，即通過有向路徑中至少一個節點可以遍歷所有其他節點。對于無向圖，如果是連通圖則包含無向生成樹，如果是強連通圖則被定義為任意兩個結點之間的雙向路徑[14]。因此有向圖中存在有向生成樹并不一定意味著圖是強連通的，但是有向生成樹是存在于強連通圖中的。

3 基于PID控制的一致性分析

3.1 PID參數設計

在系統不穩定的情況下，PID參數設計過程中，首先需要滿足式(1)；然后利用LMI工具箱結合定理1求解制造業調度系統所需要的增益矩陣K1和K2。根據制造業調度系統所處條件的不同，PID參數設計過程中存在以下兩種情況：

1）若無噪音，則該系統為穩定系統，即各agent應一致振動。采用遺傳算法求解PID參數，以跟蹤誤差、上升時間和控制能量作為系統優化指標。在此基礎上，選取了一個基于經驗的PID調整參數，并將其剩余參數等調整參數與原始數據進行比較，從而確定最優調整參數，從而使系統具有較好的收斂性能[15]。

2）假設制造業調度系統存在隨機噪聲，證明了系統處于不穩定狀態，然后用PID參數選取適當的經驗值，并將PID控制與純比例控制相比較，說明PID控制對系統噪聲的具有抑制作用。

3.2 一致性分析

圖2是包含6個節點的有向圖，第1節是根節點，從區段1開始，其可以指向其他五個節點，其中有一個樹是由其直接生成的。但是節點2、3、4、5、6不能通過有向路徑遍歷其他所有節點，因此圖中沒有實現強連通。

定理1：當有向圖存在有向生成樹時，其對應的PID控制矩陣只是零特征值，其他非零特征值均位于右半平面。

定理2：若圖中僅存在一棵生成樹，則圖中所對應的多主體系統將逐漸收斂。

通過以上定理可知，相應的PID控制矩陣具有唯一的零特征值，其特征值對應的特征向量為0，其他非零特征值放置在右平面上，即特征值的實部為正。

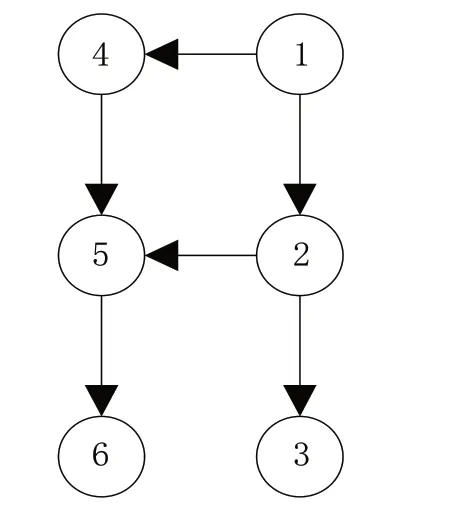
圖2 含有六個節點的有向圖

由于PID控制矩陣L存在唯一一個零特征值，故Rank（L）=n-1。網絡拓撲的代數連通度是PID控制矩陣的最小非零特征值λ2（L）。

最小非零特征值λ2（L）與算法收斂速度成正比例關系，當λ2（L）變大，則說明算法收斂速度也隨之變快；當系統出現時滯問題時，需要將最小非零特征值λ2（L）與時滯大小對比，由此避免時滯給系統運行帶來的干擾。圖3為含有四個節點的有向圖。

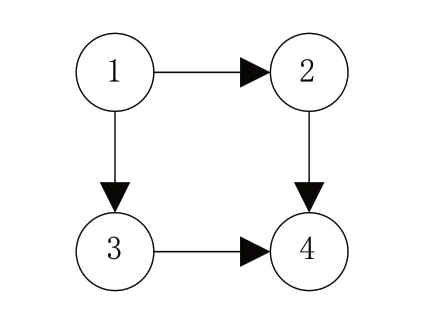
圖3 含有四個節點的有向圖

圖3的四個節點有向圖中對應的鄰接矩陣的入度Q與出度W為：

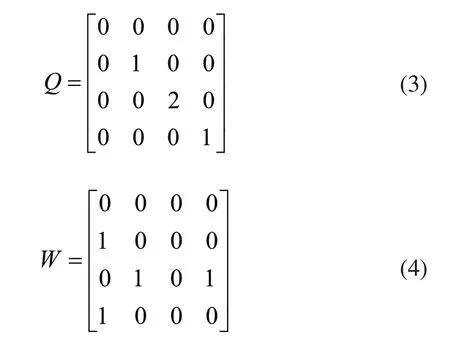
結合式(3)、式(4)，構建PID控制矩陣為：

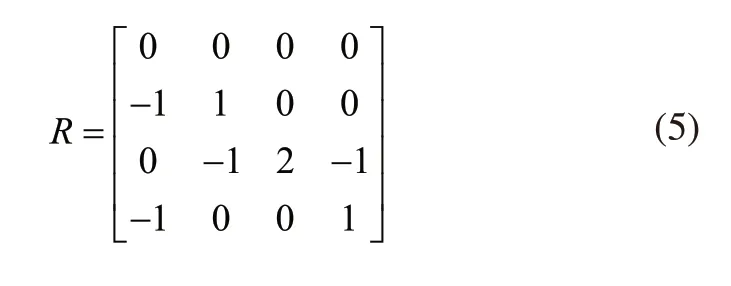
根據式(5)的PID控制矩陣，可確定特征值為，λ1=0，λ1=λ3=1，λ4=2。

定理1驗證：通過極點配置智能體系統矩陣，確定PID參數，通過求解不等式，確定增益矩陣K1，驗證結果如圖4所示。

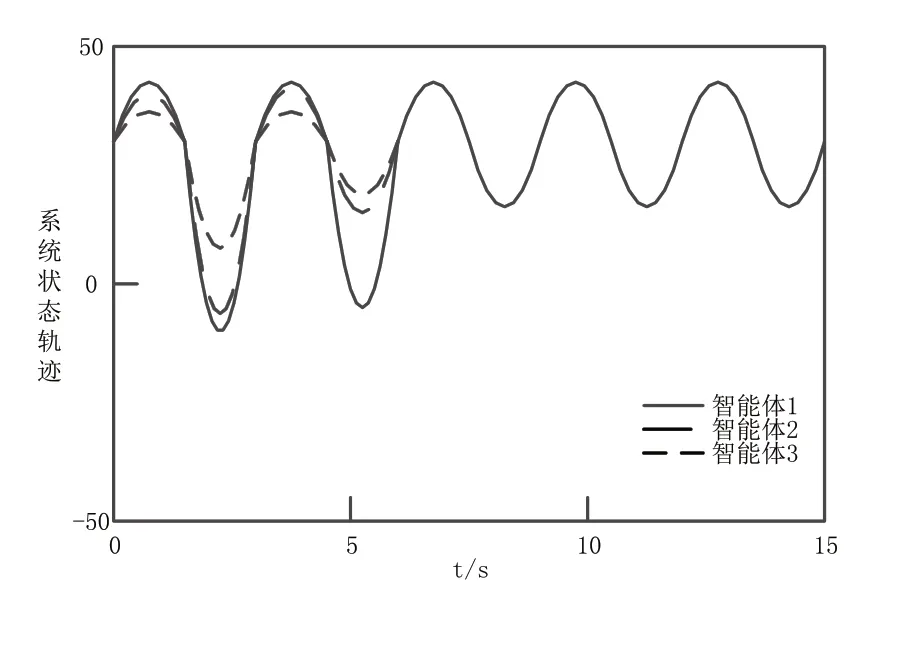
圖4 定理1驗證結果

由圖4可知，雖然在不同PID控制矩陣的特征值下，多智能體系統狀態沒有趨近于0，但最終趨近于一致，使用PID控制方法可以快速消除系統余差，加快系統一致性收斂。

定理2驗證：假設系統存在噪聲，在該情況下確定PID參數，通過求解不等式，確定增益矩陣K2，驗證結果如圖5所示。

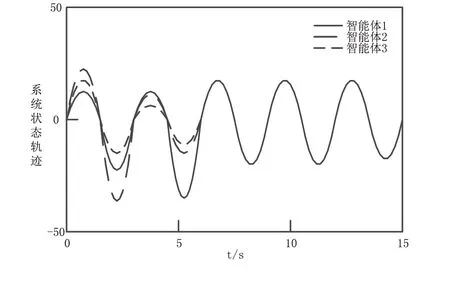
圖5 定理2驗證結果

由圖5可知，在制造系統存在隨機干擾噪聲的情況下，采用PID控制方法，可以迅速消除系統余差，實現系統一致性。

4 實驗

為了驗證基于PID的制造業多智能體系統一致性分析合理性，進行實驗驗證分析。

4.1 智能體車間調度設置

如圖6所示為多智能體車間調度過程示意圖。

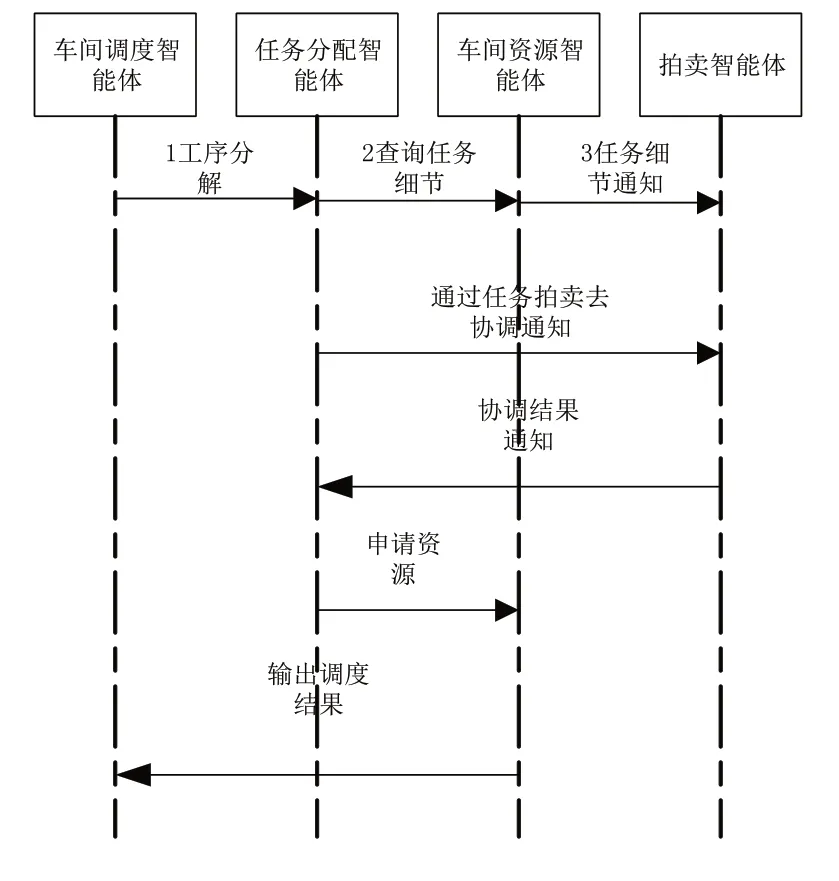
圖6 多智能體車間調度過程

如圖6所示，多智能體車間調度過程主要有5個步驟：

1）車間調度代理接收處理任務，由程序模塊判斷是否可以完成任務。不能完成任務時輸出“工序超限”命令，可以完成任務時則向代理傳送工序通知任務；

2）任務分配代理將接收到的工序分解成若干個子任務，并向車間資源代理查詢其消耗、工時、成本、廢物處理等任務；

3）車間資源代理向拍賣代理傳遞任務細節；

4）任務管理通過信息將所收到的任務傳送給拍賣代理，二是拍賣代理能夠協調任務沖突；

5）拍賣行根據預定的目標函數協調需要拍賣的沖突，比如在最短處理時間等情況下，協調的結果將作為任務分配給單個智能體。

4.2 實驗結果與分析

制造業多智能體相應的接近中心性和最小-最大距離中心性如表1所示。

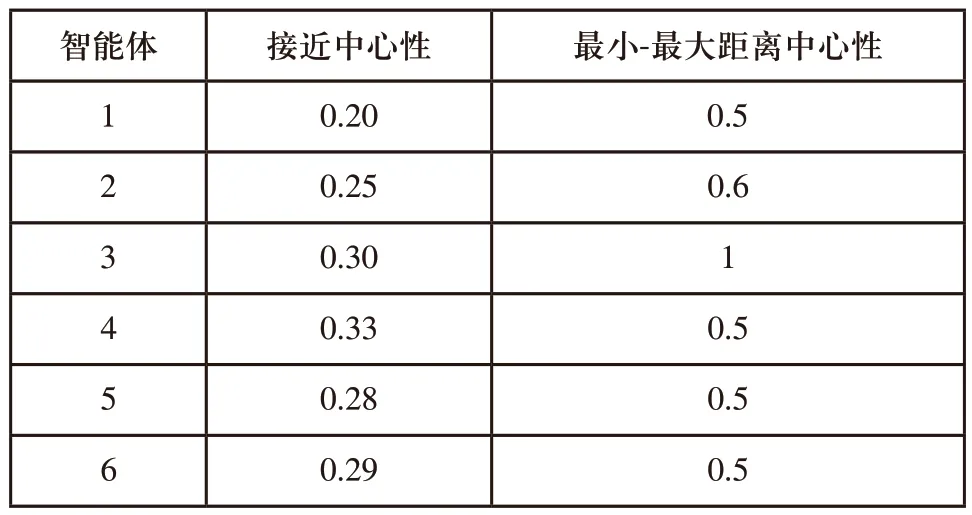
表1 制造業多智能體相關參數

在表1所示的相關參數下，分別使用頻域法、Lyapunov函數法和基于PID分析方法對系統狀態軌跡一致性進行驗證，對比結果如圖7所示。

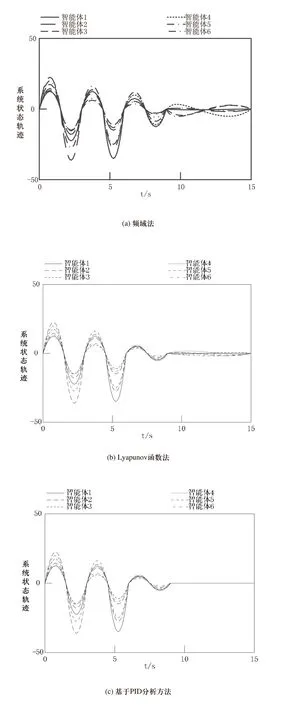
圖7 不同方法系統狀態軌跡一致性驗證分析

由圖7可知，使用頻域法6個智能體系統狀態軌跡在10s時間內，曲線稍有收斂，但在15s以內收斂逐漸停止，達不到一致性效果；使用Lyapunov函數法6個智能體系統狀態軌跡在10s時間內，曲線相較于頻域法收斂程度更高，但在15s以內依舊達不到一致性效果；使用基于PID分析方法6個智能體系統狀態軌跡在10s時間內，曲線收斂速度較快，在15s以內能夠達到一致性效果。由此證明，所提方法收斂性較好，能夠達到系統多智能體一致性效果。

5 結語

為了解決任意階線性連續時間多智能體系統中所存在的不足，提出基于PID的制造業多智能體系統一致性分析。首先將系統一致性問題轉化，然后通過PID控制矩陣給出制造業多智能體系統在有向圖拓撲中存在唯一全局可達節點這一充分條件，以達到一致性。通過實驗可以得出所提方法有著良好的可行性及有效性，但是由于實驗的智能體數量較少，未來隨著數量增加算法會越來越多，需要進行更深層次的研究。