基于改進的BPSO算法的關聯規則挖掘
(江南大學 無錫 214122)
1 引言
關聯規則指數據庫中超過指定最小支持度和最小置信度的項目的集合,作為數據挖掘的重要組成部分它一直是學者的研究熱點[1]。隨著挖掘問題變得越來越復雜,諸如Apriori算法與FP-growth算法等傳統算法出現了缺點,其中最典型的是由大量候選項集和復雜的數據結構所造成的時間和內存的成本,導致挖掘效率較低[2]。因此許多學者開始使用啟發式算法,粒子群優化算法(PSO)是應用較為廣泛的算法之一[3]。
有許多研究將啟發式算法應用于關聯規則挖掘。例如,Chen等使用PSO算法從高維數據集中挖掘關聯規則[4],Rom提出的基于遺傳算法的關聯規則可避免挖掘過程中發現的無用個體[5],BADA等融合了PSO算法和蟻群算法(ACO),將事務數據轉換為二進制數據后,從數據集中挖掘頻繁項集[6],Kuo等使用PSO算法快速有效計算出關聯規則的最小支持和置信度[7]。
然而,大多數改進的PSO算法重點考慮粒子全局和局部搜索能力,而忽略了粒子種群和搜索范圍帶來的影響。因此,本文提出了一種改進的二進制粒子群優化算法(GRBPSO),根據適應度函數對粒子初始種群進行預處理,并以頻繁項集的性質為依據對粒子搜索空間進行縮減,減少算法運行時間。
2 基本概念
2.1 頻繁項集
頻繁項集的有關定義為I={i1,i2,…,im}是m個不同項目的集合,每個ik稱為一個項目[8]。數據集D={t1,t2,…,tn}是n個不同事務的集合,每個tk稱為一個事務,其中tk?I。集合X?I稱為項集,|X|表示項集中的項目數,長度為1的項集稱為1項集。項集X的支持度表示為sup(X),其含義是項集X在數據集D中出現的實際頻率,若sup(X)≥最小支持度(min_sup),則稱項集X是頻繁項集。
頻繁項集挖掘的目標是根據給定的最小支持度(min_sup)挖掘出所有的頻繁項集。根據以上描述,可推出性質1。如下所示:
性質1:?Xi?X?sup(Xi)≥sup(X)
因此,當Xi?X時,若Xi不是k維頻繁項集的子集,則項集X也不是k維頻繁項集的子集。
2.2 關聯規則
關聯規則是形如A?B的蘊含式[10],其中A?I,B?I,并且A∩B=?。
一般使用三個指標來度量關聯規則,分別是支持度(support)、置信度(confidence)和提升度(lift)[11]。根據這三個指標可以篩選出滿足條件的關聯規則。
以A?B這個關聯規則為例來說明:
支持度(support):表示同時使用A、B的人數占所有用戶數的比例。如果用P(A)表示使用A的用戶比例,那么support=P(A&B)。
置信度(confidence):表示使用A的用戶中同時使用B的比例,即同時使用A和B的人占使用A的人的比例,即confidence=P(A&B)/P(A)。
提升度(lift):表示“使用A的用戶中同時使用B的比例”與“使用B的用戶比例”的比值,即:lift=(P(A&B)/P(A))/P(B),提升度反映了關聯規則中的A與B的相關性,提升度大于1且越高表明正相關性越高,提升度小于1且越低表明負相關性越高,提升度=1表明沒有相關性[12]。
2.3 二進制粒子群優化算法(BPSO)
PSO算法在實現過程中隨機選取一群粒子作為初始粒子群,搜索空間中的每個粒子都是一個可能解,算法通過迭代找到最優解。在算法迭代過程中粒子以兩個極值為依據來更新自己,第一個極值稱為個體極值,是粒子個體找到的最優解;第二個極值稱為全局極值,是整個種群目前找到的最優解。
離散二進制粒子群算法是J.Kennedy和R.C.Eberhart在1997年提出的[13]。PSO算法設計之初是為了優化連續函數的,但實際生活中待解決的問題大多是基于離散空間上的組合優化問題,因此提出BPSO算法以解決這一問題。
BPSO算法在離散粒子群算法基礎上,約定位置向量、速度向量均由0、1值構成[14]。粒子根據式(1)更新自己的速度,根據式(2)和式(3)更新自己的位置,式(2)為映射函數:
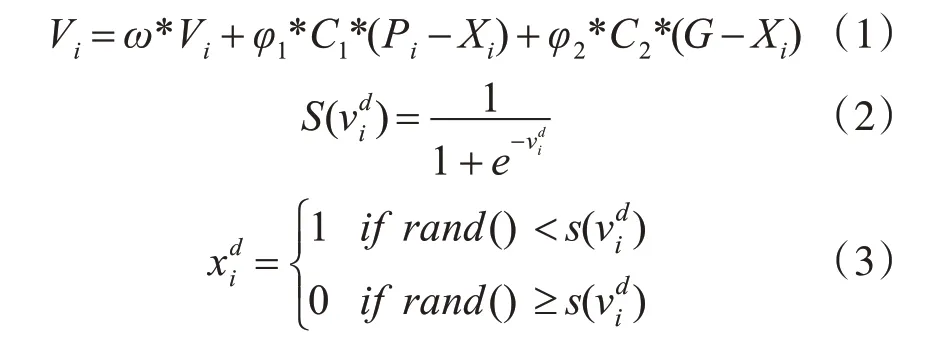
其中,Vi為第i粒子的速度,pi為個體極值,G為全局極值,ω為慣性因子,C1,C2為學習因子,φ1和φ2為[0,1]之間的隨機數。為在d維空間中第i個粒子軌跡當前為0的概率,為在d維空間中第i個粒子位置變化的絕對概率,rand()為[0,1]之間的隨機數。
3 GRBPSO算法
3.1 適應度函數
適應度函數是用來評價給出的候選解即粒子的好壞的[15]。在PSO算法中,適應度函數往往具有驅動粒子前進的作用,在搜索空間中指出粒子的前進趨勢。適應度函數的設計依賴于實際問題,針對不同問題,適應度函數的設計也不盡相同。
在關聯規則的研究中支持度是評價一組關聯規則是否有效的基礎指標。支持度代表了項目重復出現在一組事務數據庫中的次數。現實中數據庫內的數據往往具有多樣性和復雜性,為了在實際項目中挖掘有意義的關聯規則,本文算法將粒子出現的實際次數作為其適應度值,粒子的適應度函數如式(4)所示:
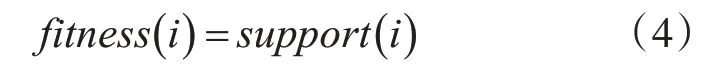
其中,support(i)為粒子種群中粒子的實際支持度也即實際出現頻率。
在GRBPSO算法中,個體極值指的是粒子群中各個粒子在此次迭代條件下的支持度,全局極值指的是在此次迭代條件下整個種群中全部粒子的最優支持度,算法在每次迭代中修改這兩個極值,假設某個粒子的個體極值不小于最小支持度,則將該粒子列為候選項集。
3.2 初始粒子群預處理
在頻繁項集挖掘過程中數據集中可能存在某些項目出現頻率較低的現象,這就可能導致隨機選取的粒子種群質量不高,進而影響挖掘結果及挖掘效率。在GRBPSO算法中,首先對初始粒子群進行預處理,保證一定比例的粒子具有合理的初始適應度。
對初始粒子群進行預處理的方式是將種群中出現頻率較低的粒子位置設置為0,首先以確保初始粒子群具有適當的適應度,提高初始種群的質量;同時在二進制數據集中也可減少粒子的數量和空間維數。在GRBPSO算法中,結合關聯規則的相關定義,可根據用戶設置的最小支持度值修改對應粒子的位置值,修改方式為若粒子的出現頻率即初始適應度值小于最小支持度,則將該粒子的位置更新為0。
3.3 縮減搜索空間
利用BPSO算法在大數據集中挖掘關聯規則意味著搜索空間較大,而搜索空間對算法運行效率有著重要的影響,因此,本文設計一種縮減搜索空間的優化策略,減少搜索空間,提高算法運行效率。
假設GRBPSO算法在發現頻繁項集階段,G為當前全局極值。在此期間,任一支持度小于G的項目將會被剪枝,即?i∈I,若sup(i)<sup(G),則項目i被剪枝。于是,?i∈I且sup(i)<sup(G),從性質1可知,?X?I且i∈X,可推出sup(X)<sup(G) 。也就是說,若項集中含項目i,則需更新該項集,將其中的項目i剪枝。
4 實驗及分析
為了驗證GRBPSO算法的正確性及有效性,本文對大量數據集進行了實驗,并給出在6個數據集上的實驗結果及分析比較。實驗環境為2.10GHz AMD R5 CPU,8G內存和Windows 10操作系統,算法在VS2015平臺上采用C++語言編程實現。數據集分別為Connect、Mushroom、Retail、Pumsb、Ko?sarak、BMS-POS,數據集下載地址為http://fimi.uantwerpen.be/data/。數據集展示如表1所示。
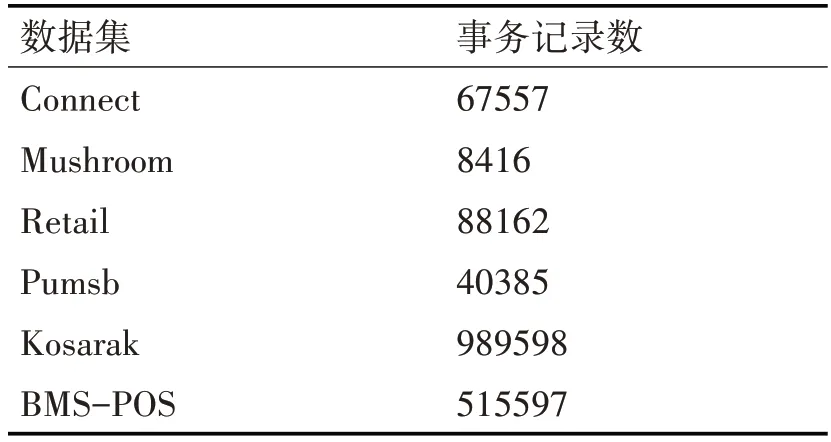
表1 實驗數據集
4.1 實驗一
在實驗一中,從種群規模方面對GRBPSO算法與BPSO算法進行比較。算法的參數設置為最大迭代次數N=10,慣性因子ω=0.2,學習因子C1=C2=1,粒子最大速度為2。算法中的最小支持度設置為0.3,最小置信度(min_conf)設置為0.6,最小提升度(lift)設置為4。實驗結果如圖1所示。
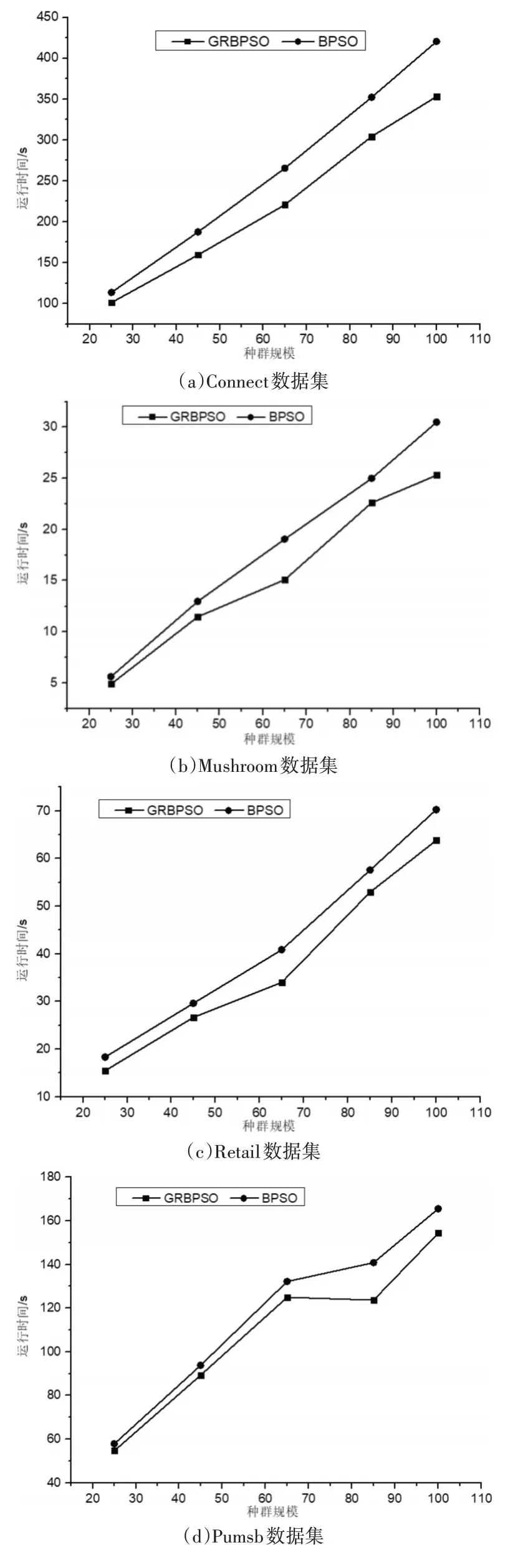
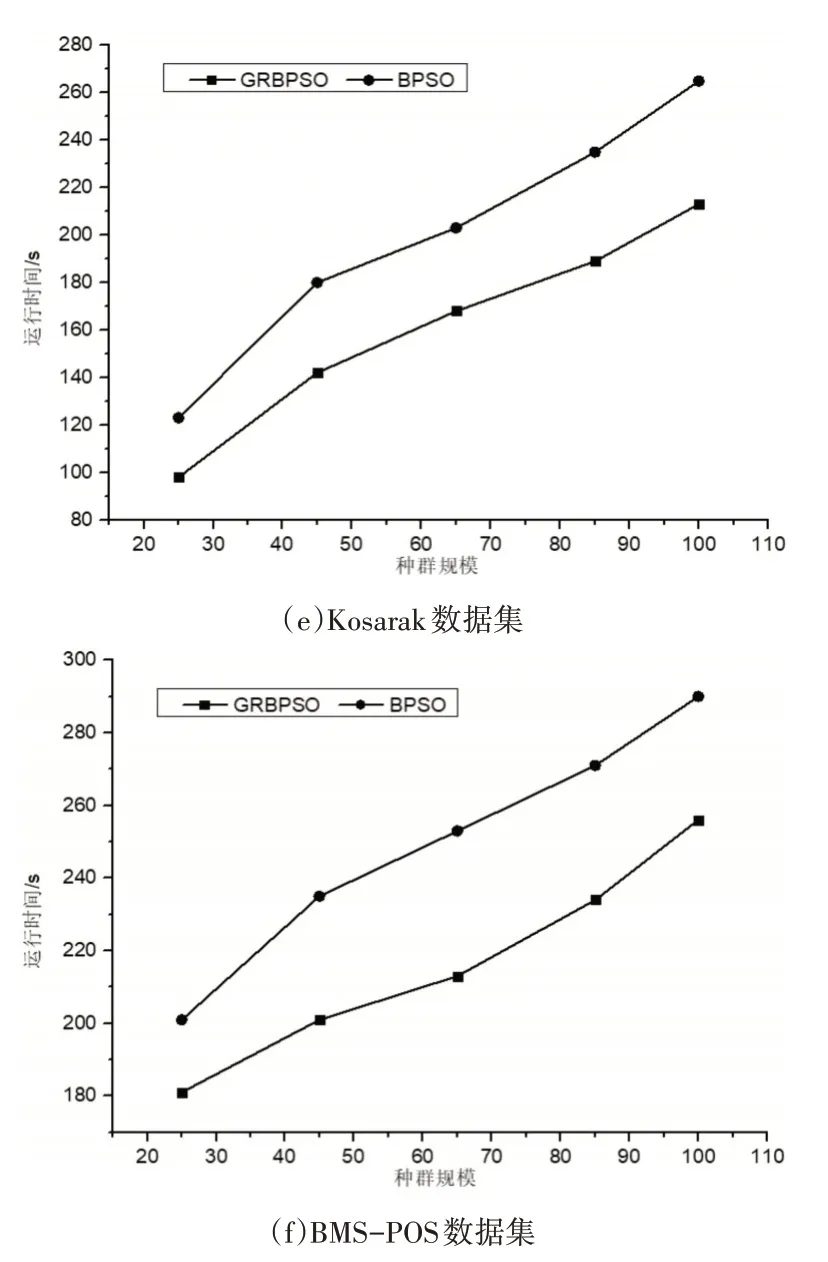
圖1 算法運行時間對比
圖1表示在種群規模為可變因素的情況下兩種算法在6個數據集上挖掘關聯規則的時間對比。由圖1可知,兩個算法在種群規模不斷增加的情況下,運行時間也隨之增加,原因是種群規模的擴大導致算法中對適應度的計算變得復雜,進而影響算法的運行時間。但由圖1可知本文算法的運行時間始終小于BPSO算法,并隨著規模變大這種優勢愈加明顯,因此充分說明本文算法在種群規模變化的前提下是高效的。
4.2 實驗二
在實驗二中,從迭代次數上對GRBPSO算法與BPSO算法進行比較。算法的參數設置為種群規模K=80,慣性因子ω=0.2,學習因子C1=C2=1,粒子最大速度為2。算法中的最小支持度設置為0.3,最小置信度(min_conf)設置為0.6,最小提升度(lift)設置為4。實驗結果如圖2所示。
圖2表示在迭代次數為可變因素的情況下兩種算法在6個數據集上挖掘關聯規則的時間對比。由圖2可知,兩個算法在迭代次數的不斷增加下,運行時間也隨之增加,并由圖2可知本文算法的運行時間始終小于BPSO算法,并隨著迭代次數的變多在部分數據集中這種優勢愈加明顯,因此充分說明本文算法在迭代次數變化的前提下是相對高效的。這是因為大數據集導致搜索空間變大,GRBPSO算法在對初始種群進行預處理時可一定程度地縮減搜索空間,并同時采用了優化策略對搜索空間進行裁剪,大大減少粒子的飛行空間,在一定程度上提高了關聯規則挖掘效率。
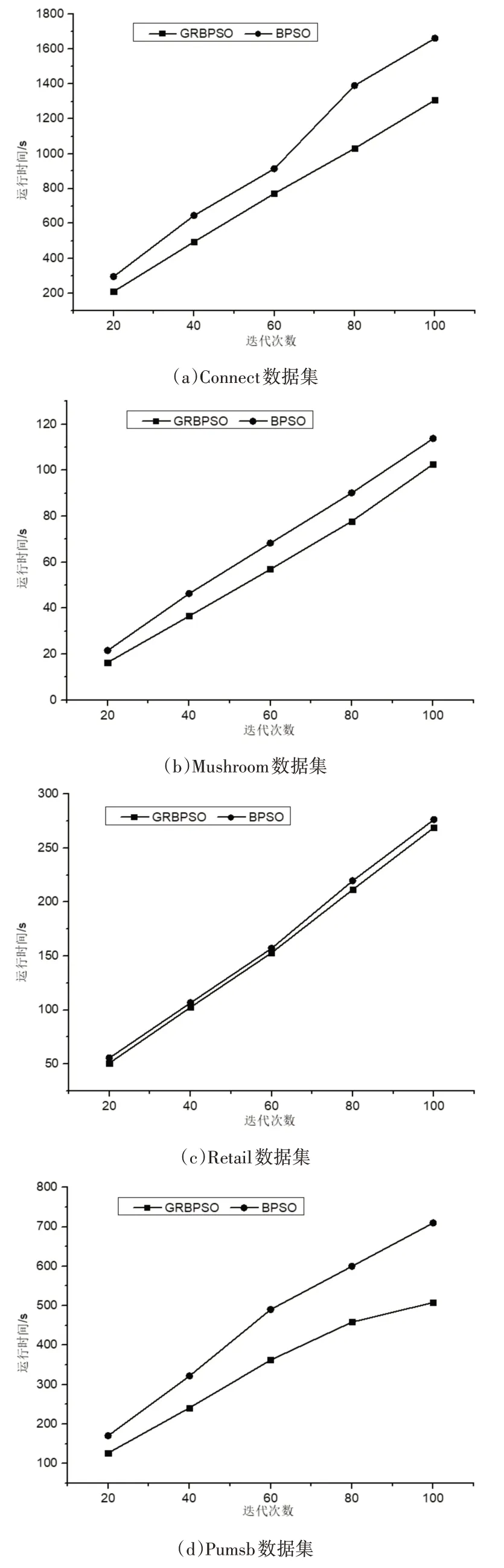
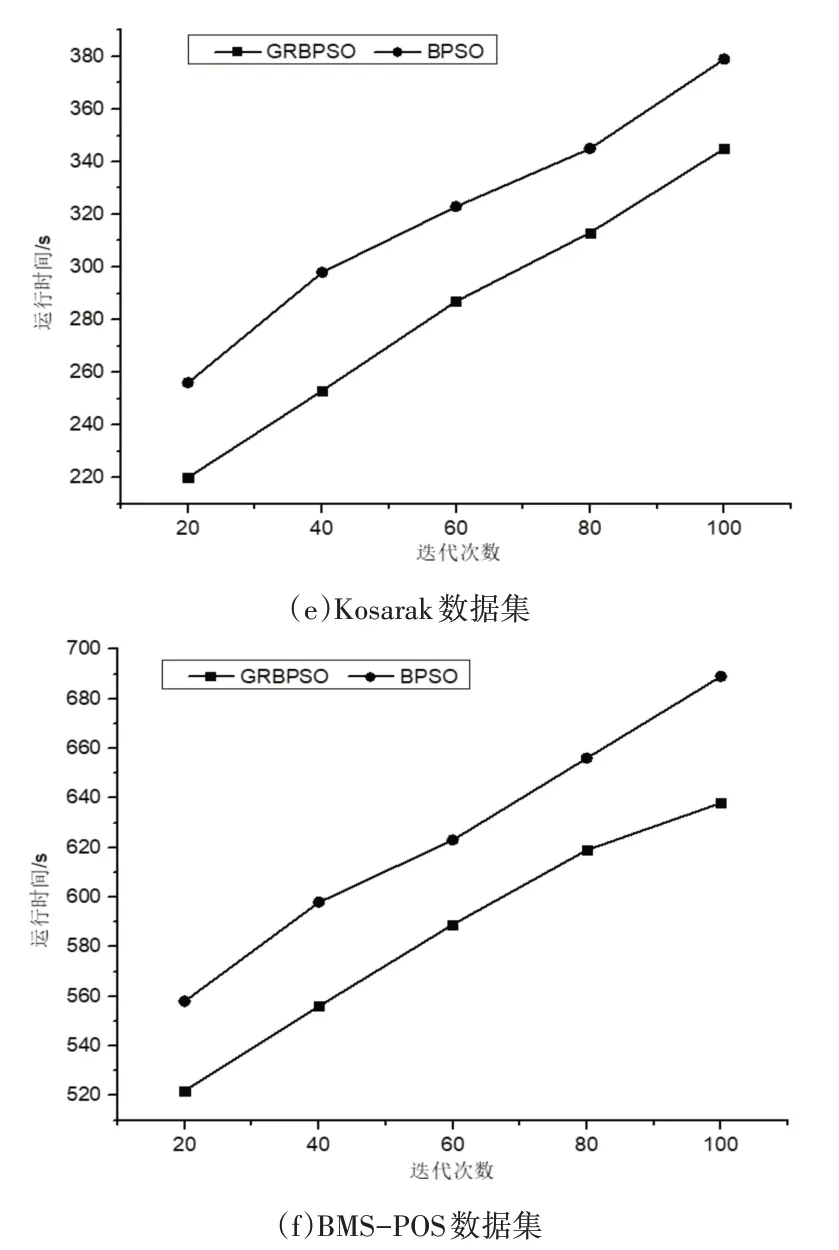
圖2 算法運行時間對比
4.3 實驗三
在實驗三中,比較GRBPSO算法與同類型算法的挖掘效果。本文以挖掘頻繁項集的數量作為參考值,同類型算法分別為PSOFIM算法[16]、GA-Apriori算法及PSO-Apriori算法[17]。根據文獻[17],表2中的對比算法均為在最優參數下算法挖掘的數量,本文算法的挖掘結果具有不確定性,原因是算法在初始種群的選擇上具有隨機性。為說明本文算法的可行性和穩定性,本次實驗在6個數據集中均重復10次,實驗的最終數據為10次實驗的平均結果。算法的參數設置為種群規模K=80,迭代次數N=20,慣性因子ω=0.4,C1=C2=1,Vmax=3,算法的最小支持度均為0.2,實驗對比結果如表2所示。
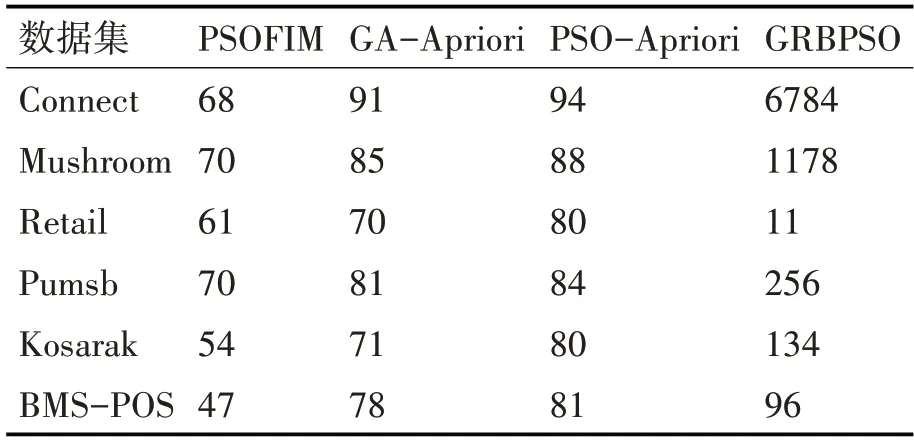
表2 各算法挖掘到的頻繁項集數量(/個)
由表2可知,以數據集Retail為例本文算法的頻繁項集挖掘數量少于其他同類型的3個算法,但在其他數據集中本文算法表現較為優越,尤其是在Connect數據集和Mushroom數據集中表現突出。在Retail數據集中本文算法挖掘數量少于其他3種算法是由Retail數據集的特征引起的,在Retail數據集中事務數據庫的平均長度較小且數據分布較為零散,數據集中事務屬性數較少,在進行頻繁項集挖掘時本文算法對初始粒子群的選擇是具有概率性的,因此在預處理過程中粒子位置為0的概率變大,導致挖掘結果不佳。但從整體來看,本文算法在大數據上挖掘頻繁項集是可行的,并且挖掘結果也是可觀的。
5 結語
本文提出了一種基于改進的二進制粒子群優化算法的關聯規則挖掘方法。首先結合實際情況,將粒子支持度作為GRBPSO算法的適應度函數;然后根據最小支持度對初始種群進行處理,提高初始種群質量;最后根據優化策略對搜索空間進行縮減。通過實驗證明,本文提出的GRBPSO算法在挖掘關聯規則上是可行的且高效的。

