基于斜盤交錯角的柱塞泵流量脈動研究?

（西南交通大學機械工程學院 成都 610031）

1 引言

為了降低斜盤式軸向柱塞泵的噪聲，必須減小來自泵源處的流量脈動和振動，控制流量脈動的關鍵因素在于配流盤的設計，配流盤上的腰形槽的開啟角度和關閉角度對流量脈動、柱塞腔沖擊力、斜盤力矩有著重要影響［1］。靠增加出口腰形槽的開啟角度，即形成預壓縮角，使柱塞在運動過程中對油液進行預壓縮，可以使柱塞腔與出口腰形槽連通時的油壓與出口壓力完美匹配，從而減少由油液壓縮性帶來的流量脈動［3］。但是預壓縮角的缺點在于對工況的高敏感性，即當出口壓力、轉速、排量角發生變化時，流量脈動將會增加，配流盤腰形槽不再是最優設計［2］。文獻［4］依靠旋轉配流盤的方法來調節配流盤的開啟角度［4］，使得預壓縮效果與工況相匹配，這種方法的缺陷在于實現成本較高而且需要外部設備進行實時調節，不便于推廣應用。而斜盤交錯角結構通過調節斜盤的交錯角來改變柱塞的運動規律，等效于旋轉配流盤且實現成本較低，是一種較好的降低流量脈動的方式。

如圖1所示，虛線表示柱塞泵斜盤的法向量，用來確定斜盤的空間朝向，傳統的斜盤轉動方向是繞Y軸旋轉，而交錯角結構的斜盤是先繞X軸旋轉交錯角α，斜盤法向量由OZ轉動到OA，再繞Y軸旋轉排量角β，斜盤法向量由OA轉動到OA'。通過兩次轉動使斜盤與配流盤之間形成一個錯配角，等效于旋轉配流盤改變柱塞的運動規律，從而影響柱塞在三角槽過渡區的壓縮體積，進而減小倒灌流量、降低流量脈動率［5～7］。

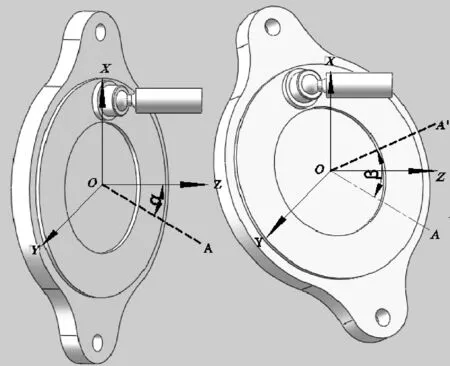
圖1 斜盤交錯角原理

2 柱塞的運動分析

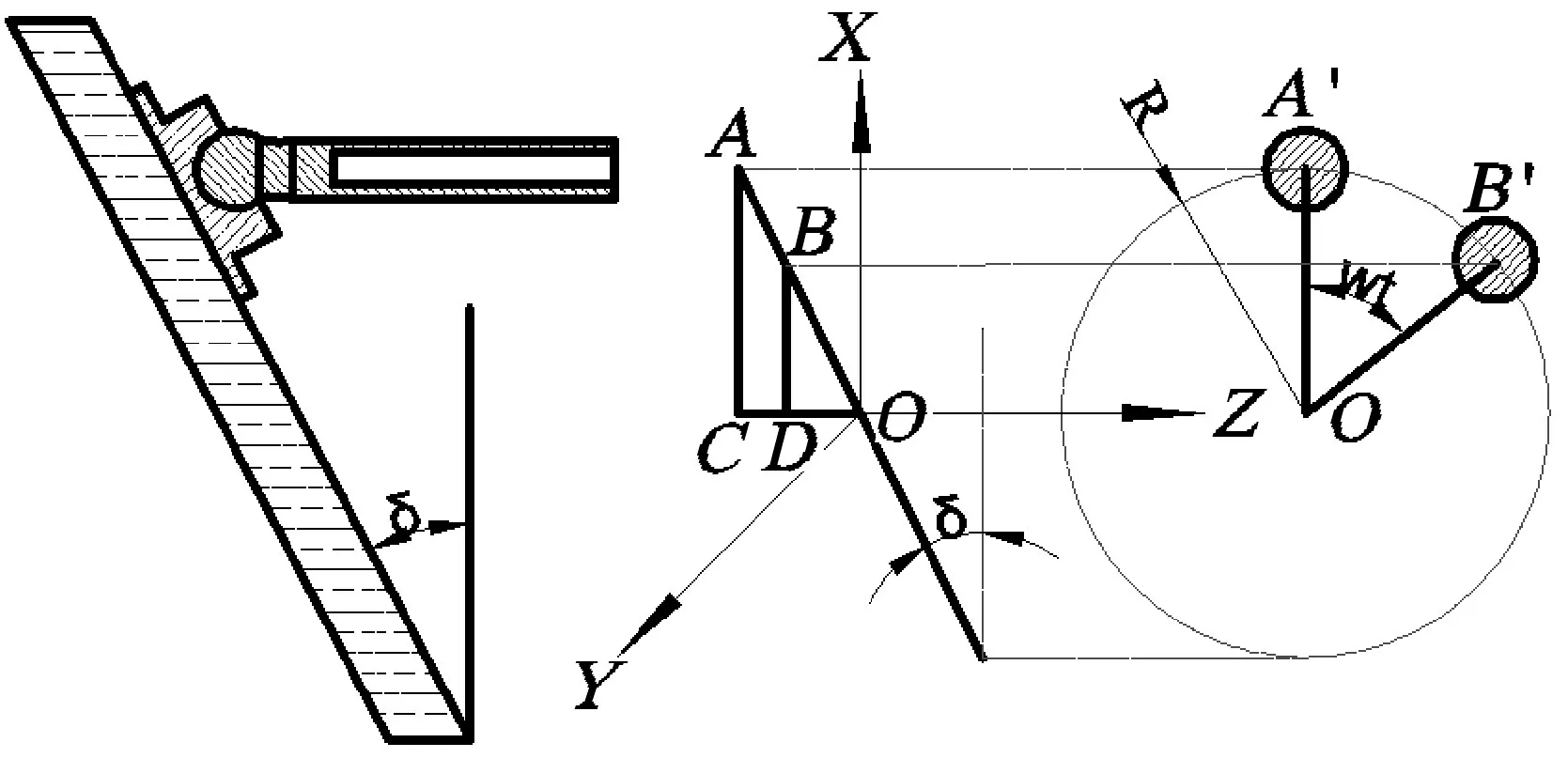
圖2 柱塞運動原理

要分析交錯角對柱塞運動的影響，首先要分析一般柱塞泵的柱塞運動規律，在此基礎上考慮交錯角對柱塞運動規律的影響。

如圖2所示，以斜盤的中心O點為坐標系原點、柱塞在X方向上的最高點A點為柱塞開始運動的起點，則柱塞的運動軌跡在X-Y平面上的投影是一個圓，該軌跡圓在X方向上的位移為

由于柱塞在Z方向上的位移與X方向上的位移成正比，比例為斜盤傾角的正切值：

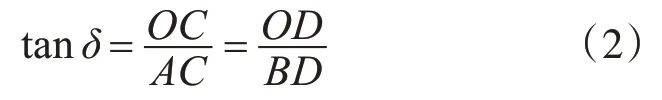
式中AC與BD是X方向上的位移，OC與OD是Z方向上的位移。

所以柱塞在Z方向上的位移即軸向位移等于X方向上的位移乘以tanδ，即：

該余弦函數的相位角為0，當且僅當斜盤的旋轉軸為Y軸時成立。若斜盤存在交錯角，則無法確保斜盤的旋轉軸是Y軸，斜盤可能繞X-Y平面內任意一根軸旋轉。如圖3所示，兩條相互垂直的虛線分別表示斜盤的死點軸和等效旋轉軸，斜盤的死點軸與配流盤的對稱軸之間錯開一個角度，即錯配角ε。由于柱塞運動的起始位置位于配流盤對稱軸，所以柱塞位移起始相位等于錯配角ε，交錯角柱塞泵的柱塞位移函數為

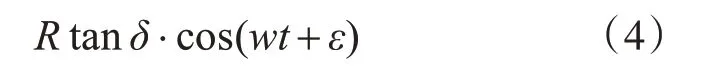
式中，R為柱塞分布圓半徑，mm；w為主軸轉速，r/min；δ為斜盤的有效排量角，°；ε為斜盤的錯配角，°。

式中Rtanδ是余弦函數的幅值，ε是余弦函數的相位角，只要能夠計算出有效排量角δ與錯配角ε就可以得出柱塞在軸向方向的運動規律，需要注意的是，此時的有效排量角δ不等于斜盤沿Y軸旋轉的排量角β，有效排量角δ是以斜盤交錯角α、排量角β為自變量的函數，同理錯配角ε也是以α、β為自變量的函數［8］。

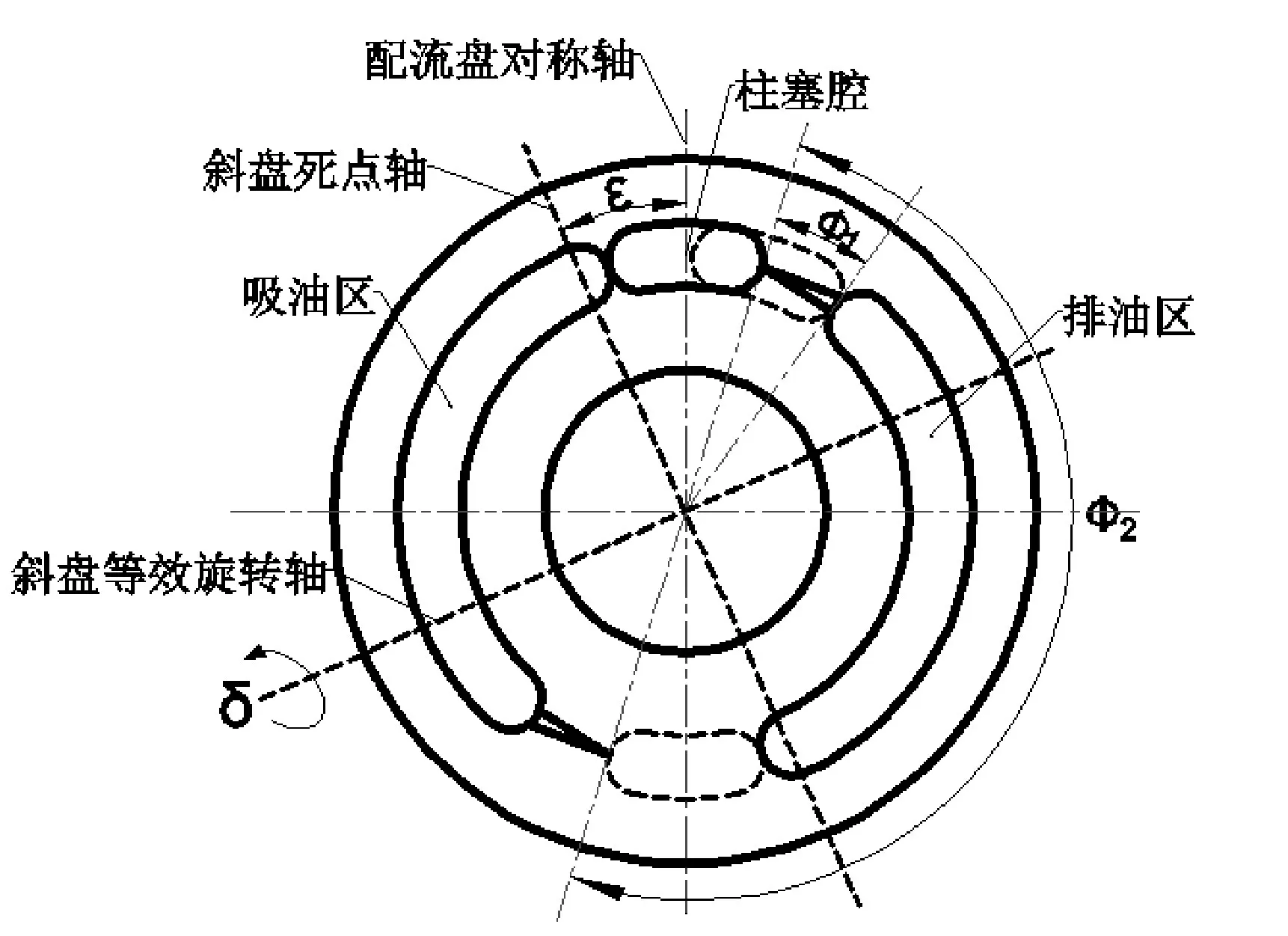
圖3 交錯角柱塞泵的柱塞運動規律

3 角度函數關系的幾何分析

如圖4所示，本文通過研究斜盤法向量的轉動過程得出有效排量角δ、錯配角ε與斜盤交錯角α、排量角β的函數關系，為了方便數學描述，本文把斜盤法向量的轉動過程放入到長方體內進行分析，假設O點為斜盤中心點，OZ為柱塞泵的主軸方向，初始斜盤法向量與OZ軸重合，斜盤法向量首先沿Y-Z平面轉動α，由OZ軸轉動到OA，再沿縱向平面XOA轉動β，由OA轉動到OA'，通過兩次轉動，斜盤法向量的最終空間位置為OA'，兩次轉動可以等效為一次在ZOA'平面上的轉動，即法向量在ZOA'平面內由OZ轉動有效排量角δ到OA'，斜盤法向量的最終位置OA'在X-Y面上的投影即為死點軸，死點軸與配流盤對稱軸（X軸）的夾角即為錯配角ε，經過上述描述，將有效排量角δ、錯配角ε、交錯角α、排量角β放入到了四面體OAZA'中，下面通過數學推導得出有效排量角δ、錯配角ε與交錯角α、排量角β的函數關系。

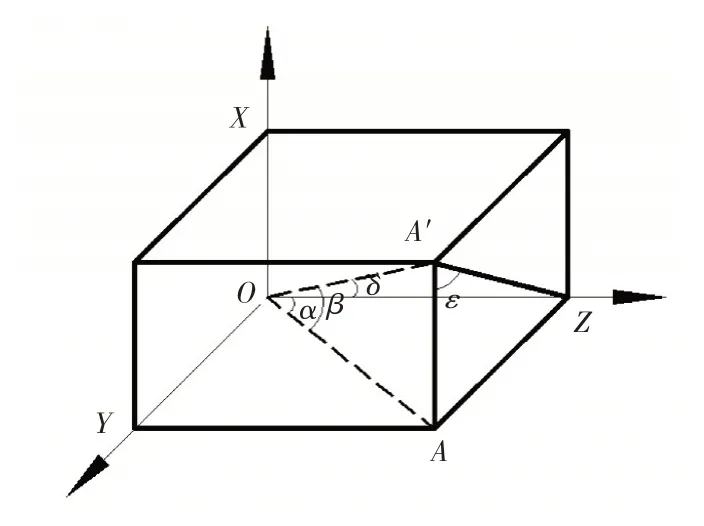
圖4 斜盤法向量轉動過程

1）δ與α、β的函數關系

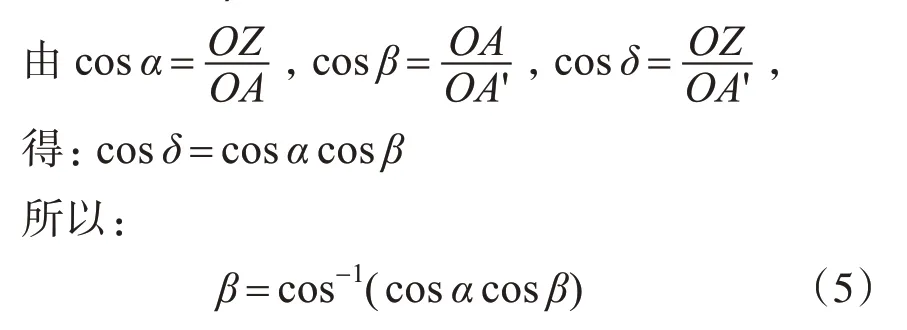
2）ε與α、β的函數關系

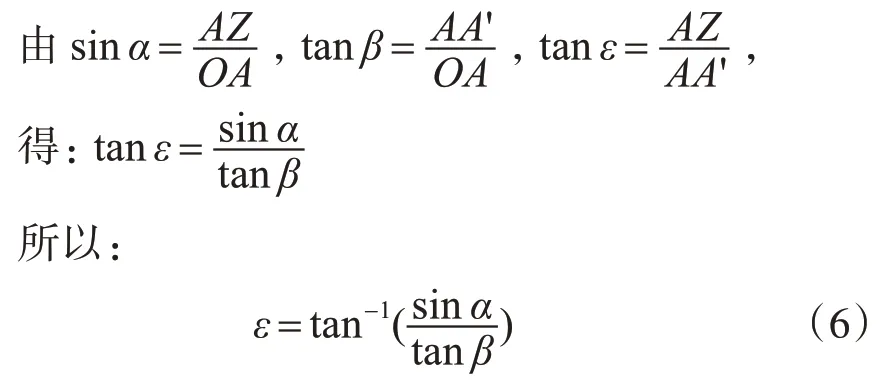
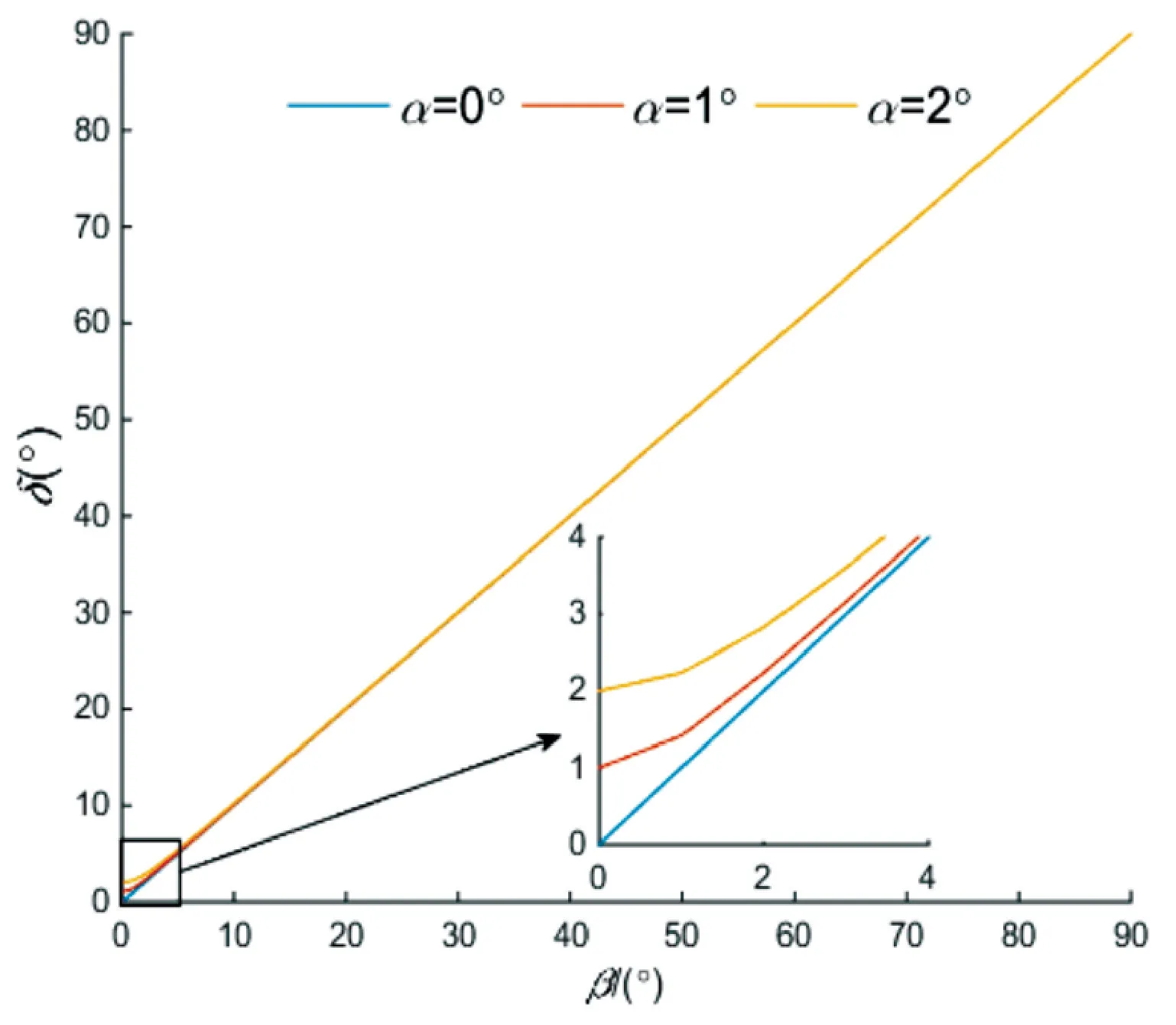
圖5 有效排量角δ 與α、β 的函數關系圖

斜盤的最大排量角通常在18°～20°之間［11］，所以圖5和圖6中的排量角β的范圍為0°～20°，本文采用的交錯角α范圍為-2°～2°［12］，由于對稱關系，圖5、圖6中的交錯角范圍為0°～2°。

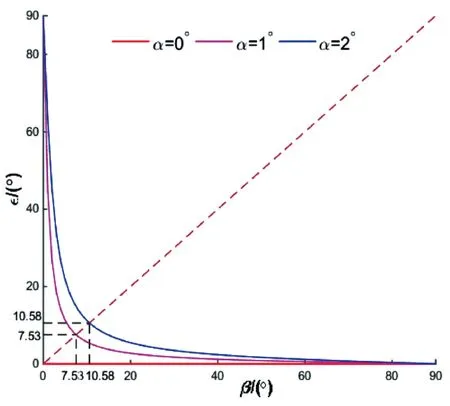
圖6 錯配角ε 與α、β 的函數關系圖

由圖5可知，斜盤的有效排量角受交錯角的影響較小，且與排量角近似相等。這是因為通常情況下交錯角較小，式（5）中的cosα近似等于1，將cosα≈1代入式（5）中得出δ≈β。所以在交錯角較小的情況下，柱塞泵的有效排量角近似等于排量角。

由圖6可知，斜盤的錯配角與排量角的關系曲線近似于雙曲線，該曲線相對于虛線ε=β對稱。當錯配角為1°/2°，曲線與虛線的交點為（7.53，7.53）/（10.58，10.58），當排量角由0°增加到7.53°/10.58°時，錯配角由90°迅速降低到7.53°/10.58°；當排量角由7.53°/10.58°增加到90°時，錯配角由7.53°/10.58°緩慢降低到0°。由此可見，隨著排量角從0°增加到90°，錯配角由90°下降到0°，且下降趨勢是先快后慢。

4 柱塞壓縮體積的數學分析

交錯角通過改變柱塞的運動規律影響柱塞在過渡區的壓縮體積和排油區的排量，過渡區的壓縮體積和排油區的排量都與柱塞的軸向移動距離成正比，兩者的區別在于包角大小不同［13］。如圖3所示，三角槽過渡區的包角?1為20°，而排油區的包角?2為180°，下面通過數學分析得出任意包角的柱塞壓縮體積的計算公式。柱塞的壓縮體積公式為

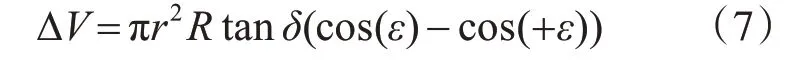
式中：r為柱塞半徑，mm；?為包角，°。

設ΔS=tanδ(cos(ε)-cos(?+ε))，則：

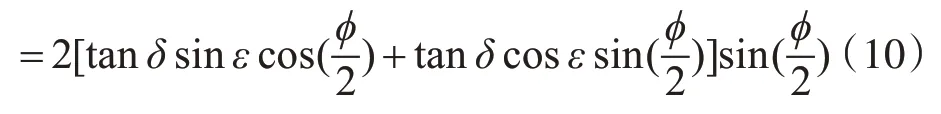
由圖4中的幾何關系可知：

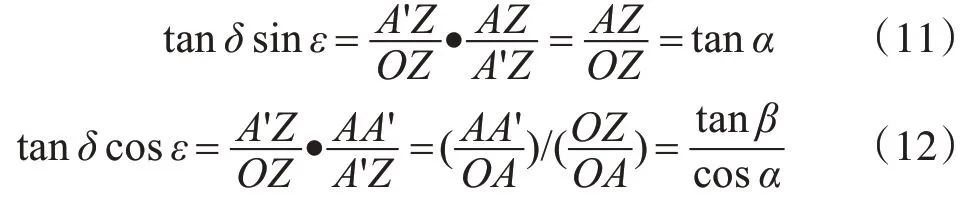
將式（11）、式（12）代入式（10）中，得：

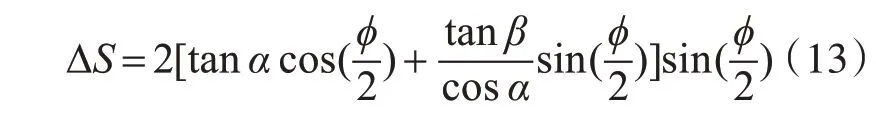
將式（13）代入到式（7）中，得：

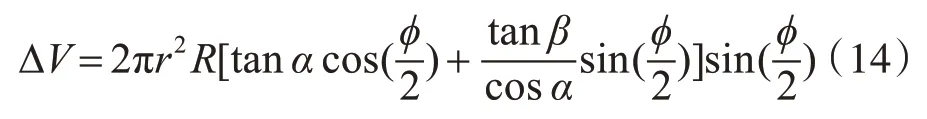
式（14）是計算任意包角大小的柱塞壓縮體積的一般公式，該公式中的自變量有三個，分別為交錯角α、排量角β、和包角?。如圖3所示，三角槽過渡區的包角?1=20°，排油區的包角?2=180°，將?1和?2代入式（14）中，則三角槽過渡區的壓縮體積為

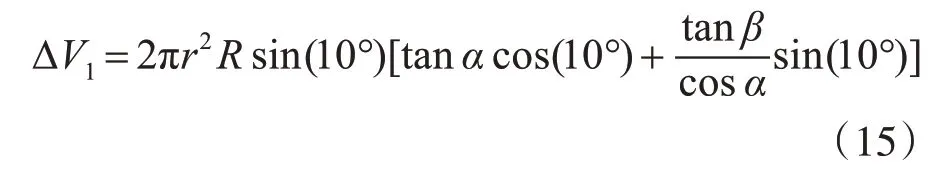
排油區壓縮體積（單柱塞排量）為

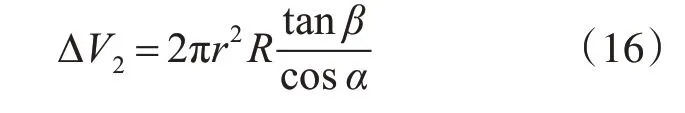
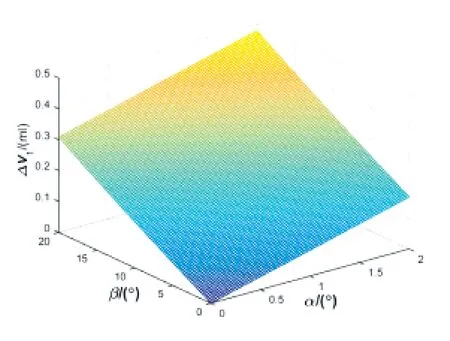
圖7 三角槽過渡區壓縮體積ΔV1與α、β 的關系

圖7和圖8是根據式（15）和式（16）得出的二維函數圖，圖中的排量角范圍為0°～20°，交錯角范圍為0°～2°，從圖8可以看出，交錯角對排量的影響微乎其微，排量的大小主要跟排量角有關。從圖7中可以看出，交錯角和排量角都對三角槽過渡區的壓縮體積有影響，圖7近似為一平面，表示交錯角和排量角可以近似線性改變過渡區的壓縮體積，由圖7可以看出，排量角每增加1°，壓縮體積增加0.015mL，交錯角每增加1°，壓縮體積增加0.084mL，相較而言，交錯角對于過渡區的壓縮體積的影響比排量角更加顯著。近似線性化后，三角槽過渡區的壓縮體積公式可簡化為

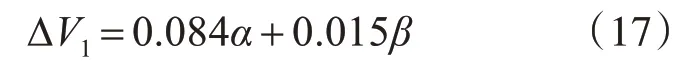
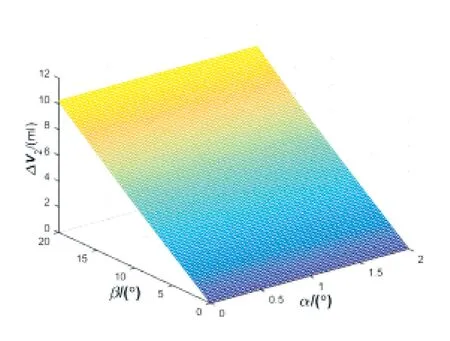
圖8 單柱塞排量ΔV2與α、β 的關系

5 單柱塞腔的仿真

單柱塞腔的流量特性對整泵有重要影響，如圖9所示，本文利用PumpLinx軟件建立了一個柱塞泵的單柱塞腔仿真模型，柱塞腔的仿真參數［14］如表1所示。

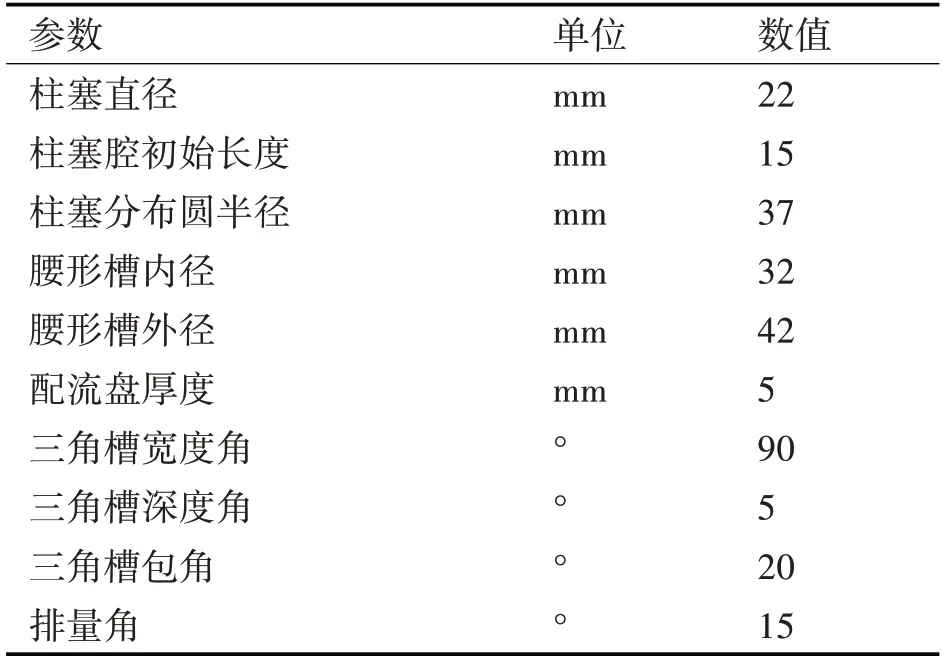
表1 仿真模型參數

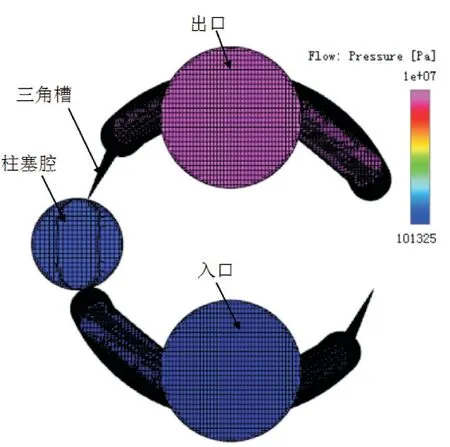
圖9 單柱塞腔的仿真模型

幾何流量：

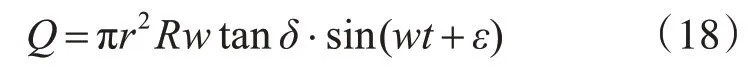
式（18）中的幾何流量Q為正弦函數，其中r表示柱塞腔的半徑，有效排量角δ與錯配角ε都可以由式（5）和式（6）計算得出，仿真模型的交錯角α范圍為-2°～2°，排量角β為一個固定角度15°，將交錯角α和排量角β的值代入到式（5）、式（6）中，得出不同交錯角下的有效排量角δ、錯配角ε，將α、β代入到式（17）中得到單柱塞腔在過渡區的壓縮體積。

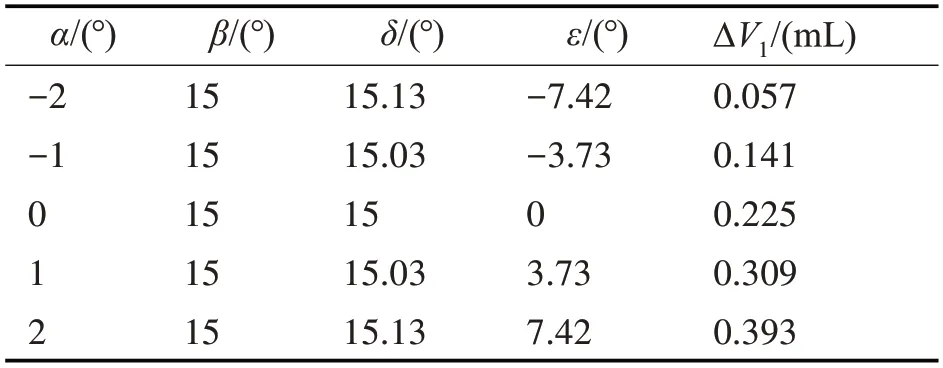
表2 交錯角與過渡區壓縮體積的關系

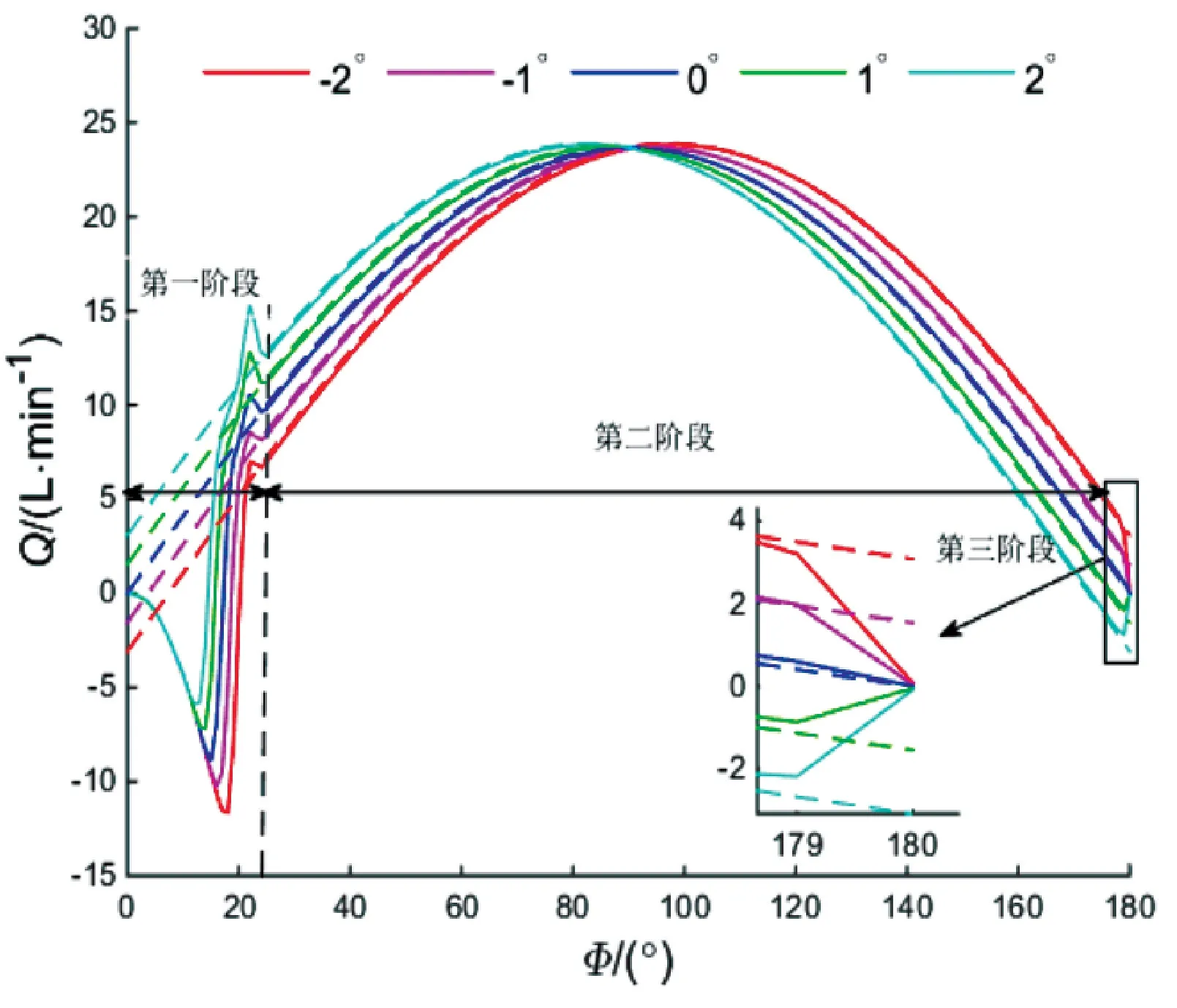
圖10 不同交錯角下單柱塞腔的幾何流量與仿真流量

圖11 不同交錯角下單柱塞腔內的壓力變化

圖10中的橫坐標Φ表示柱塞腔轉動的角度，虛線是根據表2中的δ和ε代入式（18）計算得出的幾何流量曲線，實線是通過PumpLinx仿真軟件計算得出的仿真流量曲線。

在第一階段，柱塞腔中的流體不僅受到倒灌流量的壓縮，也受到柱塞運動的壓縮，從表2中可以看出斜盤交錯角越大，柱塞在三角槽過渡區的壓縮體積越大，較大的壓縮體積有助于抑制流量倒灌現象，從而減小流量曲線的凹陷。此外，由于流體的慣性作用，柱塞腔中的流體被過度壓縮，又從柱塞腔反彈流回出口腰形槽中，形成一個波峰，從圖10中可以看出，斜盤的交錯角越大，波峰的幅值越大。

在第二階段，柱塞腔內的流體充分壓縮后不再反彈，在這一階段內，仿真流量與幾何流量重合，柱塞泵的流量脈動完全由幾何流量決定。

在第三階段，柱塞腔運動到與排油腰形槽的末端部分重合，兩者之間的流通面積急劇減小，流通阻尼極大，造成柱塞腔內近似處于封閉狀態。如果斜盤的交錯角為正，柱塞的負向速度會導致柱塞腔內的液體膨脹；如果斜盤的交錯角為負，柱塞的正向速度會導致柱塞腔內的液體被壓縮。

圖11是單柱塞腔仿真過程中的壓力變化情況，當柱塞處于第一階段，柱塞運動的壓縮作用和倒灌流量導致柱塞腔內的壓強急劇升高，造成壓力超調。從圖11中可以看出，斜盤交錯角越大，柱塞腔內的壓力超調量也越大，說明增大交錯角雖然能減小流量倒灌，但會增加壓力超調量。第二階段柱塞腔內的壓力平穩，幾乎沒有變化。第三階段，正的斜盤交錯角導致柱塞腔內的流體膨脹，負的斜盤交錯角導致柱塞腔內的流體壓縮。因此，正的交錯角可以讓柱塞腔內的壓力減小，有助于減小柱塞腔與入口的壓差。

6 整泵的工況分析

整泵的仿真模型如圖12所示，本文采用的是7柱塞泵，除柱塞數目外，整泵的仿真模型參數與單柱塞腔的仿真模型完全相同，本文將考察柱塞泵在不同轉速、壓力下的流量脈動率。

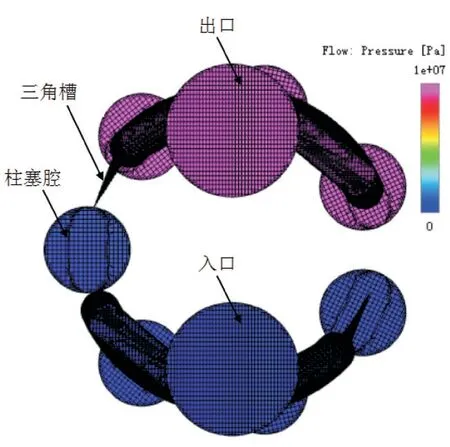
圖12 整泵的仿真模型

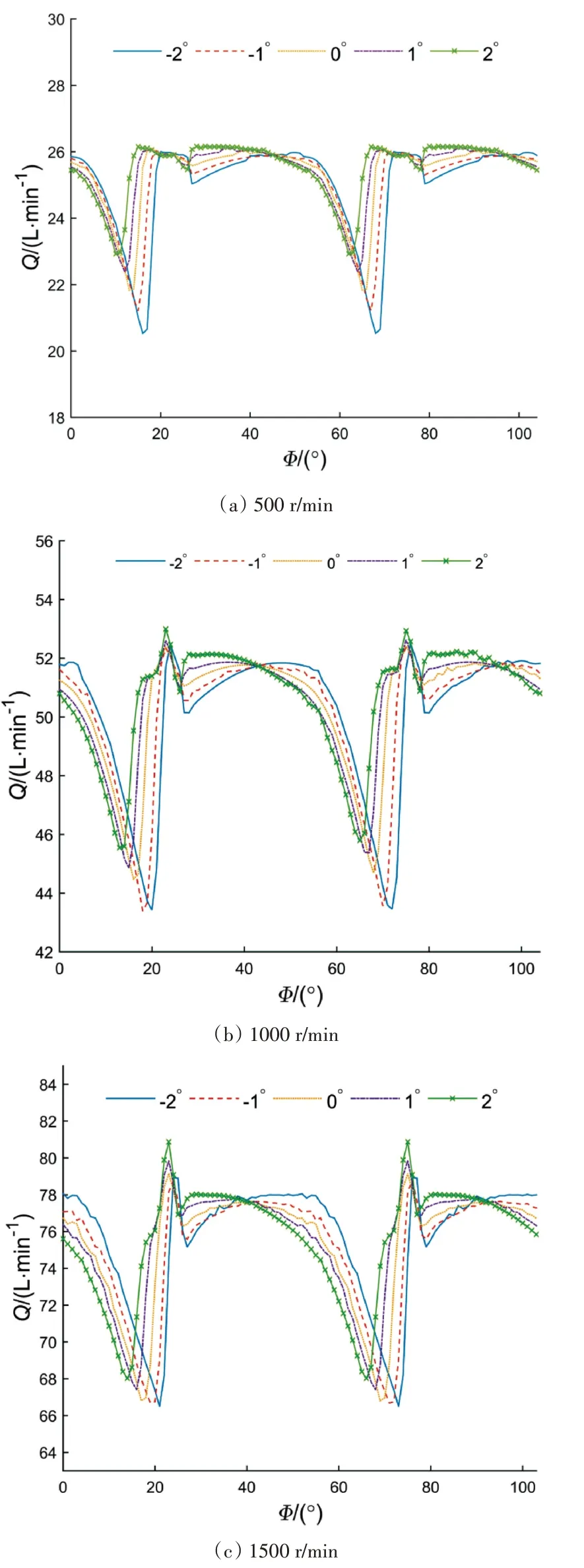
圖13 不同轉速下的出口流量

柱塞泵流量脈動率的計算公式［15］如下：

式中η表示流量脈動率，Qmax為波峰的平均值，Qmin為波谷的平均值。

根據圖13中的出口流量和式（19）得到不同轉速下的流量脈動率（表3）。從表3中可以看出，500r/min～1500r/min范圍內的脈動率均值隨著交錯角的增加而減小，當交錯角為2°時，脈動率均值最小。

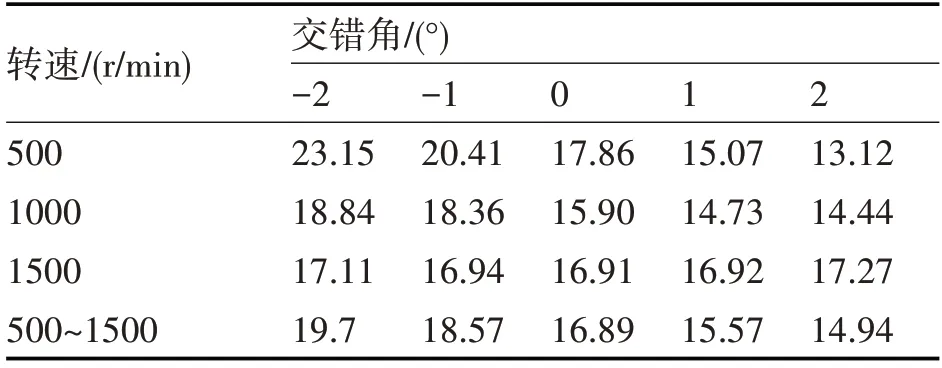
表3 不同轉速下的流量脈動率（%）

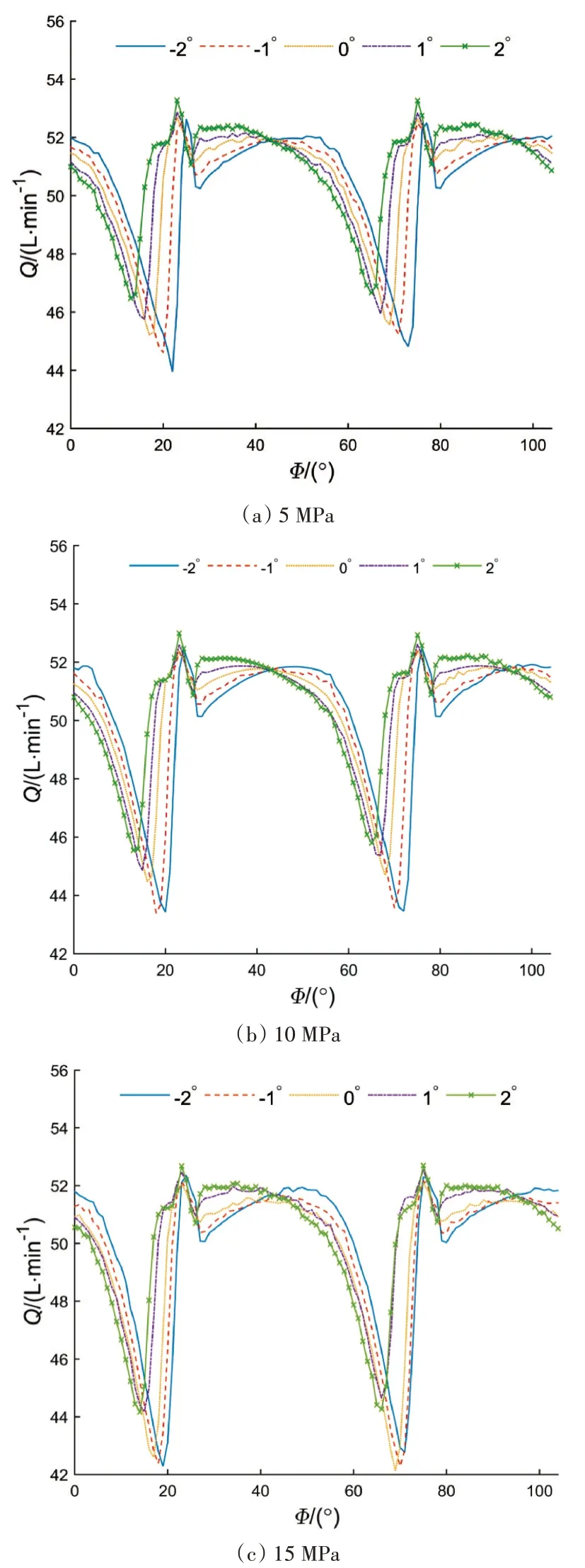
圖14 不同壓力下的出口流量

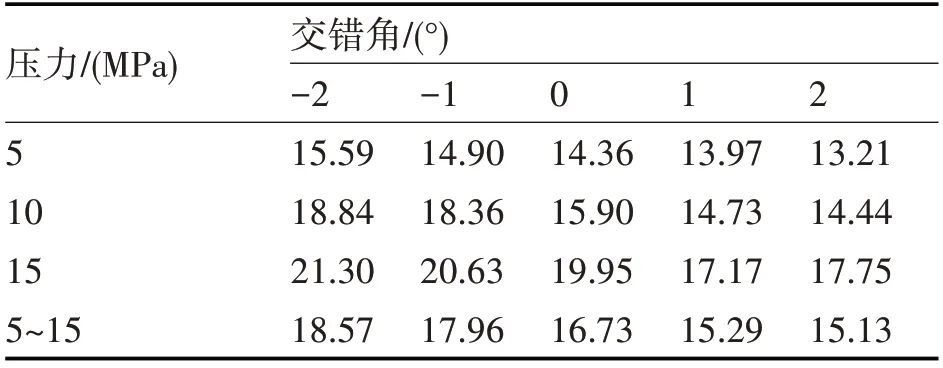
表4 不同壓力下的流量脈動率（%）

根據圖14中的出口流量和式（19）得到不同壓力下的流量脈動率（表4）。從表4中可以看出，5MPa～15MPa范圍內脈動率均值隨著交錯角的增加而減小，當交錯角為2°時，脈動率均值最小。

雖然無論是轉速還是壓力的脈動率均值都是交錯角為2°時最小，但都與交錯角為1°的脈動均值相差不大。如圖11所示，考慮到當交錯角為2°時，柱塞腔內的壓力超調量較大，所以取斜盤角錯角為1°是較為合適的設計。

7 結語

本文通過數學分析建立了交錯角與柱塞壓縮體積的函數關系。使用PumpLinx軟件仿真不同交錯角下單柱塞腔的壓力流量情況，和不同工況下的柱塞泵的出口流量，總結得出以下結論：

1）交錯角對三角槽過渡區的壓縮體積有重要影響，交錯角每增加1°，過渡區壓縮體積增加0.084mL。

2）增加交錯角可以減小單柱塞腔的倒灌流量，但會增加柱塞腔內的壓力。

3）綜合考慮柱塞泵的流量脈動率和壓力超調量，取柱塞泵的斜盤交錯角為1°是較為合適的設計。