凸極式無刷直流電機全速段復合矢量控制策略

張澤宇， 羅欣， 沈安文， 徐金榜

(華中科技大學 人工智能與自動化學院，武漢 430074)

0 引 言

與標準永磁同步電機(permanent magnet synchronous motor, PMSM)相比，非正弦氣隙磁密的無刷直流電機(brushless DC motor,BLDCM)具有制造成本低、功率密度和效率高等優勢，在工業領域得到了廣泛的應用[1-2]。其中凸極式無刷直流電機(interior permanent magnet type brushless DC motor,IPM-Type BLDCM)的轉子內置永磁體，機械結構堅固[2]，保證了電機在運行過程中可以獲得較強的穩定性和魯棒性。由于交直軸電感不對稱而產生了額外的磁阻轉矩，在需要較寬調速范圍及較大輸出轉矩的工業應用中優勢明顯。通過最大轉矩比 (maximum torque per ampere,MTPA) 控制可以充分利用磁阻轉矩，對定子電流矢量轉矩角進行控制以保證相同電流幅值情況下輸出最大電磁轉矩[3]。然而在運行過程BLDCM產生的轉矩脈動(尤其是換相轉矩脈動)在很大程度上限制了其在高精度場合的應用[4-5]。

常規的兩相饋電模式通過逆變器向電樞繞組中注入近似120°電角度平頂的方波電流，但由于電機中感性元件的存在和直流母線電壓的限制導致了開通相和關斷相的電流變化率難以預測，從而產生換相轉矩脈動[5-6]。文獻[7]通過控制正比于電機瞬時轉矩的合成電流來抑制轉矩脈動。文獻[8]中采用兩相/三相饋電的混合切換模式來改善直接轉矩控制下的電機性能。但是這些方法無法實現高低速區間及導通/換相周期間的控制策略統一，增加了算法的復雜性。此外對于凸極式電機，注入的方波電流難以消除由轉子凸極性引起的轉矩脈動分量。三相饋電模式可以靈活地控制逆變器的開管方式，從而能夠向繞組中注入具有諧波分量的定子電流來匹配不同電機的實際運行情況[9-12]，且該模式下電流的變化率要低于方波電流，可以更有效地利用直流母線電壓，也能避免控制算法在導通/換相周期的切換問題，從而有效控制轉矩。

由于閉環調節過程中的PI控制器本身具有帶寬限制，且對交流量跟蹤性能有限(尤其是在高速區)[13]，難以保證電流中的諧波分量可以注入到電機繞組中。文獻[14]利用磁滯控制器來注入電流，但因為開關頻率不固定導致其在大功率場合的應用存在局限。還有一類通過轉子定向引入各諧波分量的非同步旋轉坐標系來匹配電機反電動勢中的諧波分量[15-18]，包括使用傳統d-q軸的諧振控制器或重復控制器來拓展帶寬。這些控制器對頻率選擇較為敏感，因此在動態調節中易受干擾。文獻[19]中通過離線反電勢來構造隱極式電機的變換矩陣以使電流在新的坐標系下為恒定分量，并引入位置和幅度擾動來提高閉環響應。文獻[20]中提出了直接功率控制方案，但磁通估算涉及到的直流偏置及檢測誤差等問題會影響控制效果。文獻[9-10]提出了一種基于機電能量轉換的控制策略，既可以應用于凸極式電機，也適用于隱極式電機。

基于對同步電機的機電能量轉換原理進行分析，并結合轉子運動過程中的矢量關系，本文采用一種復合矢量控制策略來實現電機全速區間的MTPA軌跡跟蹤及轉矩控制。為了同時滿足電機調速范圍及轉矩控制的性能要求，當電機運行在中低速區間時使用近似MTPA模式，高速區則切換到實際MTPA模式，并通過適當的坐標變換提取出電流中的轉矩分量加以控制從而提高閉環動態響應。針對電機運行過程中參數易受溫升、負載突變等環境影響，且寄生耦合參數項也會影響轉矩控制，引入了一種簡化的等效辨識方案來快速準確地獲取實時參數。最后，通過實驗數據對本文所提方案加以驗證和分析。

1 凸極式無刷直流電機的數學模型及MTPA控制策略分析

由于無刷直流電機內部的氣隙磁密不是理想正弦型，導致其轉子磁鏈等折算到定子側d-q軸無法完全解耦，難以直接通過傳統的轉子磁場定向進行矢量控制。本文的電機數學模型需要結合靜止坐標系進行分析。

1.1 靜止坐標系下的電機模型及MTPA狀態轉矩角計算

三相同步電機的定子側電壓矢量可以表示為

us=uα+uβ=2(ua+ub+uc)/3。

其在α-β軸的方程為

(1)

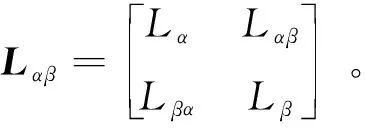
(2)

式中：e為電機反電勢矢量的幅值，eα、eβ為其在α-β軸分量；θemf為反電勢矢量與α軸的夾角，也即q軸和α軸的夾角，滿足θemf=θr+π/2，矢量關系如圖1所示。ec在靜止坐標系的分量可以表示為

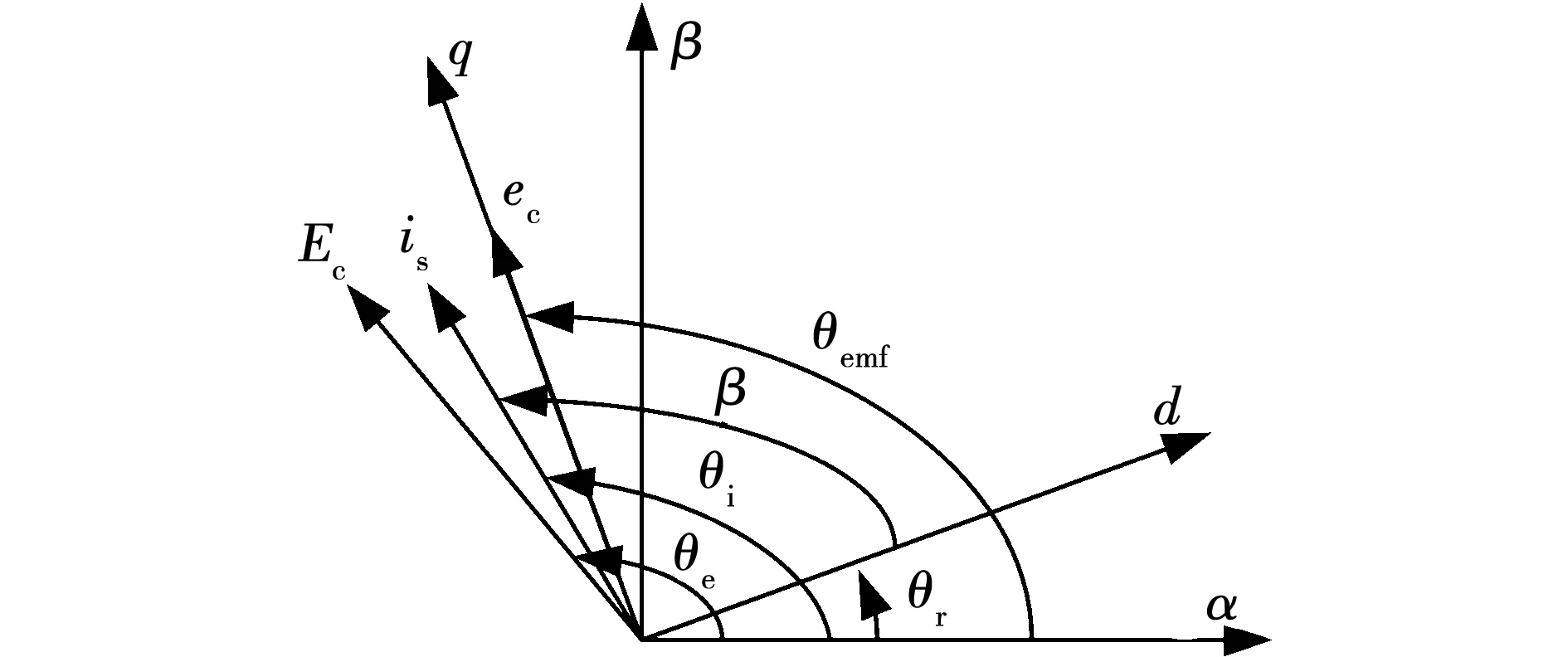
圖1 IPM-BLDCM坐標圖Fig.1 IPM-BLDCM coordinate diagram

ecα=eccosθemf=-ecsinθr,ecβ=

ecsinθemf=eccosθr。

(3)

根據電機統一理論及機電能量轉換關系[9-10]，電機運行過程中輸出的瞬時轉矩為：

(4)

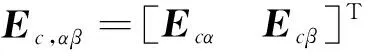
Ec,αβ=Le,αβ+ec,αβ。

(5)

式中Le在α-β軸的分量為：

(6)

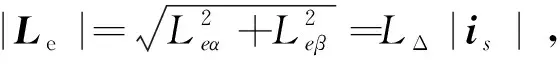
(A1+A2)|is|+|ec|cosβ=0。

(7)

式中：A1=sin2θiD(Lβ-Lα)/2,A2=cos2θiDLαβ；θi為電流矢量is與α軸的夾角；β=θi-θr為電流矢量的轉矩角，也即is與d軸的夾角。根據式(7)可得MTPA狀態下轉矩角的參考值為

(8)

式中LΔ-=(Lβ-Lα)/2cos2θr。

1.2 基于機電能量轉換原理的電機模型分析

理論上將式(4)中的Xe參考值置零可以消除無功損耗[9-10]，這種情況下瞬時電流矢量可以表示為

(9)

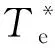
(10)

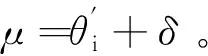
LΔ|is|cos2(ξ+δ)=eccos(ξ+δ)。

(11)

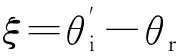
(12)

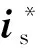
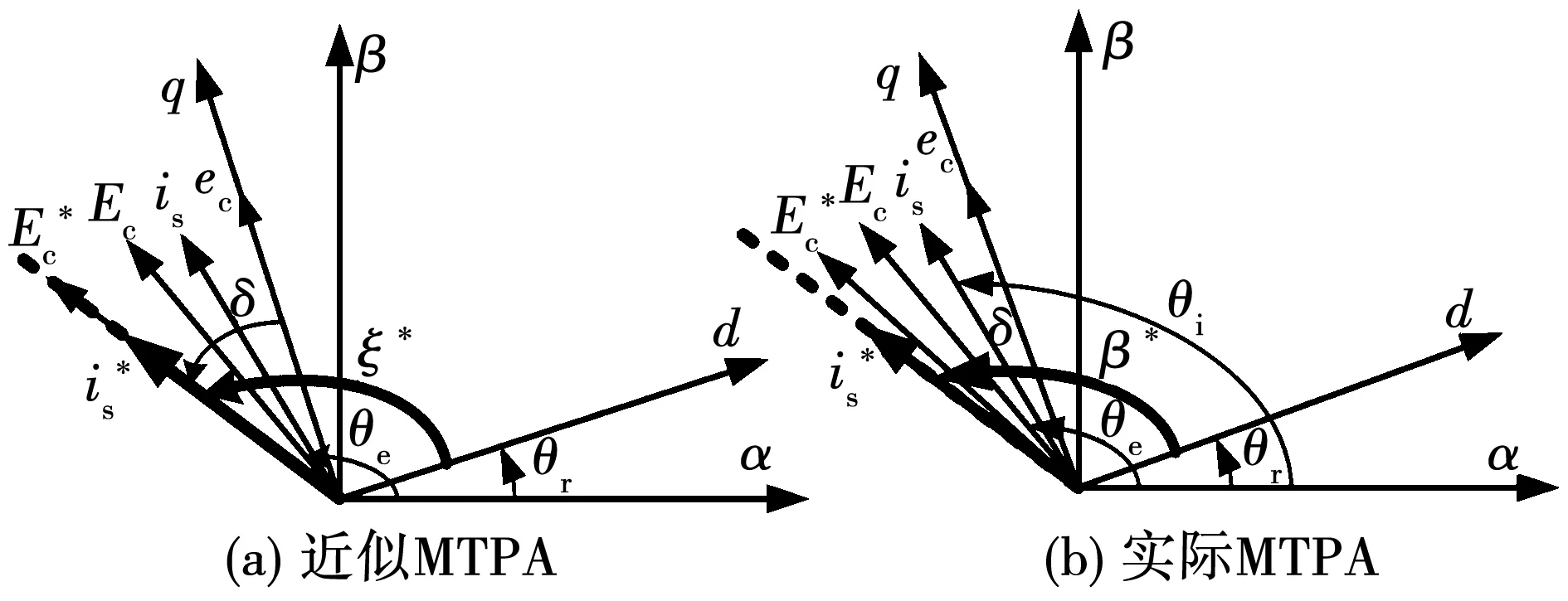
圖2 2種MTPA狀態下的矢量關系Fig.2 Vector relation of two MTPA states

由于Ec和is無法完全解耦，導致運行過程中其相位變化存在不確定性，因此，實際控制過程中理想的近似MTPA狀態是否存在需要驗證。如果Ec和is的相位永遠無法相同，或者在運行過程中計算出的轉矩角ξ*超出函數域有效范圍，則理想情況下的近似MTPA狀態便不存在。在1.3節中，將對近似MTPA狀態的存在性及有效性進行分析證明。

1.3 動態過程中的近似MTPA轉矩角存在性分析

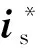
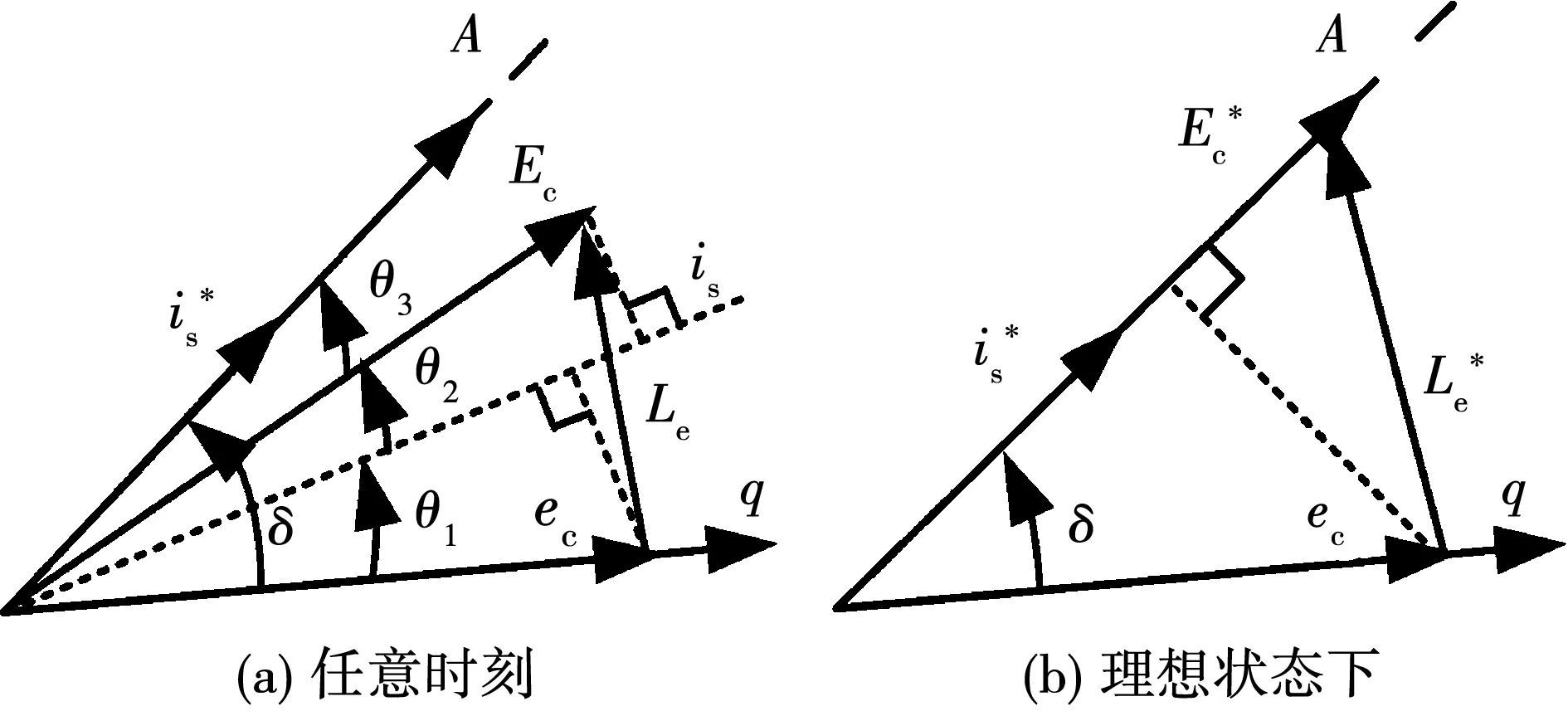
圖3 不同狀態下和能量轉換相關的矢量關系Fig.3 Relationship of vectors related to energy conversion in different states

圖3(a)中，is在Ec方向和q軸的投影分量分別為iE=iscosθ2、isq=iscosθ1。電機的電磁轉矩可以表示為

(13)

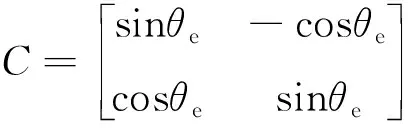
(14)

式中：iA為is在A軸方向的投影；γ=β*-ξ*。將常規轉矩方程與式(13)中計算得到的公式聯立可得

|Ec|cosθ2=[-2LΔisd+|ec|]cosθ1。

(15)

圖3(b)為理想近似MTPA狀態下的矢量關系示意圖，結合式(15)可知這種情況下滿足

|Ec|=[-2LΔisd+|ec|]cosδ。

(16)

(17)

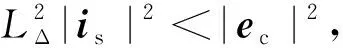
圖4為負載3 N·m和6 N·m時MTPA狀態的定子電流幅值，可以看出相同負載條件下2種狀態的電流幅值幾乎相等，這說明對應的β*和ξ*偏差較小。在工程應用中有時會出現短期的過載運行(一般小于3倍過載)，由于實際MTPA狀態下的|isd|更大，因此在高速重載運行時其轉矩控制效果更佳，調速范圍也更寬。

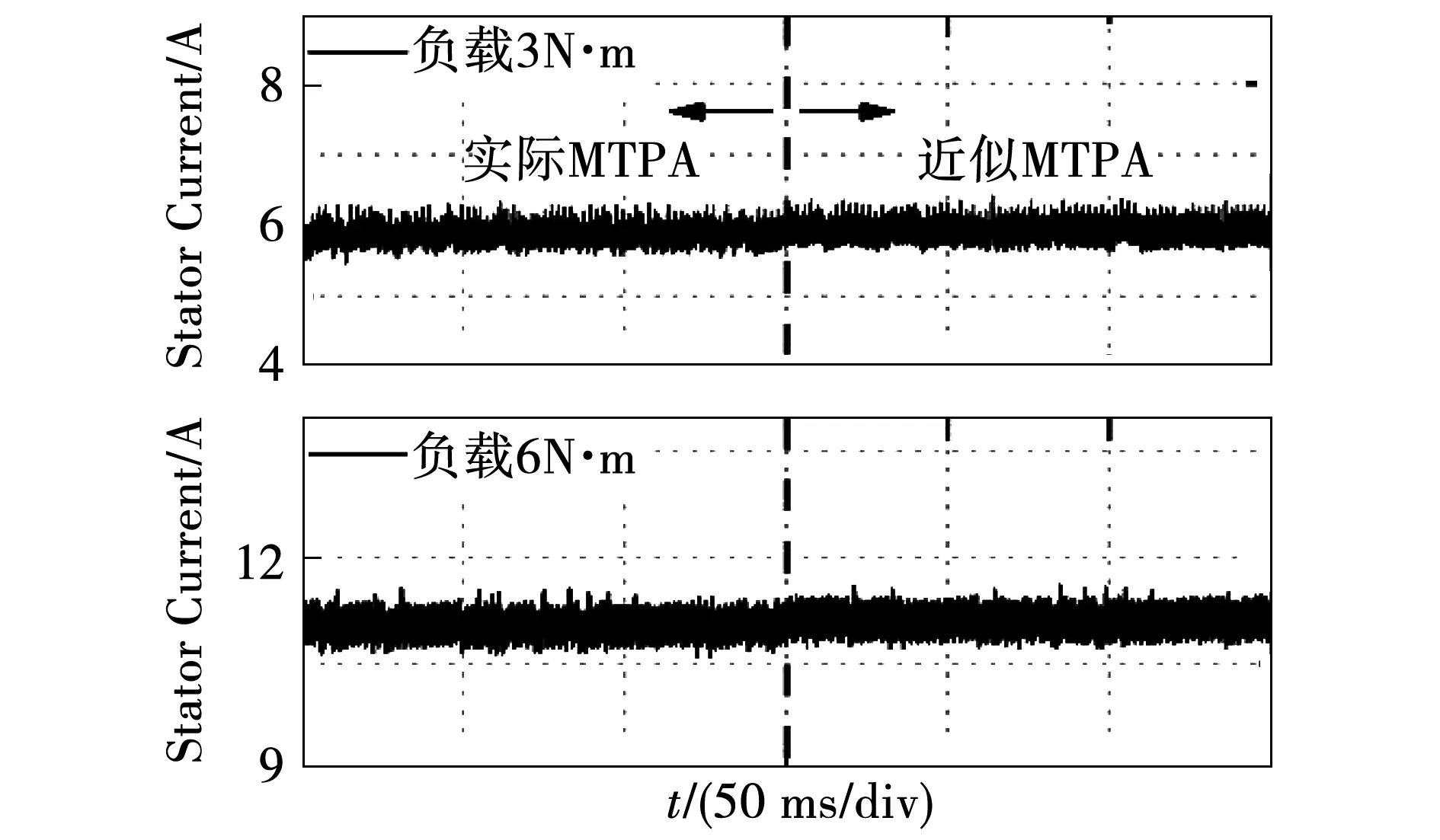
圖4 不同負載條件下近似和實際MTPA狀態的電流幅值Fig.4 Current amplitudes of approximate and real MTPA states under various load conditions

從式(14)中可以看出通過Ec或is定向的坐標變換，2種模式下的電機轉矩都可以和對應的電流相關，這樣就可以更為直接地進行轉矩控制。根據式(5)可知Ec主要包含LΔ和ec,αβ2組電機參數，以及理想狀態下的電流矢量，因此在電機運行過程中需要實時獲取這些參數。

2 可變電機參數的等效辨識方案

2.1 復雜電機參數對電磁轉矩控制的影響

常規模型中，實際MTPA狀態下的電機參數和電流，滿足如下關系[9,23-25]

(18)

式中：iT=isdMTPA/isqMTPA。isdMTPA和isqMTPA分別為電機運行在MTPA狀態下的d-q軸最優電流分量;M=|ec|/2LΔ為電機組合參數項。考慮到凸極式電機驅動過程中isd/isq<0，為了使電機狀態方程更直觀，重新定義iT=-isdMTPA/isqMTPA,則MTPA狀態下的轉矩方程[24]為

(19)

如果瞬時值|ec|已知，以iT為自變量，則轉矩Te和iT滿足正相關關系，且該方程具有奇函數性質。這意味著在閉環控制中iT的大小可以反映負載轉矩的實際變化情況，也即速度外環的PI輸出與iT具有對應關系。一旦獲取到實時M和iT的數值，那么對應的最優電流幅值及相位關系也可以同時計算出，反之亦然。該等效關系可以避免計算中存在式(8)和式(12)的開方等復雜運算。實際電機運行過程中由于|ec|會隨著轉子位置的變化而變化，因此對于凸極式無刷直流電機而言，其在穩定MTPA狀態下的電流轉矩角并非理想固定，而是會出現周期性波動，電流值也會存在波動。此外，不同結構的電機在控制效果上也會存在差異。

考慮交叉耦合效應和定子電流對電機參數(不對稱電感項及轉子磁鏈項)的影響，文獻[23]對電機在MTPA狀態下的約束條件進行了分析。電機運行過程中MTPA電流軌跡不僅取決于常規參數，而且也受寄生耦合項及參數相對于電流的偏導項的影響。單獨對每個電機參數進行辨識計算的過程較為繁瑣，需要通過實際的預測量實驗來獲取部分精確數值進行記錄，作為后續電機運行過程中通過等效關系快速辨識其他數值的依據。

2.2 簡化的電機參數等效辨識方案

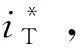
(20)

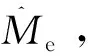
由于具有對外部擾動不敏感，以及動態性能好等優勢，滑模觀測器廣泛應用于電機控制[21-22]。因其參數魯棒性較強，對凸極性較低的電機而言，隱極式電機的滑模狀態方程可以沿用,但不適用于凸極性較高的電機。結合式(1)～式(3)及凸極式電機擴展反電勢的計算方案[21]可得

(21)

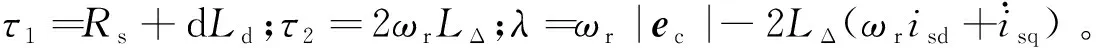
(22)

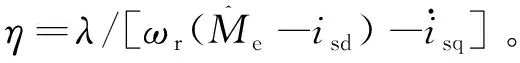
對于反電勢平頂部分較大的電機或對控制精度要求嚴格的場合，也可以通過預測量實驗來直接獲取|ec|數值并存儲在芯片中，但是要考慮溫度對永磁體磁鏈的影響[18]。盡管隨溫升等變化永磁體磁鏈會變化，將導致|ec|值跟著改變而產生控制偏差，不過在工程應用中是可以接受的[9]。

圖4結果表明，2種MTPA模式下的電流幅值偏差很小，為了簡化式(8)和式(12)中的計算，可以將等效辨識獲得的Ec用于近似MTPA模式下的坐標運算。圖5所示為簡化的電機可變參數等效辨識方案，可以快速獲取數值并降低運行過程中復雜參數及環境因素對于運動控制精度的影響，避免了對離線參數的過度依賴而導致無法與受溫升、磁路飽和等影響而變化的實際參數相匹配的弊端。經過等效辨識方案獲得的參數可直接應用于電機的復合矢量控制方案。

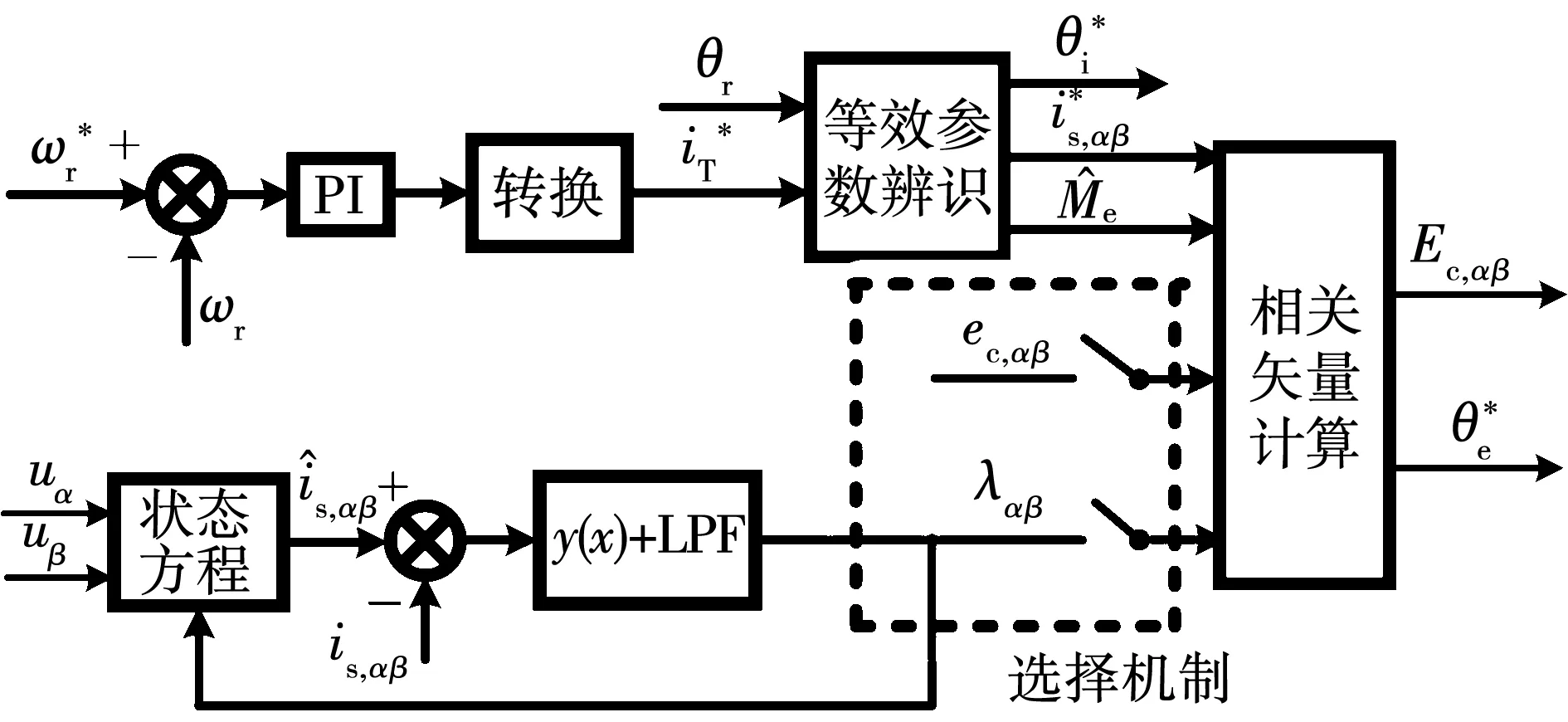
圖5 簡化的電機可變參數等效辨識機制Fig.5 A simplified equivalent identification scheme for motor variable parameters

3 最優分配的復合矢量控制方案

通過等效辨識方案獲取相關參數之后，需要通過全速范圍調節的復合矢量控制方案來有效控制電機。式(14)中近似MTPA模式下的轉矩方程中的交流量較少也較為直觀，這意味著在閉環控制中可以獲得更高的控制精度及響應速度。結合前面的分析，當電機運行在中低速區或輕載條件下時通過近似MTPA模式控制，可以保證在簡化計算及提高閉環動態響應的同時輸出較高的電磁轉矩并實現換相轉矩脈動抑制；在高速區或應用場合對電機轉矩轉速要求較高時切換到實際MTPA模式進行控制，計算步驟會增加，但是可以保證電機運行在更寬的調速范圍和輸出轉矩范圍。

中低速區運行在近似MTPA模式，從式(14)中可以看出電機轉矩公式中包含隨轉子位置變化的交流量|Ec|，因此對于給定的輸出轉矩，iA并不是一個常量，這也會導致閉環控制中電流跟蹤性能的下降，且對轉矩控制產生影響。所以變換矩陣中需要將交流量|Ec|也考慮在內，這樣經過變換后在新的坐標系下就可以對和轉矩直接相關的電流進行控制[9]。簡化后的坐標變換矩陣及其逆矩陣分別為

(23)

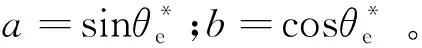
高速區則切換到實際MTPA模式，結合上述分析，該模式下對應的改進型變換矩陣及其逆矩陣為

(24)

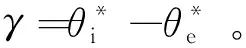
圖6所示為電機復合矢量控制方案框圖，以保證在不同速度段及負載條件下匹配到合適的控制方案。通過引入等效辨識策略，近似和實際MTPA模式都可以通過部分實測的數據來重構電機運行過程中的完整參數曲線，避免了單純依賴初始離線參數的數學計算所帶來的誤差，從而實現了考慮不確定性因素在內的凸極式電機寬轉速轉矩范圍的矢量控制。

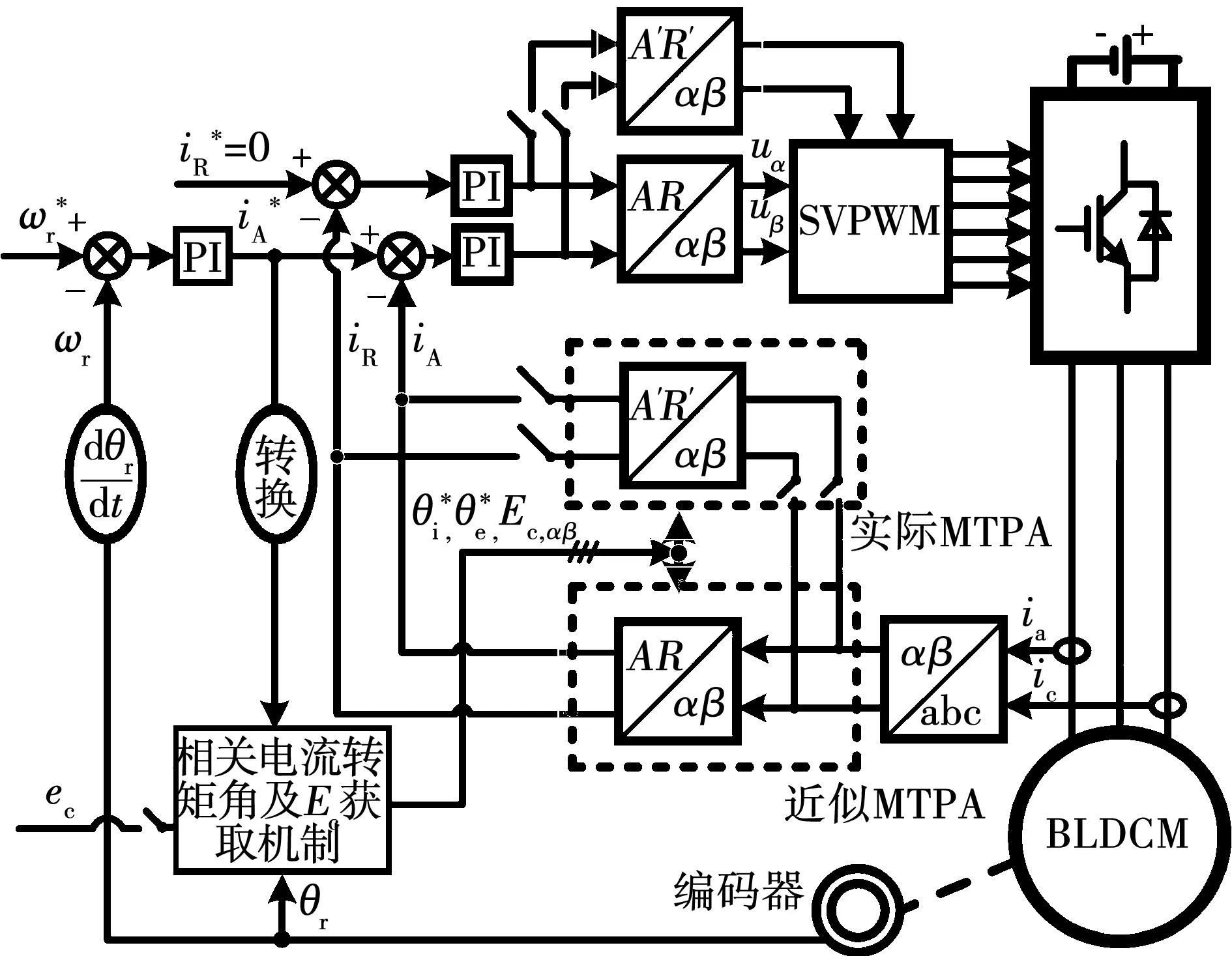
圖6 復合矢量控制方案框圖Fig.6 Block diagram of the compound vector control scheme

4 實驗分析

用于測試本文所提策略的實驗裝置如圖7中所示。微處理器采用主頻為72 MHz的ST芯片，控制頻率為16 KHz。實驗結果由PC上位機及數字示波器記錄，負載由對拖PMSM提供。為了對控制方案進行驗證，實驗將從穩態和動態性能2個方面入手，對采用常規矢量控制方案(下簡稱比較方案1)、基于GSRF的矢量控制方案[9-10](下簡稱比較方案2)以及本文所提方案進行對比試驗分析。實驗電機參數如表1所示。

圖7 實驗裝置圖Fig.7 Experimental setup

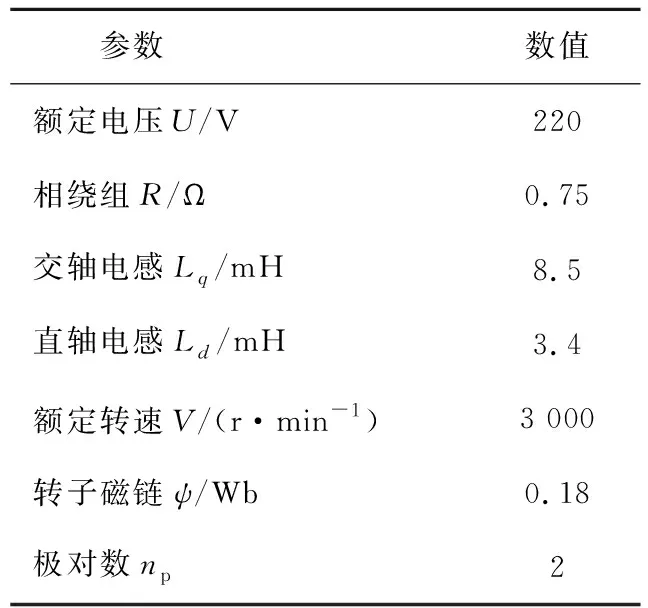
表1 電機參數Table 1 Parameters of motor

4.1 矢量控制方案的穩態性能分析

實驗中分別將電機的給定轉速和轉矩設定為1 000/3 000 r/min及2/7 N·m，不同控制方案對應的定子電流幅值及電磁轉矩波形如圖8所示。可以看出在不同轉速區間的相同負載條件下，本文所提方案的定子電流幅值低于另外2種方案，這說明在相同定子電流幅值情況下可以輸出最大的電磁轉矩。從圖中的穩態轉矩波形也可以看出復合矢量控制方案的電磁轉矩脈動要小于另外2種，這表明通過適當的坐標變換后可以提取出電機定子電流中的轉矩分量，并通過閉環矢量控制有效抑制凸極式電機的換相轉矩脈動。需要說明的是文獻[9-10]都是基于GSRF(generalied synchronous reference frame)來進行電機矢量控制，文獻[9]中改進的GSRF矢量控制策略，在動態響應特性及轉矩控制精度等方面明顯優于文獻[10]中的方案，但由于未考慮電流和機電能量轉換矢量之間的耦合性，因此單純依靠采樣瞬時電流值進行變換矩陣的計算會存在偏差，無法定位到給定負載下的最小電流參考值。

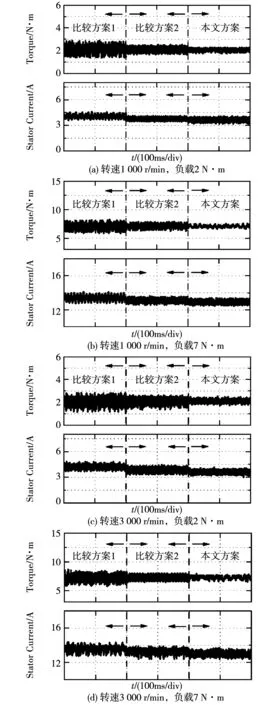
圖8 不同轉速及負載條件下3種矢量控制方案的定子電流幅值及電磁轉矩波形Fig.8 Stator current amplitudes and torque waveforms of three control schemes under different speeds and loads

4.2 矢量控制方案的動態性能分析

為了驗證所提方案的動態性能，首先通過3-7-3 N·m的階躍負載突變實驗進行測試，將比較方案2[10]及本文所提方案在相同工作環境下進行實驗，電流響應結果如圖9中所示。圖中箭頭所指即為不同負載條件下的MTPA電流值。從圖9(b)可以看出，在階躍負載擾動過程中，系統可以從初始MTPA狀態調整到與突變負載對應的MTPA狀態，且調整后系統狀態平穩。因此，所提方案顯示出良好的動態性能和對外界擾動較強的魯棒性。與所提方案相比，基于GSRF的控制方案[10]的電流與理想MTPA狀態的電流存在偏差，如圖9(a)所示。

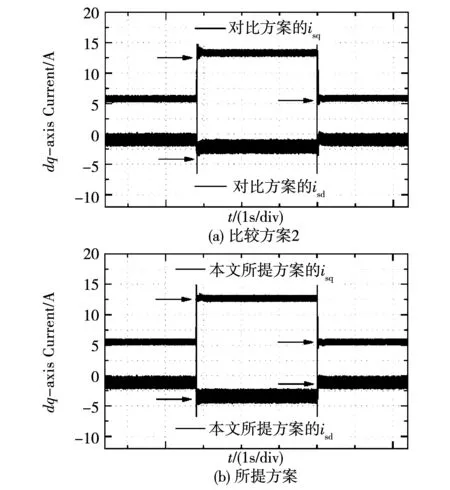
圖9 不同方案在階躍負載擾動為3-7-3 N·m時的電流響應Fig.9 Current response results of different schemes with step load disturbance 3-7-3 N·m

當給定轉矩突變時，如圖10所示，所提方案的輸出轉矩可以快速跟蹤其給定值，這是因為該方案可以將電機電流中的轉矩分量直接提取出來并加以控制，因此實現了輸出轉矩的快速響應。圖11所示為所提方案通過逆變器注入到電機繞組中的三相電流波形。與兩相饋電方波電流不同，該方案可以根據電機實際情況注入含有一定諧波分量的近似正弦相電流以實現轉矩控制，從而將抑制轉矩脈動的有效諧波分量注入到電機中。因此，所提方案增強了電機轉矩的穩態控制性能及動態響應特性。

圖10 不同方案在階躍負載為3～6 N·m的轉矩響應Fig.10 Torque waveforms of various schemes with step reference torque from 3 to 6 N·m

圖11 所提方案的三相電流波形Fig.11 Three-phase currents waveforms of the test motor with the proposed scheme

5 結 論

本文基于機電能量轉換理論及運動控制中的矢量分析，并通過簡化的可變參數等效辨識機制來實時獲取電機運行過程中的實時參數，提出了一種可以實現電機的MTPA軌跡追蹤及換相轉矩脈動抑制的全速段復合矢量控制策略。該策略在減少運算量的同時避免了傳統電機離線參數建模時難以考慮復雜參數項的問題，提升了電機的控制精度。為有效控制電機轉矩并提高閉環動態響應，同時滿足電機較寬調速范圍的性能要求，當電機運行在中低速區間時通過近似MTPA模式來簡化計算并實現較大電磁轉矩輸出，在高速區則切換到實際MTPA模式以進行高轉速轉矩的運動控制。實驗證明通過合適的坐標變換可以將電機定子電流中的轉矩分量直接提取出來，從而達到像常規永磁同步電機矢量控制那樣實用性強的效果。將不對稱電感產生的磁阻轉矩項置零，則該控制方案同樣適用于隱極式同步電機的最大輸出轉矩控制。