制動夾鉗單元靜強度驗證與確認

趙金良 孟永帥 劉 超

(中車戚墅堰機車車輛工藝研究所有限公司 江蘇 常州 213011)

有限元仿真分析技術正在不斷快速發展，廣泛應用于實際工程的設計當中。例如在汽車、船舶、飛行器、甚至是在日常使用的消費品當中[1]。因其具有建模時間短、成本低、能夠縮短研發時間的優點，有限元分析在機械產品設計過程當中的作用越來越重要。但是，不同的有限元建模方案會導致不同的有限元仿真結果，而結果的準確性直接代表了有限元仿真建模方案的可行性。因此有限元仿真結果的準確性是工程設計和分析人員以及決策者最為關心的問題。如何評估與確定仿真結果的準確性成為仿真工作最為重要的環節之一。

ASME V&V是針對無全系統試驗結果時的數值模擬準確性進行的嚴格量化的研究[2]，其目標就是對模型的仿真與試驗的準確性進行驗證與確認，使其模型的準確性有足夠的理論依據和保證。

本文以某型號制動夾鉗單元的靜強度分析為研究對象，基于ASME V&V標準，確定該型號制動夾鉗單元有限元模型的驗證與確認方案，并評估該模型有限元仿真結果的準確性。

1 ASME V&V標準

ASME V&V標準是由美國機械工程協會(The American National Standards)制定。其標準主要包含兩個部分：驗證(Verification)和確認(Validation)；驗證是評估計算模型是否精確地反映了數學模型的過程，確認是從模型使用程度的角度評估了模型是否精確反映了真實情況的過程[3]。

ASME V&V需要給出一種置信度，這個置信度是用來解決復雜問題的從計算得到的結果。但是，與其他標準不同，V&V標準并沒有給出確定的每個步驟的具體操作規則，而是給出了一種處理問題的觀念和想法，它是靈活的[3]。因此，對于驗證與確認的方法，要研究適合該型號制動夾鉗的確切方案。

2 驗證與確認方案

2.1 驗證方案[4]

ASME V&V給出了一套參考的評價方法，因為ASME V&V有限元驗證方案只適用于受拉伸載荷的情況，對于受彎矩或者扭矩載荷的情況，并不具備驗證能力。因此，本文選用J.R.Beisheim給出的驗證方案[4]，具體如下：

利用公式

hm=hm-1/λ

Nm=λ3Nm-1

其中：公式中需滿足m≥2；hm為變量m的網格尺寸，Nm為變量m的網格中的有限元單元數，λ為有限元細化比例常數。

而對于一個特定物體，通過有限元應力計算結果，得到相應的應力誤差，從而評估有限元網格的誤差：

Δσm=σm-σm-1

em=σ-σm

其中：σ為真實應力值，σm為變量m的應力值，em為應力值誤差，εm為有限元驗證因子。

因為真實應力值σ很難得到，因此通過有限元迭代法去估計真實應力值的大小，并應用以下公式：

最終百分比誤差計算公式為：

評估其是否符合標準要求。

2.2 確認方案[5]

確認方案采用了ASME V&V給出的確認評價方案。

其原理是通過建立模型與試驗的分布函數的積分，計算出因誤差而導致的積分差面積，通過其面積指標給出仿真與試驗確認的準確性指標。其積分函數如圖1所示。

圖1 分布函數及面積指標

仿真模型的正態分布概率積分為

試驗數據的正態分布概率積分為

根據上述兩個式子得到面積指標為：

其中，Sexp為試驗采集數據的平均值。

其面積指標標準要求需要小于10%。

3 制動夾鉗單元建模與驗證

分析某型制動夾鉗單元的結構特點，并根據其結構特性，利用商業有限元軟件建模。

3.1 制動夾鉗單元結構

制動夾鉗單元的結構如圖2所示。制動夾鉗單元的工作原理是利用杠桿原理把制動缸的推力轉化為前端閘片托的夾緊力。

圖2 某型制動夾鉗單元結構示意圖

3.2 制動夾鉗單元有限元模型

制動夾鉗單元的有限元模型如圖3所示。

圖3 制動夾鉗單元有限元模型

分別將制動夾鉗單元的材料屬性、加載載荷、邊界條件輸入到有限元軟件當中。其加載載荷與邊界條件需要與其確認試驗相對應。

在有限元模型驗證與確認之前，需要對制動夾鉗單元系統進行分層。本文采用傳統分層方案，即：“系統→子系統→部組件(基準)→單元”的分層方案。其具體分層方案如圖4所示。根據其分層方案，制動夾鉗單元有限元模型的驗證與確認分析過程從杠桿構件開始。

圖4 制動夾鉗單元重要構件分層結構

3.3 制動夾鉗有限元模型驗證

驗證左邊杠桿模型。確定其驗證點位置，其驗證點的位置如圖5所示。再把校核點不同網格尺寸下的應力值帶入驗證方案并判斷其有限元模型是否符合標準。

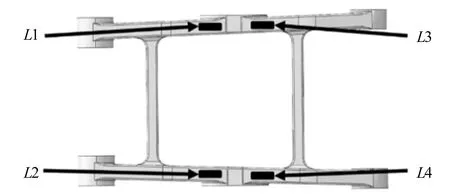
圖5 左側杠桿測點布置圖

對于L1測點：載荷工況下，不同網格大小的L1測點的應力值如表1所示。

表1 在載荷工況下不同網格大小的L1測點應力值

結合上述驗證方案可得

Δσ3=σ3-σ2=0.205 8

Δσ2=σ2-σ1=0.474 9

因此，在載荷工況下，測點L1周圍網格為1.8 mm時符合驗證方案的要求。

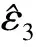
4 制動夾鉗單元模型確認

4.1 制動夾鉗單元確認試驗

確認試驗的原理是根據電阻應變測量技術使用電阻應變片測量測點應力值大小。需要注意的是確認試驗的實際載荷工況與邊界條件需要與有限元仿真計算時的載荷工況與邊界條件一致，并且應變片的測點位置需要與有限元網格測點位置相一致。靜強度試驗現場如圖6所示。

圖6 制動夾鉗單元靜強度試驗現場

為了確保試驗數據的準確性，盡量排除隨機誤差的干擾，試驗數據至少為100組，并整理出每個測點應變片的平均應力值與方差。整理好數據后與有限元模型的應力值進行確認對比。

4.2 制動夾鉗有限元模型確認

制動夾鉗有限元模型確認分析過程同樣需要根據其分層方案，先確認每個構件之后再確認整個制動夾鉗單元模型是否滿足要求。

首先，確認左邊杠桿模型，需要確認的測點如圖5所示。先從L1測點開始，在載荷工況下的確認試驗的平均應力測量值為21.4 MPa，方差為0.113。

結合上述的確認方案，可得：

MSRQ=0.06<0.1

因此，在載荷工況下，測點L1周圍網格尺寸為1.8 mm時符合確認方案的要求。

同樣的方法測得L2、L3、L4的MSRQ分別為0.110、0.048、0.076。測量結果表明：在網格大小為1.8 mm時，L1～L4共4個測點均符合確認方案要求。因此判定左側杠桿計算模型滿足仿真結果的準確性要求。利用同樣的方法也可以判定其他構件仿真模型滿足準確性要求。

5 總結

(1)對某型制動夾鉗單元建模，并依據ASME V&V標準對計算模型進行驗證與確認工作，最終確定其有限元分析模型的準確性滿足標準要求。

(2)ASME V&V的靈活性的特點使得其普適性很強。因此能夠廣泛應用于軌道交通機械設備，可以評價整個軌道交通系統模型的準確性。

(3)對于制動夾鉗單元模型，在能夠確定模型準確性滿足標準要求之前，對模型做出很多改動。其改動方向是：模型的加載載荷與邊界條件盡可能靠近確認試驗的加載載荷與邊界條件。通過不斷嘗試，得到滿足要求的制動夾鉗仿真模型。

(4)本文所使用的有限元驗證方案適用于多軸拉伸、扭矩和彎矩的載荷條件下的有限元模型。至于更復雜的有限元模型，該驗證方案的適用性仍需要進一步研究。

(5)本文所使用的有限元確認方案不僅考慮到了試驗數據的準確性，同時也考慮到了試驗數據的波動性，因此較為客觀、準確。

通過該型號制動夾鉗單元有限元模型滿足驗證與確認流程條件分析過程，可以得出結論：該型號制動夾鉗單元靜強度有限元模型具有一定的準確性，可以直接通過有限元模型來確定其應力分布。進而可以把滿足標準的建模方案推廣到相類似的制動夾鉗單元中，進而能夠大大縮短其他類似制動夾鉗單元研發與建模的時間。