一種基于改進的LMS算法光纖信道自適應均衡器的研究*

王敬輝 孫守梅

1.天津現代職業技術學院智能工程學院 天津 300350；2.天津職業技術師范大學電子工程學院 天津 300222

引言

色散導致光纖中的光信號在傳輸過程中產生失真，并且這種失真會隨著傳輸距離的增加越來越嚴重。其中多模色散、波導色散、材料色散和偏振模色散（PMD）是引起失真的主要原因。對數字光纖系統而言，色散造成光脈沖展寬導致前后脈沖相互重疊，引起數字信號的碼間干擾（ISI），造成誤碼率增大。隨著光纖通信系統傳輸速率的不斷提高，色散成為制約高速光纖通信系統發展的主要因素。因此，對高速率、長距離的光纖通信系統必須考慮色散補償問題，以消除ISI。

1 單模光纖信道的仿真模型

在理想信道中，發送濾波器和接收濾波器聯合設計成在所需求的采樣瞬時具有零ISI。即：

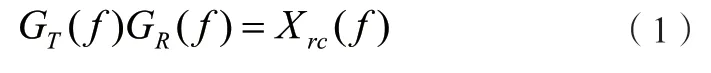
其中GT(f)為發送濾波器的頻率響應，GR(f)為接收濾波器的頻率響應，并且GR(f)為GT(f)的匹配濾波器，是升余弦頻率響應特性，那么在采樣時刻，ISI是零。然而，由于噪聲和色散對實際的光纖信道產生影響，它并不是理想的。

即信道產生了失真，其中G(f)F為實際光纖信道傳輸函數。為了消除光纖色散引起的碼間干擾，我們在接收端加一個自適應均衡器GE(f)，并且使：

系統仿真模型如圖1所示，待發送數據經發送濾波器后進入光纖信道，再經采樣后進入自適應均衡器，均衡器輸出信號進入判決器，判決后輸出，期望信號d(n)和均衡器輸出信號) 進行比較，得到誤差信號，以LMS自適應算法為準則調整均衡器抽頭系數，實現自適應的均衡[1]。

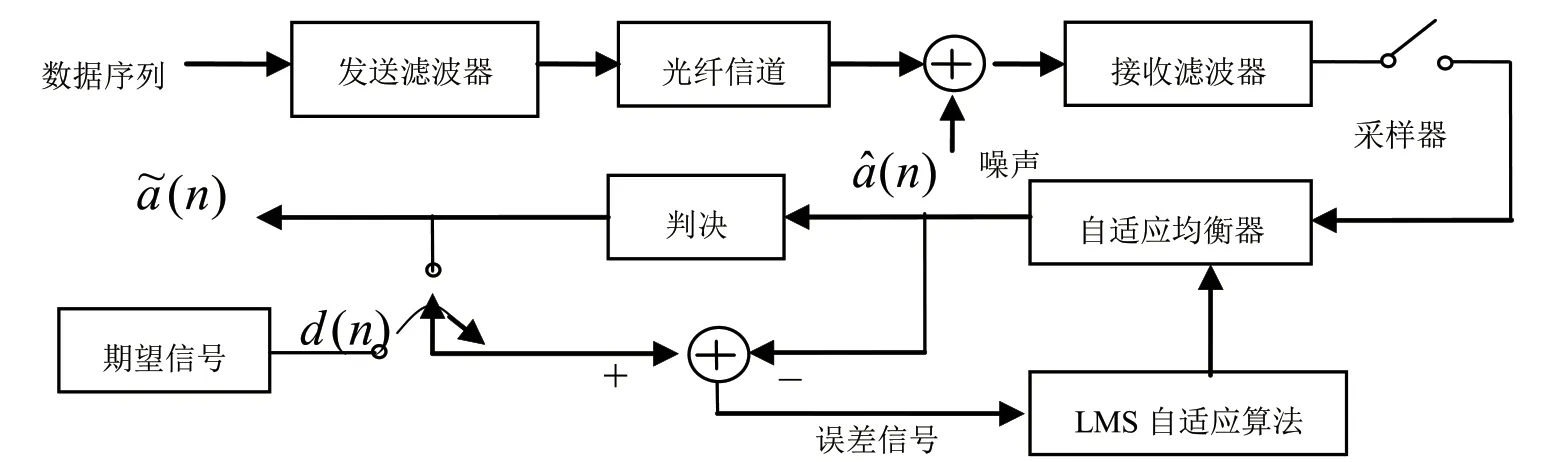
圖1 基于判決反饋結構的仿真框圖

2 判決反饋均衡器和LMS算法

LMS算法一般采用遞推的梯度（最陡下降）方法，用任意選擇的可調節濾波器系數作為開始，然后將每一新的輸入樣本輸入到這個自適應FIR濾波器，計算相應的輸出，形成誤差信號e(n)=d(n)-y(n)，并按方程

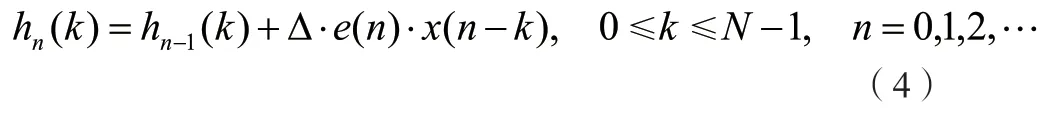
更新濾波器的系數，這里Δ 稱作步長參數，x(n-k) 是輸入信號在時間n上位于濾波器第k個抽頭上的樣本；而e(n)·x(n-k)是對第k個濾波器系數的一個梯度負值的近似估計，這就是為自適應的調節濾波器系數而使平方誤差e2(n)之和ε達到最小的LMS遞推算法。步長參數Δ 控制了達到最優解的算法收斂速率。傳統LMS算法基于固定步長，大的Δ 步長值會導致大的步長調節，從而加速收斂；而小的Δ 步長值會產生較慢的收斂，然而，如果Δ 值取得太大，算法會變的不穩定。為了保證穩定性，Δ 必須選在下面的范圍內

式中，N是自適應FIR濾波器的長度，Px是輸入信號的功率。

本文提出了一種基于二分法的可變步長算法，使得步長隨著迭代次數改變而改變。一開始步長較大，每次迭代步長變為原來的二分之一。這樣既保證了收斂速度，又保證了收斂的穩定性和均衡效果最佳，使得Δ 同時滿足公式（6）。

3 仿真結果

信道中加入指定信噪比的零均值高斯白噪聲。圖2（a）、（b）圖是基于二分法的可變步長的LMS算法均衡前后的眼圖，可以看出該算法也能有效的消除了碼間干擾（ISI）。

圖2 基于固定步長LMS和可變步長LMS算法的光纖信道均衡

其中（a）、（b）圖是固定步長LMS和基于二分法可變步長的LMS算法的誤差曲線。從兩張圖對比可以看出基于二分法可變步長的LMS算法有更快的收斂速度和更好的性能。固定步長LMS算法大概需要200多次迭代，而基于二分法可變補償的LMS算法只需要大概50次迭代左右。

4 結束語

算法簡單，易于實現是LMS算法的優點，缺點是收斂速度較慢，本文基于二分法可變步長LMS算法的提出有效解決了這個問題。使其更適用于對速度有更高要求的高速光纖信道均衡。