一種變量是梯形模糊數的兩層多隨從線性規劃模型及其算法
周喜華, 賈洪信, 黃曉紅, 鄧勝岳, 謝 亮
(1- 廣東環境保護工程職業學院基礎教育部,佛山 528216; 2- 湖南工業大學理學院,株洲 412007)
1 引言
Zadeh[1]在其發表的論文中首次運用模糊集合的概念,這標志著模糊數學的誕生.康托羅維奇[2]于1939 年,首次提出了線性規劃模型及其理論.Zimmermann[3]最早提出模糊線性規劃,并通過模糊線性規劃對稱模型的解法解決了約束模糊型問題.模糊線性規劃包含約束模糊型規劃、系數模糊型規劃及決策變量模糊型規劃[4,5].Candler 和Norton[6]于1977 年首先提出“多層規劃”模型及其理論,而二層規劃是多層規劃的基本組成形式,大量應用于兩層遞階特征的經濟管理系統(利用兩層多隨處規劃對上層為一個領導者、下層為多個隨從特征的遞階系統進行建模與仿真).鄧勝岳等[7,8]先后研究了系數或決策變量為三角模糊數的二層多隨處線性規劃模型,給出了可行的算法,并通過算例驗證了該算法的可行性和有效性.然而,梯形模糊數是三角模糊數的一般形式,能更好的模擬實際模糊環境,具有更廣泛的應用范圍.為了拓展模糊二層多隨處線性規劃模型的應用范圍,本文系統研究了一類決策變量為梯形模糊數的兩層多隨處線性規劃模型.因此,本文研究的模型是文獻[7]中模型的更一般形式.
2 基礎知識
2.1 模糊結構元理論
定義1[9,10]設E 為實數域R 上的模糊集合,而隸屬函數記為E(x), x ∈R.如果E(x)滿足下述性質:
1) E(0)=1;
2) 在區間[-1,0)上,E(x)是單調遞增的函數且右連續,在區間[0,1)上,E(x)是單調遞減的函數且左連續;
3) 若x <-1 或x >1 時,E(x)=0,則E 是實數域上的模糊結構元.
定義2[9,10]若模糊結構元E(-x)=E(x),則稱E 為對稱模糊結構元.
定義3[9,10]若模糊結構元E 滿足:
1) x ∈(-1,1), E(x)>0;
2) E(x)連續,且在[-1,0)上嚴格單調遞增,在[0,1)上嚴格單調遞減,則稱E 為正則模糊結構元.
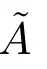

則根據E 可得到
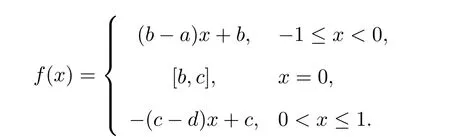

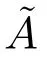
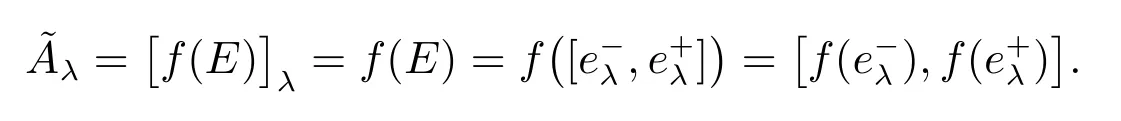
2.2 兩層多隨從線性規劃
兩層多隨從線性規劃模型(MFBLP)及引理
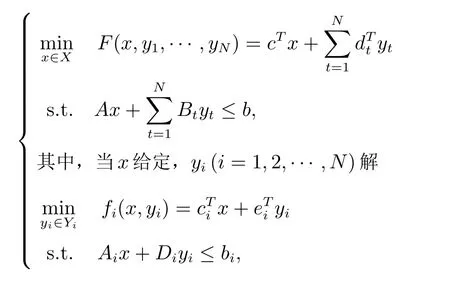

其中i=1,2,··· ,N.
3 一類變量為梯形模糊數的兩層多隨從線性規劃模型及算法
3.1 模型
一類變量為梯形模糊數的二層多隨從線性規劃模型,具體形式如下
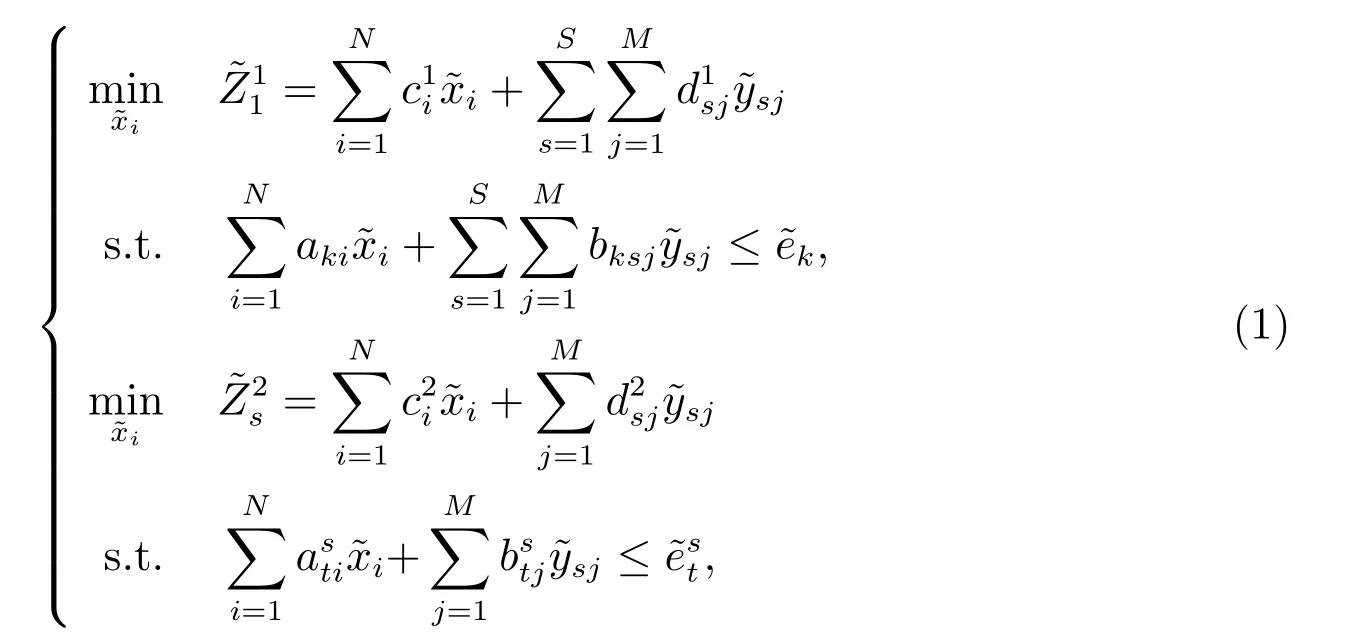



步驟3 根據定理1,將模型(1)的最優解轉化為模型(2)的最優解;
步驟4 根據引理5,并利用Matlab 編程運行得到定理1 中模型的最優解;
步驟5 將(2)的最優解代入(1)得到最優解.
4 算例
本節將提供兩個算例,其中算例1 為一個領導者一個隨從情形,算例2 為一個領導者兩個隨從情形,并且模型中的決策變量都用梯形模糊數表示.通過兩個算例的求解過程驗證了本文研究的模型及算法的可行性和有效性.當文中的模型決策變量由梯形模糊數退化為三角模糊數時,算法仍然可行,可見本文的模型是文獻[7]中模型的更一般形式.
算例1 考慮上層一個領導者、下層一個隨從,且上下層均有約束條件的一類變量為梯形模糊數的兩層線性規劃問題

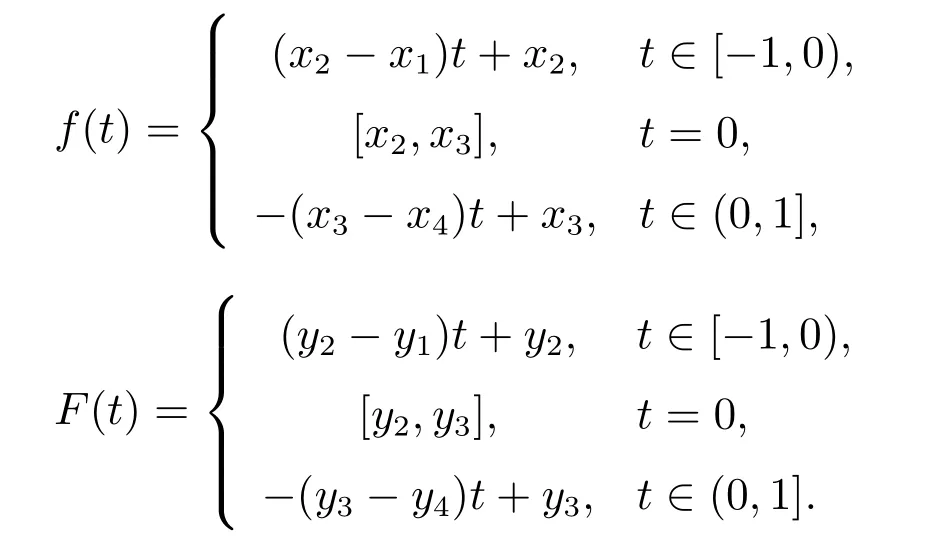

步驟2 E(t)為三角模糊結構元,則
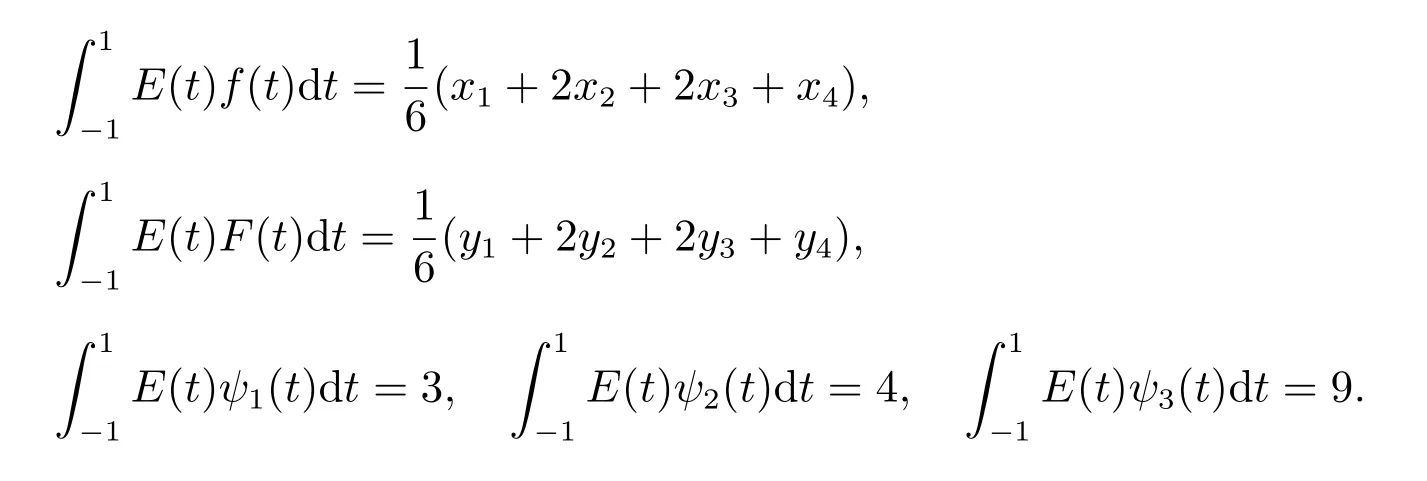
所以可以將原問題(3)轉化為下式
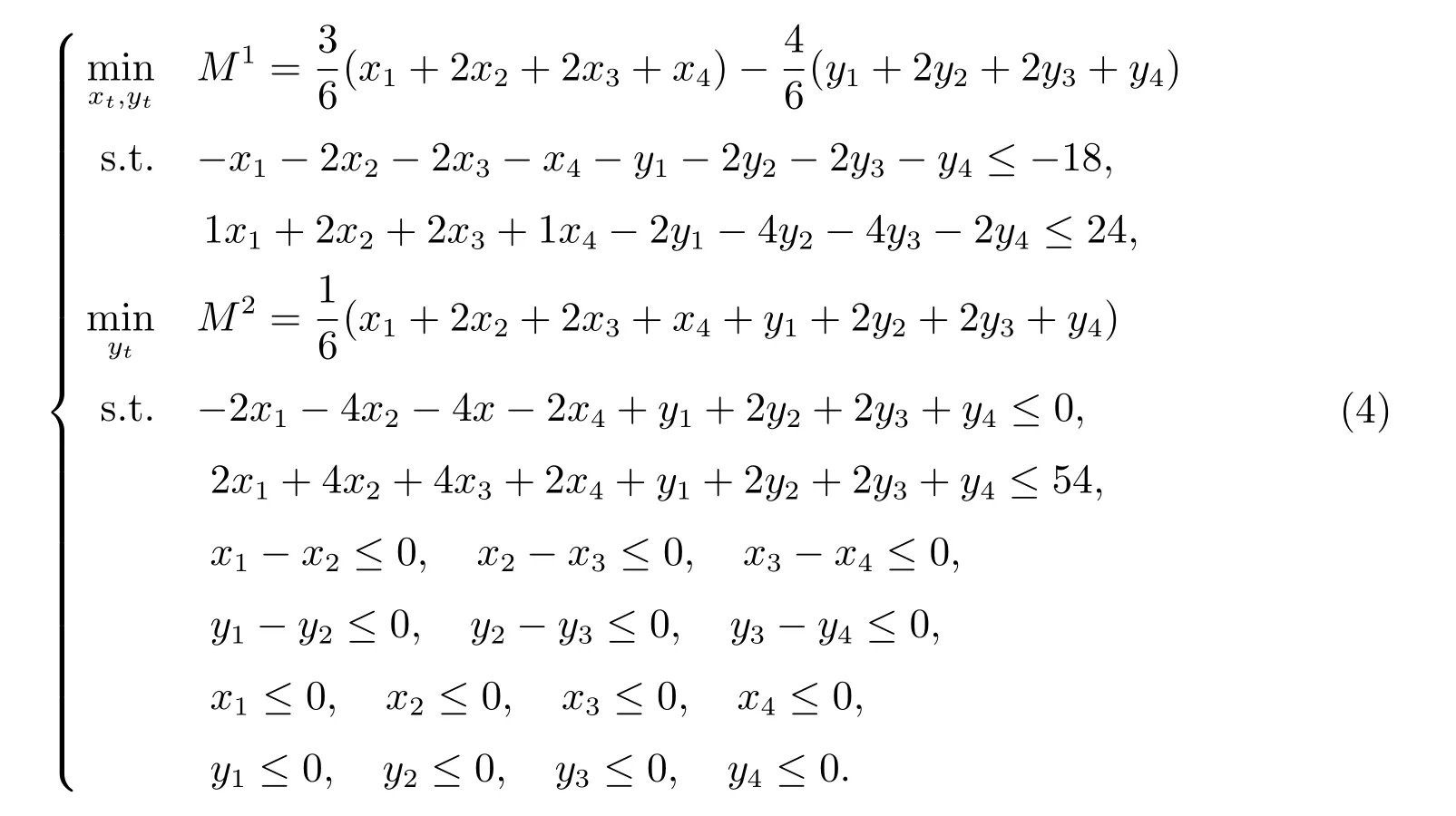
步驟3 由引理5 可知,若存u1, u2, v1, v2, v3, v4, v5∈R,且u1, u2, v1, v2, v3, v4,v5≥0,則有
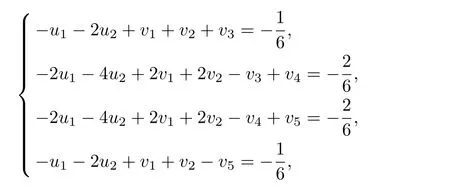
所以可以得到兩種情況:
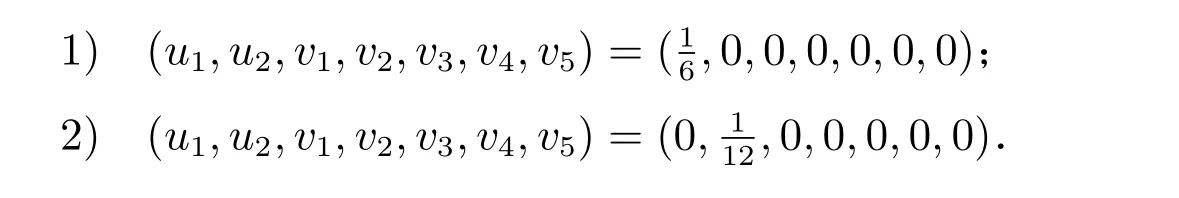
步驟4 若情況1)成立時,可將問題(4)轉化為
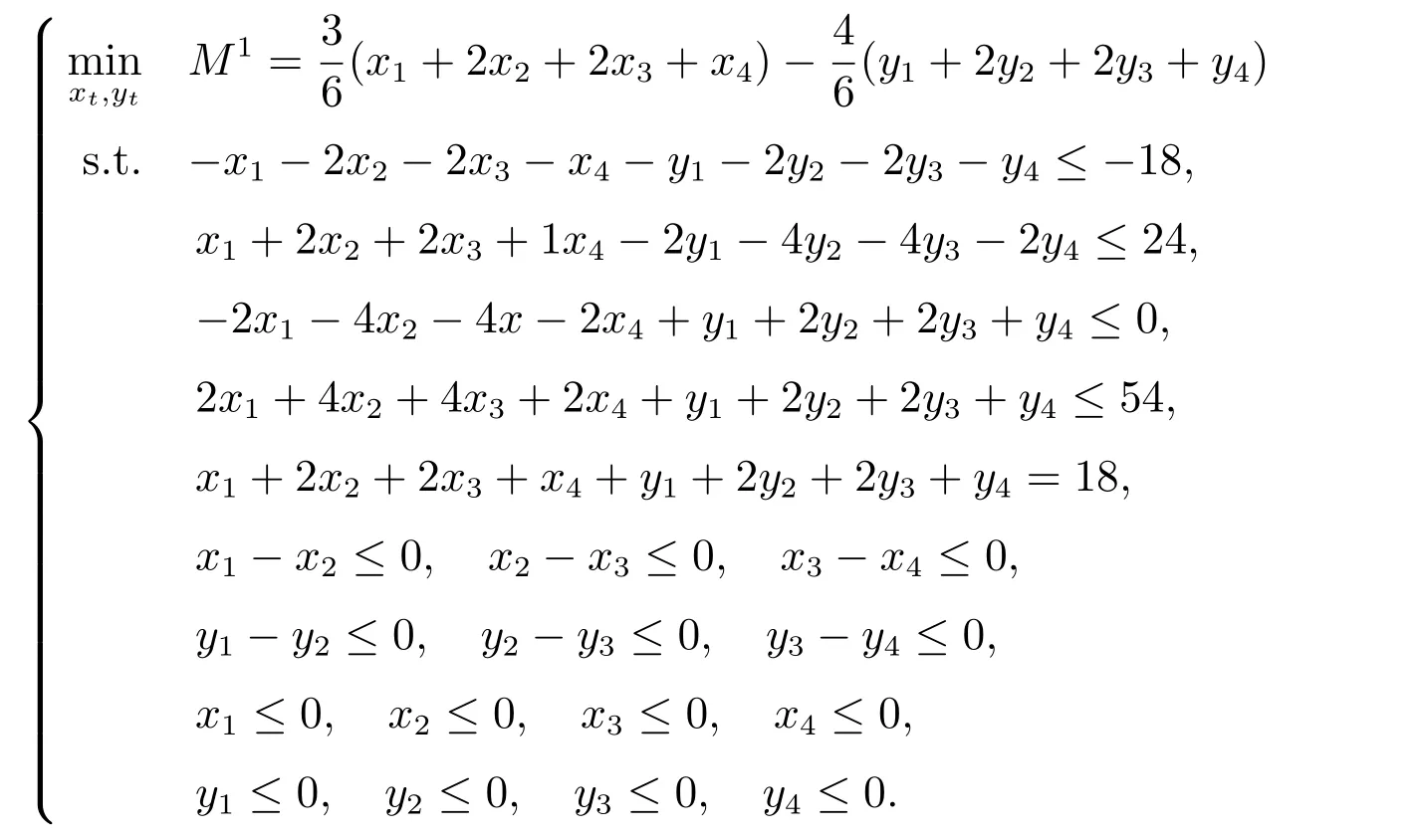
若情況2)成立,則同理可得.
步驟5 情況1)與情況2)所得到的最優值分別為-5.0000, 11.6000,所以情況1)的最優解為問題(4)的最優解,即為x1= 0.1687, x2= 0.2624, x3= 0.5996, x4= 4.1071,y1= 0.5407, y2= 0.9529, y3= 1.9843, y4= 5.5850.將上述結果代入原問題(3)得到:上層問題的最優解為(-10.0187,-6.1384,-3.0244,-1.6567),下層問題的最優解為(0.7094,1.2153,2.5839,9.6921).
算例2 考慮上層一個領導者、下層二個隨從,且上下層均有約束條件的一類變量為梯形模糊數的兩層多隨從線性規劃問題

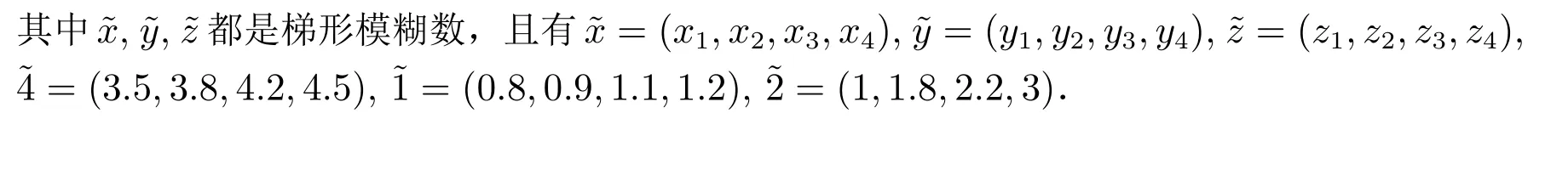
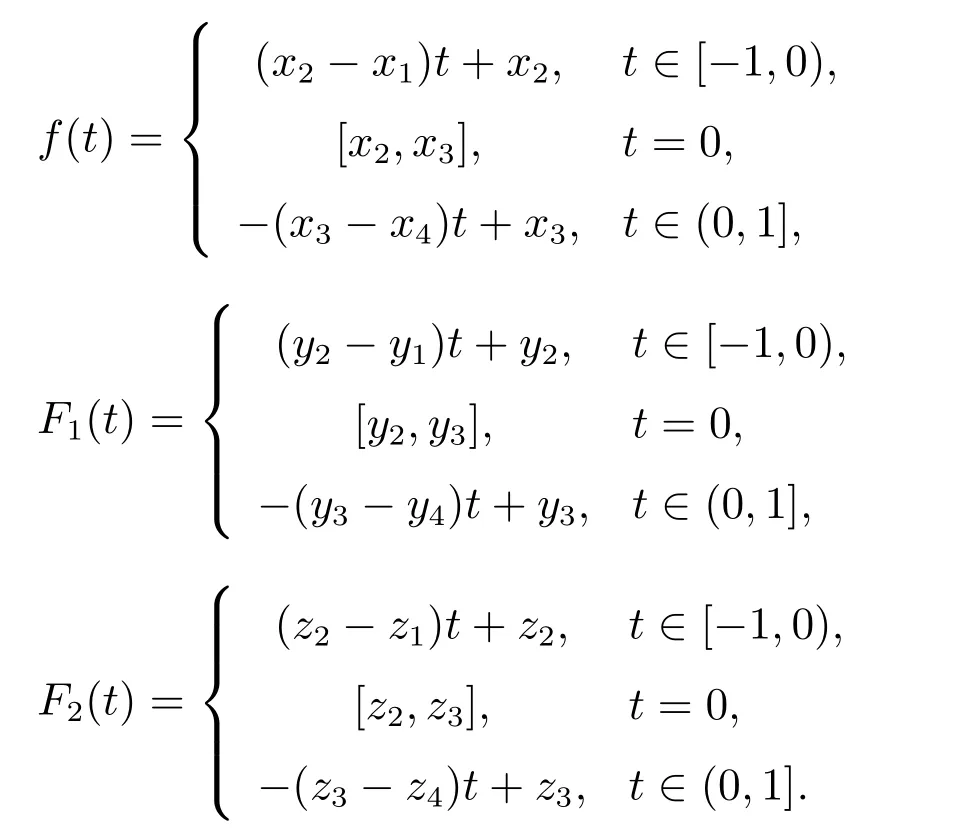

步驟2 E(t)為算法步驟一給出正則三角模糊結構元,則
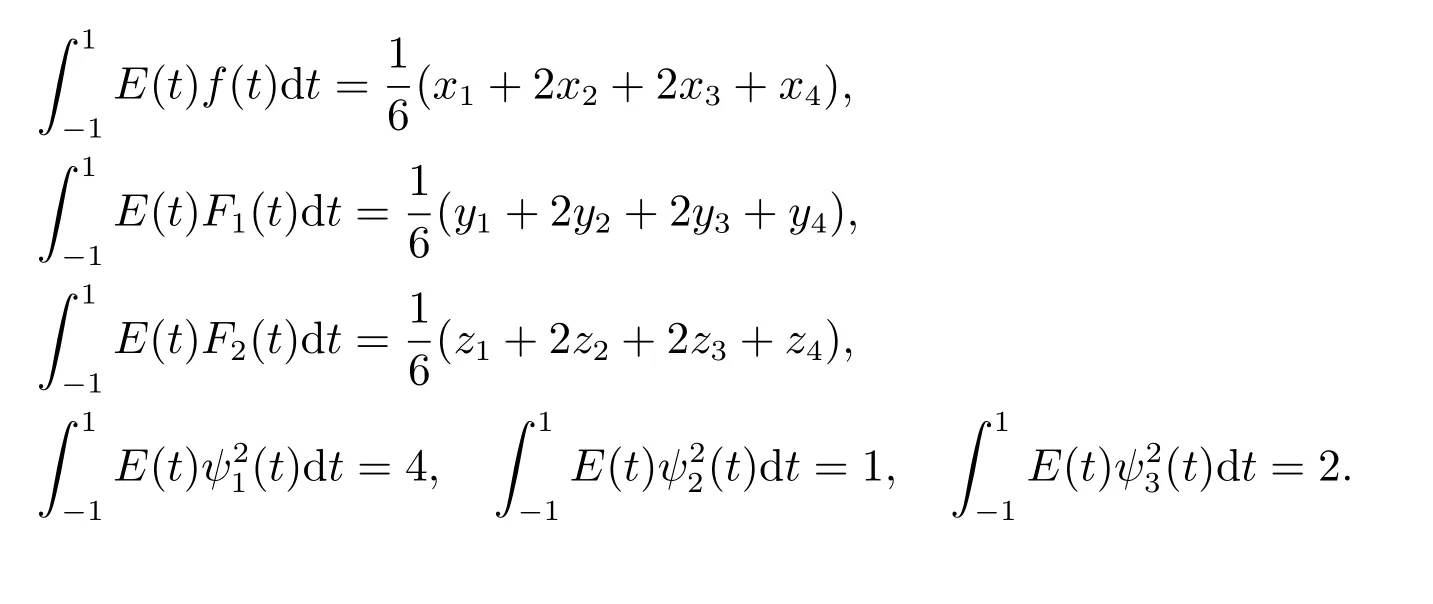
所以可以將原問題(5) 轉化為下
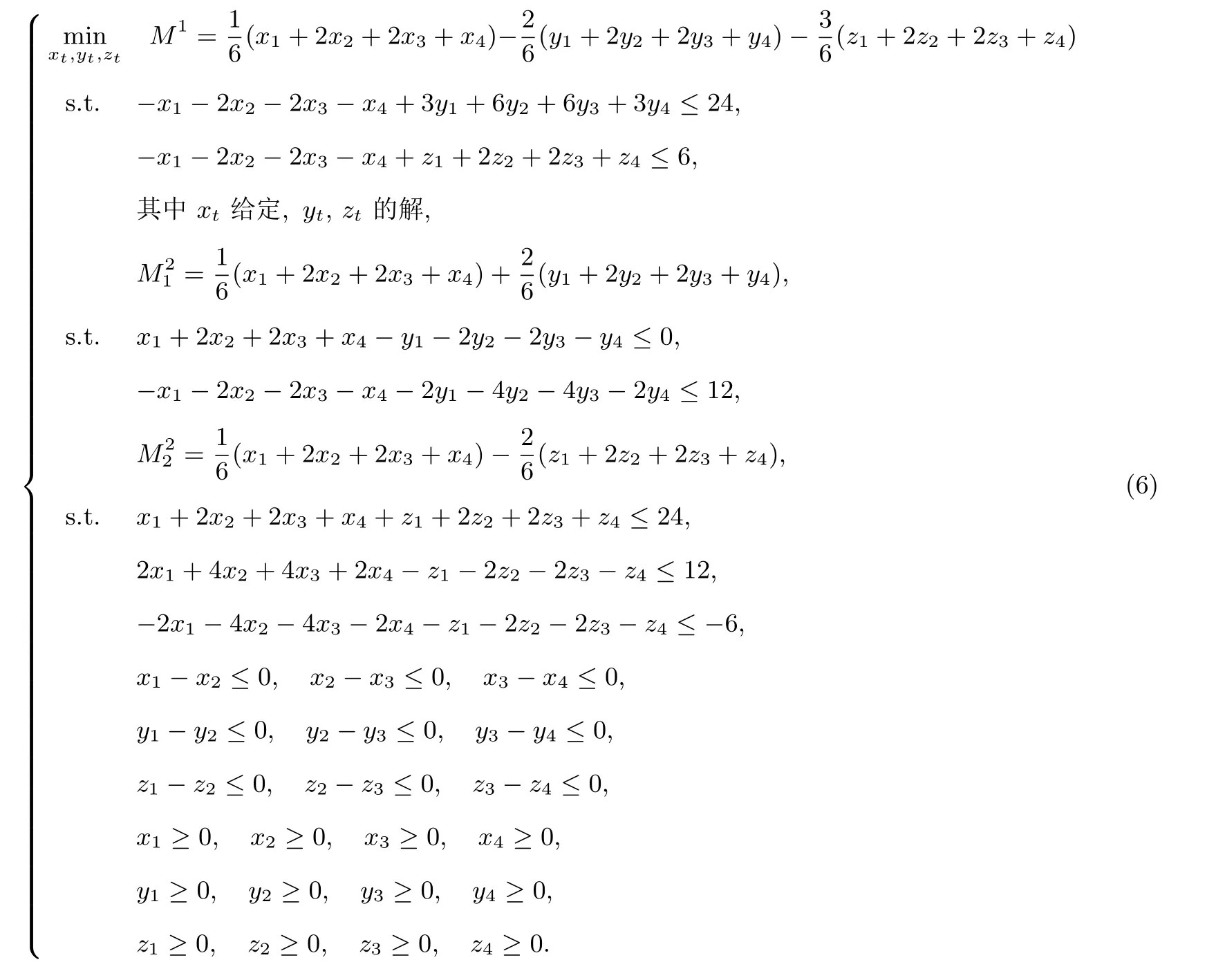
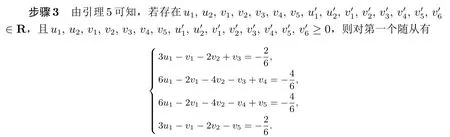
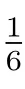
對第二個隨從有
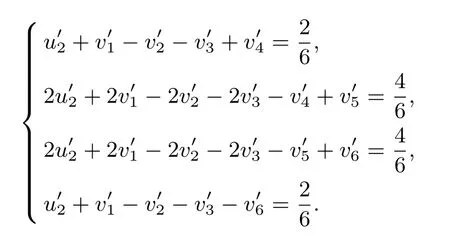

步驟4 若情況一成立,可將問題(6)轉化為
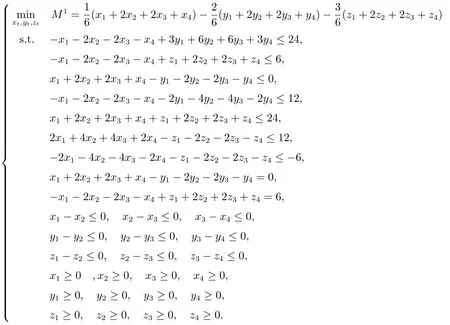
若情況二、情況三、情況四成立,同理可得.
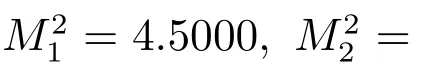
5 結論
針對一類變量為梯形模糊數的兩層多隨從線性規劃問題,利用模糊結構元的性質,將梯形模糊數進行模糊數的結構元加權序處理,到達了去模糊化的目的,從而使得一類變量為梯形模糊數的兩層多隨從線性規劃轉化為兩層多隨從線性規劃,提出了算法,并通過算例驗證了該算法的可行性.

