一類改進的GOM(1,1)模型及其應用

張 鍇, 王成勇, 賀麗娟,?

(1- 文華學院數學科學系，武漢 430074; 2- 湖北文理學院數學與統計學院，襄陽 441053)

1 引言

灰色預測模型[1]因建模過程簡單，并且在能夠在樣本數據量較小的情況下，得到較為準確的擬合與預測結果，已被廣泛應用于交通管理、城市環境、生態農業、能源分析等眾多領域[2-4].與傳統灰色預測模型不同，GOM(1,1)模型(Grey Opposite-direction Model)[5,6]是基于反向累加生成方法所建立的灰色預測模型，對于具有遞減性質的數據序列具有較好的擬合與預測效果.近年來，許多學者從不同角度對GOM(1,1)模型進行了改進，楊知等[7]分析了反向累加生成，改進了模型背景值的計算，給出了GOM(1,1)模型參數求解的優化方法.陳鵬宇[8]根據背景值的幾何意義，建立了兩種加權背景值的構造形式.練鄭偉等[9]在反向累加條件下，對原始序列和生成序列的齊次和非齊次指數特性進行了研究，在此基礎上建立了新的GOM(1,1)模型.文獻[10-12]將改進的GOM 模型用于沉降預測，文獻[13]將優化的GOM 模型用于道路交通事故預測，都取得了不錯的效果.

值得注意的是，上述眾多文獻中，均用常數b 表示灰作用量，將來自外部的擾動視作不變，這樣處理可以簡化模型計算，卻不能較好反映數據發展變化的客觀規律.實際上，隨著時間和空間的變化，灰色作用量也會隨之變化[14-16].本文重視建模過程中灰作用量的動態變化過程，從白化微分方程入手，在一次累加生成序列滿足非齊次指數律的條件下，通過積分給出了GOM(1,1)模型的優化背景值，以原始序列和模擬序列的平均相對誤差平方和最小為原則，確定時間響應函數中的最優參數，最終形成完整的優化GOM(1,1)模型.

2 反向累加生成及GOM(1,1)灰色預測模型

定義1[5,6]設x(0)=(x(0)(1),x(0)(2),··· ,x(0)(n))為原始序列，令

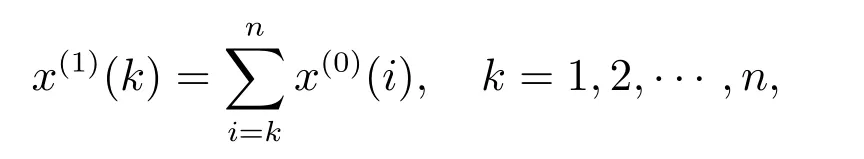
稱x(1)=(x(1)(1),x(1)(2),··· ,x(1)(n))為x(0)的一次反向累加生成序列.

定義2[5,6]設x(0)=(x(0)(1),x(0)(2),··· ,x(0)(n))為原始序列，取

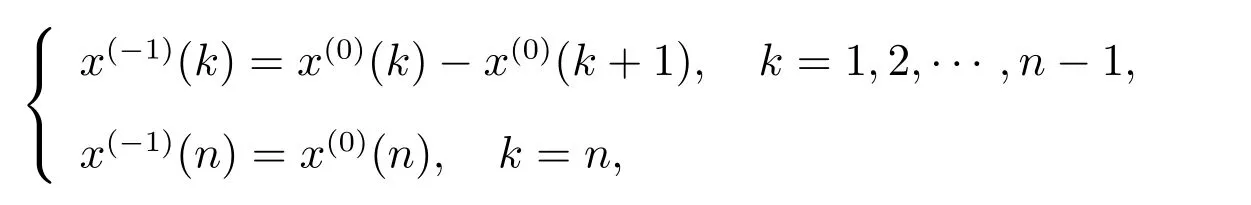
稱x(-1)=(x(-1)(1),x(-1)(2),··· ,x(-1)(n))為x(0)的一次反向累減生成序列.

易知

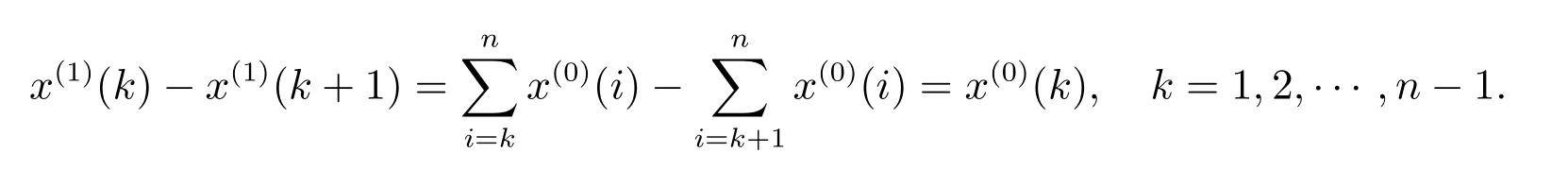
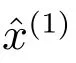
定義3[9]設x(0)為非負準光滑原始序列，x(1)為其一次反向累加生成序列，對x(1)建立基于反向累加生成的GOM(1,1)模型

-x(0)(k-1)+az(1)(k)=b, k =2,3,··· ,n,

其中a 為發展系數，b 為控制系數，z(1)(k)為背景值.

GOM(1,1)模型的白化方程為

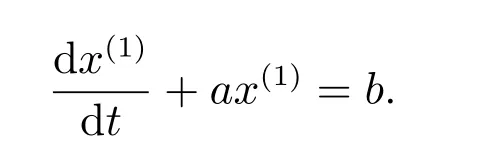
定義3 中的模型用常數b 表示灰作用量，并未考慮灰作用量隨時間和空間的變化而發展變化的過程；如果將灰作用量近似看作為時間的線性函數，即使用b1+b2k 代替原來的灰作用量，可以對GOM(1,1)模型進行優化.

3 GOM(1,1)灰色預測模型的優化

3.1 灰作用量優化的GOM(1,1)灰色預測模型

定義4 設x(0)為非負的原始序列，x(1)為其一次反向累加生成序列，稱

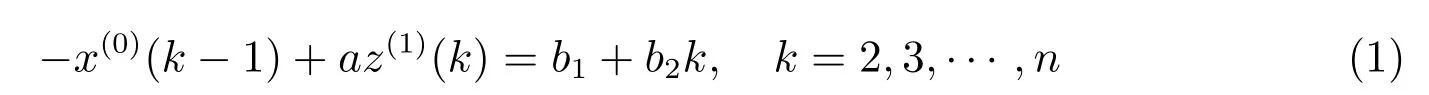
為灰作用量優化的GOM(1,1)模型.

定義5 稱

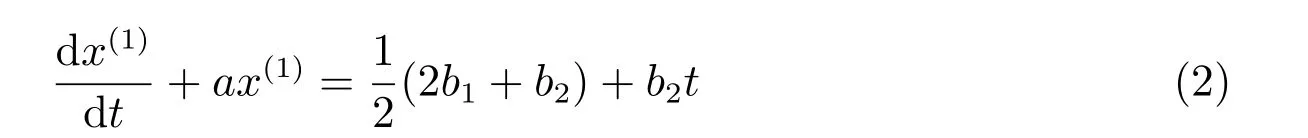
為灰作用量優化的GOM(1,1)模型的白化方程.

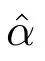
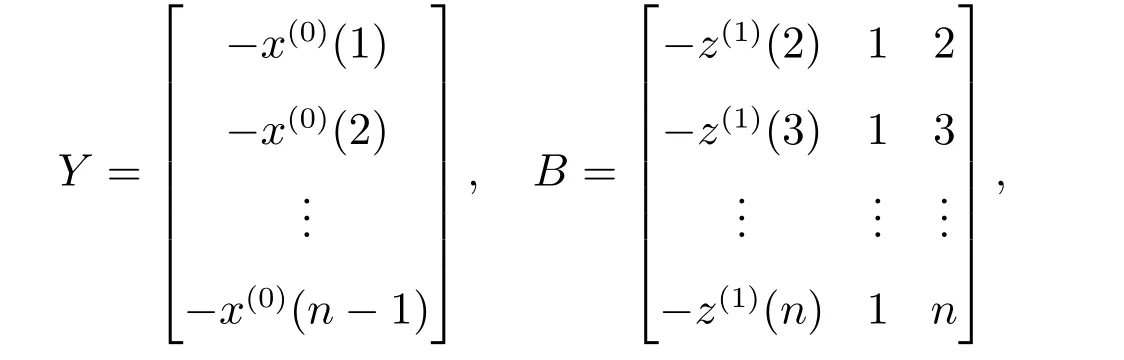
則GOM(1,1)模型(1)的參數估計式為

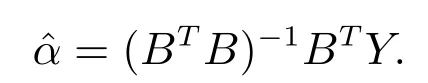
證明 將數據代入灰色微分方程-x(0)(k-1)+az(1)(k)=b1+b2k，移項得到

-x(0)(1)=-az(1)(2)+b1+2b2,

-x(0)(2)=-az(1)(3)+b1+3b2,

··· ,

-x(0)(n-1)=-az(1)(n)+b1+nb2,

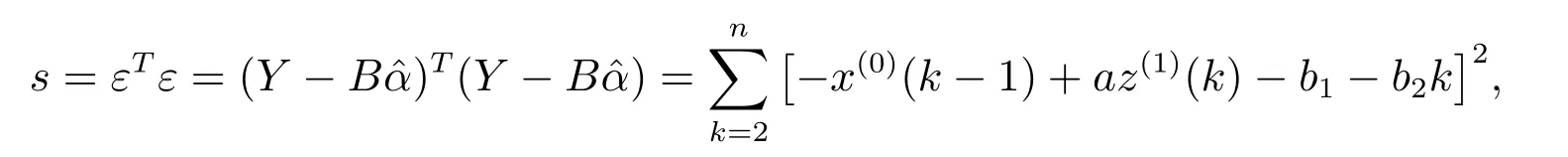
使s 最小的a, b1, b2應滿足

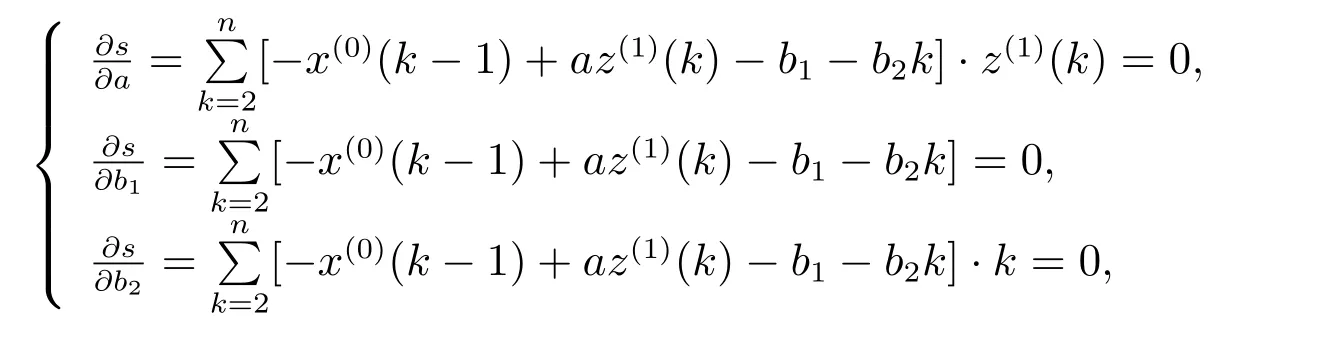
3.2 GOM(1,1)灰色預測模型背景值的優化

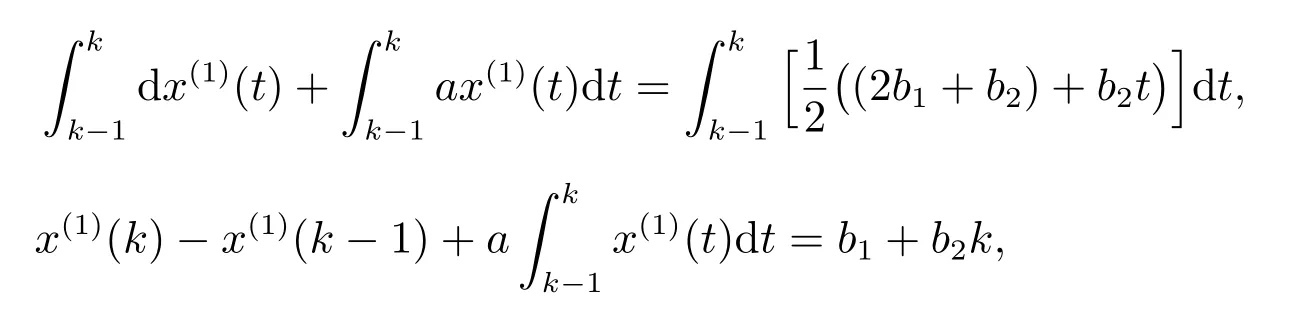
即

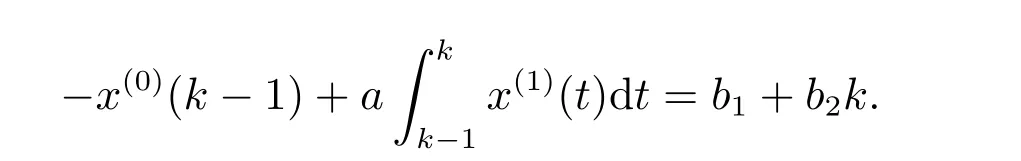
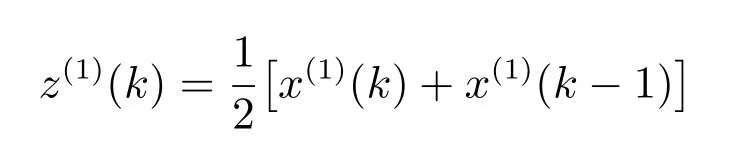
會具有更好的適應性.

定理3 x(0), x(1)如定義4 所示，若x(1)滿足非齊次指數形式，則背景值為

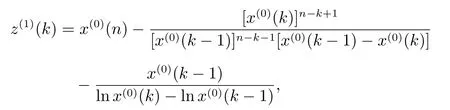
其中k =2,3,··· ,n，且x(0)(k)/=x(0)(k-1).

證明 x(1)滿足非齊次指數形式，不妨假設

x(1)(t)=AeBt+C,

其中A, B, C 為待定系數，背景值化簡可得

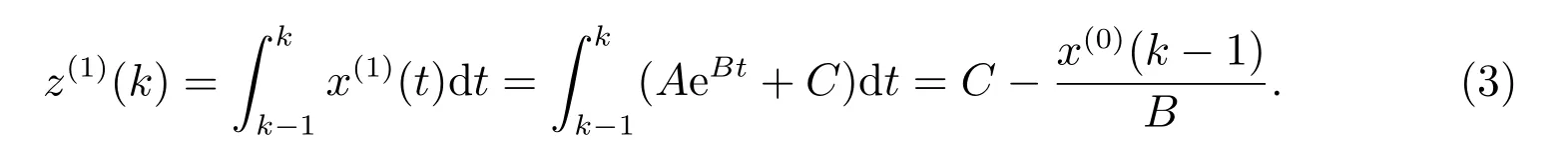
由于

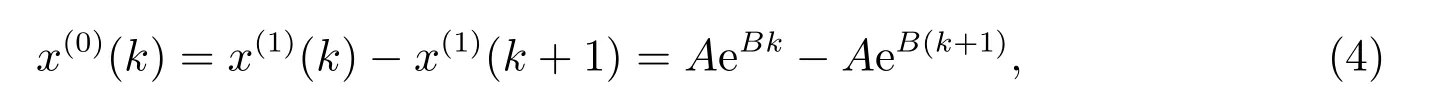
則

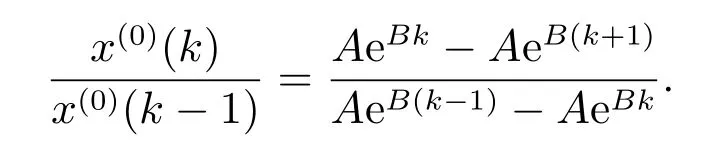
從而

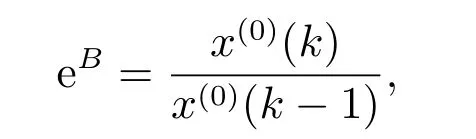
即

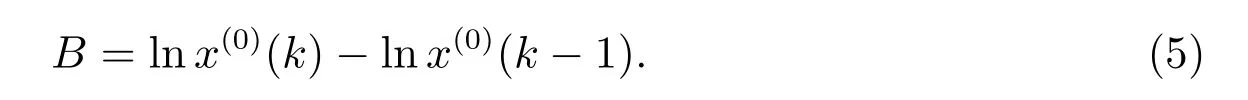
又由(4)式，可得

根據原始序列x(0)與一次反向累加生成序列x(1)的關系，當n = k 時，有x(1)(n) =x(0)(n)，即x(1)(n) = x(0)(n) = AeBt+C，得到C = x(0)(n)-AeBt，將(5),(6)式代入，則有

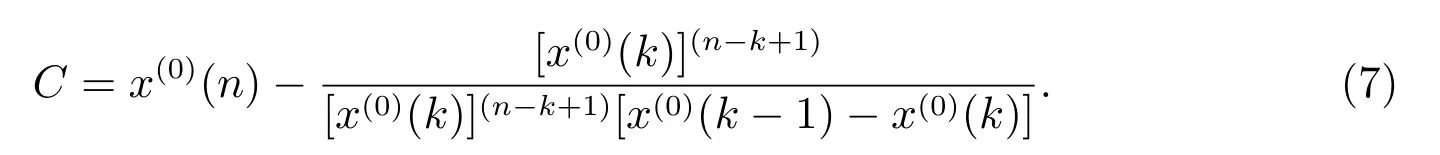
將(5)-(7)式代入(3)式整理可得定理結論.

3.3 初始條件的改進

傳統GOM(1,1)模型選擇初值時，認為擬合曲線一定通過點(1,x(1)(1))或(1,x(1)(n))，這種強制擬合曲線通過原始數據序列中的某個數據點的方法缺乏相應的理論基礎，建立的模型預測誤差較大.為了改進上述不足，本文以原始序列和模擬序列的平均相對誤差平方和最小為原則[17]，確定時間響應函數中的最優常數C1.

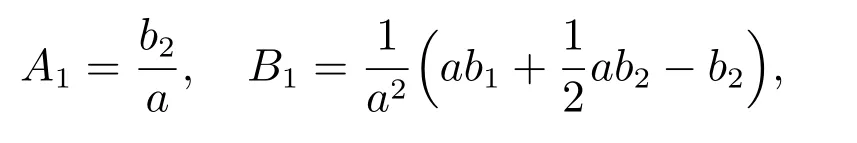
則

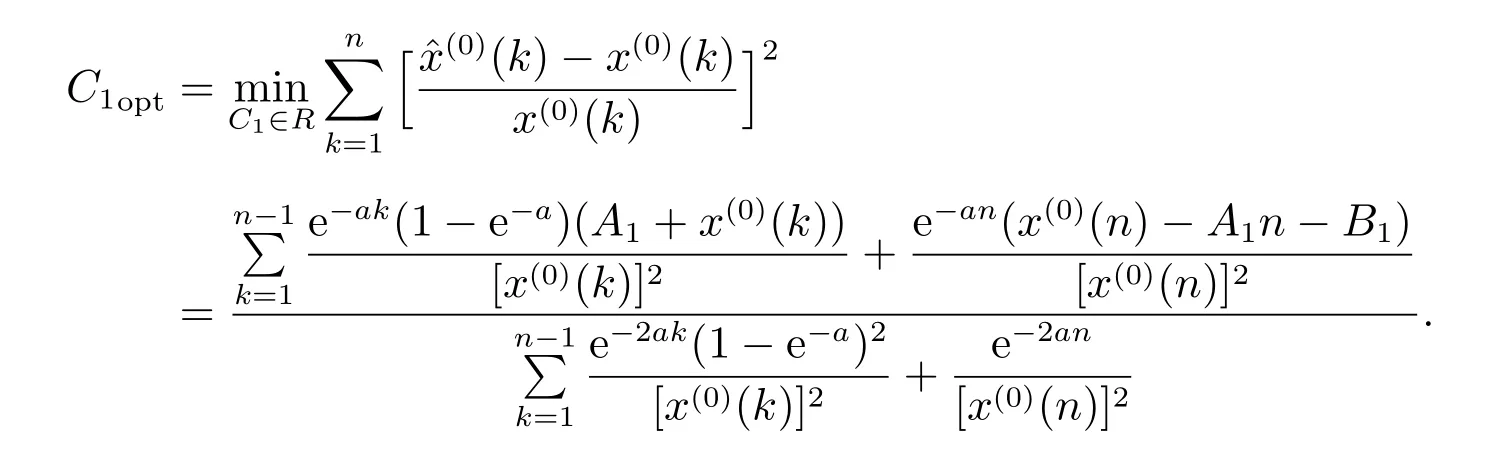
證明 邊值條件未知時

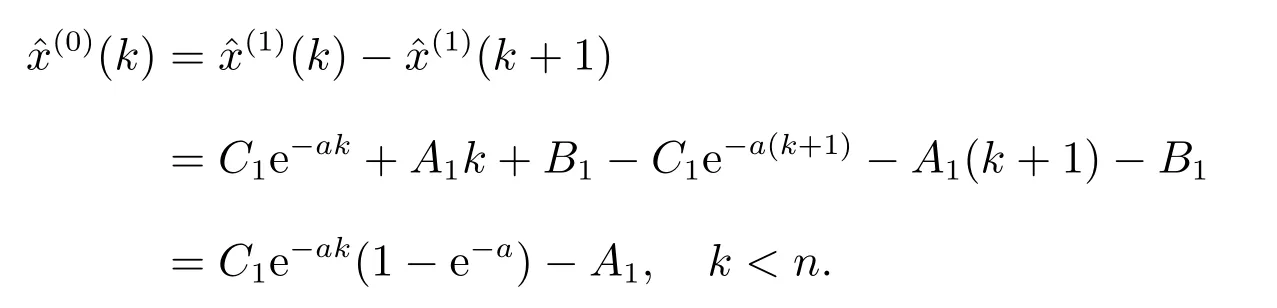
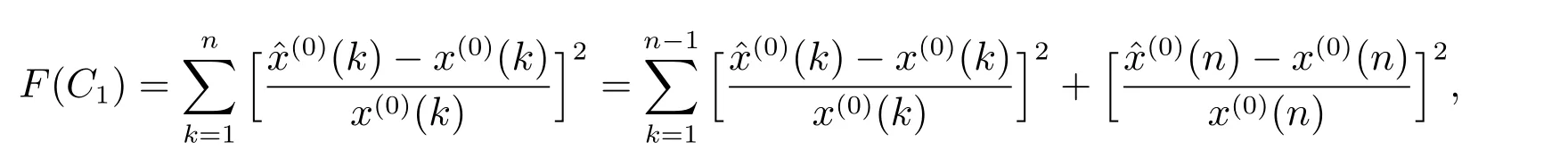
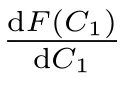
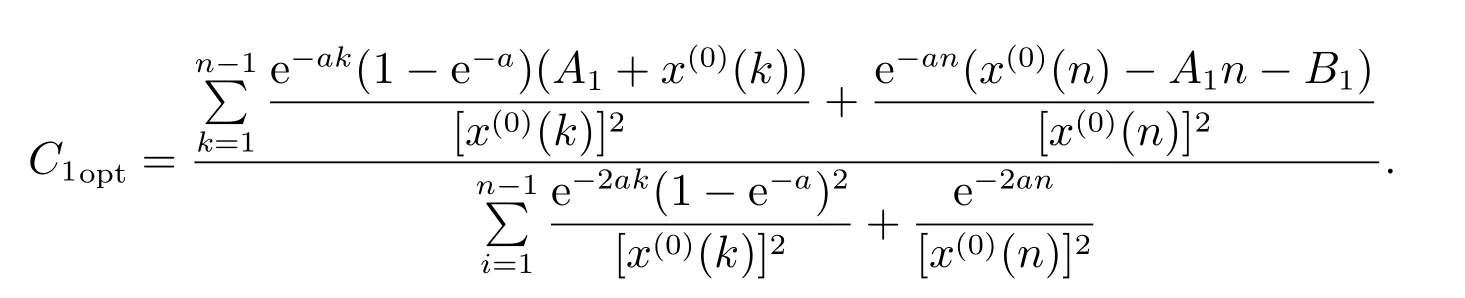
因此，改進GOM(1,1)模型的白化方程的時間響應式為

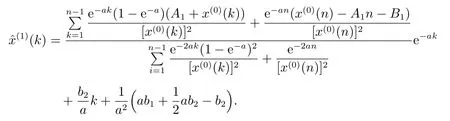
完整的GOM(1,1)模型改進算法如下：

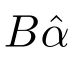
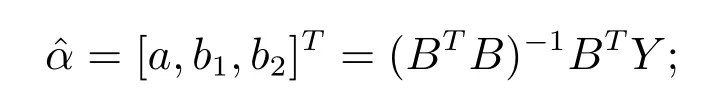
② 根據定理4，構造指標函數F(C1)，確定最優常數C1；

③ 將①、②中的參數估計式代入累減還原式，可得序列還原值的估計值.

4 實例

一種害蟲在某農藥作用下單位面積內的數量隨時間變化的采樣數據，見表1[6].

表1 采樣數據

設x(0)=(8,6.5,5.2,4.5,3.2)，一次反向累加生成序列x(1)=(27.4,19.4,12.9,7.7,3.2).傳統灰色模型的時間響應式

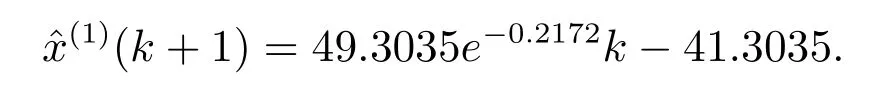
文獻[6]模型的時間響應式

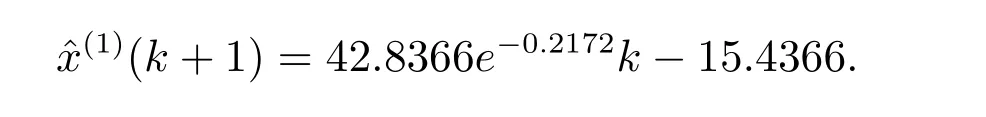
文獻[7]模型的時間響應式

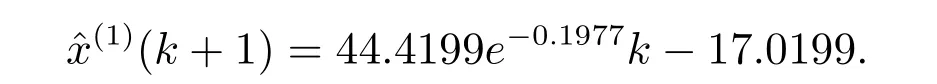
本文模型的時間響應式

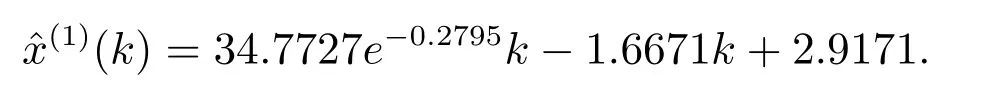
從表2 的數據對比中可以看到，傳統灰色模型的平均相對誤差最大，說明使用累加生成方法處理具有遞減趨勢的數據序列，建模預測的適應性較差，導致建模誤差較大；文獻[6]提出了反向累加生成概念，由此建立了對于具有單調遞減趨勢序列的反向累加灰色GOM(1,1)模型，由于忽略了背景值的構造會影響建模精度，平均相對誤差僅為1.67%；文獻[7]發現了GOM(1,1)模型的缺陷，對背景值進行了優化，但卻忽略了新背景值的建模適應性，導致對于本文實例中的數據序列建模效果不佳；本文優化模型的平均相對誤差僅為1.17%，相對于其他幾種模型的模擬精度有較大提升，能夠說明改進算法后的新模型更有優勢.

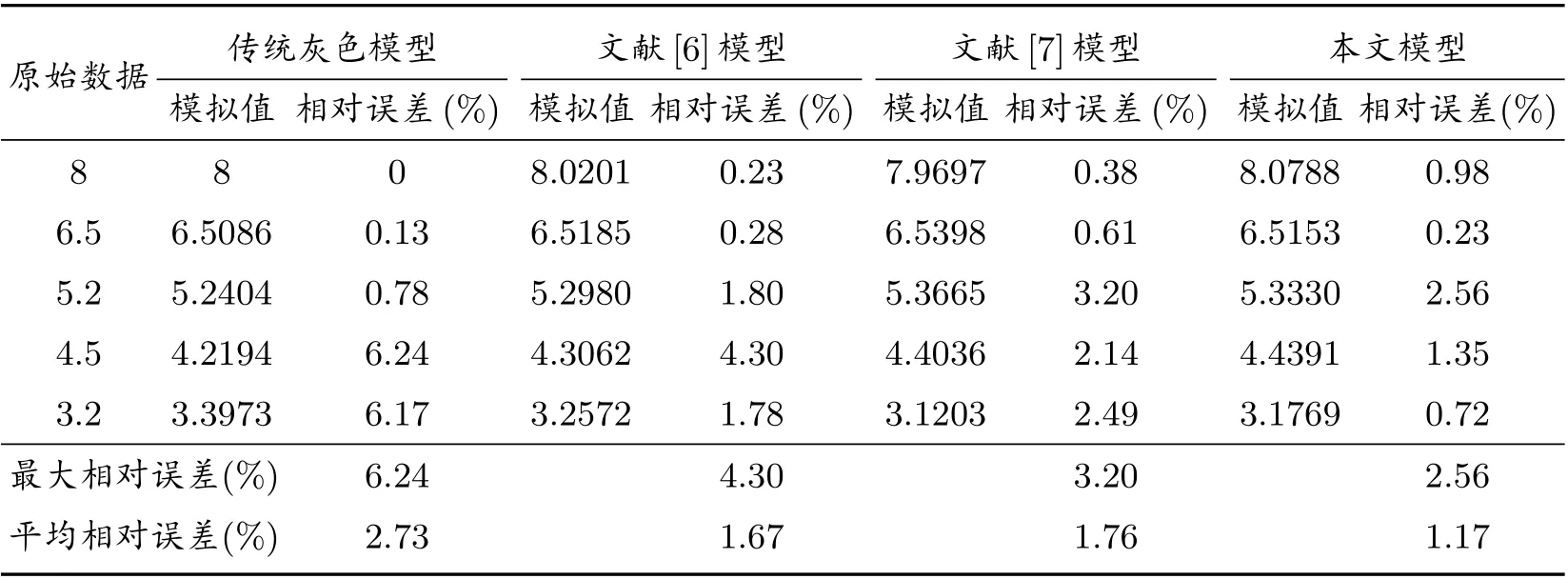
表2 四種模型的擬合結果和相對誤差對比

關于模型精度的檢驗，采用精度檢驗等級的方法[1]來說明模型的優良性：

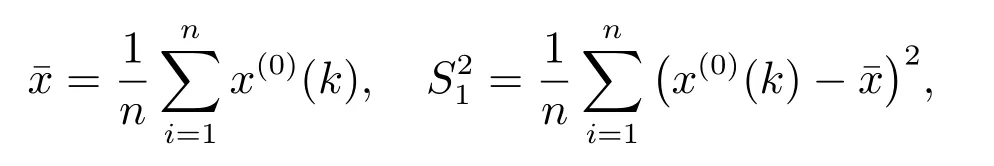
殘差的均值、方差分別為

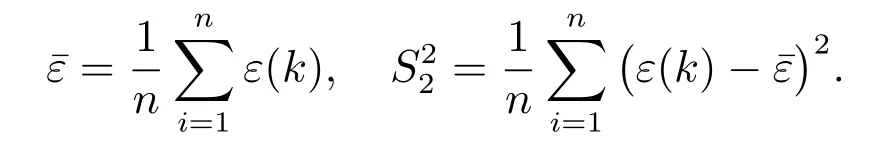
按照C 和p 的計算結果，參照表3 的具體指標對模型的精度進行評定.

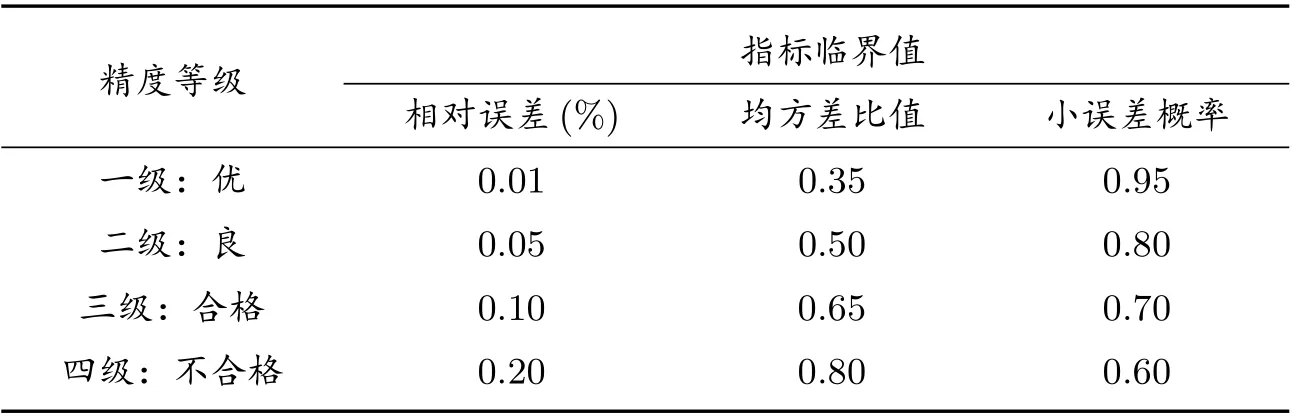
表3 精度檢驗等級參考表

經過計算，本文模型的均方差比值為0.0422，小誤差概率為1，根據表3 提供的精度檢驗等級參考表，模型精度等級為一級，表明該模型具有較高的模擬精度，可以用于中長期的預測.

5 結束語

本文從以下三方面提出了一個完整的GOM(1,1)模型改進算法：

1) 采用反向累加生成，考慮灰作用量的動態變化過程，建立了灰作用量的優化的GOM(1,1)模型；通過使用最小二乘法，得到了模型的未知參數估計式，并推導確定了時間響應函數的最優表達式；

2) 由背景值的幾何意義，基于一次累加生成序列滿足非齊次指數律的條件下，通過積分推導給出了GOM(1,1)模型的優化背景值，用以代替傳統GOM(1,1)模型的背景值；

3) 以原始序列和模擬序列的平均相對誤差平方和最小為原則，確定模型最優的初始條件，最終形成完整的GOM(1,1)模型改進算法.