復值耦合神經網絡的漸近和有限時間聚同步
李夢月,李必文
(湖北師范大學 數學與統計學院,湖北 黃石 435002)
0 引言
自Pecora L M和Carroll T L[1]引入混沌同步以來,同步在神經網絡方面的研究已然成為一個熱門的課題。聚同步即屬于同一個集群的個體完全同步,來自不同集群的個體不同步。作為一種更復雜的同步模式,近年來對于它的研究已涉及到了很多領域,如萬維網絡、電網網絡和細胞神經網絡等[2,3]。Cao Jinde等人[4]研究了具有時滯的混合耦合神經網絡的聚同步問題,通過構造特殊的耦合矩陣,提出了實現聚同步的新方法。文獻[5]討論了復雜網絡在有限時間的隨機同步問題,利用有限時間穩定性理論和不等式技巧,得到了保證復雜網絡在有限時間內實現隨機同步的充分條件。Liu Peng等人[6]從整數階的集群同步拓展到分數階,研究了具有時滯的分數階耦合神經網絡的漸近和有限時間聚同步問題,通過引入分數階微分系統的穩定性理論和Filippov正則化框架,得到了實現分數階耦合神經網絡漸近和有限時間聚同步的充分條件。更多的結果可參看文獻[7~10]。值得注意的是這些研究主要是實值神經網絡。
在大量的實際應用中,復信號經常出現,實值網絡不易解決此類問題,因此對復值網絡的研究變得極為重要。在各領域研究者的不懈努力與探索下,復值神經網絡已基本建立,并且在眾多領域有著廣泛的應用,如聯想記憶、圖像處理和通信[11~14]等。復值神經網絡作為實值神經網絡的一種擴展,它有更復雜的狀態,權值矩陣,激活函數等。它能解決更為復雜的問題,如單一實值神經元無法解決的XOR問題和探測對稱問題。從而對復值神經網絡的動力學研究是十分重要的,目前對復值神經網絡的研究包括平衡點的存在唯一性[15]、各種穩定性問題[16~21]和各種同步問題等。值得注意的是,雖然近年來對復值神經網絡的同步問題已有不少研究,如文獻[22]研究了具有離散和分布式的兩個加性時變時滯的復值神經網絡的同步,并基于矩陣不等式和倒凸方法,得到了確定復值神經網絡主從全局同步的準則。Chen jie jie等人[23]研究了具有時滯的分數階復值憶阻神經網絡的全局漸近穩定和自適應最終Mittag-Leffler同步。在文獻[24]中,Zhang wei wei等人通過構造合適的Lyapunov函數,利用分數階比較原理,建立了具有遺漏時滯分數階復值神經網絡同步的一些準則等。但是關于復值神經網絡聚同步這方面的研究還比較少。
在實際生活中時滯幾乎是無法避免的,尤其是在信號傳輸的過程中,由于放大器的切換速度有限,神經網絡不可避免的會有延遲,這會給神經網絡造成震蕩、分岔、不穩定等問題,從而影響神經網絡的動力學行為,因此討論具有時滯神經網絡的動力學行為十分重要。
基于以上討論,本文的目的旨在研究具有時變時滯的復值耦合神經網絡的聚同步問題。利用Halanay不等式,Filippov解的框架和微分包含原理,得到了復值耦合神經網絡在相應控制策略下實現漸近和有限時間聚同步的充分條件。本文余下部分組織如下,第一節是對本文符號進行說明和模型的描述。第二節給出了本文的主要結果。在第三節中用兩個數值例子說明了我們所得結果的有效性。最后一節給出結論。
1 準備工作
1.1 符號說明
C([t0-τ,t0],n)表示具有一致收斂拓撲的從區間[t0-τ,t0]到n連續函數的Banach空間。QR和QI分別表示矩陣Q∈m×n的實部和虛部。
1.2 模型描述
用Ω={N,ε,G}表示有節點集N={1,2,…,N}(∈+,N>2),邊集ε?N×N和耦合矩陣
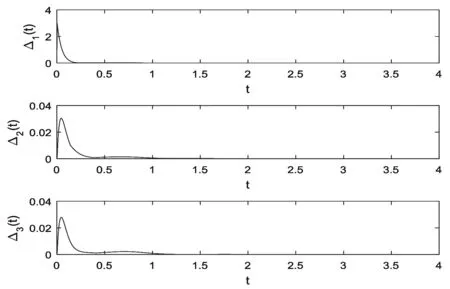
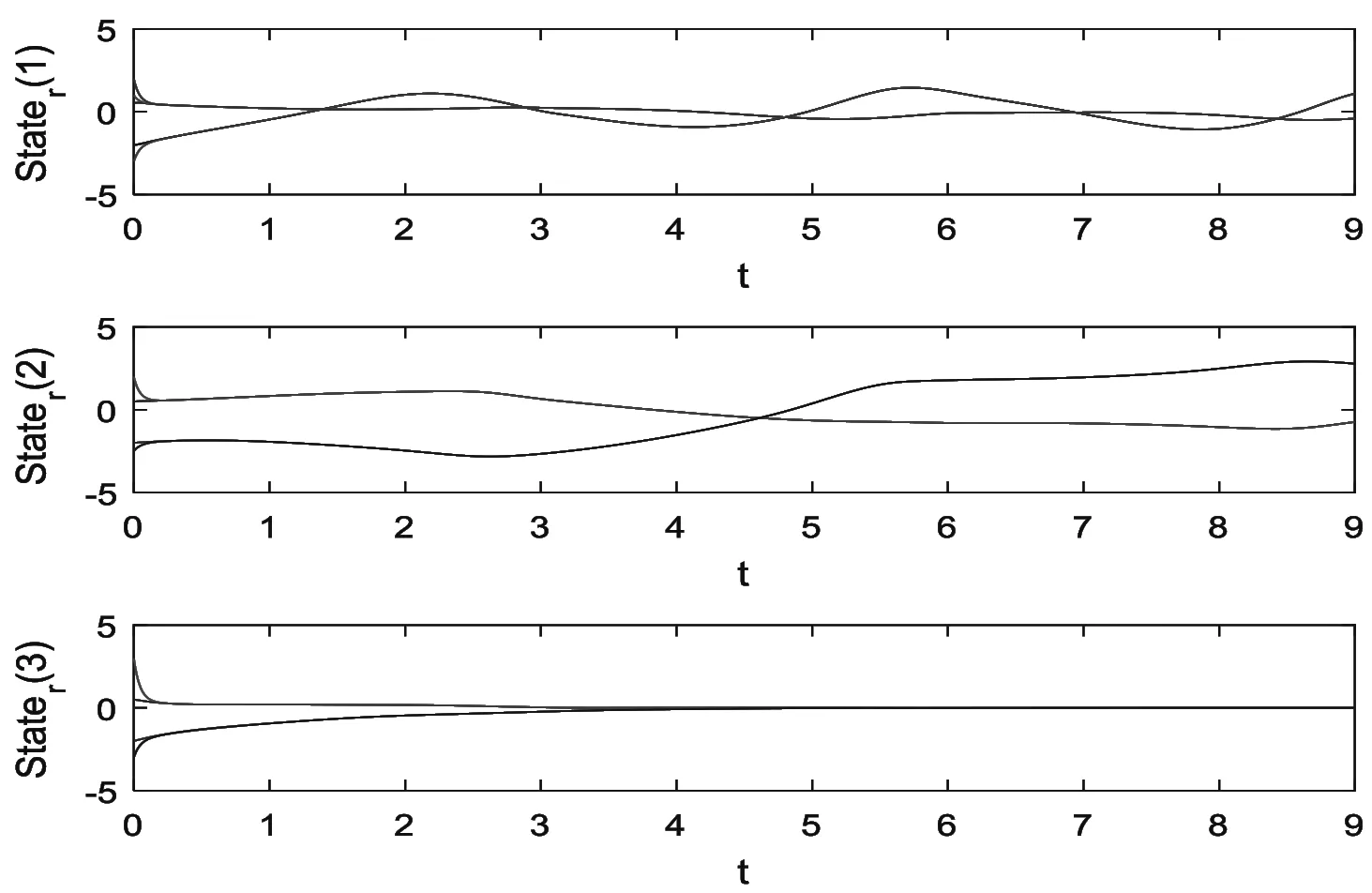
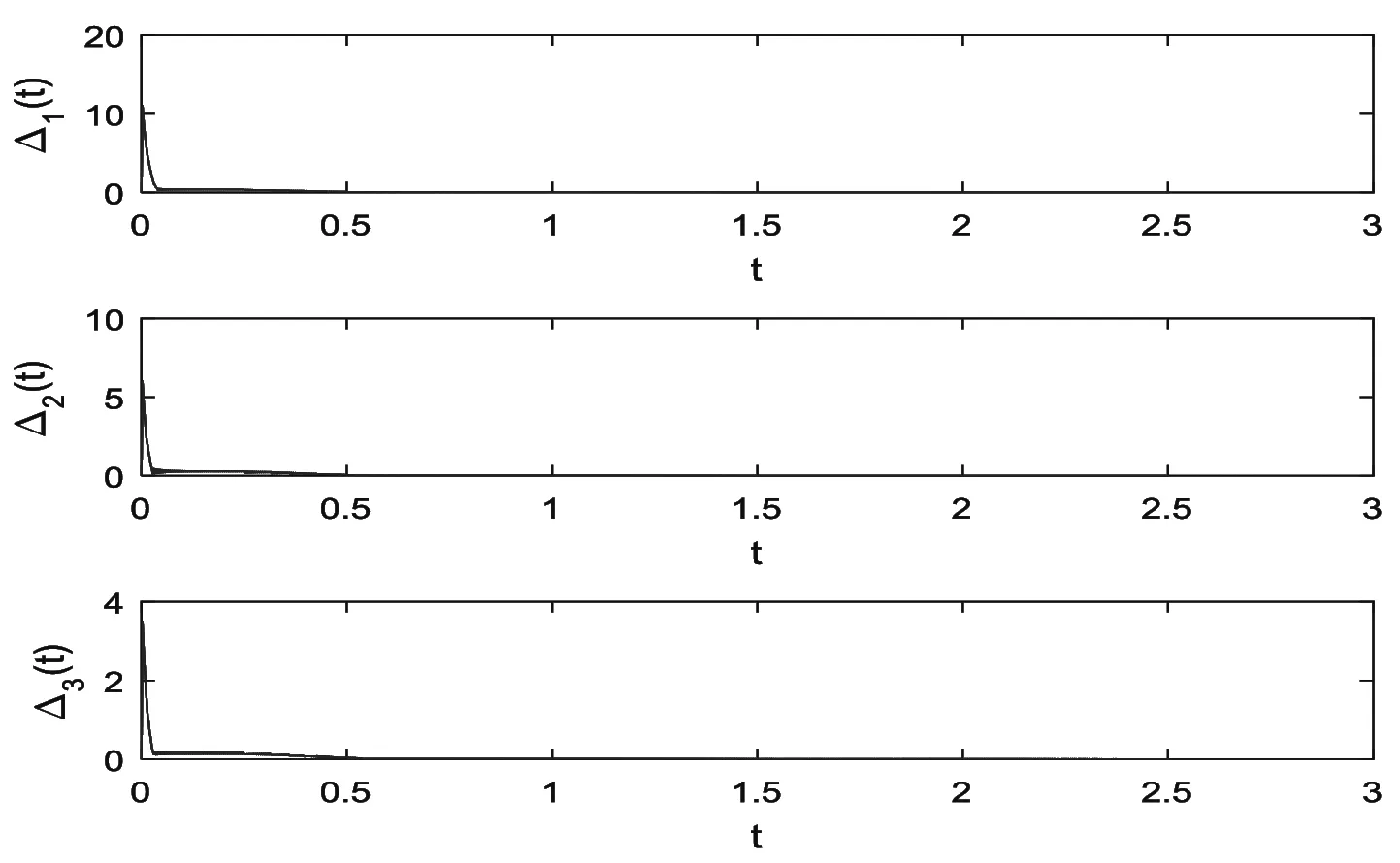
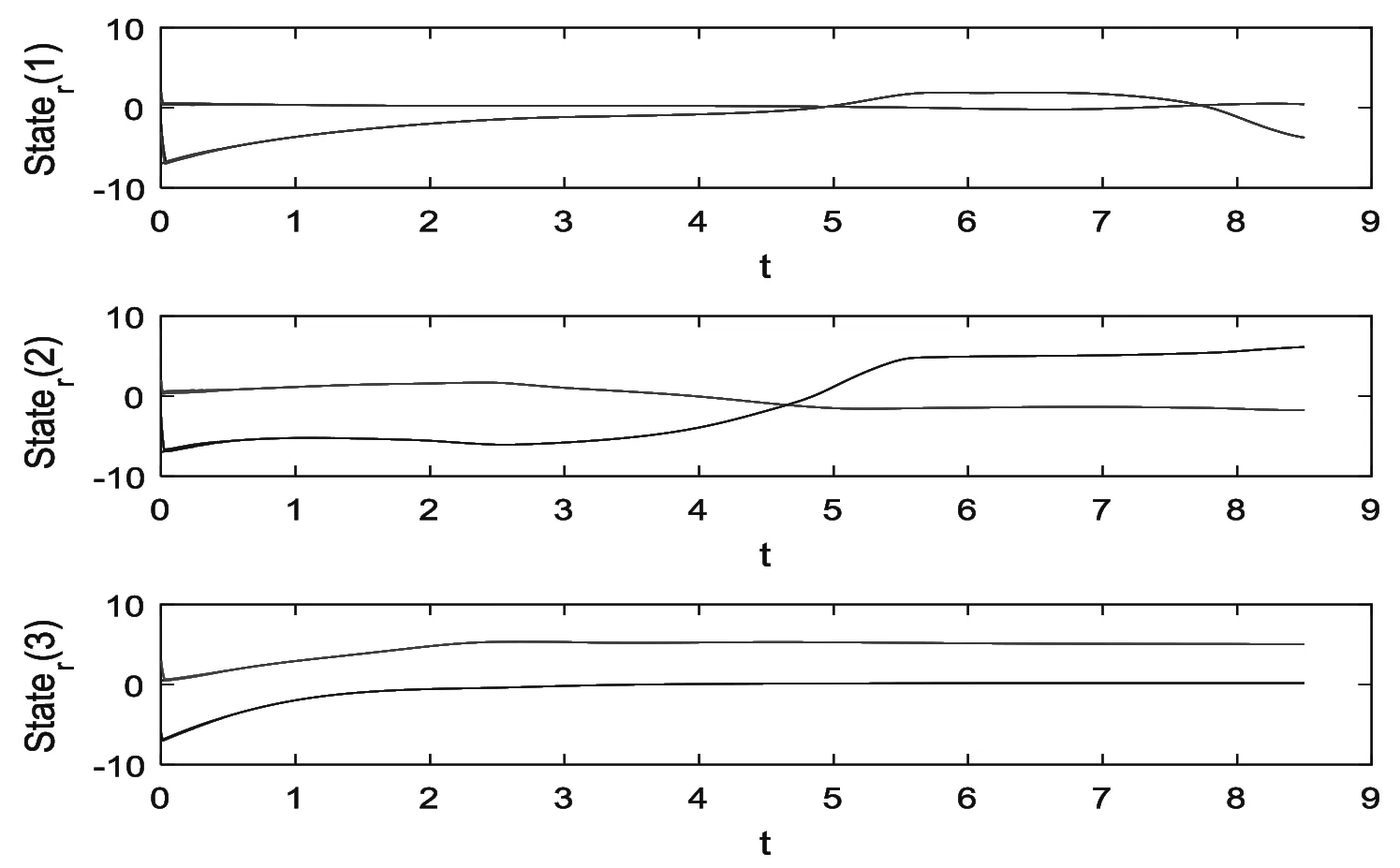
G=[gsj]N×N∈N×N的圖,這里的gsj滿足:對于任意的s=1,…,N有如果從第s個節點到第j個節點間有連接,則gsj>0,否則gsj=0.用{W1,W2,…,WM}表示具有M(2≤M 考慮由N個復值神經網絡構成的耦合系統,第s個復值神經網絡的動態方程可描述為: (1) 這里的zs(t)=(zs1(t),zs2(t),…,zsn(t))T∈n表示第s個復值神經網絡在t時刻的狀態向量; f(zs(t))=(f1(zs1(t)),f2(zs2(t)),…,fn(zsn(t)))T∶n→n表示神經元的激活函數;τ(t)是時變傳輸時滯且滿足n表示外部輸入;us(t)是被設計的控制器。 在本文中,我們假設(1)中的激活函數滿足如下所給假設條件: 假設2 令w=w1+iw2,其中w1,w2∈.fm(w)可由它的實部和虛部表示為: 基于以上假設,現令zs(t)=xs(t)+iys(t),其中xs(t),ys(t)∈n則復值神經網絡(1)可改寫為如下形式: (2) 將其寫成如下更緊湊的形式: (3) 這里 F1(ps(t))=((fR(xs(t)))T,(fR(xs(t)))T)T F2(ps(t))=((fI(ys(t)))T,(fI(ys(t)))T)T 系統(3)的初始條件如下: (4) 則復值神經網絡(1)能夠以有限時間t1實現集群{W1,W2,…,WM}的聚同步。這里的rk(t)表示第k個集群所有節點的相同局部動態。它可能是第k個集群中的平衡點,周期軌道或者是一個混沌吸引子,且滿足如下微分方程: (5) 類似地,把該復值神經網絡分解為實部和虛部,則(5)可改寫為如下形式: (6) 其中 假設3 假設耦合矩陣G滿足 其中Gkk∈(lk-lk-1)×(lk-lk-1)是一個具有非對角元素非負的零行和矩陣,Gkr∈(lk-lk-1)×(lr-lr-1)(k≠r)是零行和矩陣,k,r=1,2,…,M. 結合假設3和(5)式,對于任意的s∈Wk,k=1,2,…,M,有下式成立: (7) 在推導本文的結果前,先給出下面幾個非常有用的引理。 引理1[25]如果存在常數k1>k2>0,使得定義在[t0-τ,+∞)上的非負連續函數y(t)滿足如下不等式: h→0+表示h從右邊趨向于0. 引理2 假設V(t)是非負連續函數,如果 D+V(t)≤μ1V(t)+μ2?t≥t0 其中μ1≠0和μ2為常數,則對于任意的t≥t0,有下式成立: V(t)≤(V(t0)+μ2/μ1)eμ1(t-t0)-μ2/μ1 證明 在不等式D+V(t)≤μ1V(t)+μ2兩邊同乘e-μ1(t-t0),則有D+(e-μ1(t-t0)V(t))≤μ2e-μ1(t-t0),接著對該不等式左右兩邊從t0到t積分,即可得到V(t)≤(V(t0)+μ2/μ1)eμ1(t-t0)-μ2/μ1. 在這節中,給出了復值耦合神經網絡(1)漸近和有限時間聚同步的判據。 令es(t)=ps(t)-qk(t),s∈Wk,控制器設計如下: (8) 根據(3)(6)(7)和假設1,誤差動力系統可以描述為: (9) 基于以上準備,得到如下結果: (10) 構造如下非負函數 下面計算V(t)沿著系統(9)方向的右上Dini導數 (12) 這里的sgn(es(t))=(sgn(es1(t)),sgn(es2(t)),…,sgn(es,2n(t)))T∈2n, 顯然 (13) (14) 類似地,令 可以得到 (15) (16) 和 (17) 另一方面,有如下不等式成立 (18) 利用耦合矩陣G的性質,我們可以得到 和 然后結合(18)式可得如下不等式 (19) 接著,依次結合不等式(13)(14)(15)(16)和(17)得到不等式: ≤-aminV(t)+bmaxV(t-τ(t)) 這里的 定理證明完畢。 由于設計的控制規律us(t)是不連續的,因此系統(1)的解不能用常規意義下的解來定義。為了得到系統(1)的解,下面考慮Filippov意義下的解。 首先介紹關于集值映射的定義。對于任意的E?n,令 ER={Re(z)∶z∈E}EI={Im(z)∶z∈E} 假設E?n,稱z→F(z)是由E到n的集值映射,如果對任意z∈E,存在非空集合F(z)?n. 由文獻[23],我們可以定義系統(1)的Filippov解,如果z(t)在[t0,∞)的任意緊區間上絕對連續且滿足微分包含: (20) 則稱復值函數z(t)是系統(1)在[t0,∞)上滿足初值條件下的一個Filippov解,其中K[us(t)]表示us(t)的凸閉包。控制規律如下: (21) 令us(t)的集值映射為: 其中 將系統(1)分解為實部和虛部,則其微分包含可表示為 根據(5)(6)(7),假設1和微分包含原理,可得對于任意的t≥t0,誤差系統滿足下式 (22) (23) 另外可得 (24) (25) 最后將(23)式和(13)(14)(15)(19)和(25)式結合,有下面不等式成立 (26) 根據引理2,V(t)≤(V(t0)+)e-η(t-t0)-,這里的令 (27) 下證對于所有t≥T1,有V(t)=0成立。 作為定理2的一個特殊的情況,有如下結果成立: (28) 這節中,我們將給出幾個數值例子來闡述該文章的主要結果。 例1 考慮二維復值神經網絡(1),對于任意的zsj=xsj+iysj,其中xsj,ysj∈,激活函數滿足 對于任意的t∈[-1,0],rk=(0.5+0.8i,-2-3i)T,k=1,2,3.給定復值耦合神經網絡(1)的耦合矩陣如下 且系統(1)分為三個集群W1={1,2,3},W2={4,5},W3={6,7}.基于以上陳述,可得 (29) 通過計算可得: 這是一個非奇異M-矩陣。根據定理1,系統(1)在控制器(29)下能夠實現漸近聚同步。在模擬中,對于任意t∈[-1,0],令z1(t)=z4(t)=z6(t)=(0.5+0.8i,-2-3i)T,并且 zs(t)=(xs1+iys1,xs2+iys2)Ts=2,3,5,7 圖1 控制器(29)下的實部同步誤差軌跡 圖2 控制器(29)下的虛部同步誤差軌跡 由圖3和圖4也可看出所有狀態實現漸近聚同步。 圖3 控制器(29)下集群W1,W2,和W3的實部狀態圖 圖4 控制器(29)下集群W1,W2和W3的虛部狀態圖 (30) 并令 通過計算可得 根據定理2,系統(1)在控制器(30)下可以在有限時間實現聚同步,另外對于任意t∈[-1,0],令z1(t)=z4(t)=z6(t)=(0.5+0.8i,-7-8i)T,zs(t)的實部和虛部同例1是從[-10,10]中隨機產生的,其中s=2,3,5,7,于是可得這個同步時間估計值T1=16.8501.圖5和圖6可看出系統t≤2在同步,另外圖7和圖8也能明顯看出所有狀態在有限時間內實現了聚同步。這表明實際同步時間可能遠小于理論獲得值T1.這是因為定理2中T1是同步時間的上確界。因此找到有限時間同步更精確的上確界是一個值得探討的問題。 圖5 控制器(30)下的實部同步誤差軌跡 圖7 控制器(30)下集群W1,W2和W3的實部狀態圖 圖8 控制器(30)下集群W1,W2和W3的虛部狀態圖 本文主要討論了具有時變時滯的復值耦合神經網絡的漸近和有限時間聚同步的問題。在處理復值耦合神經網絡問題上采用實部虛部分離的方法。基于Halanay不等式理論得到了復值耦合神經網絡實現漸近聚同步的充分條件。基于Filippov解的框架和微分包含原理給出了復值耦合神經網絡在不連續控制規律下實現有限時間聚同步的準則,并推導出了同步時間的上確界。有限時間聚同步更精確的上確界是進一步可探討研究的問題。另外將漸近聚同步問題中的控制器設計為脈沖控制器或基于事件觸發的脈沖控制器也是我們下一步考慮研究的方向。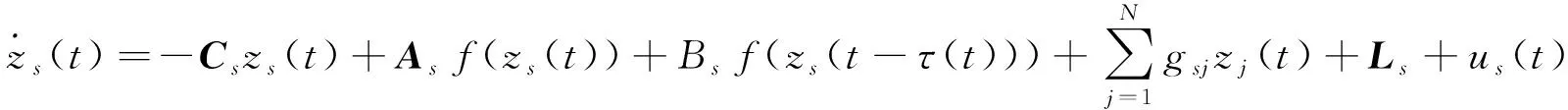
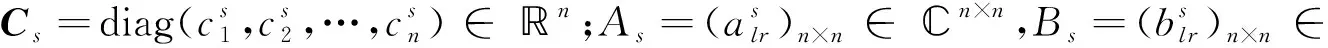
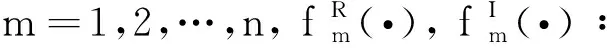
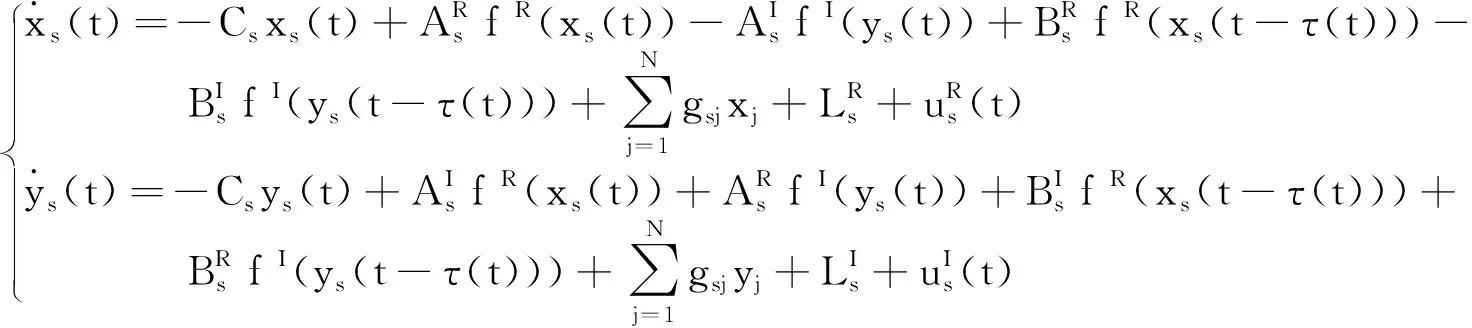
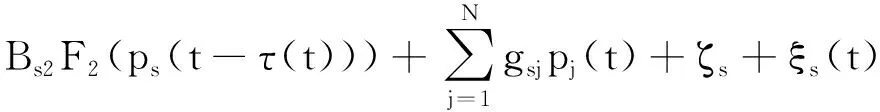
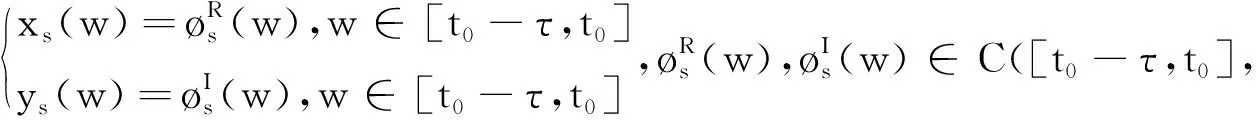
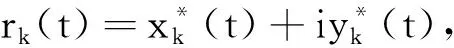
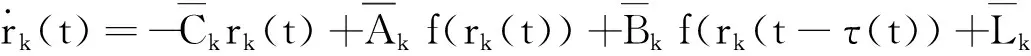
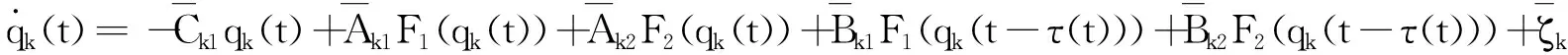
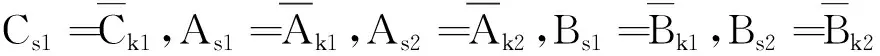

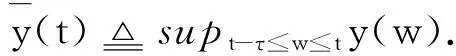
2 主要結果
2.1 漸近聚同步
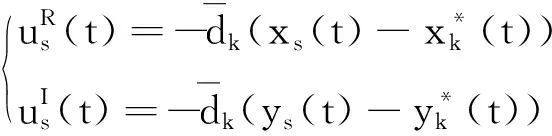
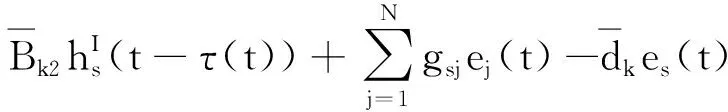
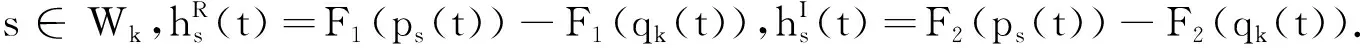
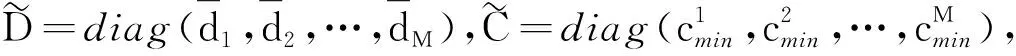
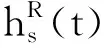
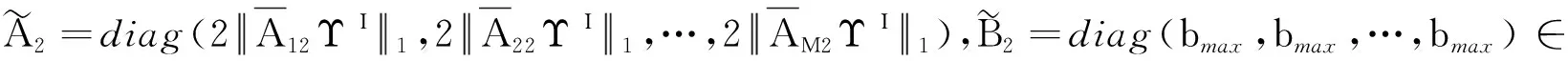
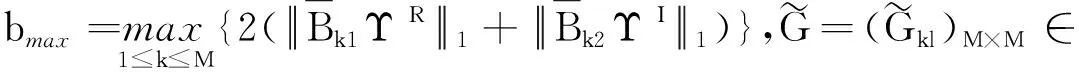
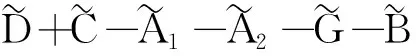
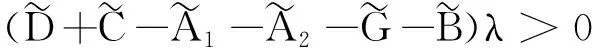
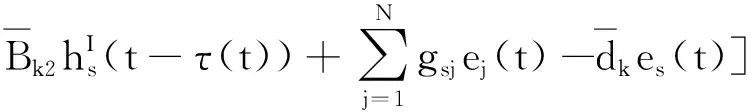
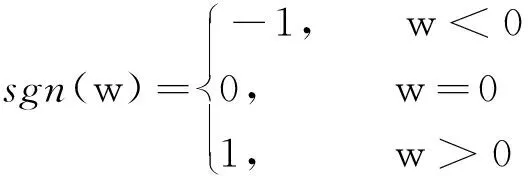
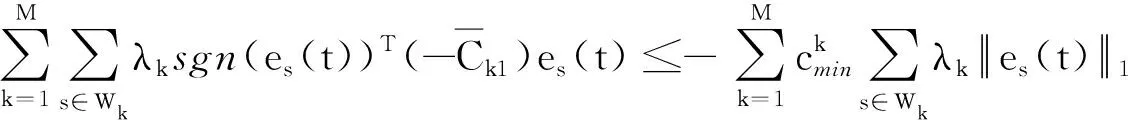
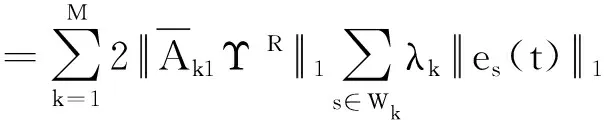
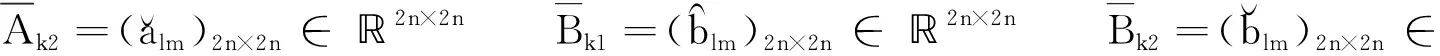
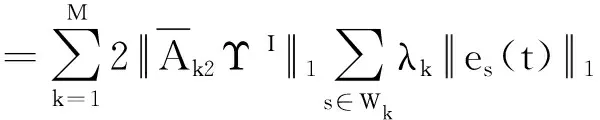
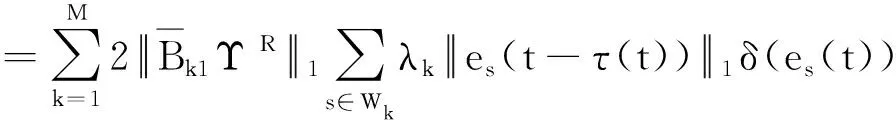
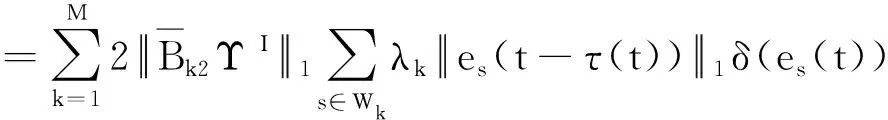

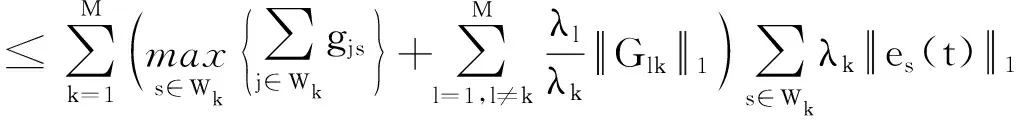
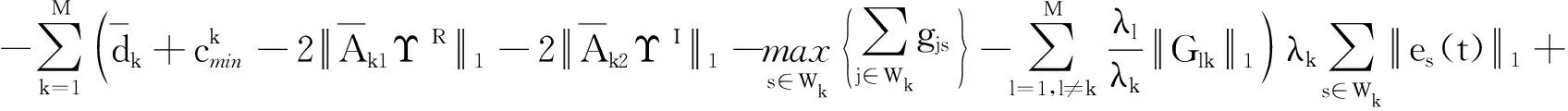
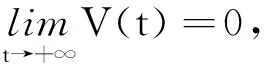
2.2 有限時間聚同步
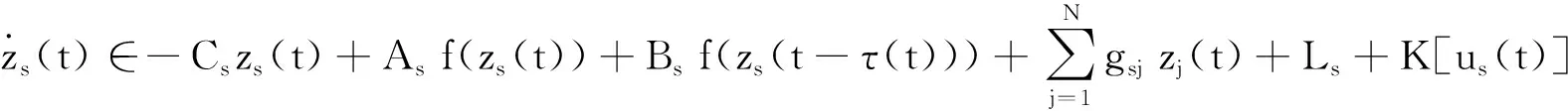
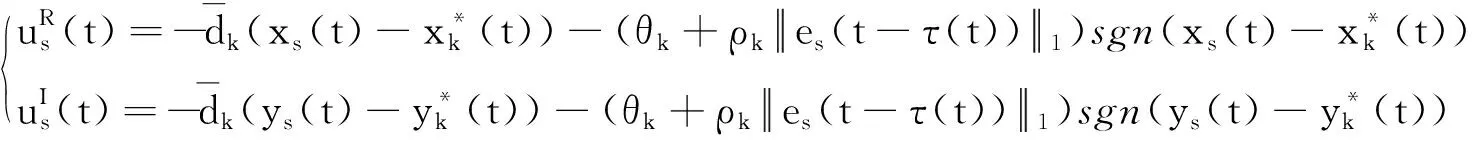
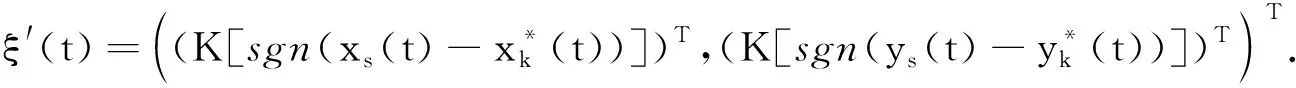
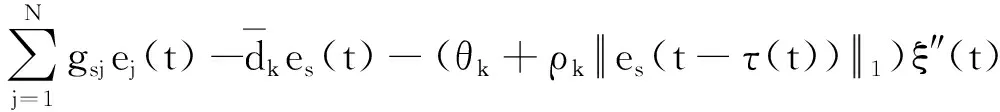
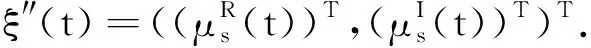
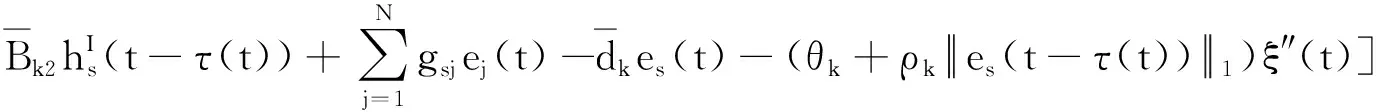
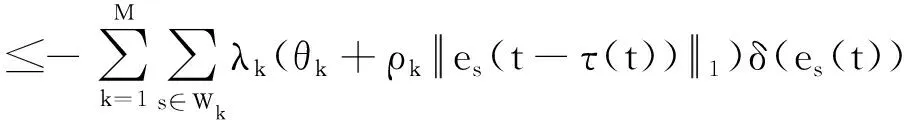
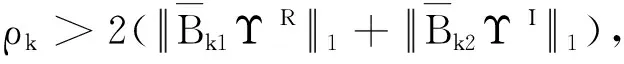
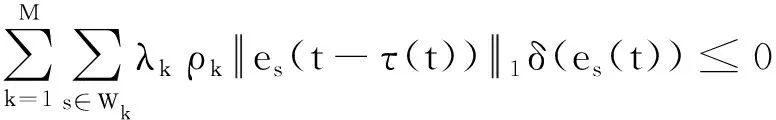
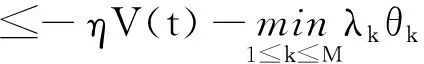
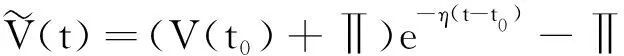

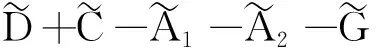
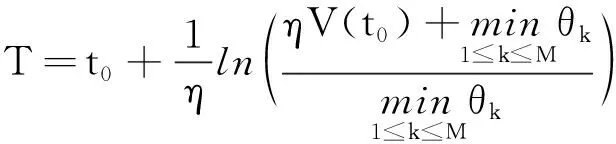
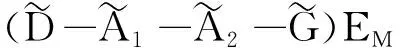
3 數值模擬
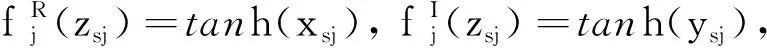

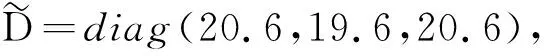
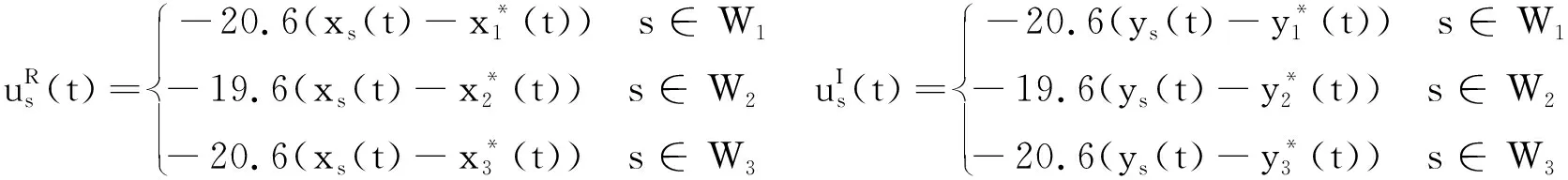
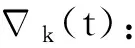
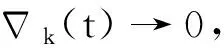
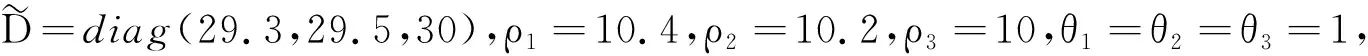
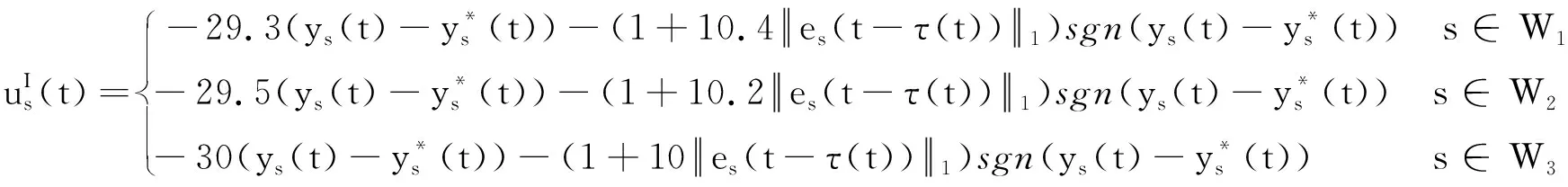
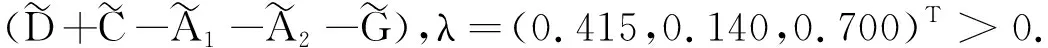
4 結論

