深海鉆井船大開口階梯形月池水體的非線性共振特性研究
石 城,呂海寧,楊建民
(1.上海交通大學海洋工程國家重點實驗室,上海200240;2.高新船舶與深海開發裝備協同創新中心,上海200240)
0 引 言
鉆井船對于海洋資源開發和海洋油氣開采有著重要作用。鉆井船的鉆井模塊為其開采的核心模塊,位于船中部,水下設備和鉆井設備通過船中部月池下放至水中。月池結構通常貫穿船體的甲板至船底,月池內的水體與外界水體連通,在外界波浪達到一定條件時,可能與月池內部水體產生共振現象。月池是鉆井船的核心結構之一,理想的設計可以在一定程度下屏蔽惡劣的外部環境。也有可能在某些條件下月池內部水體與外部波浪發生共振,損害船體結構、月池內部設備以及船上人員安全。
月池內部的水體運動主要為船長方向的晃蕩(sloshing)運動,以及垂向的升沉(heaving)運動。在實際情況中,兩種運動同時存在互相疊加,同時船身的運動、月池內部水體的運動以及環境波浪互相耦合。在階梯形的月池壁以及月池臺階處都有強烈的非線性特征,月池內部水體的多模態晃蕩使得月池水體水動力問題十分復雜。這些問題受到國內外學者的廣泛關注,許多問題仍有待解決。
可以看出,多數研究并沒有關注船體不同自由度對月池內部水體爬升的影響。本文采用數值模擬與模型試驗相結合的方法,研究了船體不同自由度對月池內水體爬升的影響,以及改變環境波高時,月池內部水體爬升幅值的響應情況。
1 數值計算
1.1 計算理論
對于非理想流體,其流場的控制方程包括連續性方程和動量方程,分別為
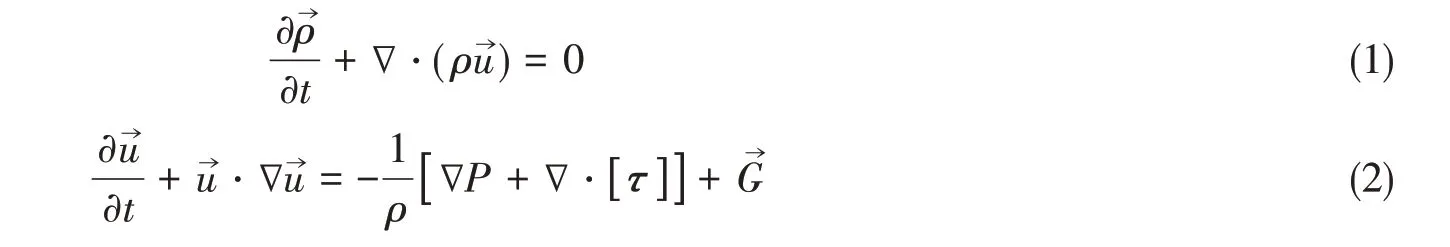
式中:t 為時間;ρ 為流體密度;u→為流體速度;G→為單位質量體積力,通常為重力加速度g;[ ]τ 為粘性應力張量。
本文數值模擬均為規則波,基于線性波浪理論中的Airy波理論和理想流體假設,二維速度勢為
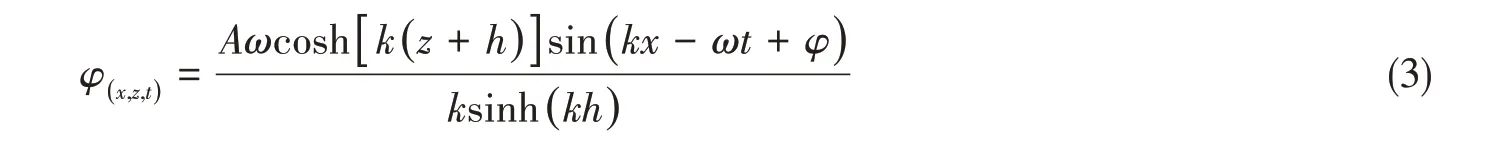
流體速度由以下兩部分分量組成:
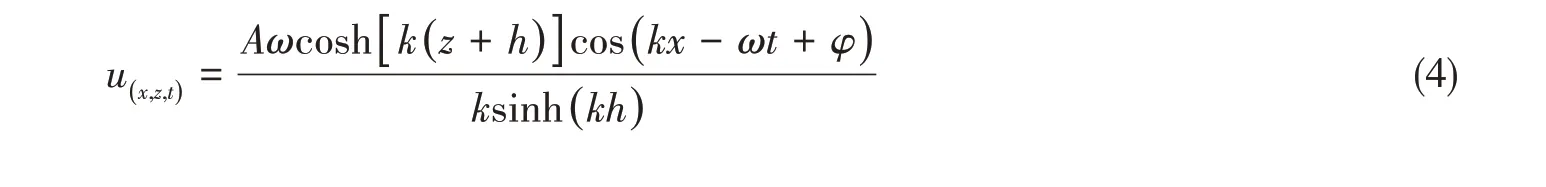
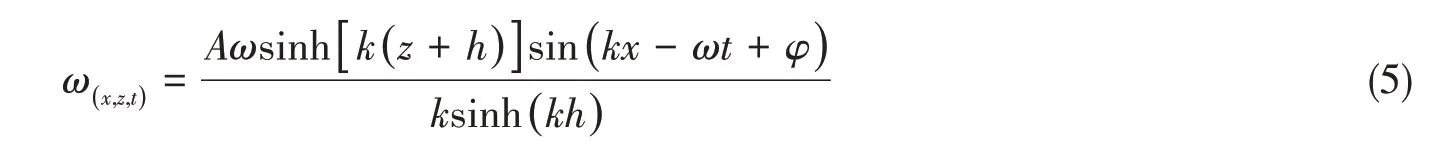
規則波的湍流模型采用SST k-w湍流模型,表達式為

式中,F1為混合函數,其計算公式為
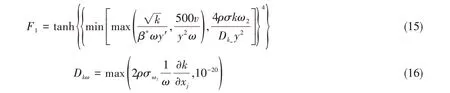
本文所使用的自由液面模擬方法為VOF 法,基本原理為定義一個流體域體積函數F 來追蹤自由液面的變化,函數F 表示網格單元內流體體積占該單元總體體積的比值。若F=0,表明這是一個空單元,內部無流體;若F=1,表明該單元全部被流體所充滿;F在0到1之間,表明該單元部分被流體充滿,或者這種單元含有自由邊界。除了F值介于0到1之間,還需要相鄰單元中至少有一個是F=0的空單元。F的控制微分方程為

自由液面的法線方向可由F 的梯度來決定,得出各單元的F 值及其梯度之后,就可確定自由液面的位置和形狀。
船體運動只考慮剛體運動。運動學上,剛體的任何運動都可以分解為一個平動加一個轉動,剛體上任何一點的速度都可以表示為一個選定基點的速度加上這一點關于這個基點的轉動速度,通常選擇剛體的重心作為基點,剛體運動可表示為


1.2 數值水池建立與網格劃分
數值模擬中,模型縮尺比為1∶50,在外部軟件Rhino 中建立(如圖1 所示)。選擇計算流體力學Star-ccm+軟件建立數值水池并進行數值計算。數值水池尾端設有消波區,水池入口端距船尾兩倍船長,水池出口端距船尾三倍船長(如圖2所示)。求解器采用隱式求解器,隱式求解器可以加強流體與船體運動之間耦合運動的計算,保證計算準確性。

圖1 帶月池鉆井船模型Fig.1 Drilling vessel model

圖2 數值水池及網格劃分Fig.2 Numerical wave tank and meshing model
本文采用重疊網格進行數值模擬,網格總量為640萬個。對自由液面垂向及縱向均進行網格細化,數值模擬保證在每個波高內有超過25 個網格,在每個波長內有超過160 個網格。計算時間步長Δt=0.04 s,船體網格劃分及距數值水池入口處1 m 的波形如圖3所示,波浪在數值水池內可以保證無衰傳播。經過驗證確定,目前的計算精度與計算速度可以得到較好的兼顧。
在數值模擬中,船體自由度分成三種不同情況。Case 1:船體靜止;Case 2:船體有垂蕩運動;Case 3:船體有垂蕩及縱搖運動。本文還對比三種環境波高作用時,月池內部水體爬升情況。具體工況如表1所示。

表1 數值模擬工況Tab.1 Numerical circumstances
2 模型試驗
本試驗的模型縮尺比為λ=1∶50,模型按照縮尺比進行制作。在模型試驗中,首先采用不同頻率環境波浪進行試驗,并根據月池內部水體響應情況確定船體共振頻率。后續試驗采用的環境波浪頻率均為此共振頻率,監測月池內部自由液面升高情況。本試驗在上海交通大學海洋深水試驗池進行。
2.1 鉆井船模型
本次試驗研究的鉆井船船長約為180 m,船中有矩形大開口帶階梯月池,模型試驗情況如圖4 所示。為了防止模型在波浪作用下產生橫蕩或縱蕩等位移,試驗過程對鉆井船進行水平系泊。試驗內容包括靜水衰減試驗、白噪聲試驗和規則波試驗。模型試驗中的鉆井船模型與實船參數及模型試驗照片如表2和圖4所示。

表2 船體及月池參數Tab.2 Geometric parameters of ship and moonpool

圖4 鉆井船模型試驗Fig.4 Model experiment
在模型試驗中對月池內部A、C、F 三處進行波浪爬升監測。坐標原點取在船尾處,各個監測點的坐標和位置如表3及圖5所示(A與F并非月池最前端和最后端),模型試驗系泊情況如圖6所示。

表3 各監測點坐標值Tab.3 Coordinates of monitoring points
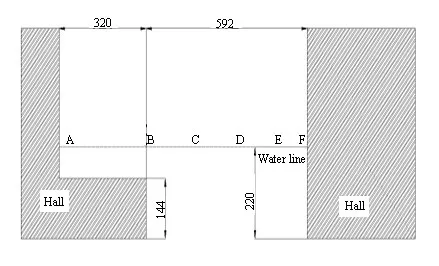
圖5 月池內部監測點位置示意圖Fig.5 Monitoring points
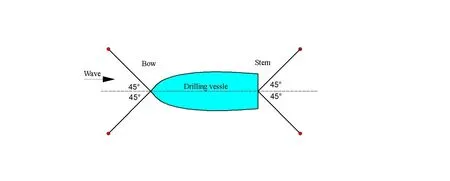
圖6 模型試驗水平系泊示意圖Fig.6 Horizontal mooring method
2.2 波浪頻率選定
本次模型試驗首先采用不同頻率的環境波浪進行模型試驗,通過觀測月池前后端的監測點C 處及F 處的自由液體面爬升情況,不同頻率下監測點波浪爬升情況如圖7 所示,最終得出模型試驗的共振頻率f'=0.92 Hz。考慮到模型試驗中船體仍然存在除縱搖和垂蕩外的其他自由度的微幅運動(數值計算中不存在),故本文基于船體最多僅有垂蕩和縱搖兩個自由度的情況,進行數值模擬,計算得到共振頻率f=0.87 Hz,f 與f'相差甚小,對月池內水體爬升影響甚微。本文數值計算中的環境波浪頻率均取此共振頻率。
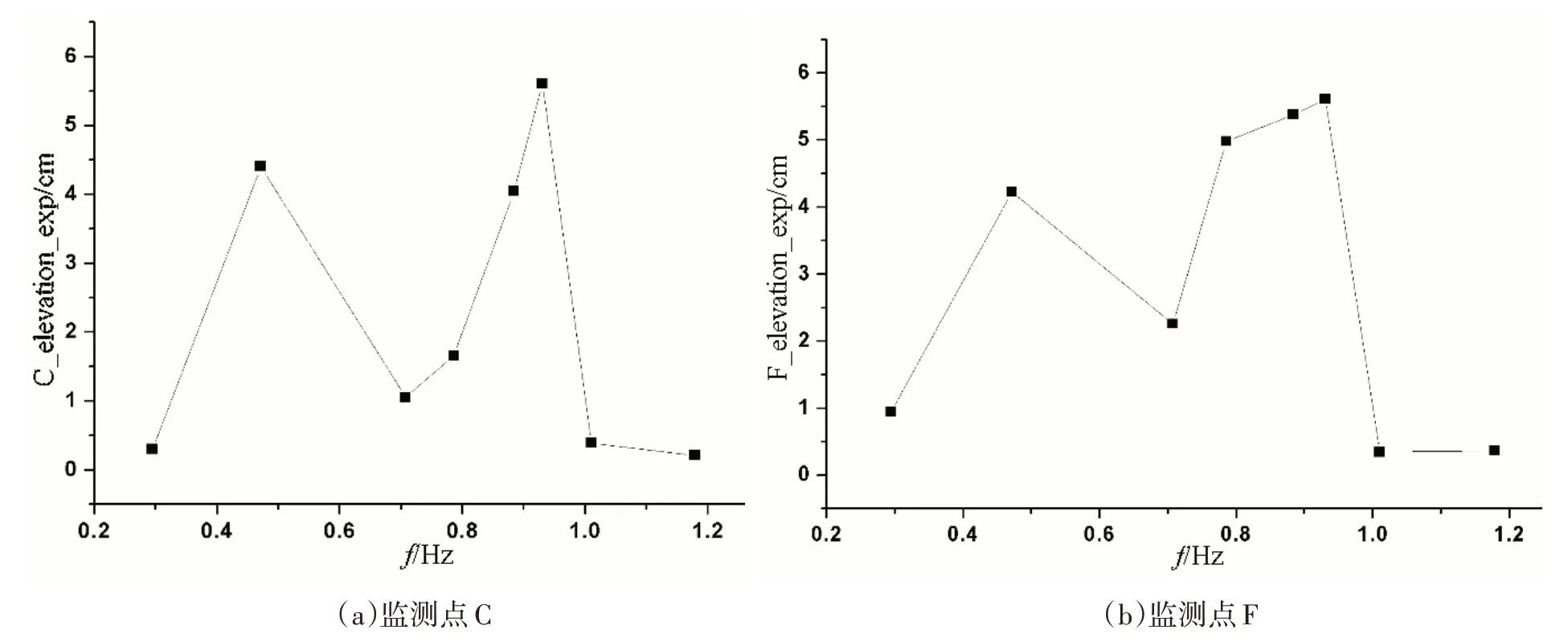
圖7 不同波浪頻率下的水體波高Fig.7 Wave elevations under different wave frequencies
3 計算結果與分析
3.1 數值模擬與模型試驗結果對比
對比月池兩個端點A、F處模型試驗及數值計算結果(見圖8),模型試驗情況下的內部水體爬升幅值略高于數值計算結果(如圖8 所示)。盡管模型試驗時對船體進行了水平系泊,船體其他自由度的運動仍然無法避免,結果存在微小偏差,說明數值模擬與模型試驗結果吻合較好。
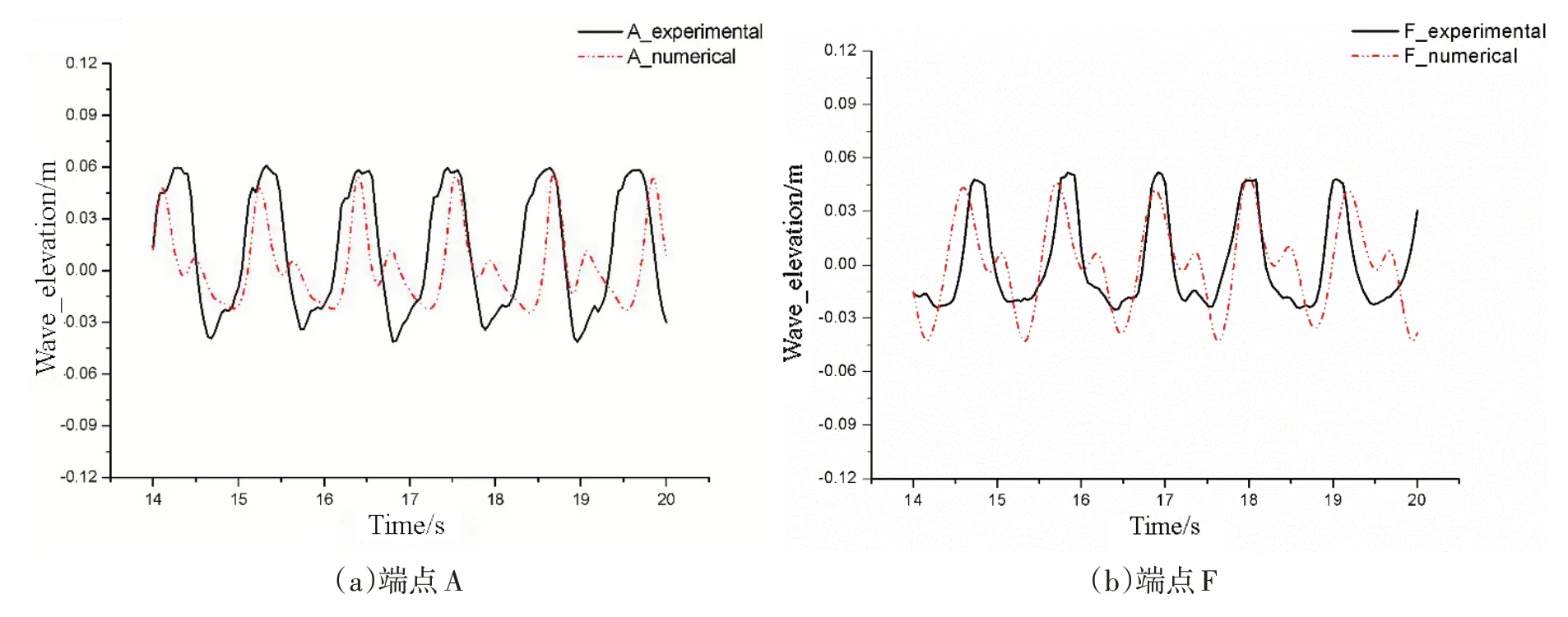
圖8 A和F處數值結果與試驗結果對比Fig.8 Numerical and experimental results at monitoring points of A and F
3.2 船體不同自由度運動對月池內部水體爬升的影響
3.2.1 船體垂蕩運動對月池內部水體爬升的影響
為了探究船體垂蕩運動對月池內部水體爬升產生的影響,分別對船體靜止(static)以及船體僅具有垂蕩自由度(heaving)時進行數值模擬。環境波高h=0.04 m,月池內各處水體爬升情況如圖9所示。
由圖9 可見,船體具有垂蕩自由度時(Case 2),月池內部的波浪爬升幅值遠高于在船體靜止時(Case 1)的爬升幅值。船體垂蕩自由度可以對月池內部水體爬升幅值產生激勵作用,在研究月池共振問題時,船體運動不可忽略。
3.2.2 船體縱搖運動對月池內部水體爬升的影響
為了探究船體縱搖運動對月池內部水體爬升的影響,對船體釋放垂蕩及縱搖自由度(Case 3)進行數值模擬,環境波高仍為h=0.04 m,與船體僅具有垂蕩運動(Case 2)的模擬結果進行對比。結果如圖10所示。
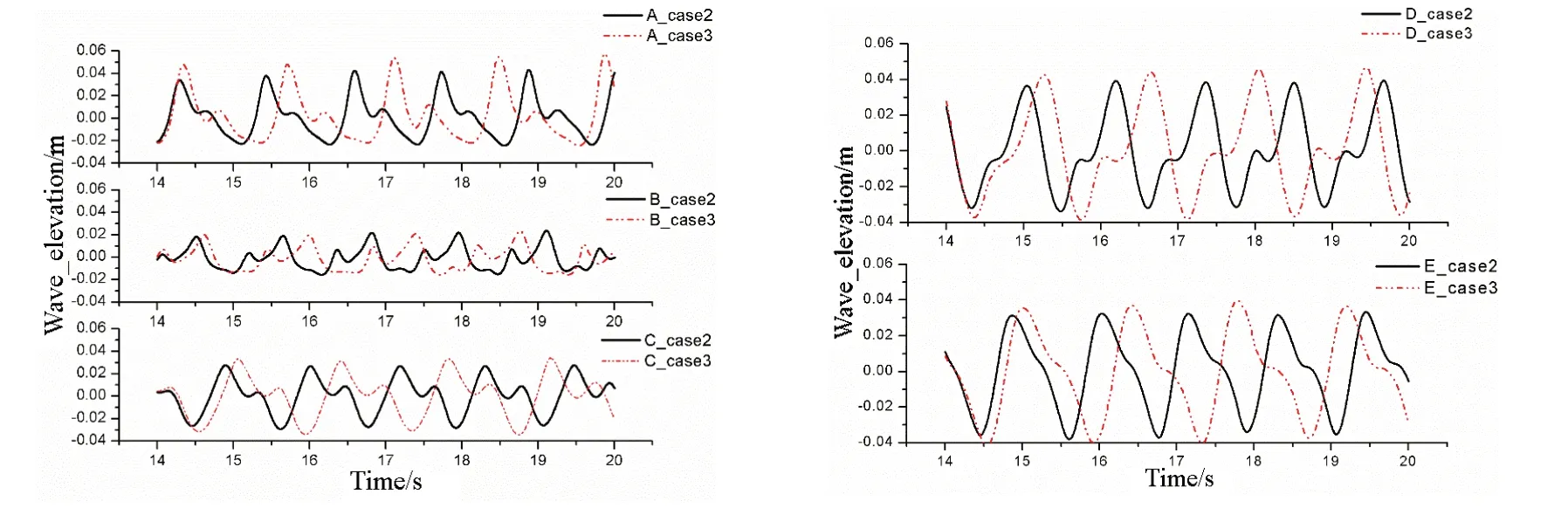
圖10 Case2及Case3時各處水體爬升對比Fig.10 Wave elevations under Case2 and Case3
對比Case 2與Case 3月池內部A-E處的自由液面升高情況,可以發現,A處水體爬升幅值在Case 3時相對于Case 2 有大幅提升,其他監測點處自由液面爬升幅值也有小幅增加。船體縱搖運動會對月池內部水體晃蕩幅值產生放大,由于淺水效應,A 處水體爬升幅值增幅較大。同一監測點在Case 2 與Case 3兩種情況下月池內水體晃蕩周期不同,船體縱搖運動會對月池內部水體晃蕩周期產生影響。
3.3 波高對月池內部水體爬升的影響
本文探究環境波高對月池內部水體爬升的影響,增加環境波高至h=0.06m和0.08 m。月池內部各監測點水體爬升情況如圖11和圖12所示。
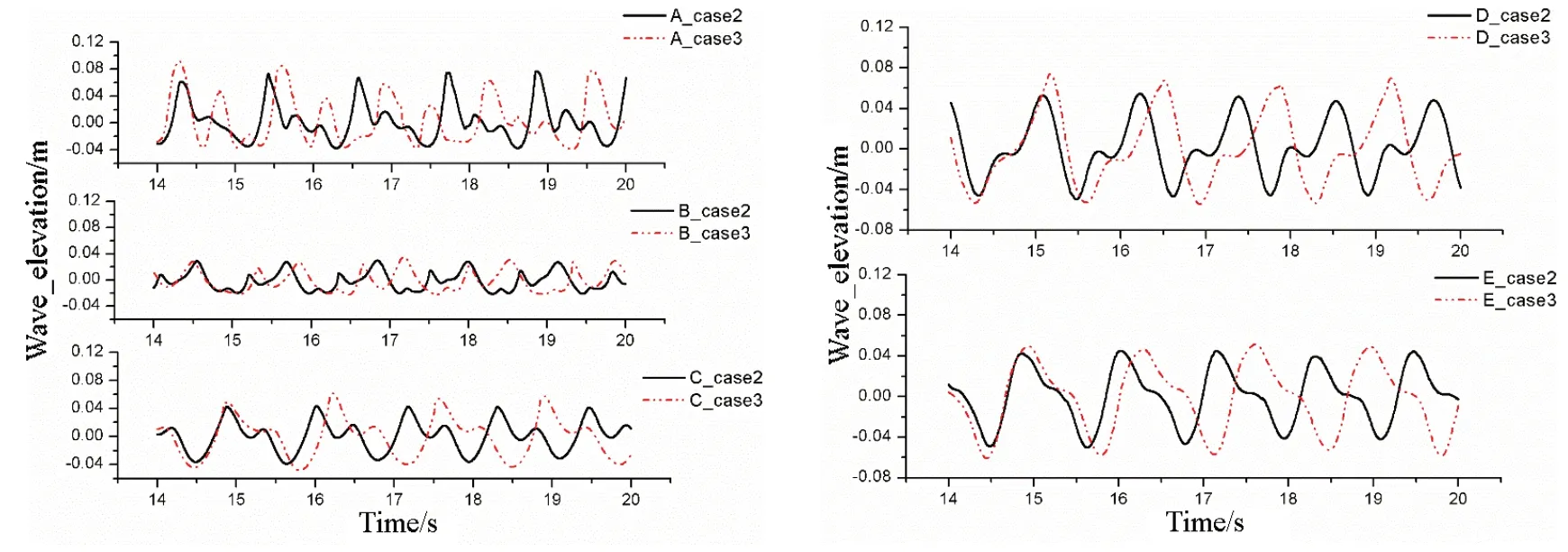
圖11 波高h=0.06 m,Case 2及Case 3時各處水體爬升對比Fig.11 Wave elevations under Case 2 and Case 3 at a wave height of 0.06 m
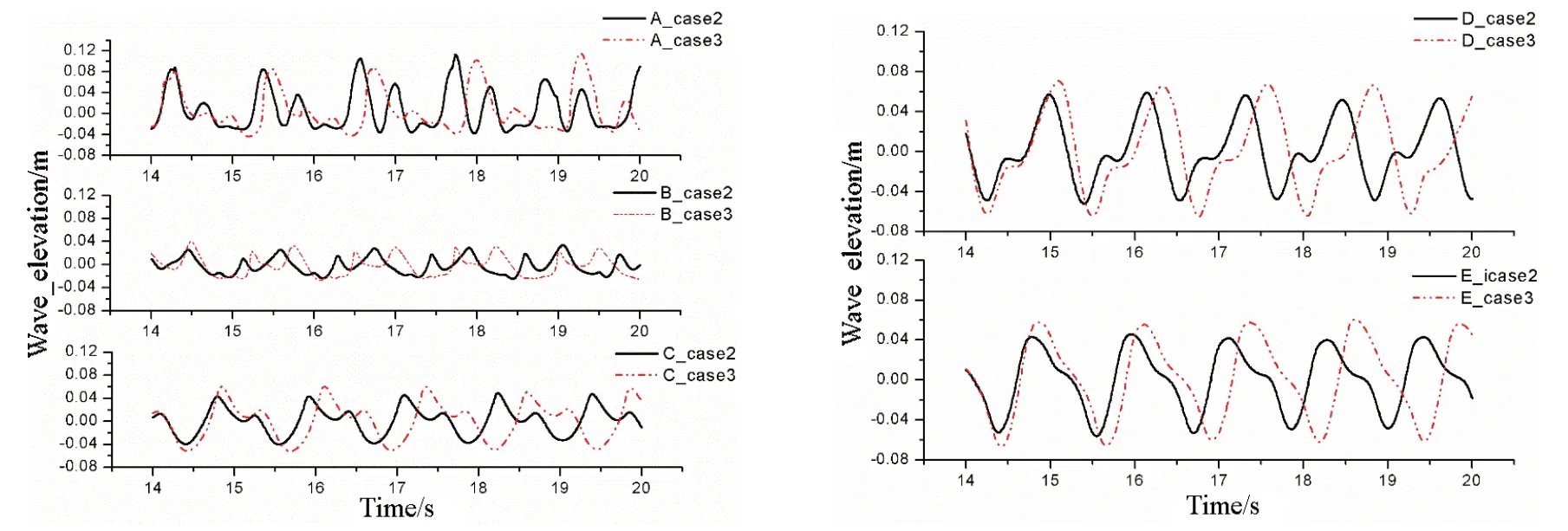
圖12 波高h=0.08 m,Case 2及Case 3時各處水體爬升對比Fig.12 Wave elevations under Case 2 and Case 3 at a wave height of 0.08 m
分析A、B 處波浪爬升幅值,自由液面經歷一次峰值后,隨即又經歷了一次幅值較低的二次爬升。這種二次爬升現象在A、B 處明顯,且環境波高增加時二次爬升幅值增加。在Case 3 情況下波浪的二次爬升幅值明顯高于Case 2 時的幅值。二次爬升現象源于月池內部水體的多模態晃蕩,是強非線性的體現,且船體縱搖會增加各階晃蕩的幅值。
月池問題的強非線性使得月池內部水體多模態晃蕩問題較為復雜。為探究月池內部水體晃蕩各模態對應的頻率及幅值情況,本文對波高h=0.08 m,船體具有垂蕩及縱搖運動時(Case 3)的數值結果進行頻域分析,結果如圖13所示。
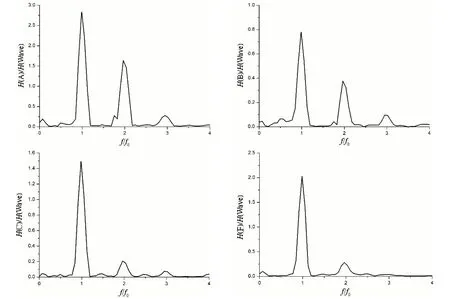
圖13 A、B、C、F處頻域分析Fig.13 Analysis of frequency domains at monitoring points of A,B,C and F
經過四點處的頻域分析可以發現,各處均存在不同幅值的晃蕩模態。主共振頻率為f0=0.87 Hz,與試驗測量值吻合,波浪頻率為2f0及3f0時,月池內部產生高階爬升現象。A 處的水體主模態爬升幅值以及其他模態爬升幅值均高于其他位置,B 處水體的各階模態爬升幅值均小于波幅,這是由月池的后端(A處)淺水效應及月池邊界的強非線性所引起的。
統計A-E 各監測點在環境波高不同、船體運動自由度不同情況下波浪爬升高幅值,結果如圖14所示。
由圖14 可知,當環境波高由h=0.04 m 上升至h=0.06 m 時,A 處自由液面爬升幅值由0.045 m 增加至0.09 m,達到了之前的約2 倍;波高繼續增加至0.08 m時,A 處波浪爬升幅值達到0.12 m。環境波高由0.04 m 上升至0.06 m 時,C、D、E 處的自由液面爬升幅值均有小幅增加;波高達到0.08 m 時,C、D、E 處波浪幅值變化很小。月池內水體運動有強烈的非線性,這使得在環境波高線性增加時,內部水體響應并非線性,而是幅值增量趨緩。
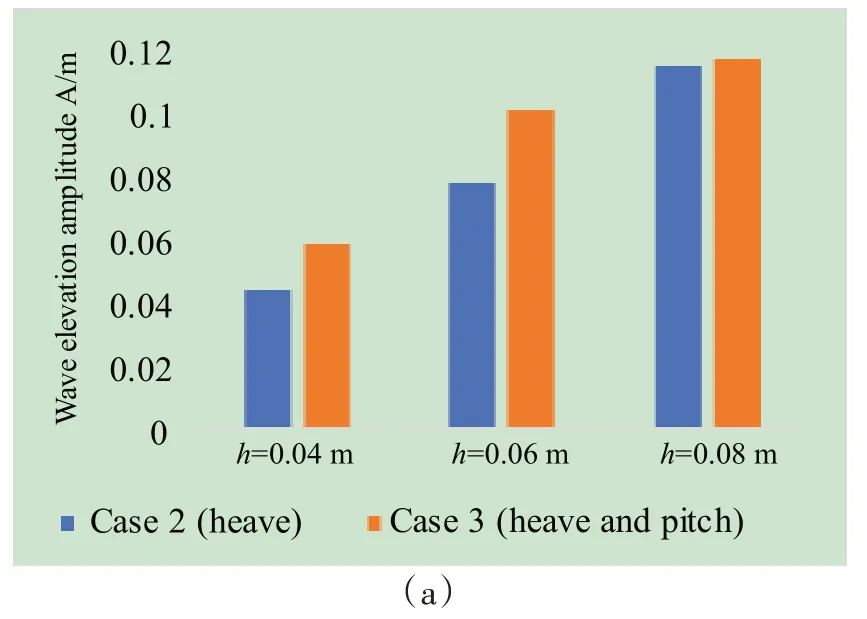
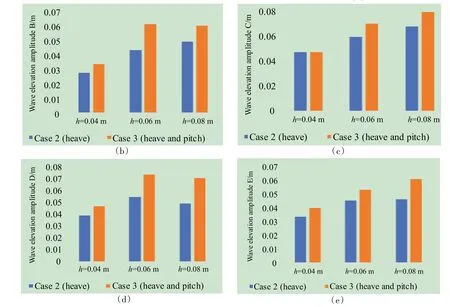
圖14 不同船體自由度、不同波高時,月池內A-E處自由液面幅值統計Fig.14 Statistics of wave elevations under different ship motions and different outside wave heights
4 結 論
本文通過改變船體運動自由度以及環境波浪波高,對月池內部水體爬升進行了探究,并將對應數值結果與模型試驗結果進行了對比,驗證了數值模擬的準確性,得到了以下結論:
(1)月池會對外部水體產生屏蔽作用,月池內部水體滯后于外界波浪;
(2)船體垂蕩、縱搖運動都會使月池內部水體爬升幅值增加,由于月池壁處的淺水效應,月池后端(A處)爬升幅值增量最大,研究月池共振問題時船體運動不可忽略;
(3)船體縱搖運動與環境波浪發生耦合,會影響月池內部水體的二次爬升幅值,也會影響內部水體晃蕩周期;
(4)月池內部水體運動具有強非線性,水體存在多模態晃蕩運動;
(5)由于月池內部水體的強非線性,環境波浪波高線性增加時,內部水體爬升幅值并非線性響應,而是幅值增量趨緩。

