兩種典型立柱截面浮式平臺渦激運動耦合特征試驗研究

魏東澤，闕小玲，楊晨斌，白興蘭

（浙江海洋大學a.海洋工程裝備學院；b.船舶與海運學院，浙江舟山316022）

0 引 言

浮式平臺的渦激運動會加重立管、錨泊系統的疲勞損傷，降低使用壽命，因此一經發現就成為了海洋工程界的研究熱點之一。目前深水海洋平臺，如半潛式平臺及TLP平臺，其立柱截面形狀主要以圓形和方形為主，國內外已有諸多學者[1-6]針對不同立柱截面形狀的海洋結構物VIM問題進行了研究，但大多將研究重點集中在橫蕩及縱蕩兩個自由度上。隨著研究的深入，學者們發現在一定的來流條件下平臺會發生較為劇烈的艏搖運動：Goncalves 等[7-9]針對帶圓形倒角的方形立柱半潛式平臺的VIM問題進行了一系列的試驗研究，探討了各個流向下艏搖運動的響應幅值與約化速度的關系，并指出在進行半潛式平臺設計時不應忽略艏搖運動的影響；Liu[10]等采用模型試驗的方法對方形立柱半潛式平臺的渦激運動問題進行了研究，以艏搖運動為重點探討來流方向和縱橫比對平臺VIM特征的影響，從各個流向下橫蕩運動以及0°流向下艏搖運動觀察到了“渦激共振”現象；Gu[11]等對深吃水變截面立柱的新型FDPSO 進行了數值模擬研究，分析了其橫蕩、縱蕩及艏搖運動情況，并將模型試驗結果與數值模擬結果進行了對比驗證，結果表明，新型FDPSO 的渦激運動特征與傳統FPSO 有所不同，45°流向下艏搖運動響應幅值遠大于0°流向情況，并且艏搖運動頻率主峰值接近平臺固有頻率；Kim[12]等采用DDES-SST 模型對八立柱結構型式的半潛式平臺VIM 問題進行了數值模擬研究，并將所得結果與模型試驗結果進行了對比，發現在橫蕩、縱蕩及艏搖的響應頻率和響應幅值方面均擬合良好，其研究結果為半潛式平臺的VIM預測提供了一種實用方法。

目前學者們對于浮式平臺艏搖問題的研究主要集中于流向角、縱橫比等因素對于艏搖運動響應幅值的影響。本文對兩種典型立柱截面的海洋浮式平臺在不同流向下的渦激運動問題進行了試驗研究，并以艏搖運動為重點，分析來流方向和立柱截面形狀對平臺三自由度運動響應幅值的影響，并探討了在渦激運動的不同階段中，艏搖運動與橫蕩、縱蕩運動的耦合關系。

1 模型試驗方案

1.1 模型介紹與試驗方案

本試驗模型為典型四立柱結構，由有機玻璃制成，平臺立柱有圓柱和方柱兩種，圓柱平臺（circu?lar cross-section platform ，簡寫為CCP）和方柱平臺（square cross-section platform，簡寫為SCP）幾何尺寸如表1 所示。試驗水槽長30 m、寬1 m、深1 m，水槽邊壁距離兩平臺立柱外緣分別為40 cm 和38 cm，均大于6 倍立柱特征長度，因此邊壁效應基本可以忽略。試驗采用循環式潛水泵造流系統造流，最大造流能力可達0.8 m/s。本試驗設計了一種由四組彈性系泊纜組成的等效系泊方案，分別將模型底部、模型上部與固定用鐵環相連，以模擬平臺在真實工作環境下的水平、垂直系纜剛度。在前后立柱中上部及平臺底部質心處分別安裝加速度傳感器，采用DASP多功能數據采集分析系統對加速度信號進行采集，通過對加速度數據進行二次積分處理獲得平臺橫蕩、縱蕩及艏搖響應時程曲線。試驗裝置如圖1所示。

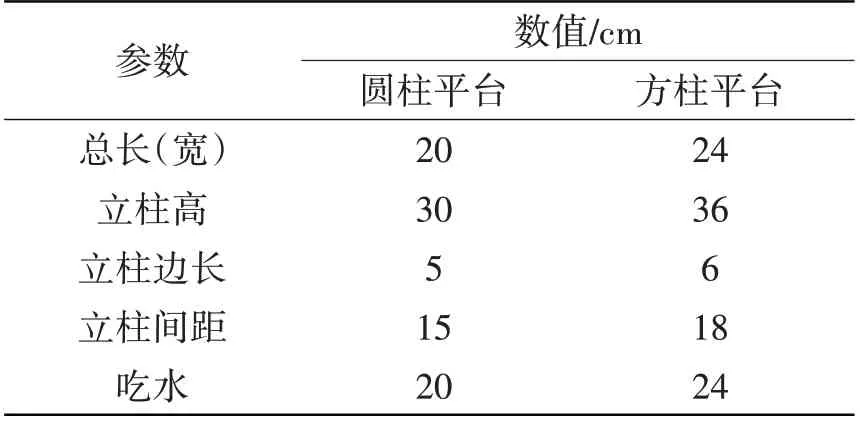
表1 兩平臺模型參數Tab.1 Main parameters of the platforms

圖1 平臺模型Fig.1 Platform models

1.2 自由衰減試驗

為了獲取平臺各自由度的固有頻率，首先進行了自由衰減試驗。試驗流速范圍為0.06～0.50 m/s，共16 個流速工況。通常情況下，海洋工程結構鎖定現象發生的約化速度范圍約為4～11，16 個試驗工況對應約化速度應盡量大于此范圍。通過調整系纜剛度可以改變系統固有頻率，從而達到使約化速度范圍滿足試驗需要的目的。對橫蕩、縱蕩及艏搖自由衰減時程曲線進行傅里葉變換，所得結果如圖2 所示，可得fc-sway=fc-surge=0.67 Hz、fc-yaw=1.58 Hz，fs-sway=fs-surge=0.54 Hz、fs-yaw=1.28 Hz，其中，下標c 表示圓柱平臺，下標s 表示方柱平臺。可以計算出對應的約化速度范圍分別為：圓柱1.79～14.93、方柱1.85～15.43，包括了通常情況下的鎖定區及鎖定區前、后足夠寬闊的約化速度范圍，使試驗結果能更好地反映平臺運動的運動規律。

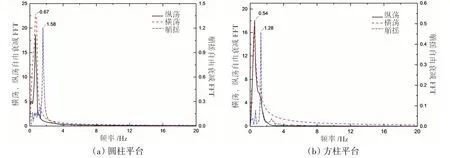
圖2 兩平臺自由衰減FFT曲線Fig.2 Free attenuation curve after the Fourier transform of two platforms

采用約化速度反映流速對平臺渦激運動特征的影響，約化速度表達式如下：

為分析艏搖固有頻率對平臺渦激運動特征的影響，定義Ury為采用艏搖固有頻率表達的約化速度，即

計算得對應的Ury范圍為：圓柱0.76～6.33，方柱0.78～6.51。式中，U為試驗流速，D為特征長度。

2 試驗結果與數據分析

2.1 運動響應幅值分析

圖3 給出了圓柱和方柱平臺在來流方向分別為0°和45°時橫蕩運動響應幅值隨約化速度變化情況。由圖可見，兩流向下的圓柱平臺以及45°流向下方柱平臺的橫蕩運動在約化速度約為5～12 的范圍內都發生了較為明顯的“渦激共振”現象，而0°流向下方柱平臺的橫蕩運動響應幅值則始終保持隨約化速度的增大而增大的趨勢。在絕大多數工況下，圓柱平臺的橫蕩運動幅值均明顯大于方柱平臺，兩者相差最大可達6.1倍，但是在流向角為45°時，圓柱和方柱的橫蕩運動幅值比較接近，當約化速度超過12后，方柱平臺的橫蕩運動幅值甚至超過了圓柱平臺。

圖4給出了圓柱和方柱平臺在來流方向分別為0°和45°時縱蕩運動響應隨約化速度的變化情況。由圖可見，圓柱平臺的縱蕩運動在約化速度大約4～8范圍內發生了小幅的“渦激共振”現象，但幅值增大并不明顯。總的來說，兩流向下，兩平臺的縱蕩運動響應幅值基本保持隨約化速度增大而增大的趨勢。相同流向下，在整個約化速度范圍內，兩平臺縱蕩運動幅值較為接近，但前者始終稍大于后者，其中圓柱平臺縱蕩運動最大幅值為0.33D，方柱平臺為0.24D。

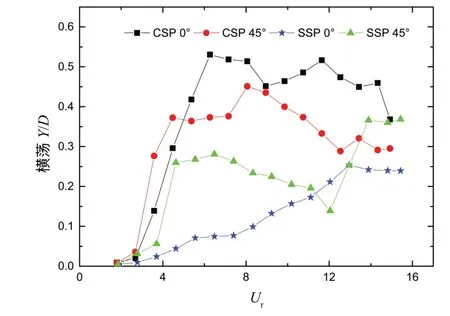
圖3 不同流向下兩平臺橫蕩響應幅值Fig. 3 Transverse responsive amplitude of two platforms at different current headings

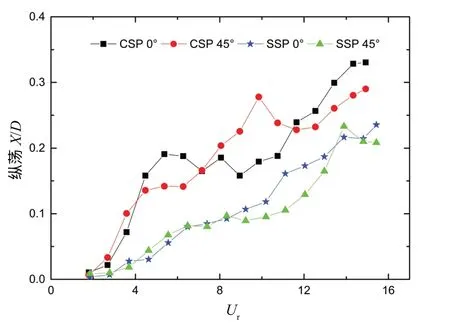
圖4 不同流向下兩平臺縱蕩響應幅值Fig.4 Inline responsive amplitude of two platforms at different current headings

圖5 給出了圓柱和方柱平臺在來流方向分別為0°和45°時艏搖運動響應隨約化速度的變化情況以及與Goncalves 經典試驗所得結果的對比情況,圖中底部橫坐標為約化速度Ur，頂部橫坐標為采用艏搖固有頻率表示的約化速度Ury。由圖可見，本試驗所得圓柱平臺的艏搖運動響應幅值大小以及隨約化速度變化規律與Goncalves試驗結果十分接近，說明了本文模型及試驗方案的可靠性。此外，本文所得艏搖響應幅值與Goncalves 經典試驗結果也有一些不同之處。首先，在Goncalves 試驗中，各個流向下的艏搖運動響應幅值在通常情況下鎖定區范圍內（約化速度約為4～10）均沒有觀察到“渦激共振”現象，而在0°流向下，Ury在4～8范圍內，平臺艏搖運動發生了明顯的渦激共振現象，體現了艏搖固有頻率對平臺渦激運動特征的影響。本試驗中，在45°流向下，約化速度約為4～11 范圍內，從方柱平臺的艏搖運動觀察到了明顯的渦激共振現象，這說明在特定流向下艏搖運動也可能發生渦激共振。因此，在進行平臺、立管等結構的設計時，應考慮大幅艏搖運動問題。當Ury≥4 時，圓柱平臺、方柱平臺的艏搖運動響應幅值出現了大幅增大的現象，究其原因，應為此時艏搖運動頻率（fc-yaw≥1.24 Hz，fs-yaw≥0.93 Hz）分別與各自艏搖固有頻率接近，而使艏搖運動發生共振現象，同樣體現了艏搖固有頻率對平臺VIM特征的影響。其次，相同工況下本試驗中方柱平臺獲得的艏搖運動響應幅值遠大于Goncalves 試驗結果，本試驗中45°流向下共振區的方柱艏搖運動最大幅值可達20°左右，而Goncalves 試驗中，兩流向下平臺最大艏搖響應幅值僅為5°左右。造成這一差異的原因可能是平臺模型的立柱截面形狀不同：Goncalves試驗采用模型的立柱截面形狀為帶圓形倒角的正方形，而本試驗方柱平臺模型截面形狀為正方形，沒有倒角，渦街脫落形態、分離點位置都有所不同；另外，兩試驗模型浮箱結構型式以及浮箱高度與平臺吃水的比值有所不同，也可能對平臺的艏搖運動產生了一定影響。

2.2 三自由度運動耦合特征分析

圖6給出了0°流向下，圓柱和方柱平臺的橫蕩、縱蕩和艏搖三自由度運動響應頻率主峰值隨約化速度的變化情況。由圖可見，兩平臺三自由度運動頻率主峰值隨約化速度變化規律比較類似，大致都可以分為3個階段。第一階段中，渦激運動尚未發生，此時平臺各自由度運動的主峰頻率值基本耦合于平臺的固有頻率。第二階段包括了渦激運動的非鎖定區及鎖定區，在這個階段中，兩平臺的三自由度響應頻率具有相似的耦合關系：橫蕩、縱蕩及艏搖響應頻率主峰值基本保持1∶1∶1 關系，說明此時三自由度運動耦合程度較高。兩平臺的橫蕩響應均只有唯一峰值頻率，兩平臺的艏搖響應頻率均出現了與主峰頻率成2倍、3倍關系的次峰頻率，如圖7（a）、（b）所示；圓柱平臺的縱蕩響應由于受到艏搖運動影響，出現了次峰頻率，并且耦合于艏搖運動的2倍關系峰值頻率，如圖7（a）所示；方柱平臺的縱蕩響應只有唯一峰值頻率，如圖7（b）所示。第三階段為渦激運動的超鎖定區階段。在這個階段中，平臺三自由度運動的耦合關系比較復雜：圓柱平臺的橫蕩、艏搖運動響應頻率主峰值隨約化速度的增加進一步增大，并基本保持1∶1.5 關系，如圖8（a）所示，方柱平臺的橫蕩、艏搖響應頻率主峰值同樣隨約化速度的增加進一步增大并繼續保持1∶1關系，如圖8（b）所示。兩平臺縱蕩頻率均出現降低，并基本穩定于0.38 Hz 附近，不再隨約化速度的增加發生明顯變化，結合2.1 節對于響應幅值的分析可以推定，此約化速度范圍內兩平臺的縱蕩運動發生了高幅值、低頻率的“馳振”現象。另外，圓柱平臺的縱蕩運動出現了耦合于艏搖運動主峰頻率的次峰頻率值，說明兩者具有較強的耦合關系。

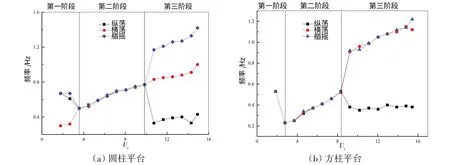
圖6 0°流向下兩平臺運動頻率Fig.6 Motion frequencies of two platforms at 0°incidence

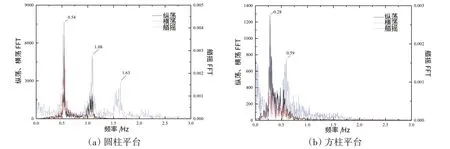
圖7 0°流向下第二階段兩平臺渦激運動頻率耦合關系Fig.7 Frequency coupling feature of VIM of two platforms in the second stage at 0°incidence

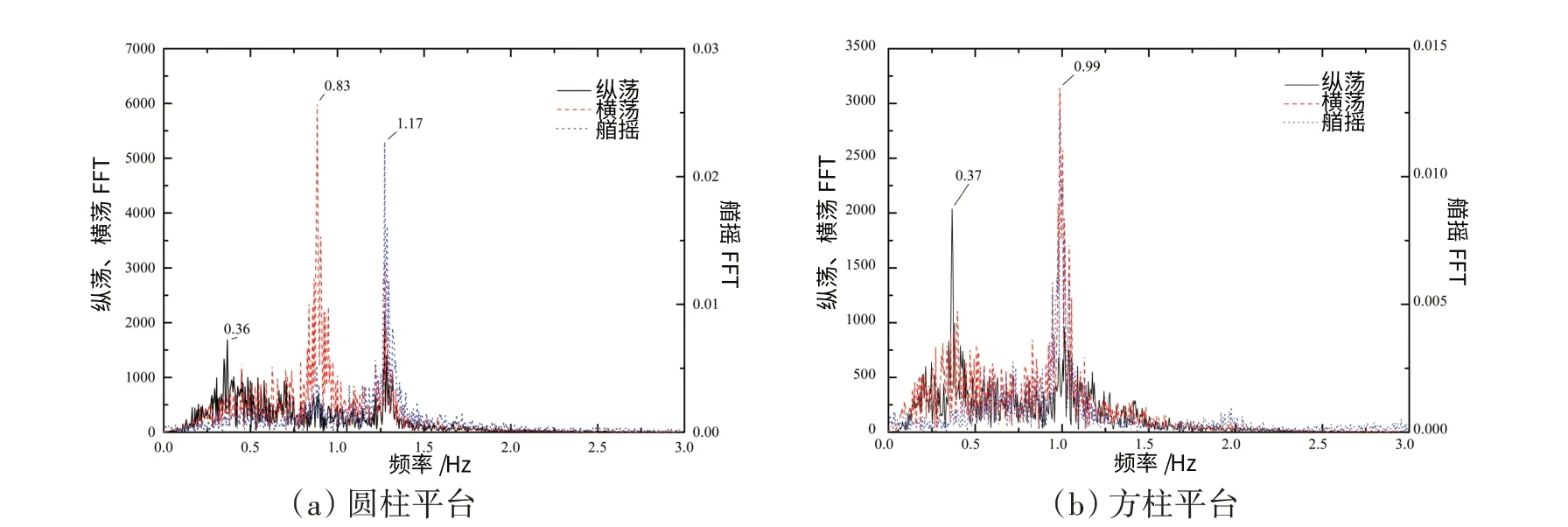
圖8 0°流向時第三階段中兩平臺渦激運動頻率耦合關系Fig.8 Frequency coupling feature of VIM of two platforms in the third stage at 0°incidence

圖9給出了45°流向下，圓柱和方柱平臺的三自由度運動頻率主峰值隨約化速度的變化情況。由圖可見，兩平臺三自由度運動頻率主峰值隨約化速度變化大致也可以分為3個階段。第一階段中，兩平臺三自由度運動頻率基本耦合于平臺固有頻率，而第二、第三階段中，兩平臺三自由度運動耦合關系差別較大。第二階段中，圓柱平臺三向運動耦合關系與0°流向第二階段基本相同，此處不再贅述。第二階段方柱平臺的艏搖運動觀察到了特殊的“主頻跳動”現象：在此階段中艏搖運動出現兩個明顯的峰值頻率，數值上與橫蕩運動頻率成1倍和2倍關系，不同約化速度下，這兩個峰值頻率交替成為艏搖運動的主峰值。例如，當約化速度為4.63 時，艏搖運動頻率主峰值為0.46 Hz，與橫蕩運動頻率成1∶1 關系，2 倍頻峰值0.92 Hz 為其次峰值，如圖10（a）所示；而當約化速度為5.56 時，艏搖運動響應頻率主峰值為0.97 Hz，與橫蕩響應頻率成2∶1關系，而1倍頻峰值0.49 Hz為其次峰值，如圖10（b）所示。此現象說明當流向角為45°時，邊界層的渦旋脫落方向具有一定的隨機性，導致鎖定區域內平臺的艏搖與橫蕩運動頻率比例關系具有一定的不確定性。

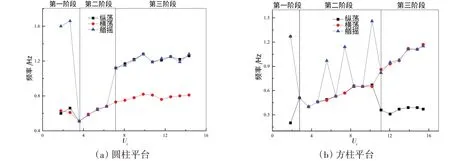
圖9 45°流向下兩平臺運動頻率Fig.9 Motion frequencies of two platforms at 45°incidence

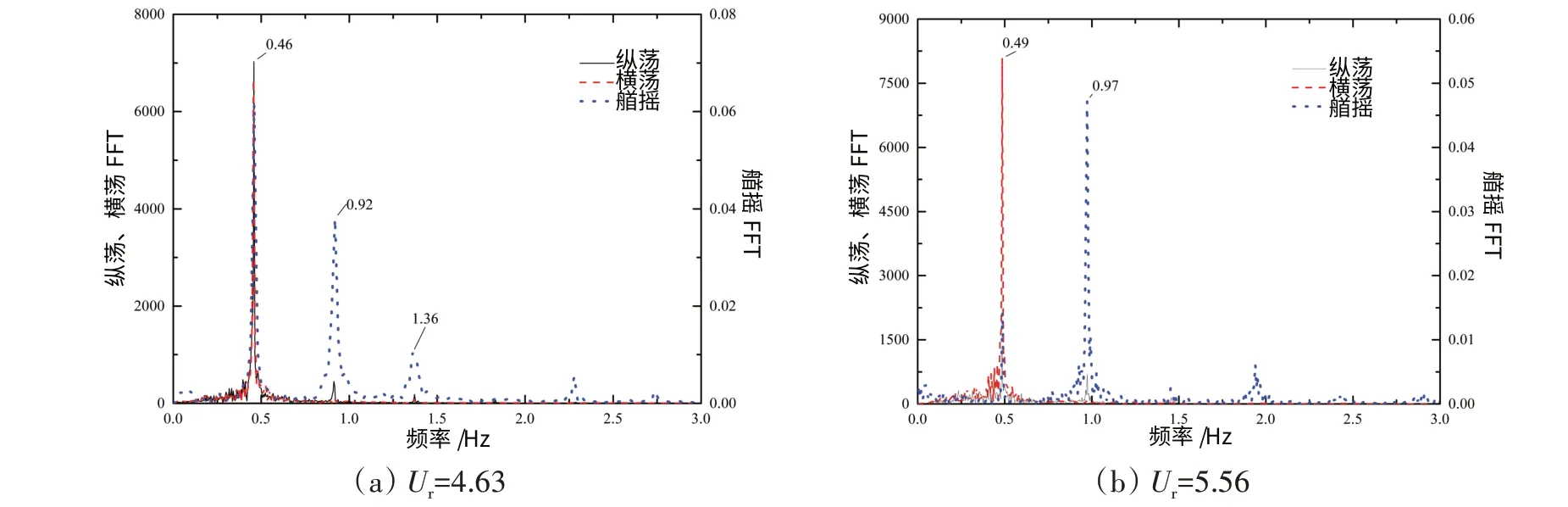
圖10 45°流向下方柱平臺第二階段渦激運動頻率耦合關系Fig.10 Frequency coupling feature of VIM of SCP in the second stage at 45°incidence

第三階段中，圓柱平臺橫蕩的運動頻率隨約化速度的增加逐漸增大，縱蕩和艏搖運動在進入第三階段后頻率主峰值出現突增并始終保持基本相同，說明在此階段縱蕩運動與艏搖運動具有較高的耦合性。整個第三階段中橫蕩、縱蕩、艏搖基本保持1∶1.5∶1.5 的關系，如圖11 所示。方柱平臺在第三階段中三自由度運動耦合關系與0°流向時基本相同，縱蕩運動也觀察到了“馳振”現象。

圖11 45°流向時第三階段圓柱平臺渦激運動頻率耦合關系Fig.11 Frequency coupling feature of VIM of CCP in the third stage at 45°incidence

3 結 論

本文針對兩種典型立柱截面形狀的浮式平臺在不同來流方向下的渦激運動問題進行了試驗研究，以艏搖運動為重點，探討了平臺VIM 響應幅值隨約化速度的變化情況，以及渦激運動的不同階段內平臺三自由度運動耦合關系，得到以下結論：

（1）圓柱平臺在不同流向下的橫蕩運動均觀察到明顯的“渦激共振”現象，方柱平臺的橫蕩運動是否發生共振還與來流方向有關。大多數工況下，圓柱平臺的橫蕩響應幅值明顯大于方柱平臺，兩者最大相差6.1倍。

（2）圓柱平臺的艏搖運動響應幅值隨約化速度變化情況與Goncalves 經典試驗結果基本一致。45°流向下方柱平臺艏搖運動在約化速度為4～11 的范圍內發生了明顯的“渦激共振”現象，這與Gon?calves 試驗結果有明顯的不同，說明在一定條件下，艏搖運動發生共振現象的可能性不應該被忽略。在Ury≥4 時，由于艏搖運動頻率與艏搖固有頻率接近，同樣可能引起艏搖運動發生渦激共振現象。另外，相同工況下，本試驗中方柱平臺艏搖運動響應幅值遠大于Goncalves 試驗結果，可能與倒角的抑振作用、浮箱結構以及平臺吃水等因素有關。

（3）立柱截面形狀和來流方向會對浮式平臺的渦激運動響應和耦合特征產生明顯影響，但呈現出一些基本規律。0°和45°流向下，整個約化速度范圍內圓柱和方柱平臺三自由度運動耦合關系大致都可以分為3 個階段：第一階段中平臺三自由度運動頻率基本耦合于平臺固有頻率；第二階段中，平臺三自由度運動頻率主峰值基本保持1∶1∶1關系，說明此階段中平臺VIM 具有較高的耦合性；第三階段中，兩平臺的運動耦合關系較為復雜，兩流向下方柱平臺的縱蕩運動均觀察到“馳振”現象，橫蕩與艏搖運動頻率主峰值基本保持1∶1 關系；0°流向下的圓柱平臺縱蕩運動也觀察到了“馳振”現象，橫蕩與艏搖運動頻率主峰值變為1∶1.5關系，45°流向下圓柱平臺的橫蕩、縱蕩及艏搖運動頻率主峰值比例關系為1∶1.5∶1.5，這說明在VIM 的超鎖定區，方柱平臺的艏搖運動與橫蕩保持較高的耦合性，而圓柱平臺的艏搖運動與縱蕩運動的耦合性更高，也說明“馳振”現象是否發生與立柱截面形狀、來流方向等因素關系密切。