基于動力學模型分塊逼近的水下機械臂RBF滑模控制算法研究

趙 偉， 張曉暉， 楊松楠

(西安理工大學 自動化與信息工程學院， 陜西 西安 710048)

多關節機械臂由于其靈活性，是執行水下資源勘測、水下檢測維修等任務的理想工具。區別于陸用機械臂，水下機械臂在運動時會受到水作用力的影響以及多種難以預測的外部干擾[1]。分析水下機械臂的受力情況與提高水下機械臂的控制精度有助于水下機械臂的設計研發[2]。

精準的動力學模型是水下機械臂運動仿真與控制器設計的基礎[3]。文獻[4]通過理論分析計算了單關節水下機械臂的動力學模型。文獻[5]利用Navier-Stokes方程計算了物體在水中的動力學模型，該方法求解過程復雜，不適用于多關節水下機械臂。文獻[6]使用切片理論計算了水下機械臂的動力學模型，提供了新的計算思路。文獻[7]使用微分變化法構建了機械臂在水環境中的動力學模型，通過仿真驗證了機械臂在靜水環境中受水作用力的影響，但沒有計算水流對機械臂的沖擊力。

實時性和抗干擾性是衡量水下機械臂控制器性能的重要指標[8]。水下機械臂是典型的多輸入多輸出的非線性系統，國內外研究學者針對此類系統提出了許多先進控制算法。文獻[9]將前饋模糊補償器引入滑模控制算法，用于消除動力學模型中的不確定干擾項。文獻[10]使用自適應滑模控制算法實現了水下機械臂的控制，該算法具有良好的魯棒性，但實時性仍有待提高。文獻[11]和文獻[12]利用徑向基(RBF)網絡動態逼近模型誤差，提高了多關節機械臂控制器的響應速度，證明了利用前饋神經網絡在多關節機械臂控制器設計中的有效性。

本文利用切片理論與Morison公式計算了雙關節水下機械臂在運動時受到的水阻力、附加質量力、浮力與水流的沖擊力，結合傳統機械臂動力學方程推導出雙關節水下機械臂在水環境中的動力學模型。基于動力學模型提出了一種RBF滑模控制策略，該策略使用多個RBF神經網絡分塊逼近動力學模型中的不確定項，快速補償計算模型與實際模型的誤差；使用飽和函數改進控制律，削弱控制系統的抖振效應。

1 水下機械臂動力學建模

1.1 傳統機械臂動力學建模

雙關節水下機械臂的結構簡化示意圖見圖1，圖中l1和l2是機械臂連桿的長度，m1和m2是連桿的質量，q1和q2代表機械臂關節的轉動角度。根據圖1，使用Lagrange方程求解出雙關節水下機械臂的傳統動力學方程如式(1)所示[13]。

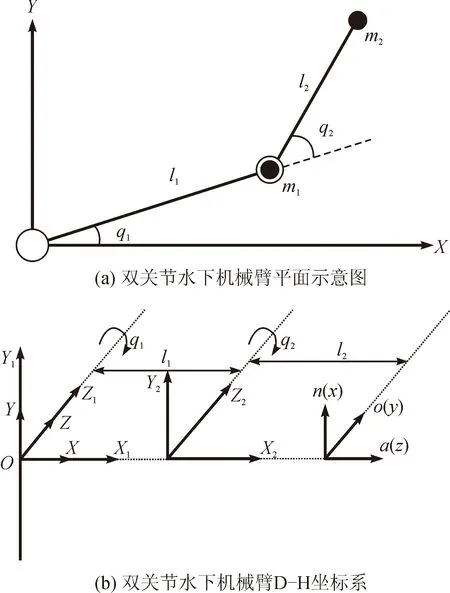
圖1 雙關節水下機械臂結構簡化示意圖Fig.1 Simplified schematic diagram for double-joint manipulator

(1)

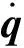
1.2 水下機械臂動力學建模

水下機械臂在水中受到的力分別為水流對靜止機械臂的沖擊力和機械臂在靜水中運動時所受的作用力。根據流體力學，物體單位長度在靜水中運動時的受到的作用力可以描述為：

(2)

式中：fd、fm、ff和fl分別為水阻力、附加質量力、浮力和升力。

本文研究的雙關節水下機械臂模型的連桿均為圓柱體，因此在進行受力分析時不用考慮升力帶來的影響。

Morison方程給出了水阻力和附加質量力的微分計算公式：

(3)

式中：ρ是水密度；D是連桿直徑；A是連桿垂直于水流速度方向上的投影面積；v是與速度相關的函數；Cd和Cm是水阻力系數與附加質量力系數，難以直接獲取精確值，一般選用經驗值[14]。

根據圖1中雙關節水下機械臂的D-H坐標系，繪制其運動模型示意圖，見圖2。

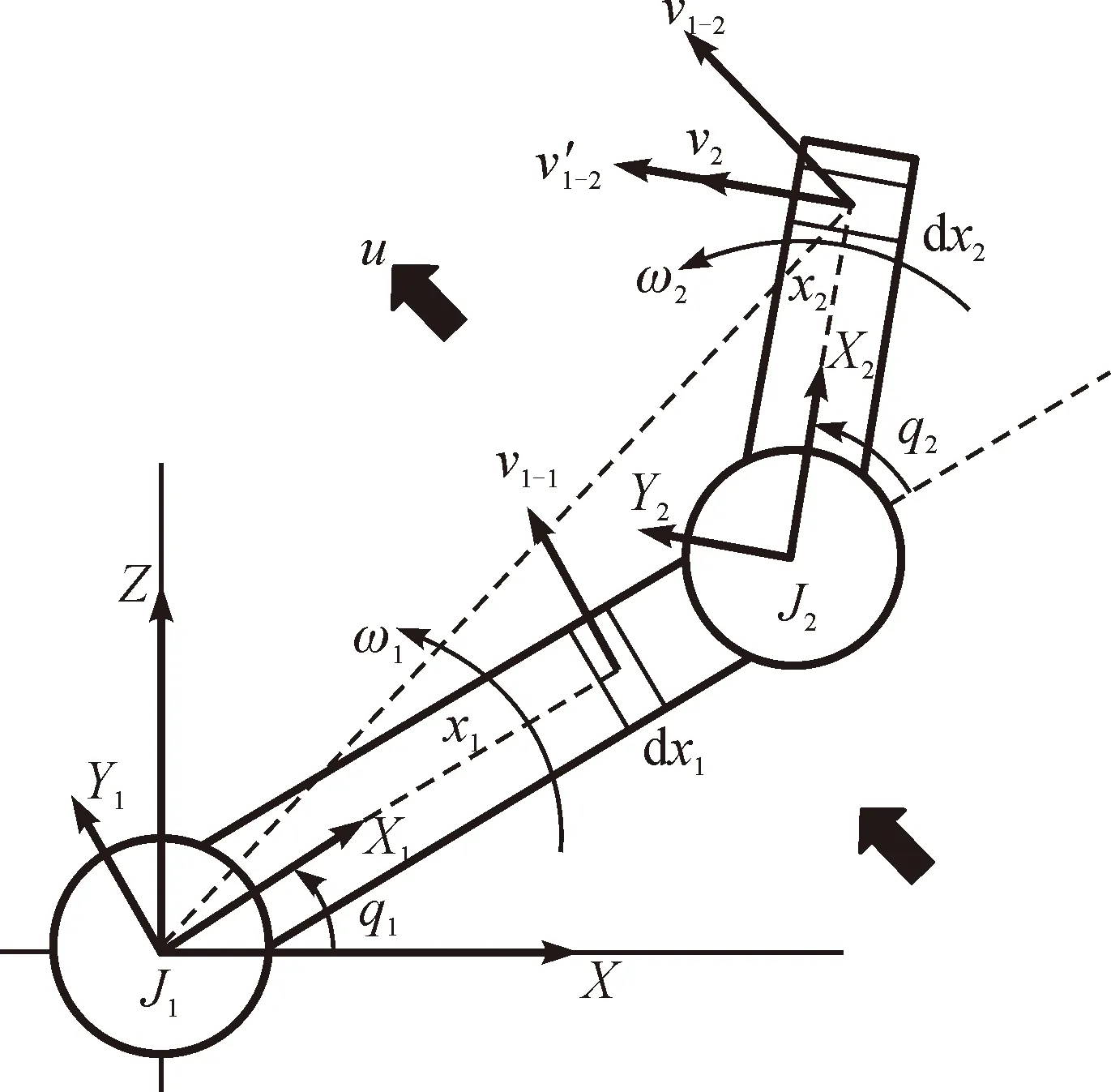
圖2 雙關節水下機械臂運動模型示意圖Fig.2 Schematic diagram for motion model of double-joint underwater manipulator

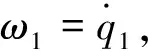
(4)

式中：c1=cosq1，c2=cosq2。

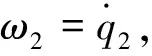
(5)

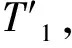
(6)

(7)

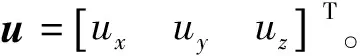
(8)

根據式(9)和式(10)求得機械臂關節J1與關節J2受到水流沖擊力矩T″1與T″2。

(9)

(10)

根據上述推導過程，可將雙關節水下機械臂關節在水中受到的水作用力矩歸納為TW：

(11)

假設雙關節水下機械臂各關節連桿的重心與浮心的位置重合，且重力與浮力的作用力方向相反，可根據下式求得機械臂各連桿的等效重力：

(12)

式中：mi為連桿i的質量；g為重力加速度；Vi為連桿i的體積；ρ為水密度；ρm為機械臂的等效密度。

根據式(12)與重力矩陣g求得雙關節水下機械臂的等效重力矩陣g′：

g′=

(13)

式中：c12=cos(q1+q2)。

將由式(11)求得的水作用力矩陣TW與式(13)求得的等效重力矩陣g′結合式(1)可以求得水下機械臂在水環境中的動力學模型：

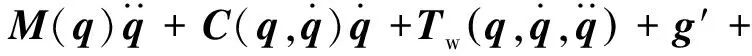
(14)

2 水下機械臂控制器設計

2.1 傳統滑模控制

定義滑模函數為：

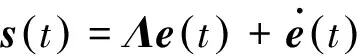
(15)

e(t)=qd-q

(16)

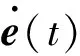
對式(15)進行求導可得：

(17)

(18)

f+εsgns+ks

(19)

式中：M′=M+Mw，C′=C+Cw。

2.2 分塊逼近RBF滑模控制

將式(19)中的不確定項整理得到：

(20)

由于式(20)中包含了多個不確定參數項，使用常規RBF神經網絡控制器對其進行整體逼近會產生逼近時間過長與逼近精度不足的問題。

為解決上述問題，本文使用由四個RBF神經網絡組成RBF神經網絡控制器對式(20)中的系數矩陣進行分塊逼近，再結合滑模控制算法設計水下機械臂控制器，控制器的原理框圖見圖3。

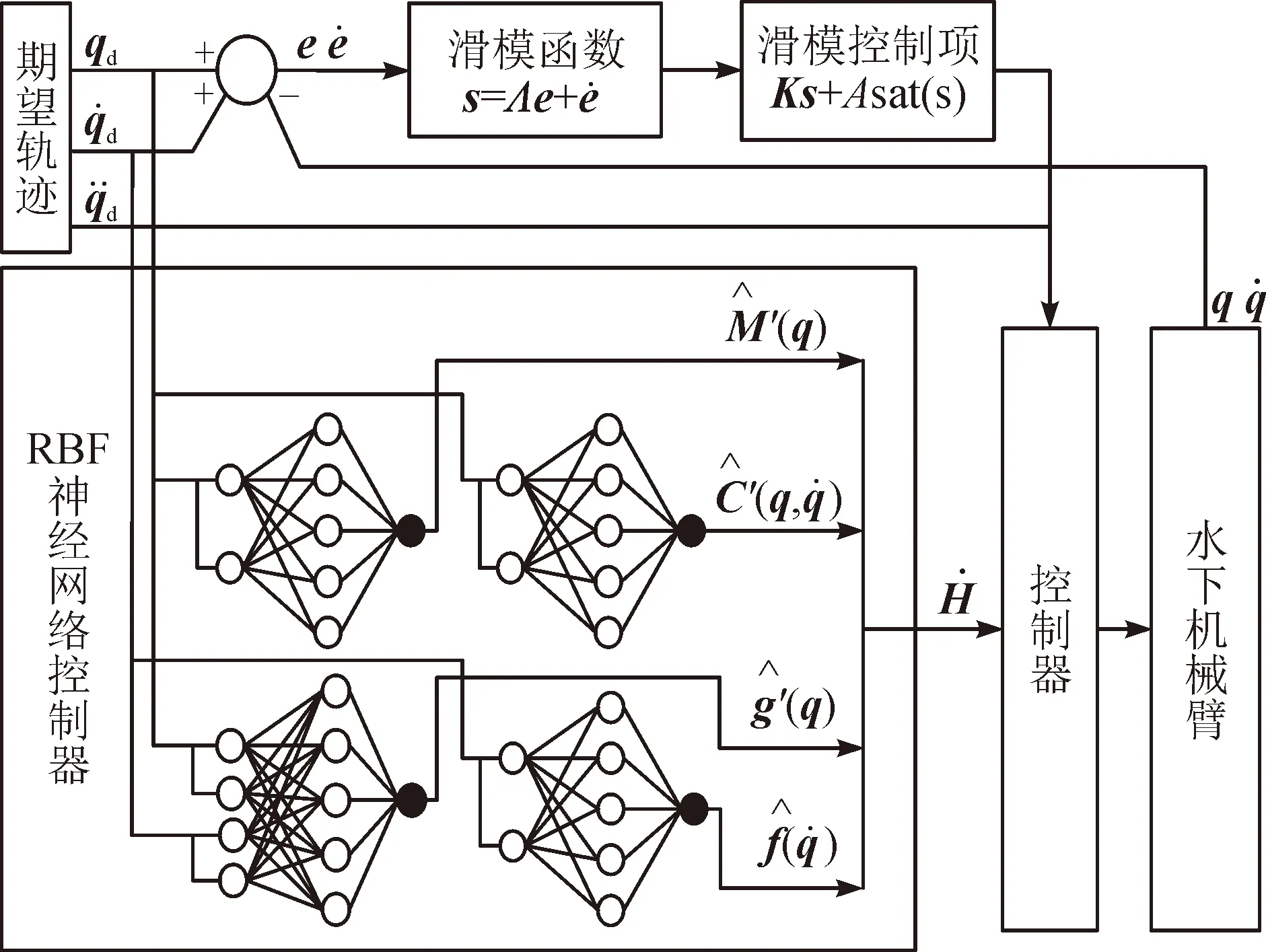
圖3 水下機械臂控制器設計原理框圖Fig.3 Underwater manipulator controller design principle block diagram

根據上圖中RBF神經網絡控制器的結構可知各RBF神經網絡的輸入分別為：

(21)

(22)

(23)

(24)

RBF神經網絡控制器的各網絡隱含層均包含五個神經元，神經元內部算子均為Gauss核函數：

(25)

式中：ci為第i個神經元的中心矢量，bi為神經元的基寬度。

各RBF神經網絡的自適應律分別為：

(26)

(27)

(28)

(29)

式中：FM′、FC′、Fg′與Ff均為正定矩陣。

(30)

式中：

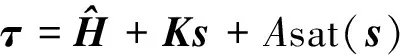
(31)

式中：K為控制系數矩陣，A為大于0的常數。Ks+Asat(s)用于消除外部干擾τd與神經網絡控制器的輸出誤差δ。

2.3 穩定性分析

定義正定的Lyapunov函數L：

(32)

對Lyapunov函數L進行求導可得：

(33)

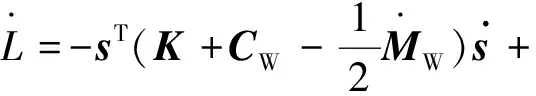
(34)

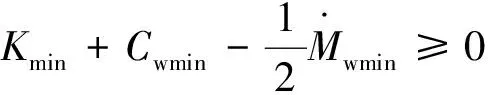
(35)

當A≥(‖δ‖+‖τd‖)時，有：

sT(τd-Asat(s)+δ)≤0

(36)

3 仿真分析

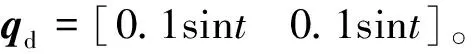
圖4中展示的是在雙關節水下機械臂仿真控制實驗中整體逼近型RBF神經網絡控制器與分塊逼近型RBF神經網絡控制器的輸出對比。

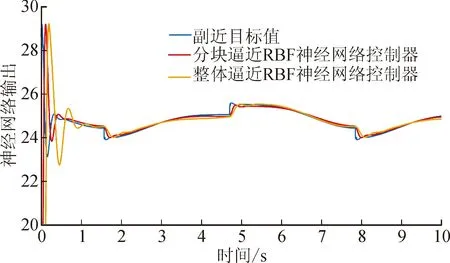
圖4 RBF神經網絡控制器輸出對比圖Fig.4 RBF neural network output comparison diagram

從上圖可以看出分塊逼近RBF神經網絡控制器在0.8 s附近實現了對目標值的逼近，整體逼近型RBF神經網絡控制器在1.2 s附近實現對目標值的逼近。結果表明使用多個RBF神經網絡對雙關節水下機械臂動力學模型中的不確定參數進行分塊逼近可以提高對實際模型的逼近速度，分塊逼近RBF神經網絡控制器相比于整體逼近RBF神經網絡控制器具有更好逼近效果。

不同控制算法下雙關節水下機械臂各關節的角度跟蹤曲線見圖5，角度的跟蹤誤差曲線見圖6，仿真實驗數據見表1。

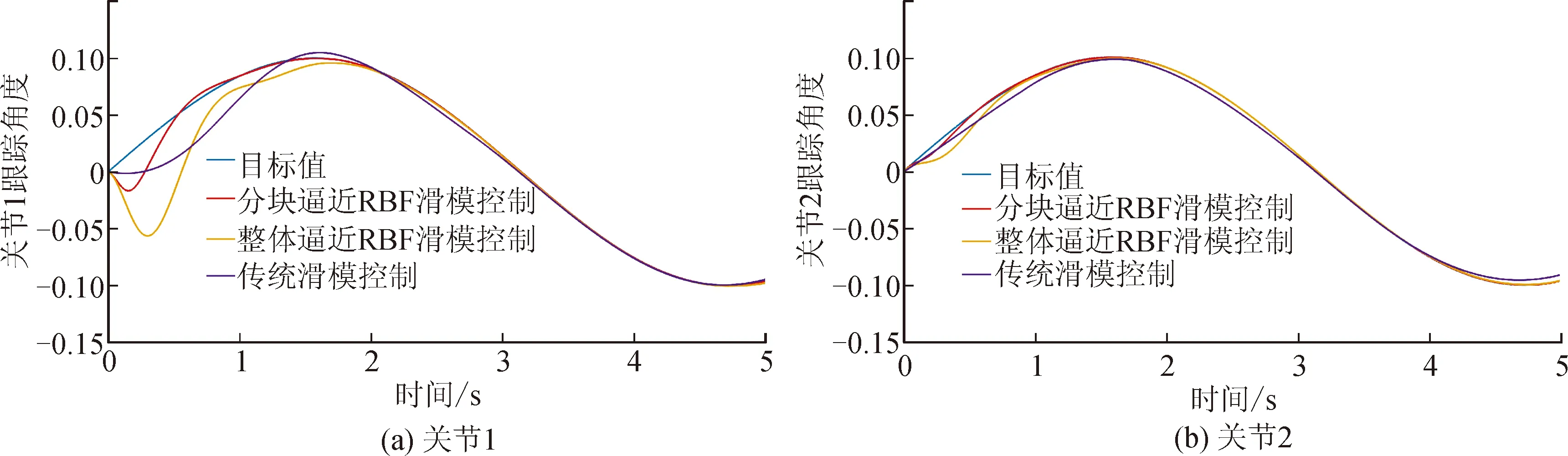
圖5 雙關節水下機械臂各關節角度跟蹤曲線Fig.5 Angel tracking curve of each joint of double-joint underwater manipulator

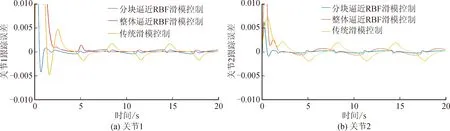
圖6 雙關節水下機械臂各關節角度跟蹤誤差曲線Fig.6 Angle tracking error curve of each joint of double-joint underwater manipulator

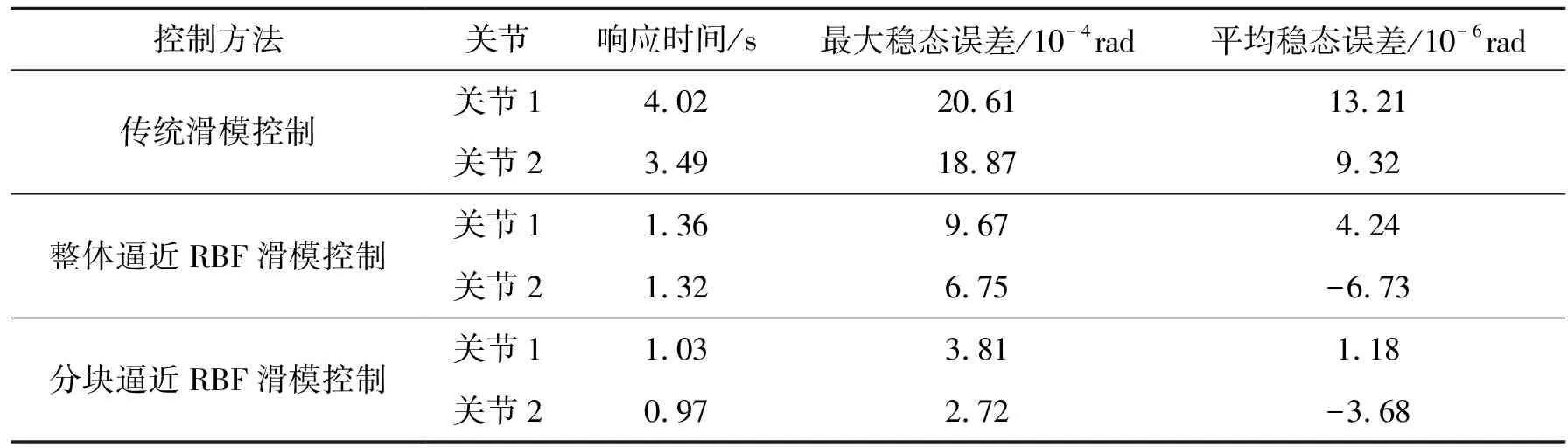
表1 仿真實驗數據分析表

通過表1中的數據對比可知，使用RBF神經網絡優化滑模控制算法可以明顯提升傳統滑模控制算法的性能。使用分塊逼近RBF滑模控制算法時，關節1和關節2的響應時間分別為1.03 s與0.97 s，最大穩態誤差分別為3.81×10-4rad與2.72×10-4rad，平均穩態誤差分別為1.18×10-6rad與-3.68×10-6rad。使用整體逼近RBF滑模控制算法時，關節1和關節2的響應時間分別為1.36 s與1.32 s，最大穩態誤差分別為9.67×10-4rad與6.75×10-4rad，平均穩態誤差分別為4.24×10-6rad與-6.73×10-6rad。

經對比，分塊逼近RBF滑模控制算法將水下機械臂的關節響應時間縮短了24%和27%，最大穩態誤差減少了60%和59%，平均穩態誤差減少了72%和45%。

從圖7所示的關節2控制輸入曲線圖可以看出，當控制律中使用開關函數時，關節2的控制輸入存在劇烈抖振，振動幅度為0.6 N·m。當控制律中使用飽和函數sat(s)時，關節2的控制輸入的抖振現象明顯減小，振動幅度為0.01 N·m。

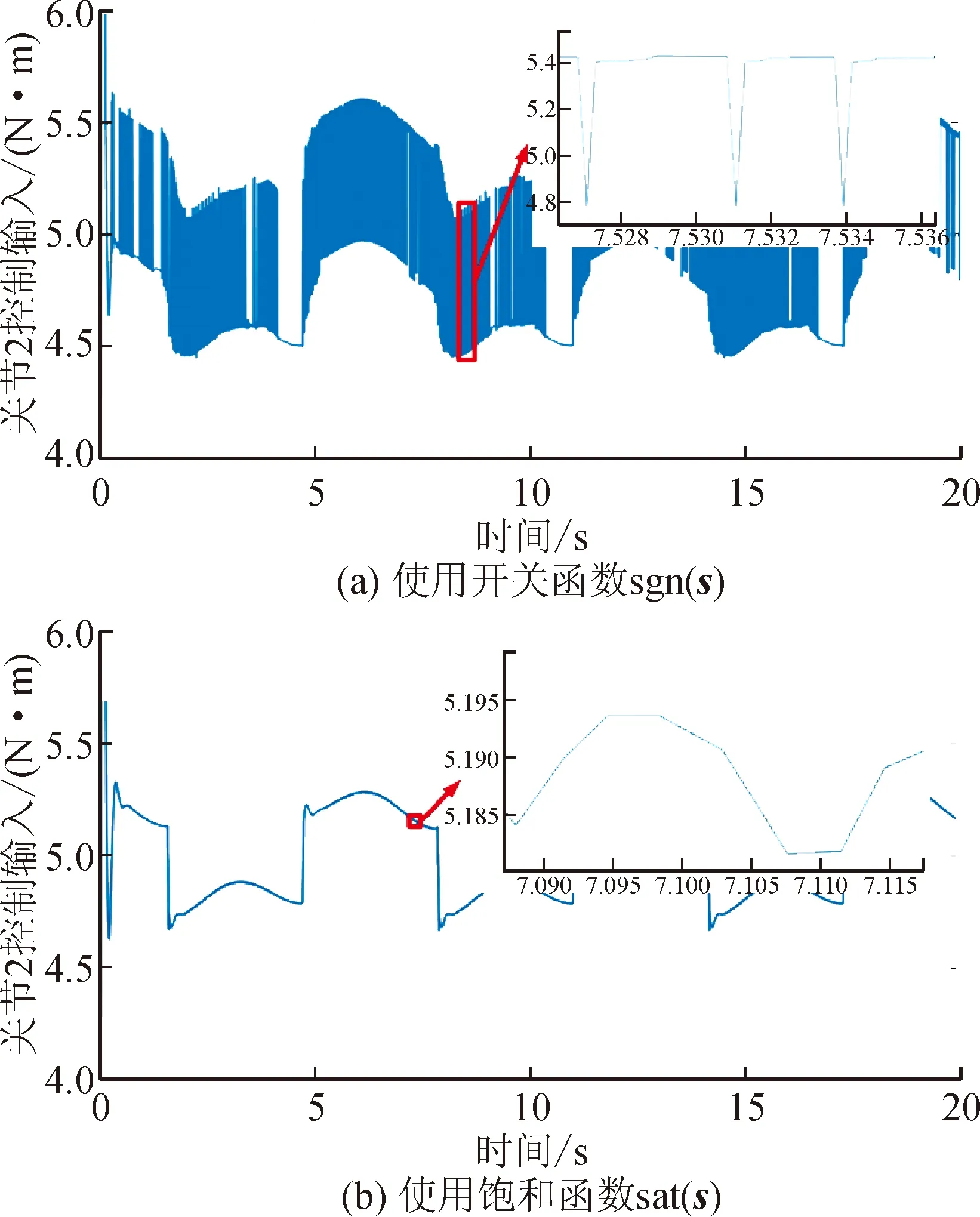
圖7 關節2控制輸入曲線Fig.7 Control input curve for joint 2

仿真實驗結果表明，本文提出的基于動力學模型分塊逼近的水下機械臂RBF滑模控制算法相比于傳統滑模控制和整體逼近RBF滑模控制可以大幅縮短水下機械臂控制系統的響應時間，降低控制系統的最大穩態誤差與平均穩態誤差，并能夠抑制控制系統的抖振效應，實現良好的控制效果。

4 結 論

1) 通過計算雙關節水下機械臂在水中運動時受到的水作用力矩，建立了雙關節水下機械臂在水環境中的動力學模型。

2) 結合水下機械臂的動力學模型，提出了一種分塊逼近RBF滑模控制算法，該算法縮短了對水下機械臂實際動力學模型的逼近時間，提升了逼近精度，從而縮短了控制系統的響應時間，提高了控制系統的控制精度；通過飽和函數改進了控制律，有效削弱了控制系統的抖振效應。仿真試驗結果表明該算法將水下機械臂的關節響應時間縮短至1 s，穩態精度提升至3×10-6rad，滿足水下機械臂的控制要求。