燒蝕磨損對某大口徑自行加榴炮動態響應的影響

郭俊行,樵軍謀,李宗虎,丁紅民

(西北機電工程研究所,陜西 咸陽,712009)

某大口徑自行加榴炮初速高、膛壓高,因此,身管壽命和射擊精度是該型火炮總體關鍵技術指標,膛線形式成為影響身管壽命和射擊精度的關鍵因素之一。膛線形式的選擇,有等齊膛線、漸速膛線、漸速-等齊混合膛線等技術途徑。一般認為,采用漸速膛線能夠減緩膛線導轉側磨損,改善膛線起始部的受力,而減小這個部位的磨損,有利于提高身管壽命[1-2]。相關研究認為炮口振動是影響射擊精度的重要因素之一,反后坐裝置布置對動力學響應有一定影響。文獻[3]通過對搖架變形及其與反后坐裝置相互作用的分析,研究了反后坐裝置在搖架上不同安裝方式對重復工作一致性的影響,但是僅為定性分析、沒有定量計算。文獻[4]應用非線性有限元理論,建立了某大口徑火炮的發射動力學模型,考慮了機構之間的接觸碰撞關系,采用數值計算研究了復進機和駐退機的不同固定方式和不同布置位置對載荷傳遞規律和炮口振動的影響。文獻[5]建立了全炮剛柔耦合發射動力學模型,研究了反后坐裝置布局對炮口振動的影響。但是,以上研究并沒有考慮彈丸運動。以上研究及相關工程實踐均表明,反后坐裝置布置對動力學響應有一定影響,采用反后坐裝置對射擊平面對稱布置的方案能夠減小對發射系統的影響從而改善射擊精度。文獻[6]基于SPH-FEM方法建立了全炮發射動力學模型,通過對比仿真結果和試驗數據驗證了該模型的有效性,研究了彈丸不平衡因素及裝填姿態等炮口振動的影響。文獻[7-8]建立了燒蝕后身管的動力學模型,研究了燒蝕磨損對擠進的影響。以上研究沒有考慮燒蝕等因素對火炮系統振動的影響,該研究仍然有待深入。

本文以采用反后坐裝置全對稱布置、混合膛線的某大口徑自行加榴炮為例,研究燒蝕磨損對其動力學響應的影響;采用有限元理論建立發射動力學模型,研究了內膛不同磨損程度對火炮動態響應的影響,為未來發展高精度、長壽命大口徑火炮提供理論參考。

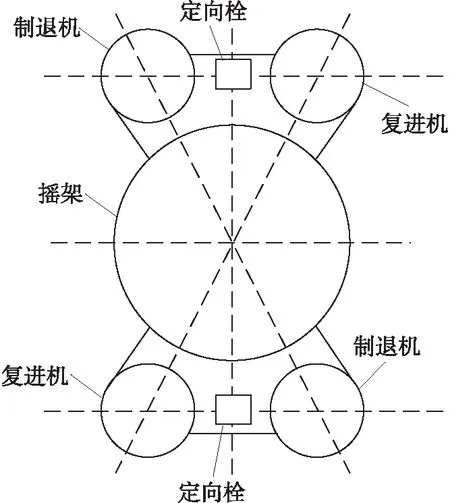
圖1 反后坐裝置及定向栓布置方案

1 火炮結構及有限元模型

1.1 火炮起落部分結構

該自行火炮反后坐裝置及定向栓布置方案見圖1。如圖1所示,復進機、制退機、定向栓關于火炮軸線對角對稱布置。起落部分采用實體單元和殼體單元為主的網格劃分方法[9],建立有限元網格,如圖2所示。

圖2 自行火炮起落部分有限元模型

1.2 燒蝕身管有限元模型

經過一定射擊次數后,身管燒蝕明顯。圖3是某大口徑火炮身管實測的陰線、陽線的擴大系數隨位置變化圖,圖中,陽線、陰線擴大系數分別定義為

(1)

(2)

式中:dl為陽線原始直徑,d′l為燒蝕后陽線直徑;dg為陰線原始直徑,d′g為燒蝕后陰線直徑;z為測量位置距膛線起始點的距離。由圖可見,經過一定射擊次數的身管,陰線、陽線的擴大倍數在沿身管長度方向是不同的,在膛線起始段燒蝕明顯,而炮口附近燒蝕較小。圖3是某火炮實際測徑數據,由圖可見,膛線起始部向前25.4 mm處陽線直徑擴大量為2.1 mm。

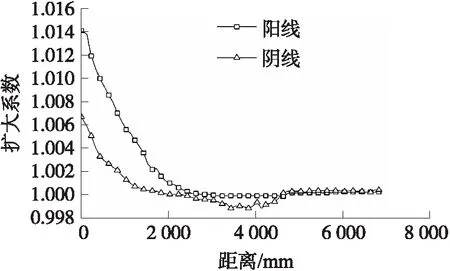
圖3 某大口徑火炮身管內膛直徑燒蝕情況

本文提出了一種燒蝕身管有限元模型建模方法。首先,使用UG軟件建立幾何母模型,如圖4(a)所示,準確建立其坡膛的幾何尺寸,簡化了膛線橫截面上的圓角,膛線部分為拉伸特征。其次,使用HyperMesh等軟件對其進行網格劃分,得到圖4(b)所示有限元母模型。再編程實現坐標徑向放大、旋轉變換,得到混合膛線身管燒蝕后的有限元網格,見圖4(c)。對某樣炮進行310發和581發射擊,獲得實際測徑數據,其膛線起始部向前25.4 mm處直徑分別擴大了2.1 mm和4.6 mm,經過統計射擊數據,分別對應射彈當量數(EFC)240和540。依據膛線部分實測尺寸建立了2個燒蝕身管有限元模型,其膛線部分尺寸均有不同程度的磨損,以下簡稱“直徑擴大2.1 mm”和“直徑擴大4.6 mm”。

圖4 燒蝕身管建模方法

彈丸網格模型見圖5,彈帶部分采用光滑粒子單元加實體單元建模[10-13],該方法能夠應用于大口徑火炮彈丸運動及炮口振動分析[6]。

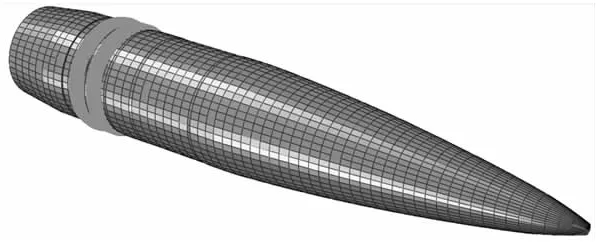
圖5 彈丸網格模型

1.3 坐標系

取炮口方向為z軸正向,從炮尾看過去向左為x軸正向,向上為y軸正向。炮口用炮口制退器前端面中心來代替,射擊過程中該中心點偏離原始位置,即炮口響應。由于該端面本身基本不變形,它的運動僅僅為平移和端面外法線的轉動,即由平動位移和旋轉角位移構成。約定炮口在x向和y向的位移為s1和s2,s1向左為正,s2向上為正;繞x軸和y軸轉動的角度為α1和α2,即高低和方向角位移,α1向下為正,α2向左為正;具體見圖6。

圖6 炮口振動位移和角位移方向示意圖

1.4 彈炮耦合動力學模型

根據火炮結構的特點,搖架與后坐部分之間通過襯套支撐,同時有定向栓限制后坐部分的旋轉,故定義搖架前后銅襯套內表面與身管圓柱部外表面、定向栓室表面和定向栓之間的接觸關系。火炮在靜止狀態下受重力作用產生自重變形,是發射時的初始幾何構型。首先,建立靜態分析步求解其變形和應力,再導入靜態分析結果進行下一步分析。圖7是起落部分在0°射角時的靜力變形求解結果,從云圖可以看出,最大位移為11.48 mm,位于炮口制退器。

圖7 起落部分在0°射角時的自重變形

為對比燒蝕對動態響應的影響,分別建立有限元模型。計算條件選為常溫全裝藥,內彈道計算出的壓力曲線見圖8。彈丸定心部直徑取為下偏差,彈丸無質量偏心,高低射角和方向射角取0°。

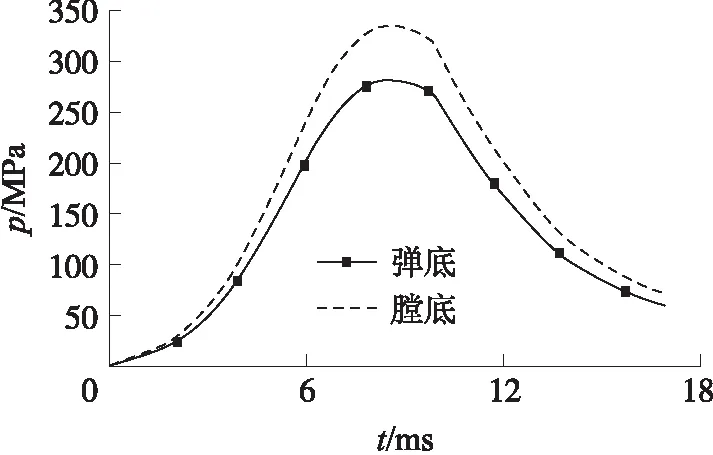
圖8 某裝藥條件壓力曲線

在有限元模型中,在炮尾和搖架之間建立非線性彈簧和非線性阻尼單元,分別用來模擬復進機和制退機。經典內彈道理論認為,隨著彈丸行程的增大,彈后空間分布的燃氣壓力隨時間和空間變化,動態地作用在部分身管內膛表面上。根據經典內彈道理論,假設彈后空間的壓力分布是一個二次曲線,可以通過膛底壓力、彈底壓力、彈丸位置,依據公式計算得到。由于在前處理中很難將彈后空間的燃氣壓力動態地加載到內膛表面,為此本研究對Abaqus/Explicit提供的VDLOAD子程序進行二次開發,以實現壓力動態加載,程序流程如圖9所示。首先,依據分析步時間,由彈丸行程、后坐行程曲線查表得出彈丸、膛底所處的位置,即可判斷內膛表面上某點處于彈前空間還是彈后空間;如果該點處于彈前空間,壓力載荷為0;如果是彈后空間,從內彈道曲線上插值得出膛底壓力、彈底壓力,再依據壓力分布插值得到壓力載荷。

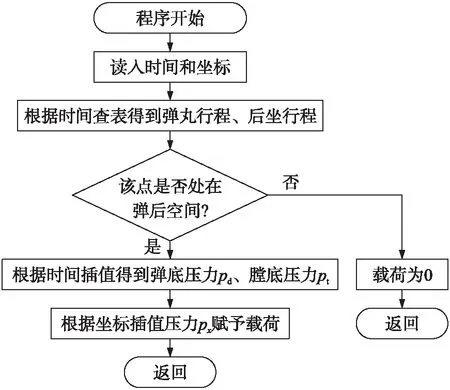
圖9 使用VDLOAD子程序實現布爾頓力加載的程序流程圖

彈丸在膛內運動時彈帶和內膛表面接觸,定心部也可能與內膛表面接觸,定義定心部表面、彈帶和內膛的接觸關系;后坐部分支撐在搖架的襯套上,身管外表面和襯套接觸,定義身管外表面和襯套的接觸關系。

2 計算結果及討論

2.1 內彈道符合計算

圖10是有限元模型計算得到的彈丸加速度a曲線。從圖中可以看出,所建立的動力學有限元模型計算出的彈丸加速度與內彈道計算結果符合良好。

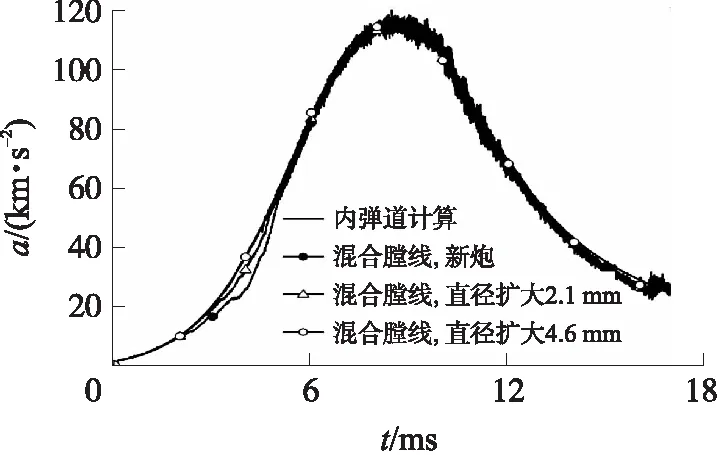
圖10 模型計算得到的彈丸加速度曲線

下文圖中均采用混合膛線條件。

圖11是有限元模型計算得到的彈丸導轉力矩M隨時間t和彈丸行程l變化曲線。從圖中可以看出,所建立的動力學有限元模型計算出的彈丸導轉力矩與內彈道計算結果[1]符合良好。

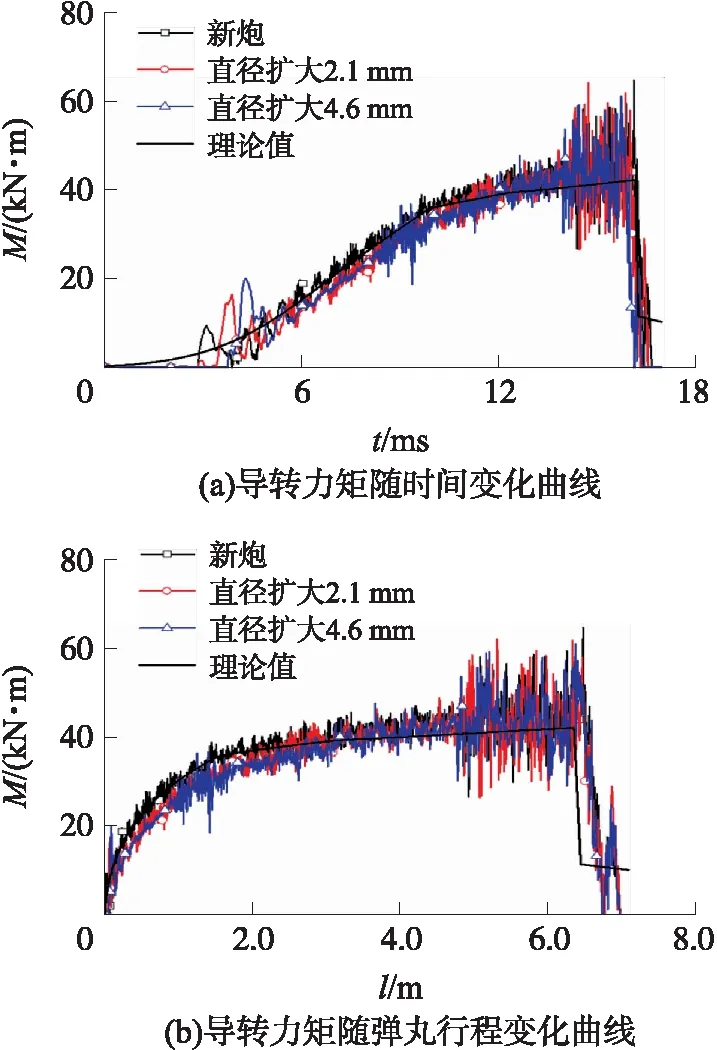
圖11 有限元計算得到的導轉力矩隨時間和彈丸行程變化曲線

2.2 彈丸前定心部力

圖12是有限元模型計算得到的彈丸前定心部受x方向接觸力Fx、y方向接觸力Fy變化曲線。

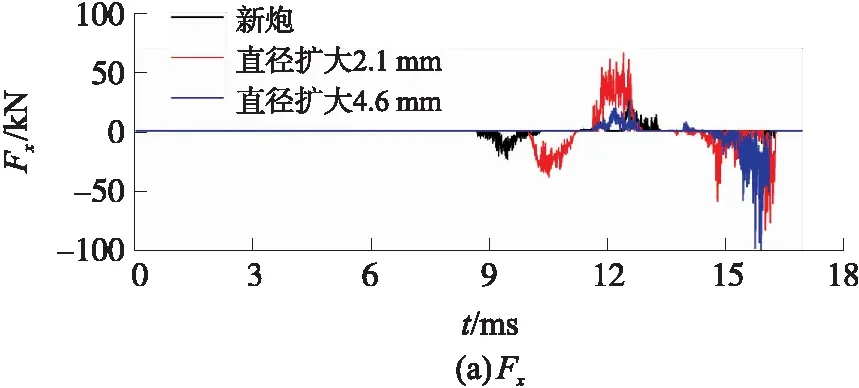
圖12 有限元計算得到的彈丸前定心部力變化曲線

從圖12中可以看出,在新炮時定心部力持續的時間很短,彈丸在運動時與內膛碰撞然后彈回。在燒蝕磨損后,定心部力持續的時間逐漸增長,定心部力逐漸增大。

2.3 炮口振動響應

圖13、圖14是有限元模型計算得到的炮口振動響應曲線,圖中,s1為左右位移,s2為高低位移,α1為左右角位移,α2為高低角位移,v1為左右速度,v2為高低速度,ω1為左右角速度,ω2為高低角速度。

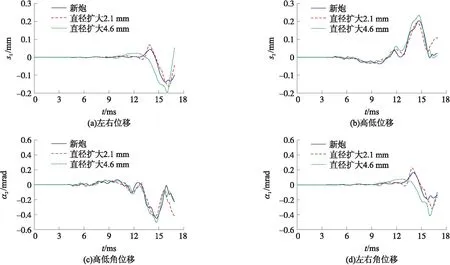
圖13 仿真得到的炮口振動位移及角位移曲線

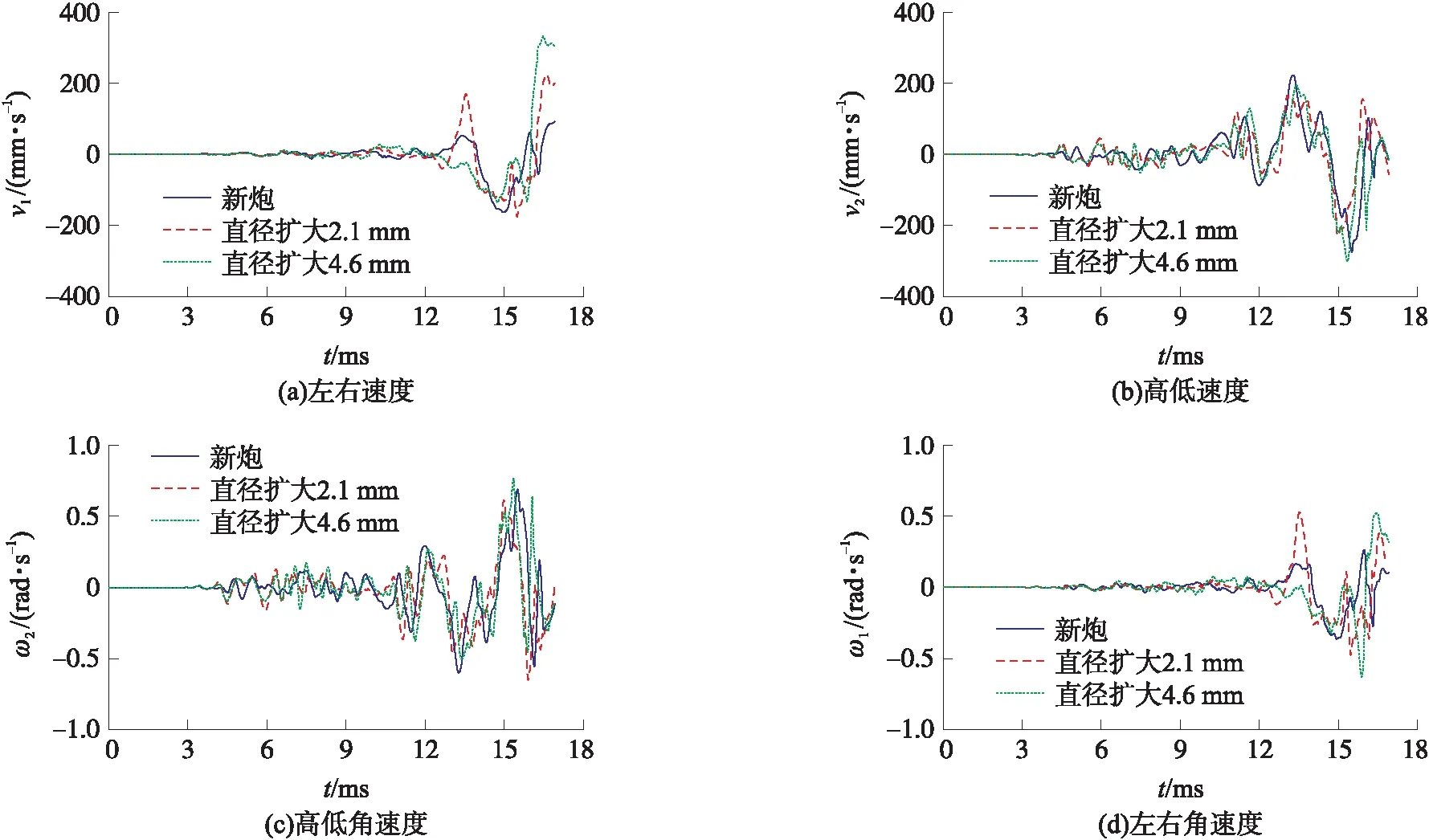
圖14 仿真得到的炮口振動速度及角速度曲線

從圖13、圖14中可以看出,隨著燒蝕磨損量增加,炮口振動位移增加不明顯,炮口振動速度有所增大。炮口點左右線速度和角速度有增大趨勢,而高低線速度和角速度增加不明顯,這與火炮炮口振動產生的機理有關。以后坐部分為研究對象,發射過程中主要外力有反后坐裝置力、慣性力、布爾頓力、彈丸作用力等[6]。由于采用了反后坐裝置沿火炮軸線對稱布置方案,反后坐裝置力對炮膛軸線力矩有互相抵消的趨勢。慣性力和布爾頓力總是引起火炮在高低方向的振動,其影響反映在高低位移曲線上。身管受彈丸作用力與很多因素有關,前定心部力會受到彈炮間隙影響,有一定的隨機性,引起炮口振動的隨機性。文獻[6]研究結果表明,炮口振動受彈丸與內膛作用影響明顯。從圖12中可以看出,在采用混合膛線時彈丸轉速逐漸增加,彈丸接觸力隨彈丸行程增加;由圖14可以看到,隨著內膛磨損量增加,炮口振動速度逐漸增大。

3 結論

本文研究了內膛燒蝕磨損對某大口徑自行加榴炮動態響應的影響。采用有限元方法建立了起落部分的有限元模型;依據內膛直徑實測數據,建立了2種燒蝕磨損程度的身管模型;仿真了膛內時期起落部分的動態響應,得到了彈丸運動加速度、導轉力矩、前定心部力和炮口點振動。經過仿真分析可知,該大口徑自行加榴炮采用混合膛線時隨著燒蝕磨損增大,彈丸的定心部力逐漸增大,炮口振動位移增加不明顯,炮口振動速度有所增大。