設(shè)置支撐的廣義Maxwell阻尼耗能系統(tǒng)非均勻非平穩(wěn)地震響應(yīng)分析

李創(chuàng)第 王博文 昌明靜

（廣西科技大學(xué)土木建筑工程學(xué)院，柳州545006）

0 引 言

地震整個(gè)過程，一般都是非平穩(wěn)隨機(jī)過程［1］，具有頻率和強(qiáng)度的非平穩(wěn)隨機(jī)特性［1］，目前地震的非平穩(wěn)隨機(jī)響應(yīng)分析大多受限于均勻調(diào)制隨機(jī)激勵(lì)情形，非均勻非平穩(wěn)激勵(lì)的研究正日益受到國(guó)際學(xué)術(shù)界與工程界的高度重視［2-4］。因此，研究非均勻非平穩(wěn)隨機(jī)地震響應(yīng)分析具有十分重要的實(shí)際意義。平穩(wěn)激勵(lì)是研究非均勻非平穩(wěn)隨機(jī)地震的基礎(chǔ)，其激勵(lì)模型主要有白噪聲激勵(lì)模型［5］、Kanai-Tajimi 模型［6］、Clough-Penzien 模型［7］、胡聿賢模型［8］等，其中Kanai-Tajimi 地震激勵(lì)模型具有符合地震動(dòng)特點(diǎn)和表達(dá)式相對(duì)簡(jiǎn)單的特點(diǎn)而受到廣大科研人員的研究［9］。

減震工程中，為減小結(jié)構(gòu)體系的地震動(dòng)響應(yīng)，通常采用增加結(jié)構(gòu)阻尼的方法，其中黏彈性阻尼裝置可以有效提供阻尼被廣泛采用［10］。描述黏彈性阻尼器的力學(xué)模型主要有Maxwell［11］、GHM［11］、分?jǐn)?shù)導(dǎo)數(shù)［11］、Kelvin［11］等，以Maxwell 模型基礎(chǔ)可擴(kuò)展為擬合精度較高的廣義Maxwell 阻尼器模型，對(duì)于工程上實(shí)際應(yīng)用的線性流體黏彈性阻尼器和線性固體黏彈性阻尼器，其本構(gòu)關(guān)系均可用參數(shù)足夠多的廣義Maxwell 模型精確表示，且廣義Maxwell 模型對(duì)流體和固體黏彈性阻尼器本構(gòu)關(guān)系的實(shí)驗(yàn)數(shù)據(jù)擬合精度均優(yōu)于分?jǐn)?shù)導(dǎo)數(shù)模型和Shen and Soong 模型。因此采用廣義Maxwell模型分析黏彈性耗能結(jié)構(gòu)的動(dòng)力性能具有較好的工程應(yīng)用價(jià)值。

在實(shí)際工程中，阻尼器需要與支撐串聯(lián)安裝［12］，我國(guó)《建筑抗震設(shè)計(jì)規(guī)范》［13］通過限制支撐的最小剛度，以確保支撐與阻尼器串聯(lián)系統(tǒng)發(fā)揮或接近純阻尼器的功效，故耗能系統(tǒng)響應(yīng)分析要考慮支撐的影響［14］。由于地震的非平穩(wěn)隨機(jī)特性，地震發(fā)生會(huì)首先引起支撐、阻尼器等結(jié)構(gòu)保護(hù)系統(tǒng)的破壞，進(jìn)而導(dǎo)致結(jié)構(gòu)體系的損傷甚至毀滅，目前相關(guān)規(guī)范明確要求耗能減震系統(tǒng)構(gòu)件在結(jié)構(gòu)設(shè)計(jì)基準(zhǔn)期內(nèi)應(yīng)具備足夠的變形、耗能能力和良好的抗震動(dòng)力可靠度［13-14］，故結(jié)構(gòu)及結(jié)構(gòu)保護(hù)系統(tǒng)響應(yīng)方法的建立，對(duì)于分析抗震動(dòng)力可靠度和抗震設(shè)計(jì)方法的建立具有重要價(jià)值。

針對(duì)結(jié)構(gòu)響應(yīng)的功率譜密度計(jì)算方法，林家浩提出了高效的虛擬激勵(lì)法，將非平穩(wěn)振動(dòng)分析轉(zhuǎn)化為簡(jiǎn)諧振動(dòng)分析和確定性時(shí)間歷程分析，在計(jì)算步驟簡(jiǎn)化的基礎(chǔ)上仍保持理論上的高度精確性［15］。該方法被廣泛應(yīng)用于結(jié)構(gòu)動(dòng)力響應(yīng)、風(fēng)工程、海洋工程、偏微分方程的求解等眾多領(lǐng)域［16］，但是目前關(guān)于設(shè)置支撐的黏彈性阻尼器耗能減震結(jié)構(gòu)基于虛擬激勵(lì)法的非平穩(wěn)響應(yīng)分析尚未建立。

鐘萬(wàn)勰提出的精細(xì)積分法，對(duì)于計(jì)算機(jī)求解指數(shù)矩陣的精度有顯著的提高，能有效降低因精細(xì)劃分所引起的誤差［17］；這種積分方法雖然不是提供解析解公式，但其數(shù)值計(jì)算結(jié)果卻是高度準(zhǔn)確的［18］。目前林家浩提出了簡(jiǎn)諧、多項(xiàng)式簡(jiǎn)諧、指數(shù)簡(jiǎn)諧型精細(xì)積分格式，已應(yīng)用于無阻尼器結(jié)構(gòu)的均勻非平穩(wěn)隨機(jī)響應(yīng)高效分析［19］，但僅對(duì)于特定形式的激勵(lì)效率較高，對(duì)于較一般的均勻與非均勻調(diào)制型非平穩(wěn)隨機(jī)地震激勵(lì)具有一定的局限性。

本文為建立黏彈性耗能結(jié)構(gòu)及其保護(hù)系統(tǒng)的抗震分析與設(shè)計(jì)方法，對(duì)設(shè)置支撐的廣義Maxwell阻尼耗能系統(tǒng)隨機(jī)地震響應(yīng)的數(shù)值分析方法進(jìn)行了系統(tǒng)研究。首先，采用設(shè)置支撐的廣義Maxwell阻尼耗能系統(tǒng)進(jìn)行建模；然后，基于高效的虛擬激勵(lì)法，獲得了非均勻的精細(xì)積分較一般精確格式，最后解出廣義Maxwell 阻尼耗能系統(tǒng)的均勻與非均勻非平穩(wěn)地震響應(yīng)方差，通過算例驗(yàn)證本文方法的正確性，為黏彈性阻尼耗能系統(tǒng)在非均勻非平穩(wěn)地震激勵(lì)下的響應(yīng)分析提供了方法。

1 結(jié)構(gòu)運(yùn)動(dòng)方程

1.1 廣義Maxwell阻尼器模型的本構(gòu)關(guān)系

設(shè)廣義Maxwell阻尼器受力為PQ(t)，如圖1所示，其中標(biāo)準(zhǔn)Maxwell 阻尼器單元的個(gè)數(shù)為n，阻尼器的平衡剛度為k0，阻尼器第i個(gè)阻尼單元的剛度和阻尼分別為ki和ci，阻尼器相對(duì)于地面位移為xQ。

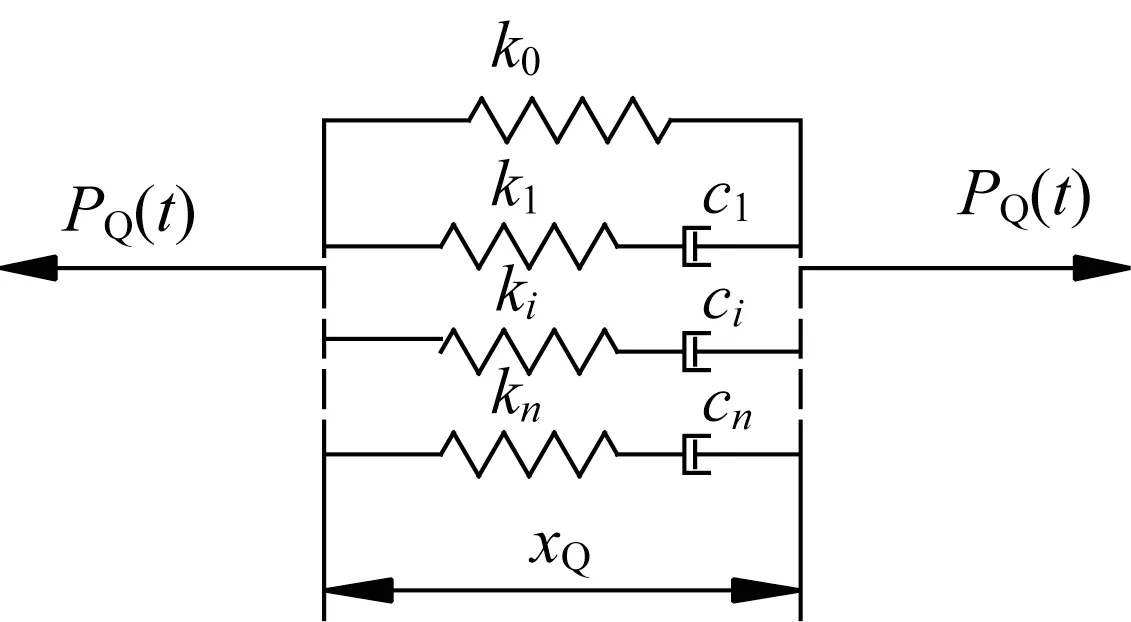
圖1 廣義Maxwell阻尼器模型Fig.1 General Maxwell damper model

那么阻尼器受力可表示為［10］：

式中：

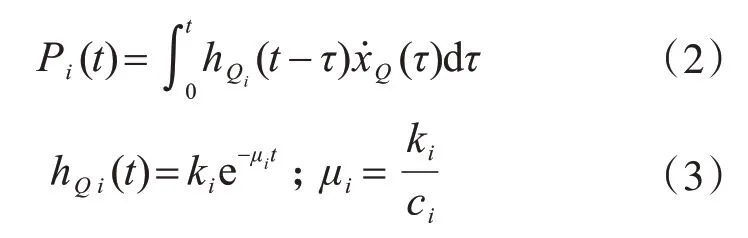
Pi(t)、hQi(t)、μi分別為阻尼器第i 個(gè)阻尼單元的阻尼力、松弛函數(shù)、松弛時(shí)間倒數(shù)。

由式（2）和式（3），可得：

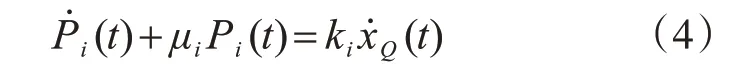
1.2 支撐與阻尼器的關(guān)系

工程實(shí)際中阻尼器一般與支撐串聯(lián)安裝，以產(chǎn)生更好的減震效果，如圖2 所示，支撐剛度為kb，支撐相對(duì)于地面位移為xb，結(jié)構(gòu)相對(duì)于地面位移為x。

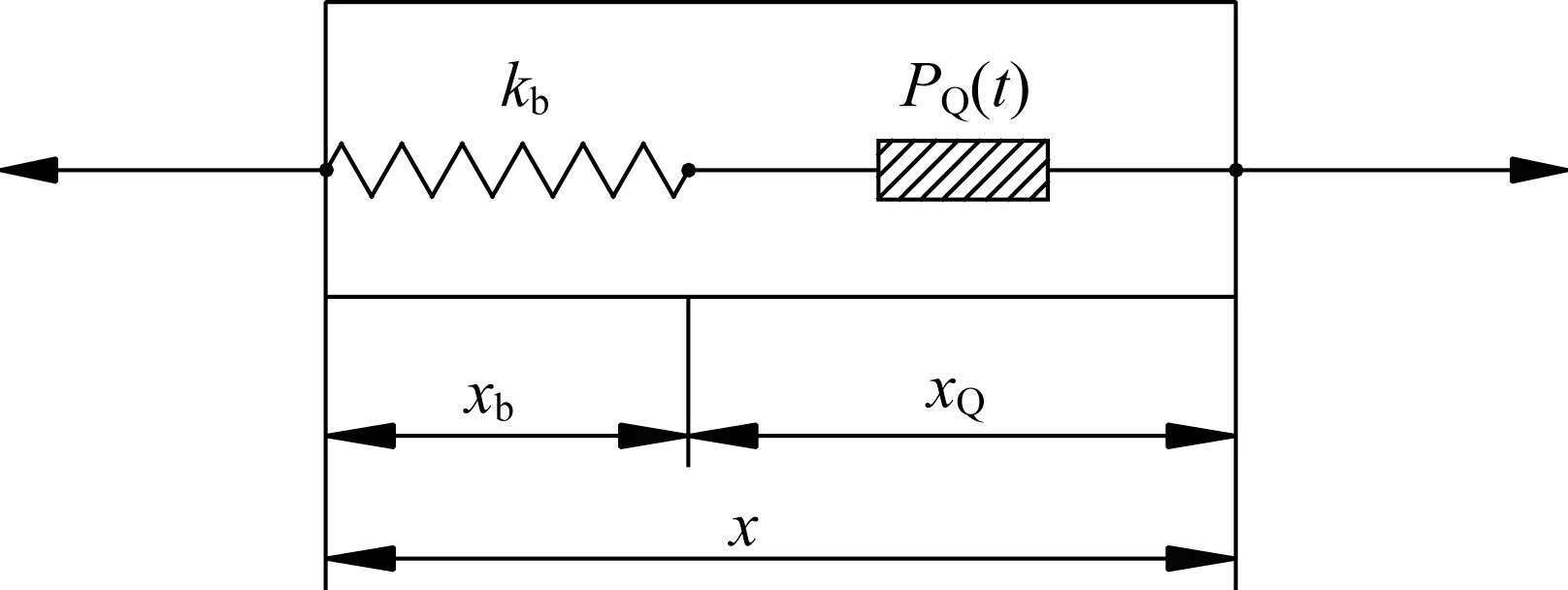
圖2 設(shè)置支撐的廣義Maxwell阻尼器模型Fig.2 General Maxwell damper model with support

那么支撐位移xb與結(jié)構(gòu)位移x、阻尼器位移xQ之間的關(guān)系為

設(shè)支撐的受力為Pb(t)，由于串聯(lián)安裝故支撐受力與阻尼器受力PQ(t)相同，即

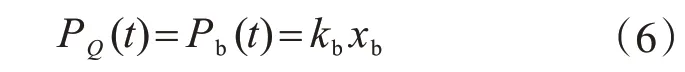
1.3 結(jié)構(gòu)運(yùn)動(dòng)方程的建立

如圖3 所示，設(shè)單自由度設(shè)置支撐的廣義Maxwell 阻尼減震系統(tǒng)質(zhì)量、剛度、阻尼分別為m、k、c，在地震動(dòng)激勵(lì)作用下，結(jié)構(gòu)運(yùn)動(dòng)方程可表示為

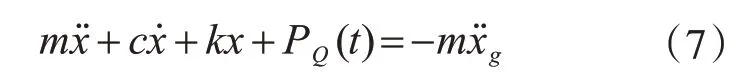
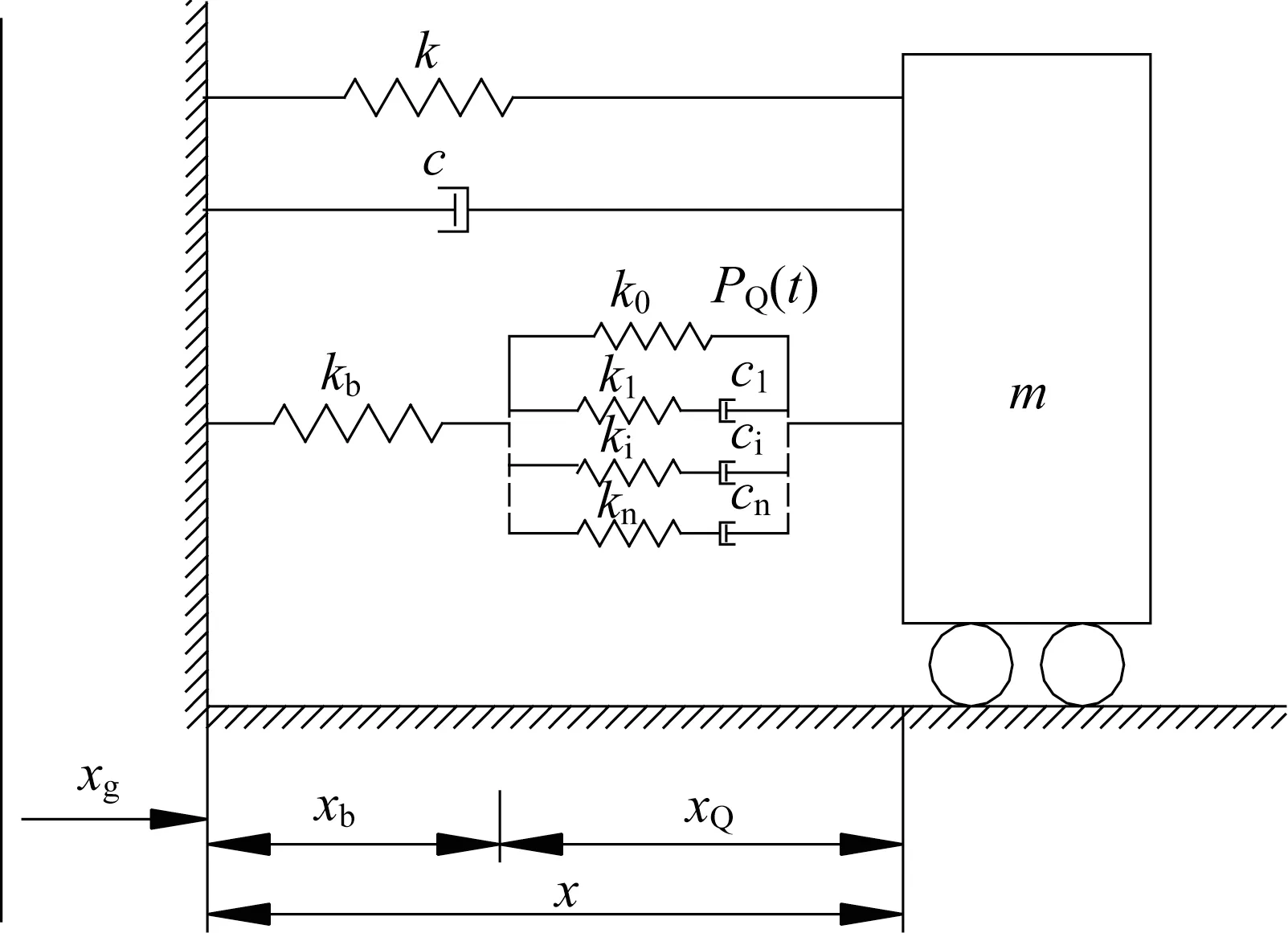
圖3 結(jié)構(gòu)模型Fig.3 Model of structure

將式（5）代入式（6），同時(shí)考慮式（1）、式（7）和式（6），可以寫為

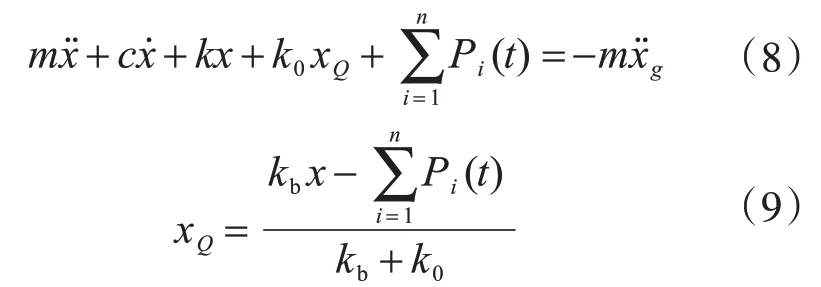
將式（9）分別代入式（8）和式（4），最終可得：

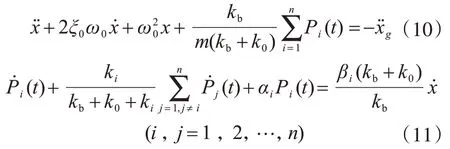
式中：

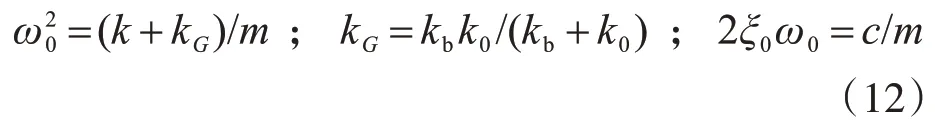
1.4 擴(kuò)階方程的建立

令

式（13）、式（10）和式（11）以擴(kuò)階的形式表示為

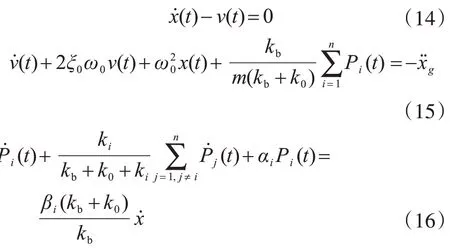
式中：

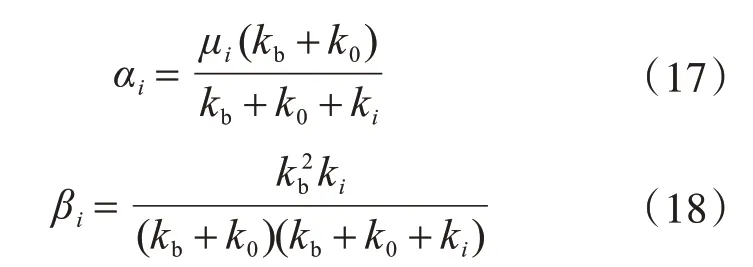
寫成矩陣形式為

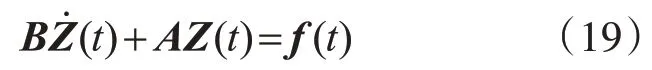
式中：

2 非平穩(wěn)隨機(jī)地震響應(yīng)分析的虛擬激勵(lì)法

2.1 非均勻非平穩(wěn)地震激勵(lì)模型

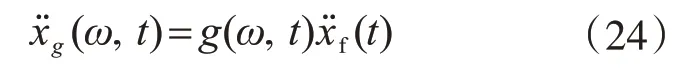
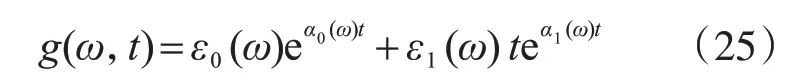
2.2 非均勻非平穩(wěn)地震響應(yīng)分析的虛擬激勵(lì)法

根據(jù)虛擬激勵(lì)法原理［15］將式（1）中替換為可得：

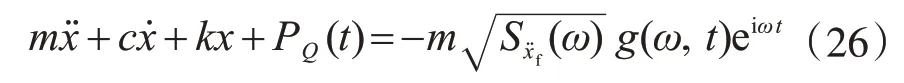
式（19）可改寫為

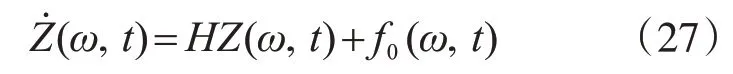
對(duì)于多自由度耗能結(jié)構(gòu)體系同樣也可化為上式，同樣可得多自由度耗能結(jié)構(gòu)體系響應(yīng)解析解。

式中：

式（27）的通解為齊次解與特解之和，即

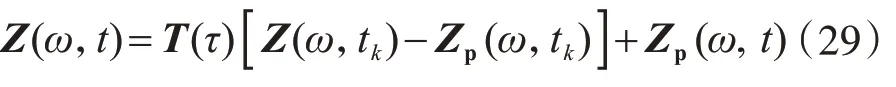
式中：積分步長(zhǎng)t ∈[tk，tk+1]，τ=t-tk；關(guān)于指數(shù)矩陣T(τ)的精細(xì)計(jì)算，詳見文獻(xiàn)［19］。

3 非均勻精細(xì)積分較一般精確格式

假定在積分步長(zhǎng)t ∈[tk，tk+1]內(nèi)荷載按較一般規(guī)律變化，則由式（25）和歐拉公式可得：

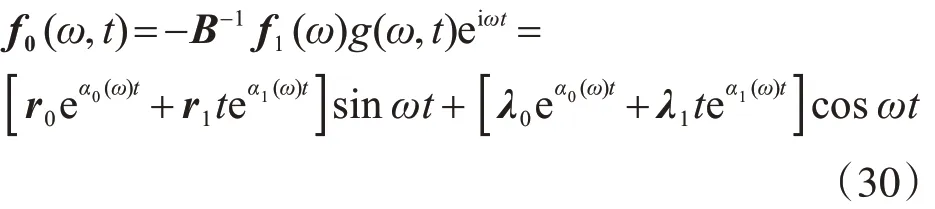
式中：

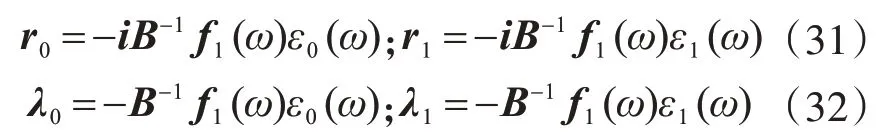
將式（30）代入方程式（27），可得方程的特解Zp(ω，t)為

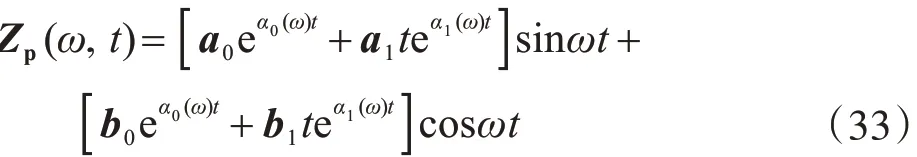
式中：

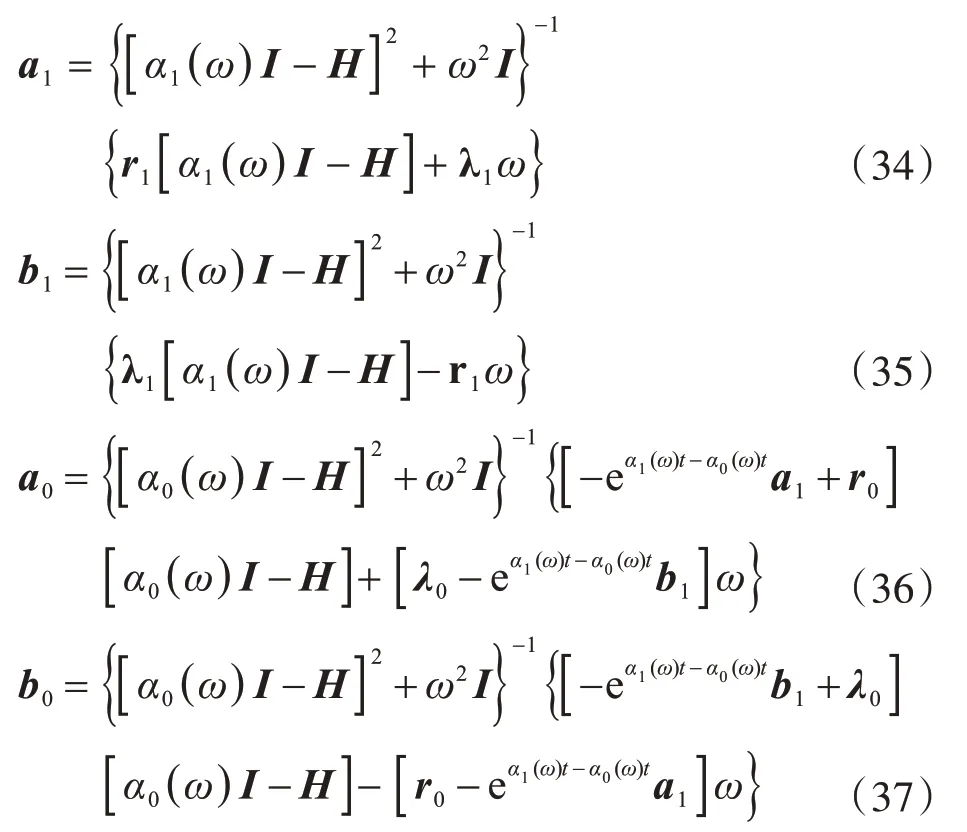
令t=tk+1代入式（29）就得到積分步長(zhǎng)終點(diǎn)處的狀態(tài)：

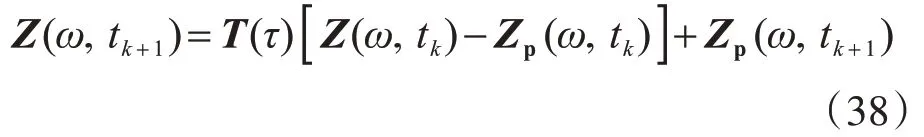
將式（33）代入式（38）即得精細(xì)積分較一般精確格式：

由式（22）和式（39），可以得到地震激勵(lì)x¨g的響應(yīng)為z(ω，t)，那么該響應(yīng)的自譜密度及方差可表示為

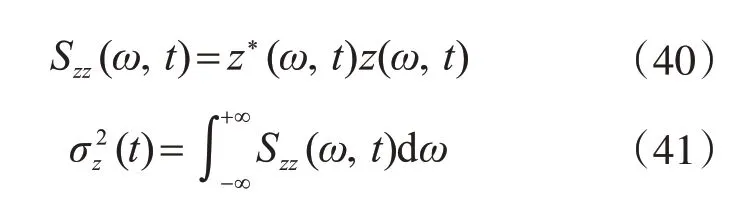
式中，*表示復(fù)共軛。

綜上步驟，設(shè)置支撐的廣義Maxwell 阻尼耗能結(jié)構(gòu)的位移、速度，阻尼器受力等非均勻非平穩(wěn)地震響應(yīng)均可得到。

4 算 例

如圖4 所示，設(shè)置支撐的五參數(shù)Maxwell 阻尼器單自由度減震系統(tǒng)，其結(jié)構(gòu)的基本參數(shù)為：質(zhì)量m=42 500 kg，剛度k=145.43×105N/m，阻尼比s0分別取0.02、0.04、0.08、0.20。Maxwell阻尼器的基本參數(shù)為：平衡剛度k0=0.36×105N/m，支撐剛度kb=1.5k，Maxwell阻尼器兩分支單元的剛度和阻尼分別為k1=42.08×105N/m，c1=0.83×105N·s/m；k2=6.87×105N/m，c2=2.15×105N·s/m。

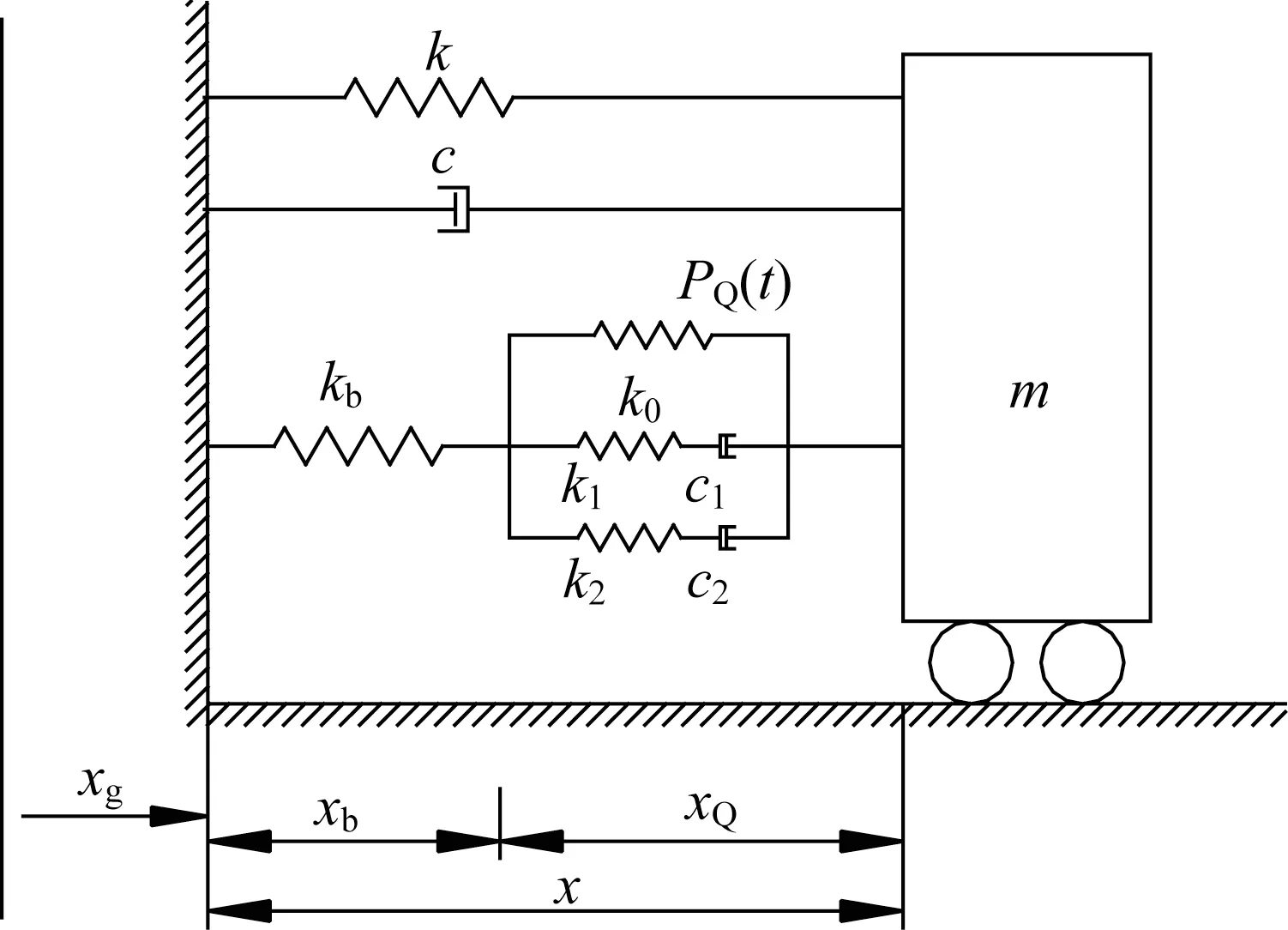
圖4 結(jié)構(gòu)計(jì)算簡(jiǎn)圖Fig.4 Structure calculation diagram

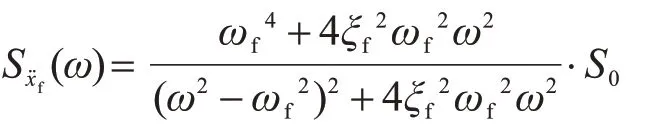
其計(jì)算取值為：ωf=19 rad/s，ξf=0.65；S0=0.015 54 m2/s3。

調(diào)幅函數(shù)分別取為Shinozuka-Sato 型［20］均勻調(diào)幅和Spanos-Solomos 型［21］非均勻調(diào)幅，計(jì)算參數(shù)分別取為

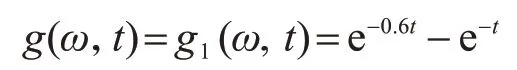
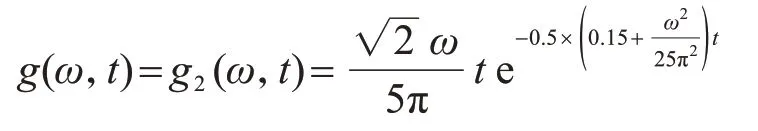
首先，運(yùn)用本文方法得到Shinozuka-Sato 型均勻調(diào)制非平穩(wěn)地震激勵(lì)作用下結(jié)構(gòu)響應(yīng)方差；然后，與精確解［22］進(jìn)行對(duì)比，驗(yàn)證本文方法的正確性與可行性，如圖5-圖10所示；最后，進(jìn)一步應(yīng)用到Spanos-Solomos 型非均勻調(diào)制非平穩(wěn)地震激勵(lì)作用下結(jié)構(gòu)響應(yīng)方差，如圖11-圖13 所示。可以看出：在非平穩(wěn)激勵(lì)下，結(jié)構(gòu)的位移、速度和阻尼器受力均具有峰值效應(yīng)，表現(xiàn)出明顯的非平穩(wěn)隨機(jī)特性，符合工程實(shí)際。

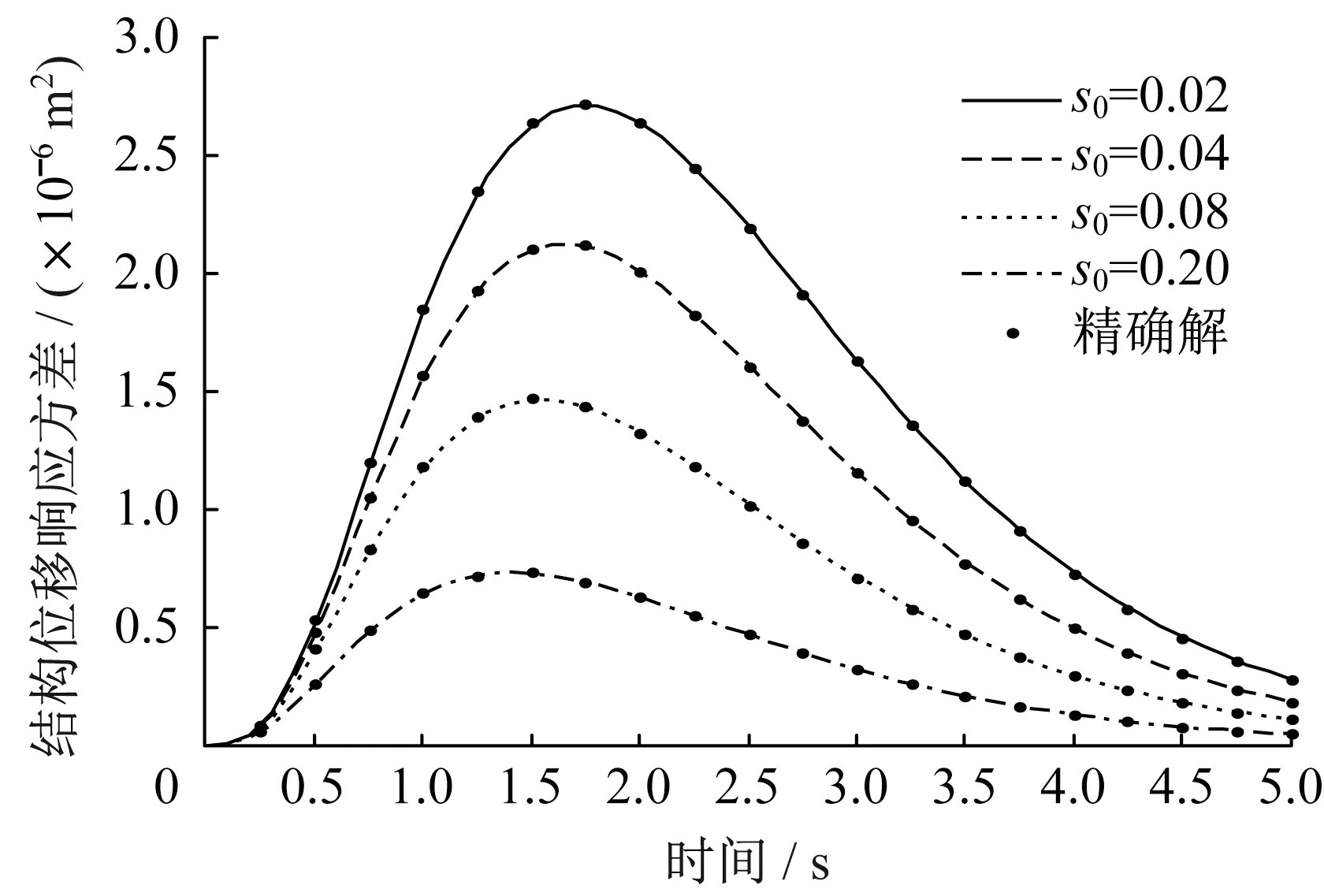
圖5 位移響應(yīng)方差Fig.5 Displacement response variance

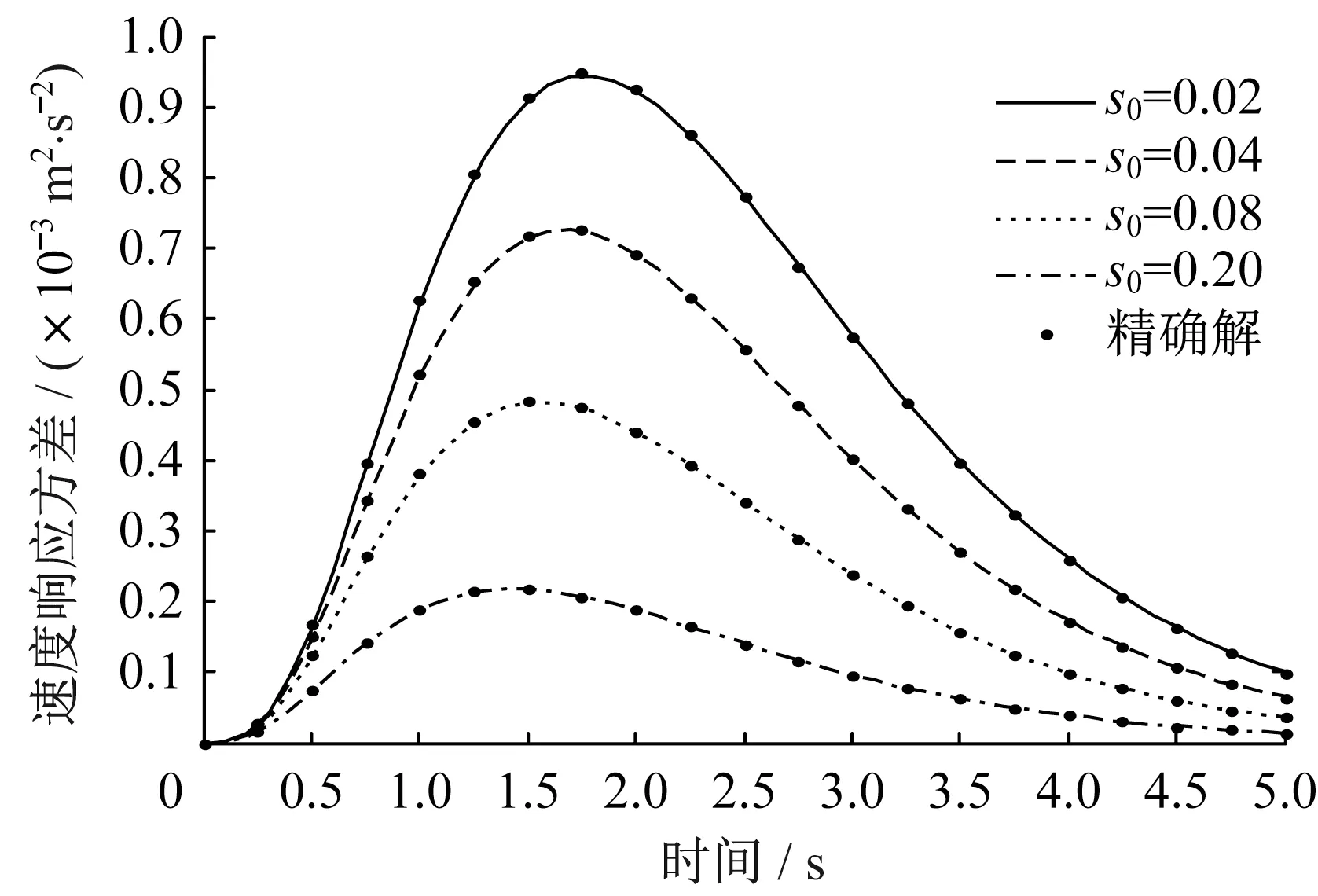
圖6 速度響應(yīng)方差Fig.6 Speed response variance

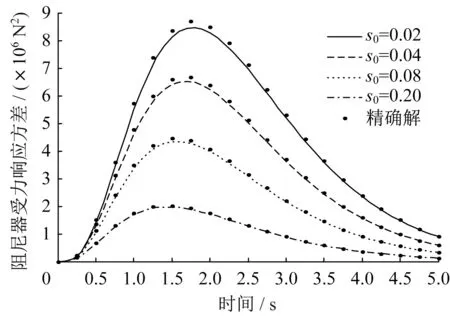
圖7 阻尼器受力響應(yīng)方差Fig.7 Stress response variance of damper

圖8 位移響應(yīng)方差Fig.8 Displacement response variance

圖9 速度響應(yīng)方差Fig.9 Speed response variance

圖10 阻尼器受力響應(yīng)方差Fig.10 Stress response variance of damper

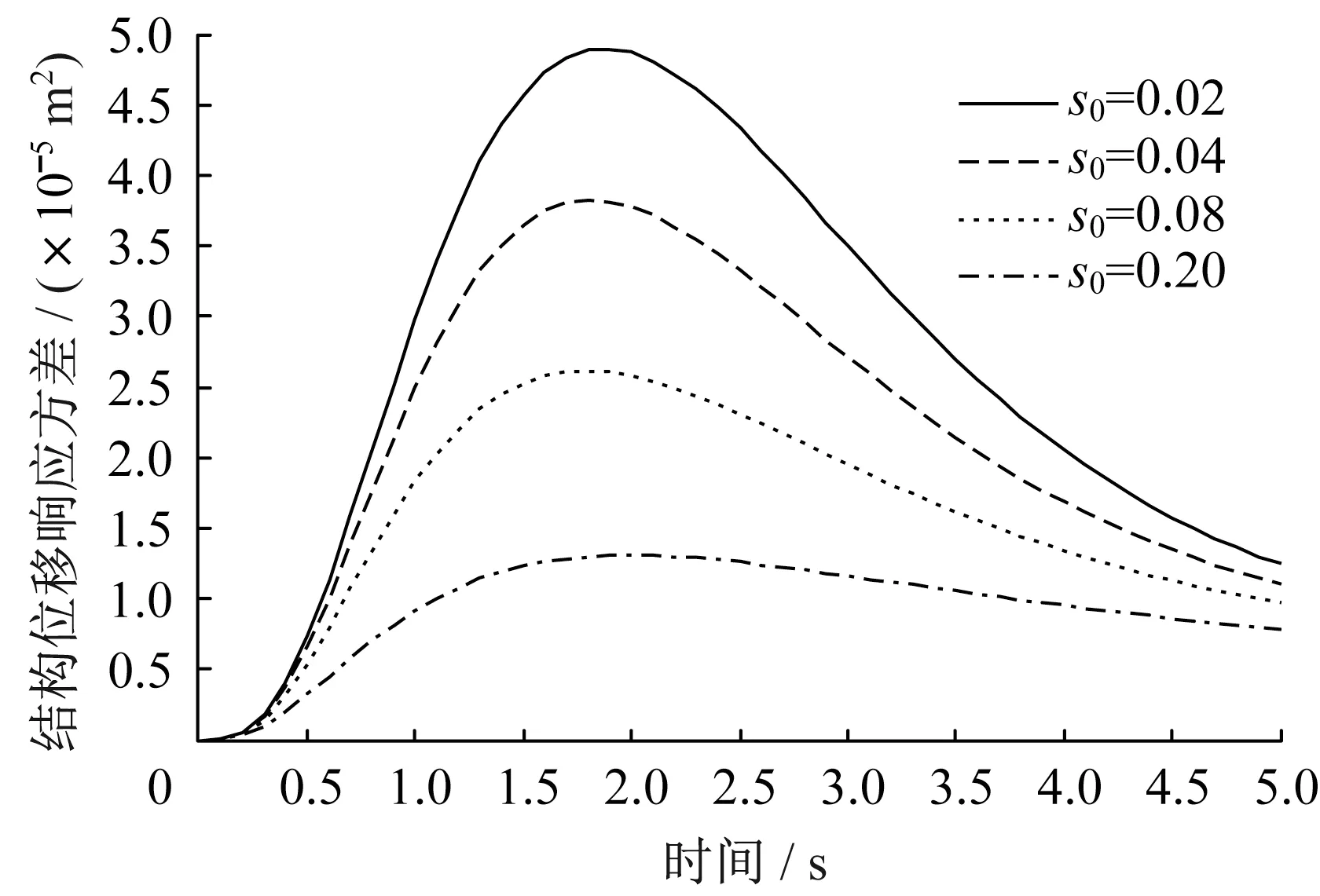
圖11 位移響應(yīng)方差Fig.11 Displacement response variance

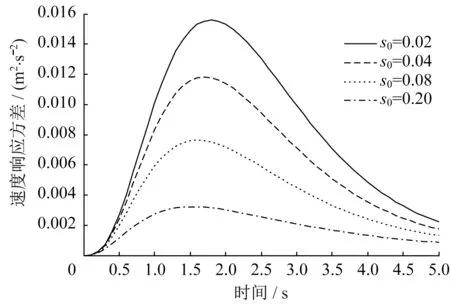
圖12 速度響應(yīng)方差Fig.12 Speed response variance

圖13 阻尼器受力響應(yīng)方差Fig.13 Stress response variance of damper

為了研究阻尼比對(duì)結(jié)構(gòu)響應(yīng)的影響，s0分別取0.02、0.04、0.08、0.20。阻尼比對(duì)結(jié)構(gòu)響應(yīng)的影響較大，在兩類非平穩(wěn)激勵(lì)下，三種響應(yīng)如圖5-圖7和11-圖13所示。阻尼比越大，響應(yīng)越早達(dá)到峰值，結(jié)構(gòu)的位移、速度和阻尼器受力響應(yīng)方差均越小。

為了研究支撐剛度對(duì)結(jié)構(gòu)響應(yīng)的影響，結(jié)構(gòu)基本參數(shù)不變，而rb分別為0.5、1.2、10、∞，支撐剛度kb=rbk，rb為支撐剛度與結(jié)構(gòu)剛度的比值，阻尼比取s0=0.1，在兩類非平穩(wěn)激勵(lì)下，三種響應(yīng)如圖8-圖10 和14-圖16 所示。支撐剛度對(duì)結(jié)構(gòu)響應(yīng)影響較大，響應(yīng)峰值發(fā)生時(shí)間不隨支撐剛度變化而變化，支撐剛度越大，結(jié)構(gòu)的位移、速度響應(yīng)方差越小，阻尼器受力響應(yīng)方差越大。

為確保阻尼器取得較好的減震效果，支撐剛度應(yīng)取kb≥10k，此時(shí)可按kb=∞情況下進(jìn)行近似計(jì)算；對(duì)于kb較小的情況，不能按kb=∞情況進(jìn)行近似計(jì)算，應(yīng)按kb的實(shí)際剛度進(jìn)行計(jì)算，否則將會(huì)導(dǎo)致錯(cuò)誤結(jié)果。

5 結(jié) 論

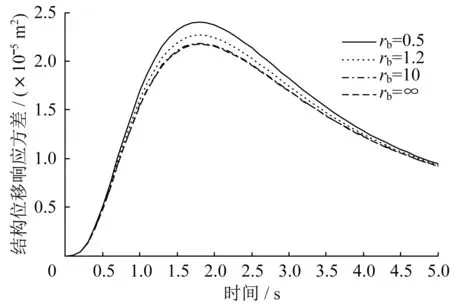
圖14 位移響應(yīng)方差Fig.14 Displacement response variance

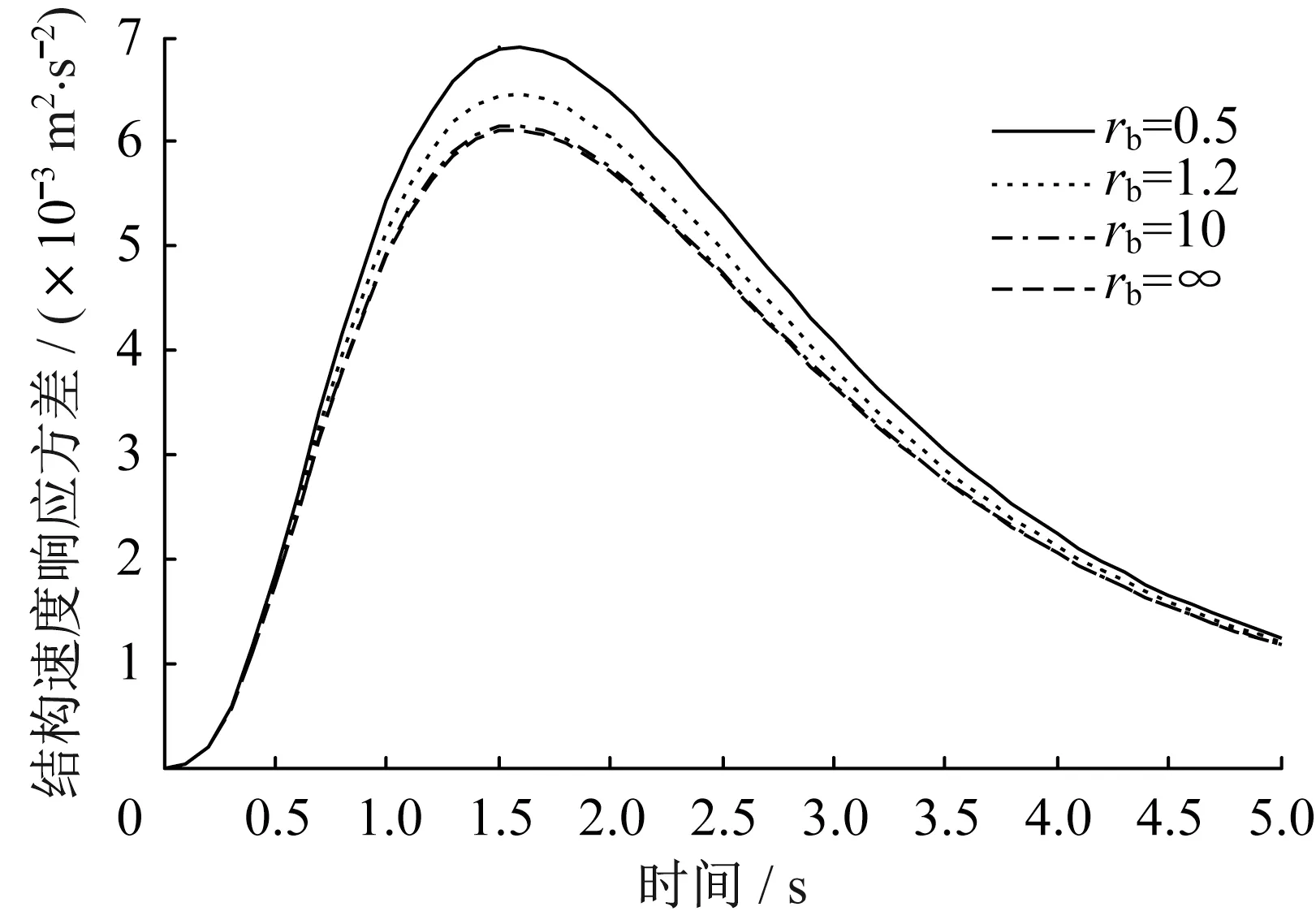
圖15 速度響應(yīng)方差Fig.15 Speed response variance

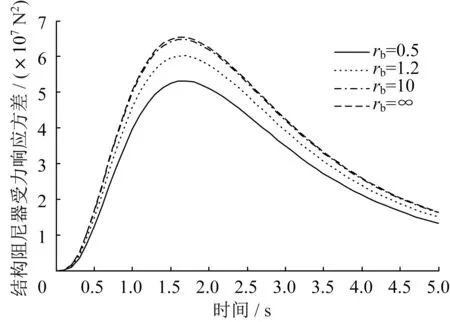
圖16 阻尼器受力響應(yīng)方差Fig.16 Stress response variance of damper

（1）為建立黏彈性耗能結(jié)構(gòu)及其保護(hù)系統(tǒng)的抗震分析與設(shè)計(jì)方法，本文將虛擬激勵(lì)法引入黏彈性耗能阻尼系統(tǒng)，獲得了非均勻精細(xì)積分較一般精確格式，得到了廣義Maxwell 阻尼耗能系統(tǒng)的均勻與非均勻非平穩(wěn)地震響應(yīng)方差。

（2）通過算例，驗(yàn)證了本文方法的正確性與可行性，該方法適應(yīng)于設(shè)置支撐的廣義Maxwell阻尼系統(tǒng)的非均勻非平穩(wěn)響應(yīng)分析，可直接應(yīng)用于黏彈性阻尼耗能系統(tǒng)響應(yīng)分析。

（3）支撐剛度對(duì)黏彈性耗能系統(tǒng)有重要影響，在支撐剛度較耗能系統(tǒng)剛度很大情況下，支撐剛度對(duì)耗能系統(tǒng)響應(yīng)的影響效果不再增加，一般情況下，應(yīng)考慮有限支撐剛度對(duì)耗能系統(tǒng)響應(yīng)的影響。

（4）盡管本文研究對(duì)象是單自由度結(jié)構(gòu)系統(tǒng)，但對(duì)于多自由度耗能結(jié)構(gòu)體系也可化為文中式（27）的形式，因此該方法同樣可應(yīng)用于多自由度設(shè)置支撐的廣義Maxwell 阻尼耗能系統(tǒng)非均勻非平穩(wěn)地震響應(yīng)分析，為非均勻非平穩(wěn)地震激勵(lì)下結(jié)構(gòu)系統(tǒng)及各減震構(gòu)件的響應(yīng)分析和抗震動(dòng)力可靠度分析提供了參考。