雙向張弦梁結構振動模態特性分析

徐蒙越 張 莉

（上海大學土木工程系，上海200444）

0 引 言

張弦梁結構在近20 年內發展迅速，是一類由上弦受壓彎剛性構件，下弦受拉的柔性鋼索，中間連以受壓撐桿形成的混合結構體系。該結構受力合理，結構效率高，因而受到了建筑師的青睞，在很多工程中得到了應用，例如上海浦東國際機場候機樓［1］、廣州國際會展中心［2］、哈爾濱國際體育會展中心［3］等。這些結構多采用多榀結構尺寸相同的張弦梁平行布置成屋面結構。

平面張弦梁結構受力合理，在初始態與受荷態幾乎沒有水平支反力，是一種比較理想的結構體系。該結構目前應用較多，富秋實提出了優化后的分段平面張弦梁結構［4］，性能更優。但平面張弦梁結構平面外剛度較差，為改善這一缺點，發展了雙向和多向張弦梁結構［5-6］。

張志宏等［7］基于計算參考構形，對平面張弦梁的計算分析理論等問題進行了討論。劉開國［8］針對雙向張弦梁結構提出了一種基于連續化假定的簡化算法。目前雙向張弦梁結構的動力特性分析仍然缺乏較為精確的計算方法。而模態分析作為結構動力特性研究的基礎，本文結合有限元算例對張弦梁結構的自振模態特性進行參數分析，研究了張弦梁結構的基本模態特性。

1 結構自振特性計算假定及步驟

1.1 計算假定

雙向張弦梁結構的模態特性計算采用以下基本假定：

（1）上弦所有節點均為剛接，梁單元為兩節點三維彈性梁；下弦所有節點均為鉸接，索單元為兩節點三維桿單元。

（2）結構邊界為鉸接邊界，一端節點約束三個方向的位移，另一端則僅約束豎向位移。

（3）結構始終處于彈性狀態。

（4）荷載作用簡化為等效節點質量，具體采用質量單元法。

1.2 計算步驟

雙向張弦梁結構的模態特性有限元分析步驟如下：

（1）設定結構零狀態坐標，對雙向張弦梁結構進行參數化建模，采用初應變法將預應力施加在下弦拉索上。

（2）打開大變形效應與非線性效應，進行非線性有限元分析，求解結構初始態。

（3）采用質量單元法編制宏文件將面荷載轉化為等效節點質量，并施加在初始態的模型相應節點上。

（4）采用Block Lanczos 法對結構進行模態分析，輸出結構自振頻率及振型參與系數等結果。

2 張弦梁結構自振特性

2.1 工程算例

算例為矩形雙向張弦梁結構，模型如圖1 所示，平面為邊長40 m的正方形，上下弦曲面均為拋物面，矢跨比與垂跨比分別為1/25與1/20。上弦梁為300×600×8×15 的 方 鋼 管，彈 性 模 量E=2.1×1011N/m2；中間撐桿為φ120× 6 圓鋼管，彈性模量E=2.1×1011N/m2；下弦拉索均為φ5×55 鋼絲束，彈性模量E=1.9×1011N/m2。計算考慮自重作用，鋼材密度為7 850 kg/m3。上弦梁與撐桿選用Q345 鋼材；下弦索材料極限抗拉強度為1 770 N/mm2，設計安全系數為3，應力限值［σ］=590 N/mm2。圖1 中邊界x=0與y=0節點約束三個方向的位移，另一端僅約束豎向位移，用以模擬實際工程中一端固定鉸支座另一端滑動鉸支座［10］。采用初應變法施加在全體下弦索單元上，預拉力P取值為300 kN，初應變具體計算如下：

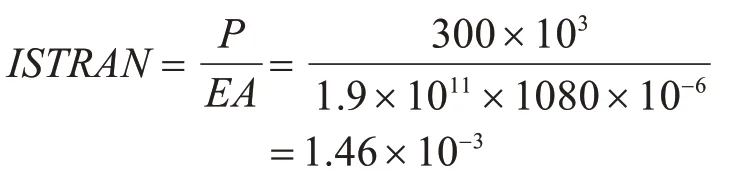
屋面恒荷載為0.5 kN/m2，活荷載為1.0 kN/m2，設計工況為1.2×全跨恒荷載+1.4×全跨活荷載。

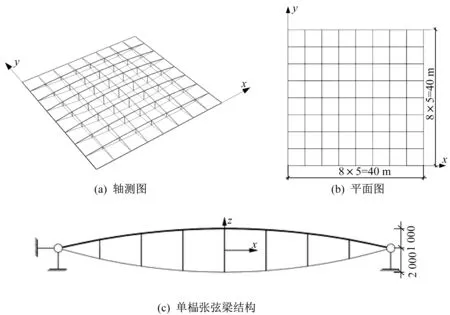
圖1 模型簡圖Fig.1 Model sketch

2.2 分析結果

表1 為頻率與模態參與系數。表中小于10-4的量均認為約等于零，rx，ry，rz依次為x，y，z 方向振型貢獻率，MFx，MFy，MFz依次為x，y，z方向累計質量分數，ri為第i階振型貢獻率。

表1 結果表明，雙向張弦梁結構的自振特性有以下特點：

（1）雙向張弦梁結構以曲面水平方向振動為主，觀察算例模型的前20 階振型，x 與y 方向模態質量參與比例達70 %以上，z 向模態質量參與比例僅11.13%。本文認為算例模型的自振特性表現是受邊界條件影響的結果，即在雙向張弦梁結構的一端僅約束豎向位移，導致水平方向的模態質量參與比率遠高于z向的模態質量參與比率。

（2）如表1 所示，雙向張弦梁結構基頻較高，說明該結構具有較好的結構剛度。振型分布較為稀疏，在一定范圍呈較小的臺階型分布，算例中第1 階與第2 階自振頻率差值為0.092 9 Hz，第9 階與10 階自振頻率差值為0.174 4 Hz，第15 階與第16 階自振頻率差值為0.086 9 Hz，第18 階與第19階自振頻率差值為0.075 Hz。同時算例的基本周期為0.044 s，也表明該結構具有良好的結構剛度。

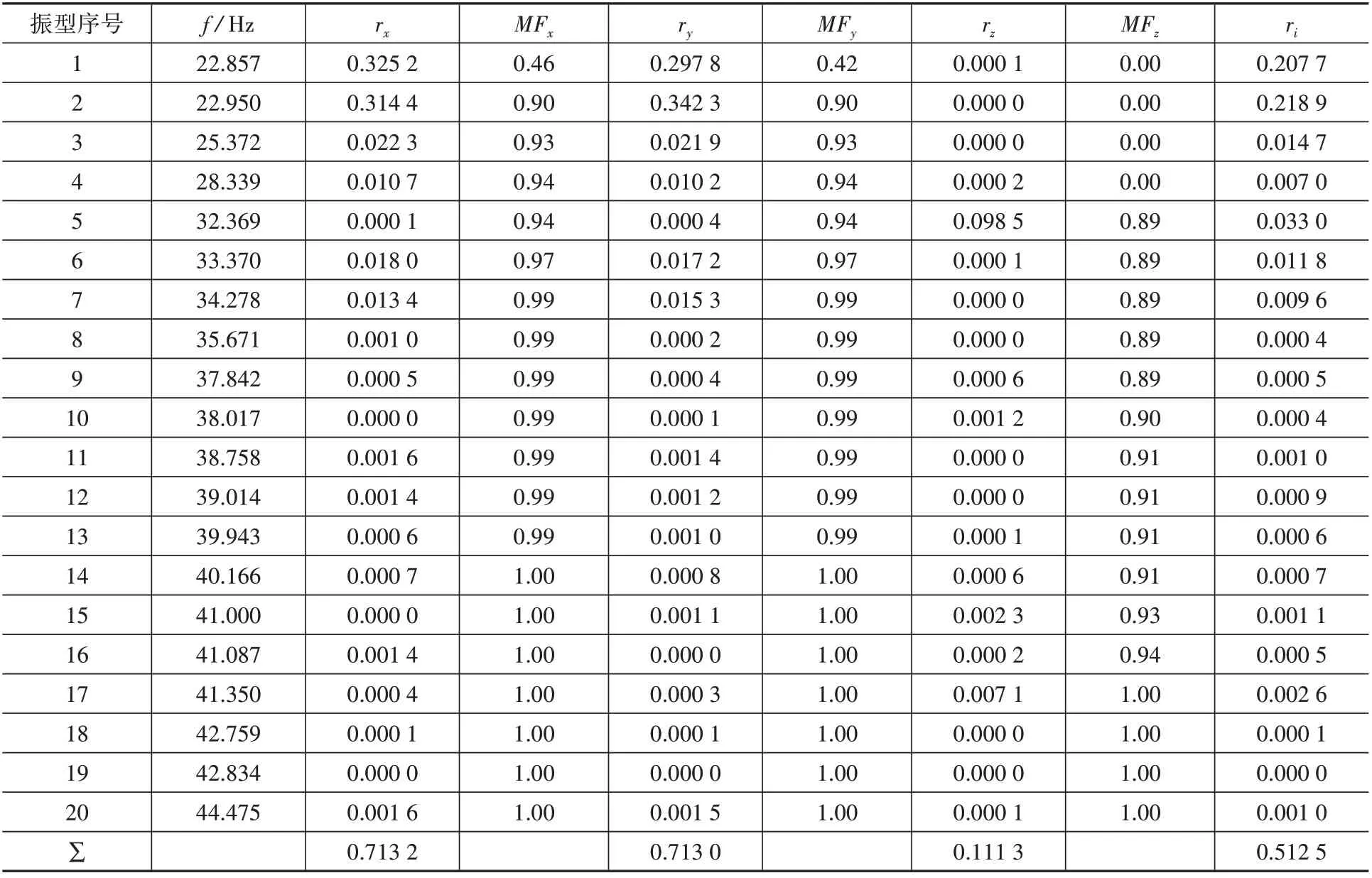
表1 頻率與模態參與系數Table 1 Frequency and modal participation ratio

（3）由于邊界條件的緣故，振型表現沿y=x軸線呈正對稱與反對稱。前6 階振型中1、3、6 階振型呈反對稱，2、4、5 階振型呈正對稱，其中第5 階振型較為特殊，水平振型貢獻幾乎為0。同時也可以看出，模態擴展階次的確定是一個重要環節。前20 階累計振型貢獻率為0.512 5，且x、y 與z 方向累計質量分數均達到了99%以上。因此本文建議，利用反應譜分析雙向張弦梁結構抗震能力時，至少應采用前17階振型。

為直觀計，圖2給出了算例模型前6階振型。

3 結構振動模態參數分析

由無阻尼結構自由振動方程可得，結構模態特性由結構質量和剛度共同決定。而影響雙向張弦梁結構剛度的因素主要有下弦拉索預應力、上弦曲面矢跨比和下弦曲面垂跨比等。由于雙向張弦梁結構是由三種不同受力性質構件組合而成的混合結構，其剛度受到多種因素影響，結構響應對不同參數變化的敏感性也不盡相同。

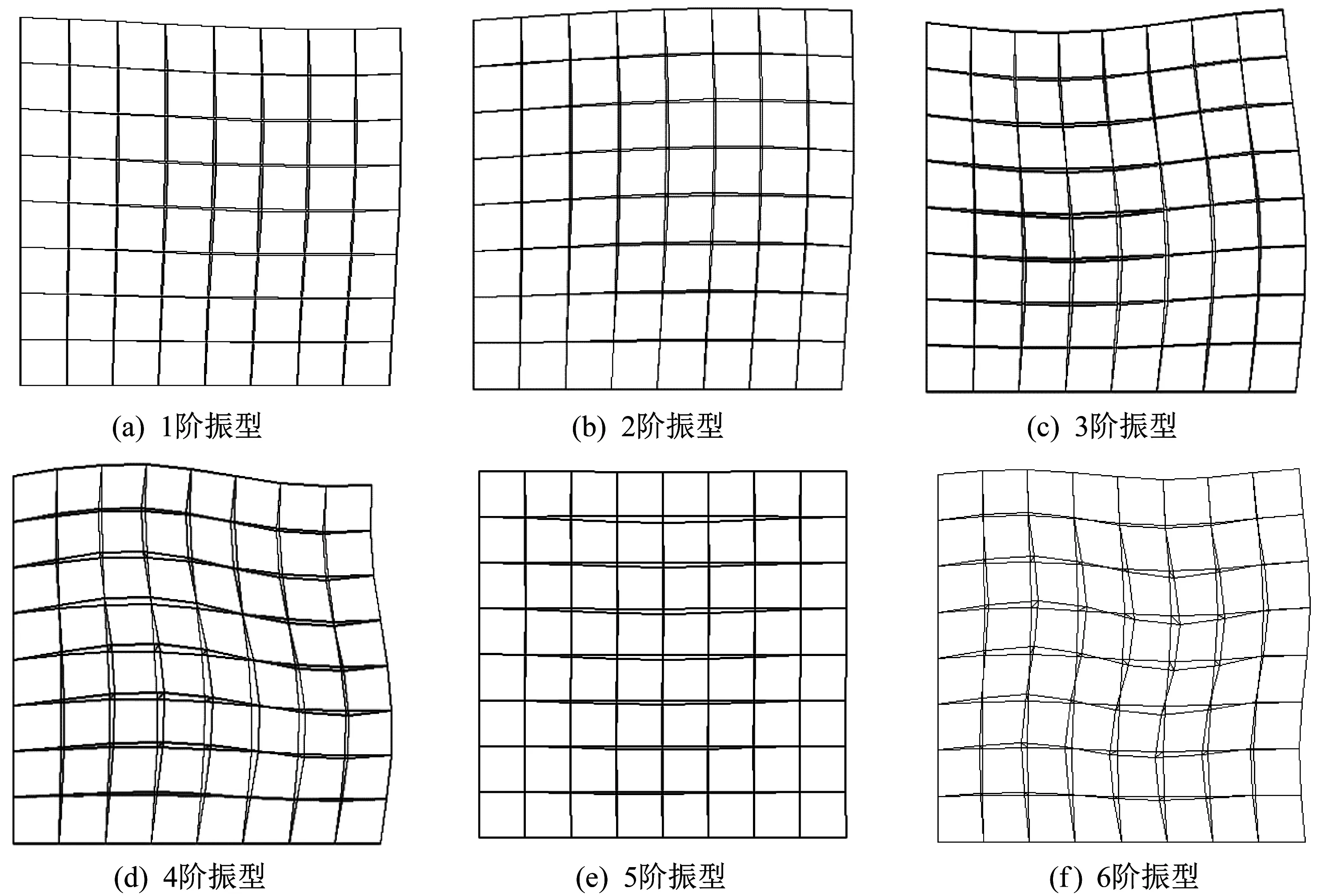
圖2 1～6階振型圖Fig.2 The first 6 vibration modes

表2-表5給出了考慮大變形效應雙向張弦梁結構模態特性隨各參數變化的計算結果。

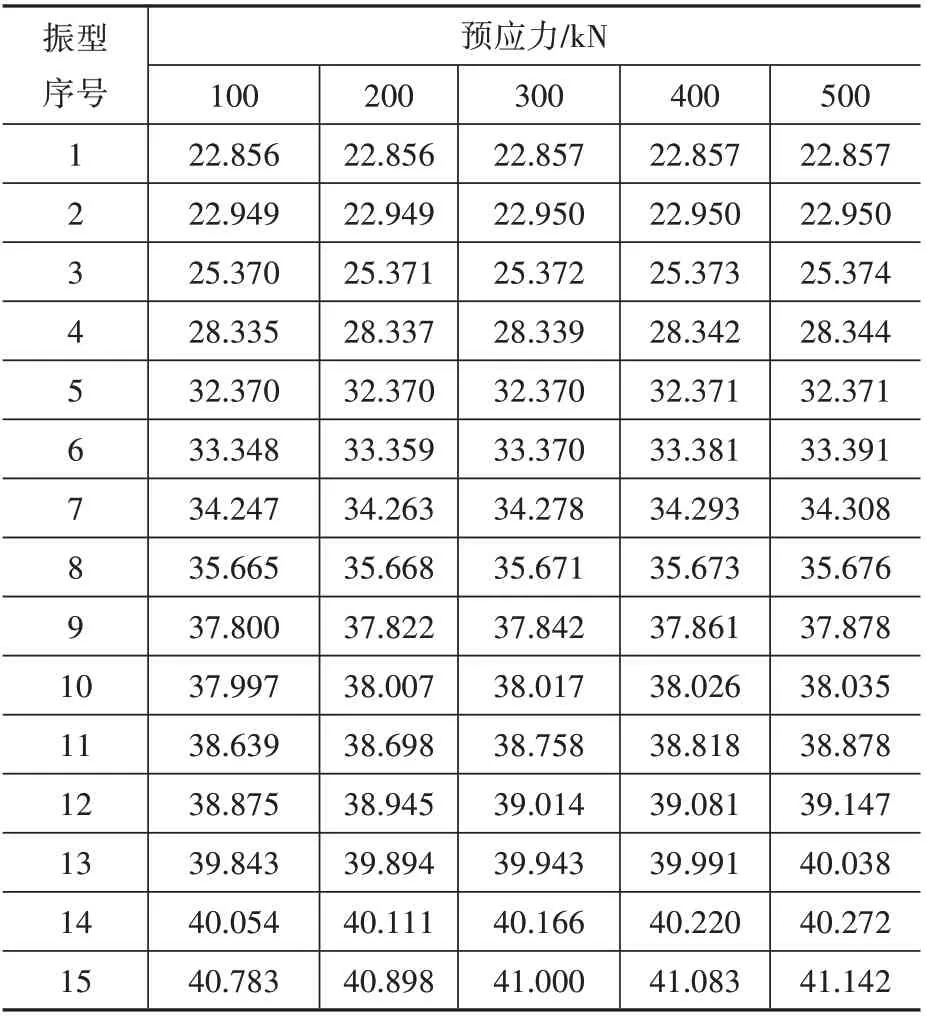
表2 預應力變化下的自振頻率Table 2 Natural frequency in the case of the variation of prestress

由表2 可見雙向張弦梁結構的低階自振頻率（1-5 階）隨預應力的增大，略微增大，但增長的幅度很小；高階頻率（6-15 階）隨預應力增大而明顯增大，但增大幅度隨預應力增大而略有下降。表2 中所表示的預應力為零狀態時施加的預應力，經過初始形態分析計算，此預應力值明顯大于初始態下弦索的軸力。考慮充分利用結構的性能與初始形態上弦曲面位移限值，雙向張弦梁結構上弦一般選擇剛度大截面小的構件，這也導致預應力對雙向張弦梁結構自振頻率影響較小。

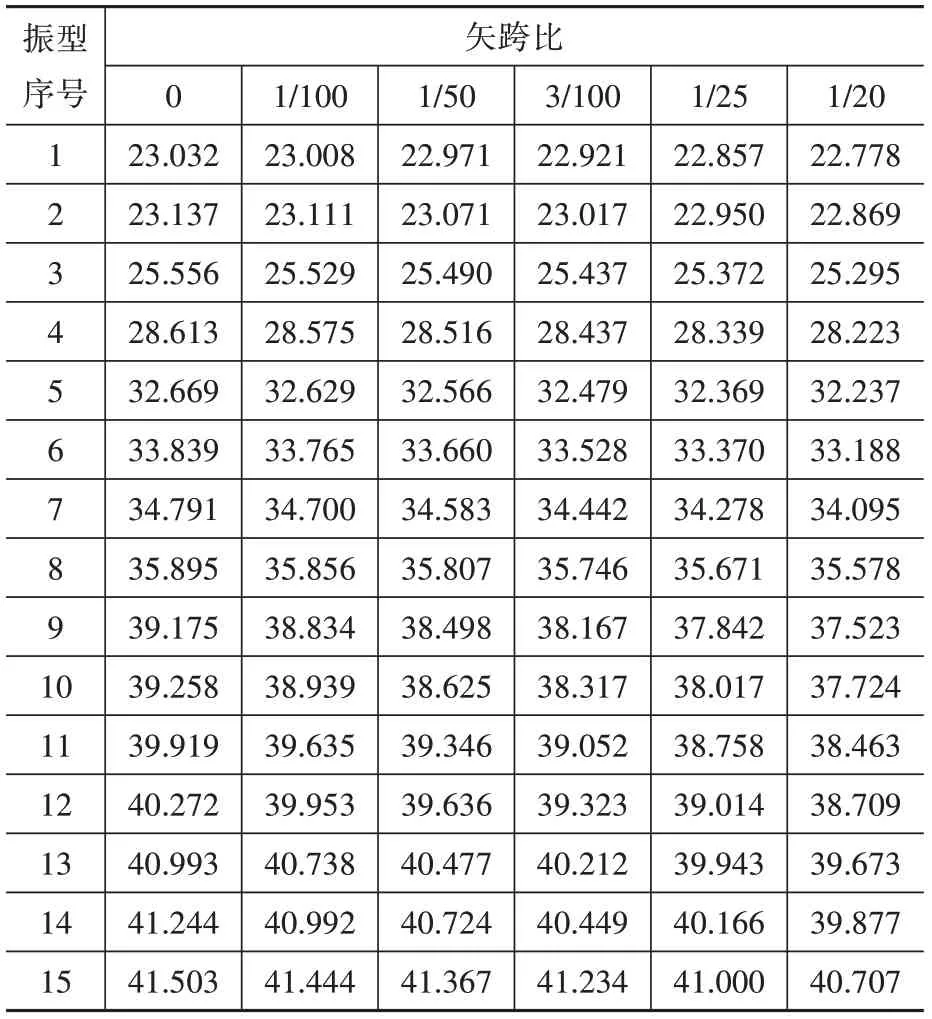
表3 矢跨比參數變化下的自振頻率Table 3 Natural frequency in the case of the variation of rise-span ratio

表3 與表4 分別為矢跨比與垂跨比參數變化下雙向張弦梁結構自振頻率數據。隨著矢跨比與垂跨比的增大，結構自振頻率隨之減小，結構剛度降低。表3 中矢跨比變化范圍為0/40～2/40，垂跨比變化范圍為1/40～3/40，相應的自振頻率變化最大差值均出現在9 階，分別為1.652 與2.640，前15階平均值分別為0.864與1.148。數據表明相比于矢跨比參數變化，雙向張弦梁結構自振頻率對垂跨比參數變化更為敏感。

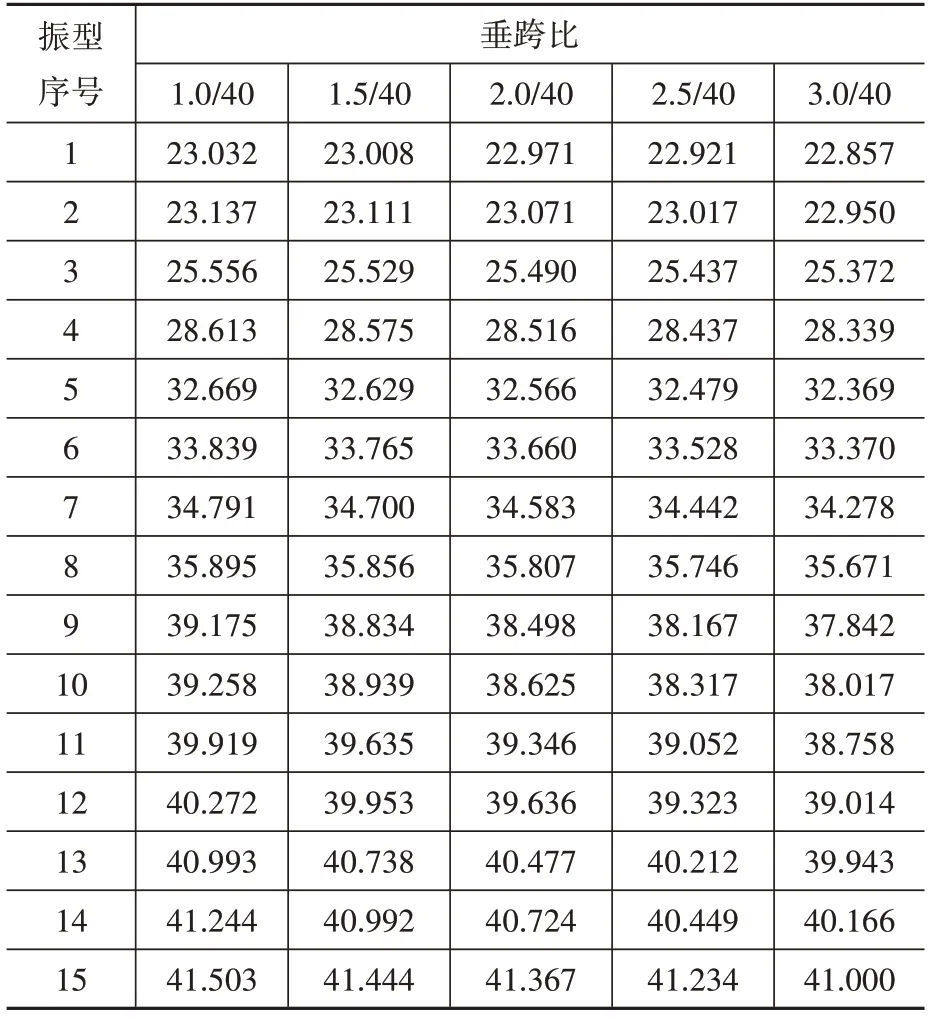
表4 垂跨比參數變化下的自振頻率Table 4 Natural frequency in the case of the variation of sag-span ratio

表5 表明，雙向張弦梁結構自振頻率隨節點質量的增大而減小，其中高階頻率的減小幅度明顯大于低階頻率的減小幅度。但對于相同階數的自振頻率，隨質量增大，自振頻率減小幅度減小。

總體而言，節點質量通過對雙向張弦梁結構質量矩陣的改變進而對結構自振頻率產生影響，且敏感性最高。預應力、矢跨比與垂跨比通過對結構的剛度矩陣的改變進而對結構自振頻率產生影響，其中矢跨比與垂跨比參數影響較為顯著，預應力參數的影響較弱。

4 結 論

通過本文中的上述分析，可以對雙向張弦梁結構的自振特性得出以下結論：

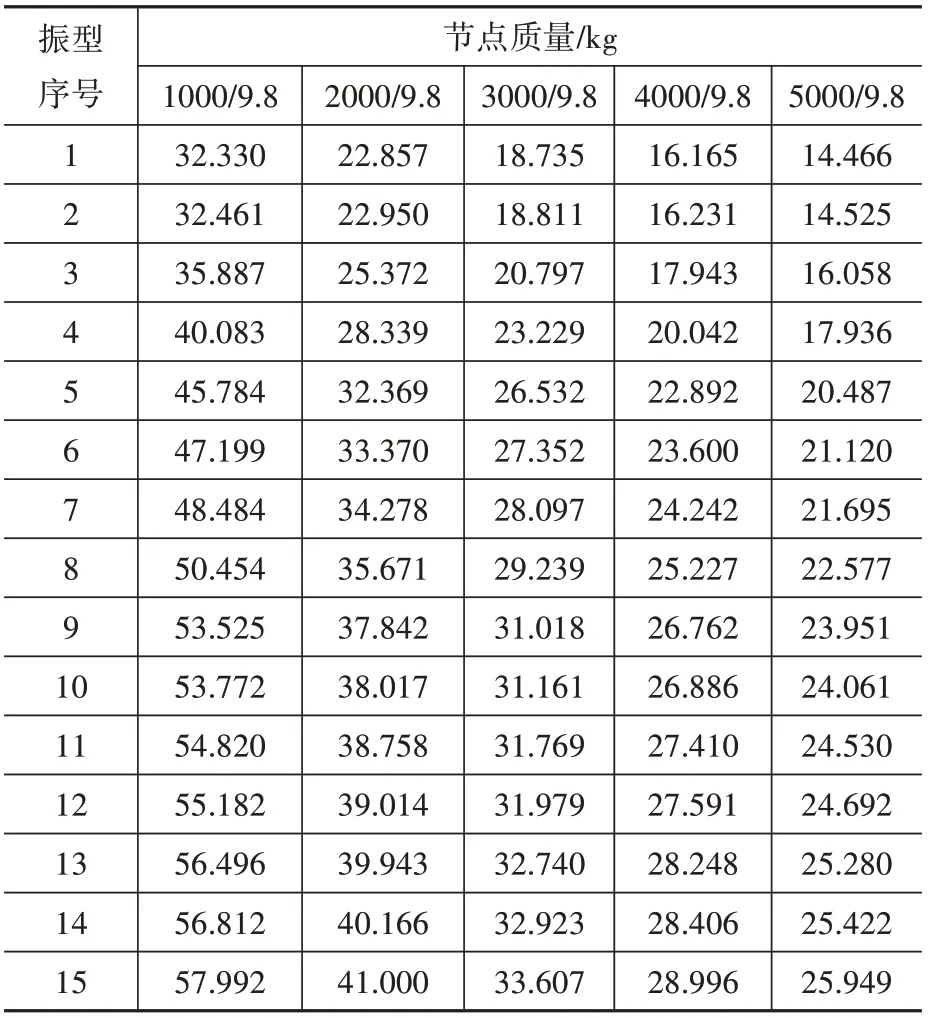
表5 節點質量變化下的自振頻率Table 5 Natural frequency in the case of the variation of structure mass

（1）雙向張弦梁結構自振頻率分布較為稀疏，存在部分階數的自振頻率十分接近的情況，基頻較高，自振周期較短，結構具有良好的剛性。

（2）同時受到邊界條件的影響，振型以水平方向振動為主，水平方向的模態質量參與比率遠高于豎向的模態質量參與比率。

（3）參數敏感性方面，雙向張弦梁結構自振頻率對于節點質量參數敏感性最高，對于矢跨比與垂跨比參數敏感性一般，對于預應力參數敏感性較低。