生長激素內分泌調節的模型及混沌行為研究

巴合提古麗·阿斯里別克，張文雅，吐爾遜·艾迪力比克，孫迎春

(1.伊犁師范大學電子與信息工程學院光電材料與器件實驗室，新疆 伊寧 835000；2.中國人民解放軍聯勤保障部隊第九六四醫院，吉林 長春 130062；3.東北師范大學物理學院，吉林 長春 130024)

0 引言

生長激素(growth hormone，GH)是人體生長發育的重要因素之一，它在體內的分泌釋放受多重因子的調節，但直接的來源是腺垂體生長激素細胞.諾貝爾醫學獎獲得者John Gurdon指出，人體身高由核心軸生長軸及合成代謝軸、生長神經軸、內分泌軸、下丘腦垂體軸、長骨生長軸等相關因素決定，能有效解決增高的方法只有“生長軸重組體系”[1].可見，生長激素在促進人體的生長發育中是起極其重要的作用.從組織和分子水平上說，生長激素促進了構成各種組織的分子及蛋白質的合成，促進骨及骨關節等的生成[2-3].研究人員很早就發現，人幼年期如GH分泌不足，會出現生長停滯、個子矮小的現象，嚴重者會出現侏儒癥等病癥；GH分泌過多，則會導致生長過快，甚至出現巨人癥和肢端肥大癥等[4-6].

生長激素及其相關調節因子的作用在生理學上已很明確，其調節循環主要依賴于神經內分泌生長系統，在生長發育的相關理論中稱之為神經內分泌生長軸，簡稱生長軸.該系統主要是由下丘腦、垂體、靶腺的一系列激素及受體構成[7].系統內激素的分泌具有明顯的節律性，比如：青春前期和青春期的青少年24 h內生長激素脈沖數6～8次，平均3～4次，并具有夜間分泌量及頻率都比白天多的規律，在深睡后1 h左右，生長激素分泌最旺盛，可達50～60 μg/L[8]，因此，想長高的孩子要保證充足且高質量的睡眠.此外，其在血液中濃度還有1～3 h脈沖式釋放的節律[9-10]，這種具有節律的現象在地球上是普遍存在的，最典型的例子之一就是晝夜節律及伴隨而來周期性的覺醒與睡眠.實際上，太陽、月亮的運動規律直接導致了地球上生物的節律性變化，違反這種自然的節律會引起人的機體功能混亂、情緒煩躁、工作效率降低等現象[11-12].有關生物節律的研究早已成為了許多學科領域的研究熱點[13-15]，尤其是分子水平發現的節律控制機制，揭開了生物節律的奧秘，得到了科學界的普遍認可[16-19].

目前，非線性科學在各個領域得到了廣泛的應用[20-22]，比如在神經網絡系統、保密系統、生命科學等方面的應用都獲得了很好的效果，已成為新的研究熱點[23-27].因此，本文采用非線性的理論和方法，結合生理學和酶促反應動力學等理論，對人體生長系統中的激素分泌進行建模研究，從而揭示生長激素內分泌調節的行為和規律.

1 模型的構建

1.1 生長激素內分泌調節機制及簡化框圖

下丘腦-垂體-靶細胞軸的作用主要是通過控制人體各個靶器官激素的分泌，來調節人體的生長發育等功能.其分泌的激素主要包括生長激素、糖皮質激素、甲狀腺素、性腺激素等.神經內分泌生長軸是其中的一個分支，它有刺激和抑制兩方面的通路.它的刺激生成路徑：首先由下丘腦中的神經元分泌生長激素釋放激素(Growth Hormone Releasing Hormone，GHRH)，然后，GHRH與其受體結合，促進了垂體釋放出GH激素，GH又刺激肝臟等外周器官和組織來分泌類胰島素生長因子(Insulin-like Growth，IGFs)，并借助IGFs實現對機體生長發育的調控作用.它的反饋循環路徑主要有兩方面：一是血液中過高濃度的GH通過垂體門脈血管逆流，激發了生長激素釋放抑制激素(Growth Hormone-releasing Inhibitory Hormone，GHIH)的分泌，這直接對GHRH的分泌起到了抑制作用，即為負反饋，也稱之為短環反饋(short-loop feedback)；二是血液中的IGFs也間接抑制GHRH的生成，從而抑制了垂體細胞分泌GH.實驗表明，IGFs可在下丘腦和垂體兩個層面以負反饋機制來調節GH的分泌，由于GH分泌受控，反過來又影響了IGFs自身的分泌，這種反饋也稱之為長環反饋(long-loop feedback)[28-31].生長激素具有促進生長發育，影響糖、蛋白質、脂肪代謝的生理作用.通常運動、睡眠等外在因素，對GH的分泌也有一定影響，但其自發性分泌是始終存在的.正常情況下，GH的分泌具有晝夜節律性，且呈脈沖式.綜合以上分析，在忽略次要影響因素的情況下，可將生長軸系統各因素之間的正負反饋作用見圖1.

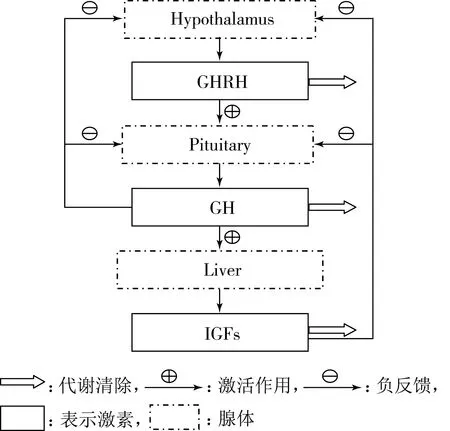
圖1 下丘腦-垂體-生長軸中各激素正負反饋模擬圖

1.2 神經內分泌生長軸激素分泌動力學模型

神經內分泌生長軸系統中，激素之間相互作用不是簡單的線性關系.已有的知識只停留在定性表示系統內部的調控是通過激素之間的相互協調完成的層面上，但缺少表示這些變量之間確切依賴和聯動關系的動力學分析.激素分泌隨時間變化的非線性動力學分析可解決以上問題，能全面展現此系統激素分泌的晝夜節律和激素間相互調控的精確依賴關系.

從分子水平上看，生物的生長發育及新陳代謝等都是酶催化下的酶促反應，因此符合酶促反應動力學理論[32].利用Michaelis-Menten定律及其推廣形式[33]，則體內激素的生成速率以分數形式成立，將生長軸內外周血中激素的濃度設為變量，即可建立此變量隨時間變化的微分方程組：

(1a)

(1b)

(1c)

式中：x1表示下丘腦神經元分泌的GHRH的血漿濃度(單位：μg/L)；x2表示腺垂體分泌的RH的血漿濃度(單位：μg/L)；x3表示肝臟等靶器官分泌的IGFs的血漿濃度(單位：μg/L)；t表示時間(單位：min)；λi表示機體對各個激素的代謝清除系數(Metabolic Clearance Rate，MCR)，是激素的自然代謝過程；ai(i=1，…，14)為正的常系數，其中：a2表示下丘腦神經元自主分泌(Autonomous Secretion)的激素，a1，a6，a12表示對應器官以外的激素分泌強度，比如，a1是下丘腦以外的釋放激素分泌源的分泌強度，也包括神經系統對生長激素釋放激素分泌的影響，其余的常系數表示激素間的相對作用強度.

在方程組(1)中，分子中出現的變量表示對自身的分泌有促進作用；分母中出現的變量則表示對自身的分泌起負反饋作用；當變量同時出現在分母與分子中時，則表示此激素自身具有飽和性.以方程(1a)為例，GHRH分泌過程呈現分數形式，表示出是復雜的酶促反應過程，分子中的x1表示GHRH對自身的分泌起刺激作用，分母中的變量x2和x3分別表示GH和IGFs對GHRH起著負反饋作用.依此類推，即構建出了神經內分泌生長軸激素分泌的非線性動力學方程.

方程組中表示的是各變量xi隨時間變化的動力學演化規律，由于其中分式的分母或分子的所有系數均為正，基于代數方程的理論可知，該方程組沒有實數的解析解，而xi表示激素在血液中的濃度，且都為正值，即實際模型分式的分子無極點，分母無奇點[34]，模型中分式不存在奇點發散的情形.分式具有非線性特征，它與清除項的共同作用，可以維持系統處于振蕩周期或混沌狀態.

2 模型方程組的求解與分析

為了求解方程組(1)中的17個待定常數，只能采取給予這些常數賦值后進行運算的試探法，即通過反復多次的試探和迭代去尋找合理的常系數.因此采用Matlab計算平臺，針對方程組(1)式進行編程和計算，從而獲得神經內分泌生長軸非線性動力學模型的數值解.

2.1 模型方程的周期振蕩解

首先依據臨床上實際測定的數據[35-36]，選取x1，x2，x3適當的初始條件(分別為0.1，1.2，220 μg/L)，在Matlab軟件中運用變步長四階龍格-庫塔法，并賦予模型方程組中的待定常系數為如下數值時，就獲得了神經內分泌生長軸激素分泌具有周期振蕩的行為方程組為：

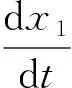
(2a)

(2b)

(2c)

模擬出的這組周期振蕩解的時域圖見圖2.從圖2中可以看出，x1，x2，x3的分泌隨時間都以均勻振蕩的形式出現，周期均為199.05 min，相應的振蕩峰值分別為0.33，1，248 μg/L，均在臨床測得值范圍之內[35-36].已有實驗證明[37]：GH的釋放呈脈沖式分泌狀態，每隔1～4 h出現一個脈沖，其脈沖式分泌正是由于GHRH的脈沖式分泌而決定的，GHRH無論在白天或夜晚成長激素皆呈脈沖式釋放，間隔3～5 h，脈沖期間的基礎值很低.從圖2明顯可見，各個激素的濃度呈周期性變化，說明激素的分泌的節律性，其振蕩幅值和周期大小均與實驗結果一致[35-36].

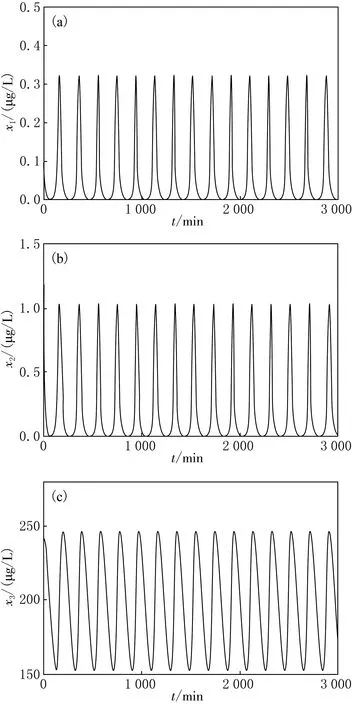
圖2 各個激素濃度隨時間演化的時域圖

為了進一步分析激素間分泌的遞進關系，通過運算將時域圖變換為激素間相互作用的相圖表示(見圖3).

(a)GHRH-GH；(b)GH-IGFs

由圖3可見，在經過初始暫態后，各激素相互關系形成了一個封閉的曲線，形成了一個循環的動力學過程.圖3(a)顯示，同一個x2值對應閉合曲線上的一大一小2個x1值，說明了系統中激素間分泌的正負反饋關系，處在正向進程中時，隨著x1的增加，x2也呈現增加狀態，但到達峰值后，則出現了負反饋進程，x2對x1的負反饋，使得x1分泌減少，進而又影響了x2的分泌，二者都呈現分泌下降的狀態.圖3(b)顯示，首先是x2和x3同時呈現增大狀態，達到峰值后，x2開始下降，但此時x3還在繼續增加，當x2下降到0.321 μg/L時，x3才開始下降，二者的正負反饋調節是有延遲的.

2.2 激素特征量的理論計算

2.2.1 各激素基礎值

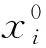
(3)

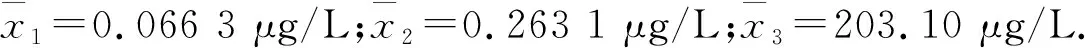
2.2.2 激素的代謝清除率MCR

方程組(1)中的λi表示激素的代謝清除系數，因此，MCR可寫成

MCRi=Viλi.

(4)

其中Vi是激素的分布體積，臨床上還很難準確給出它的準確值，但通常得到認可的是把Vi認定為人體的外周血的體積[38-39].不同的實驗和分析方法總是給出不同的Vi值，因此，使用文獻[38-40]的參數，即V1=V2=V3=5 L.這樣，由方程(4)可算得MCRi為：

MCR1=V1λ1=5×0.059 L/min=2.95 L/min=424.8 L/d；

MCR2=V2λ2=3.8×0.023 5 L/min=0.494 L/min=128.6 L/d；

MCR3=V3λ3=5×0.006 L/min=0.025 5 L/min=43.2 L/d.

2.2.3 激素的產生率

激素的產生率(Production Rate)即為單位時間內激素產生出的量值，應等于(2)式中的前

兩項取平均值再乘以各自的分布體積Vi來求得.因此，3種激素的產生率P分別為：

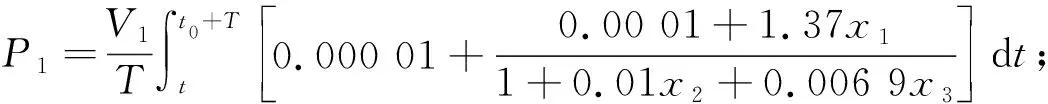
當V1=V2=V3=5 L時，分別可得到各激素產生率為：

P1=1.37×10-3μg/min=1.974 μg/d；

P2=5×10-3μg/min=7.2 μg/d；

P3=5.08 μg/min=7.32 μg/d.

2.2.4 激素半衰期

激素半衰期(用τi表示)可表示激素更新的速度，其與代謝清除有關，計算公式為

(5)

因λi(i=1，2，3)已算得，分別為0.058，0.023 5，0.006，因此

τ1=ln2/0.058=11.95 min；

τ2=ln2/0.023 5=29.5 min；

τ3=ln2/0.006=115.5 min.

可見，GHRH、GH、IGFs的半衰期逐漸增加，GHRH最短，說明其在下丘腦中生成后存在的時間最短，而IGFs最長，說明在外周器官中存在時間最長，接近2 h.

為了進一步檢驗理論模型的合理性，將理論計算值與實際臨床檢測值[33-36]進行一一對比(見表1)，發現激素的各個特征量都符合得很好，說明建立的理論模型是合理的.

表1 激素特征量的臨床測得值和理論計算值對比

3 激素的非線性分泌過程

3.1 模型方程的倍周期解

非線性系統的一種極為重要的運動形態就是混沌行為.地球上的各種生物是自然界最復雜的系統，在其各種運動變化中出現混沌狀態已被大量的事實和分析所證明[40].因此，神經生長軸內分泌調節的過程也不能是嚴格的周期行為，而應該是在限定范圍內具有一定變動的混沌行為.為了驗證這一點，對建立的模型做進一步的賦值計算，首先在基礎值附近選取初值，分別為：x10=0.007 μg/L，x20=0.04 μg/L，x30=7.5 μg/L，然后進行反復迭代，則在周期振蕩解的基礎上，得到了具有倍周期特征的解，即方程組為：

(6a)

(6b)

(6c)

求出方程組(6)數值解的時域圖(見圖4)，可見激素濃度經過短暫的暫態過程之后呈現出非周期振蕩狀態，與周期振蕩解類似，在1 000 min內，仍然具有5個激素分泌的峰值，之后再進行如此的循環，呈現出明顯一高一低的2倍周期變化特征.

圖4 各激素2倍周期分泌的時域圖

為進一步清楚顯示激素間的相互作用關系，做出2倍周期解的相圖表示見圖5.由圖5可見，經過一個暫態后，系統進入一大一小2圈的循環狀態，這2圈一直持續循環不重合，表明了系統從周期振蕩進入了倍周期的分叉過程.

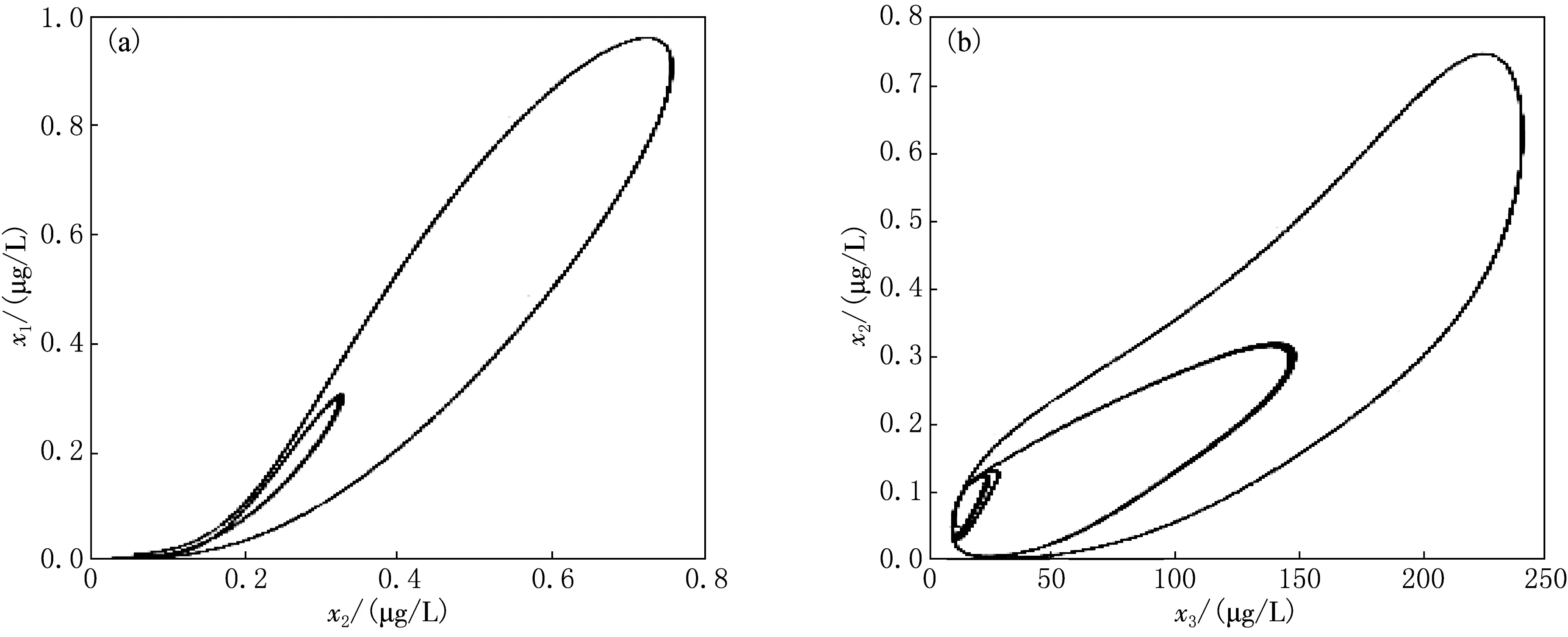
(a)GHRH-GH；(b)GH-IGFs

3.2 模型方程的混沌解

通過計算發現，初始迭代時，系統一般有個暫態過程，但當迭代次數很大時，隨時間的演化會導致一個確定的、對初值極為敏感的終態.終態可取無窮多個值，當a1在(7.5～9.2)×10-5之間變化時，方程組(6)的解是倍周期的，但當a1大于9.2×10-5時，系統就出現了多值狀態，是從周期分叉后進入混沌狀態的一種方式，是一條典型的通向混沌的道路.此時模型方程組為：

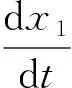
(7a)

(7b)

(7c)

求出其數值解的時域圖見圖6，由圖6可見，系統處于的是非周期振蕩狀態，各激素隨時間的分泌量不呈現規律的周期性，分泌峰值的大小不一致，每次到達峰值的時間間隔也不相同，但所有的峰值都限定在一個范圍中，不會無限變化，且與周期振蕩類似，在1 000 min內有5個峰值，呈現出典型的混沌行為.

為進一步展現混沌狀態的特征，做出系統方程組的相圖表達(見圖7).由圖7可見，系統經暫態后進入了多循環中，其運動軌跡被限定在相平面的有限區域內，呈現出密集的循環帶，這也是混沌的典型特征之一.

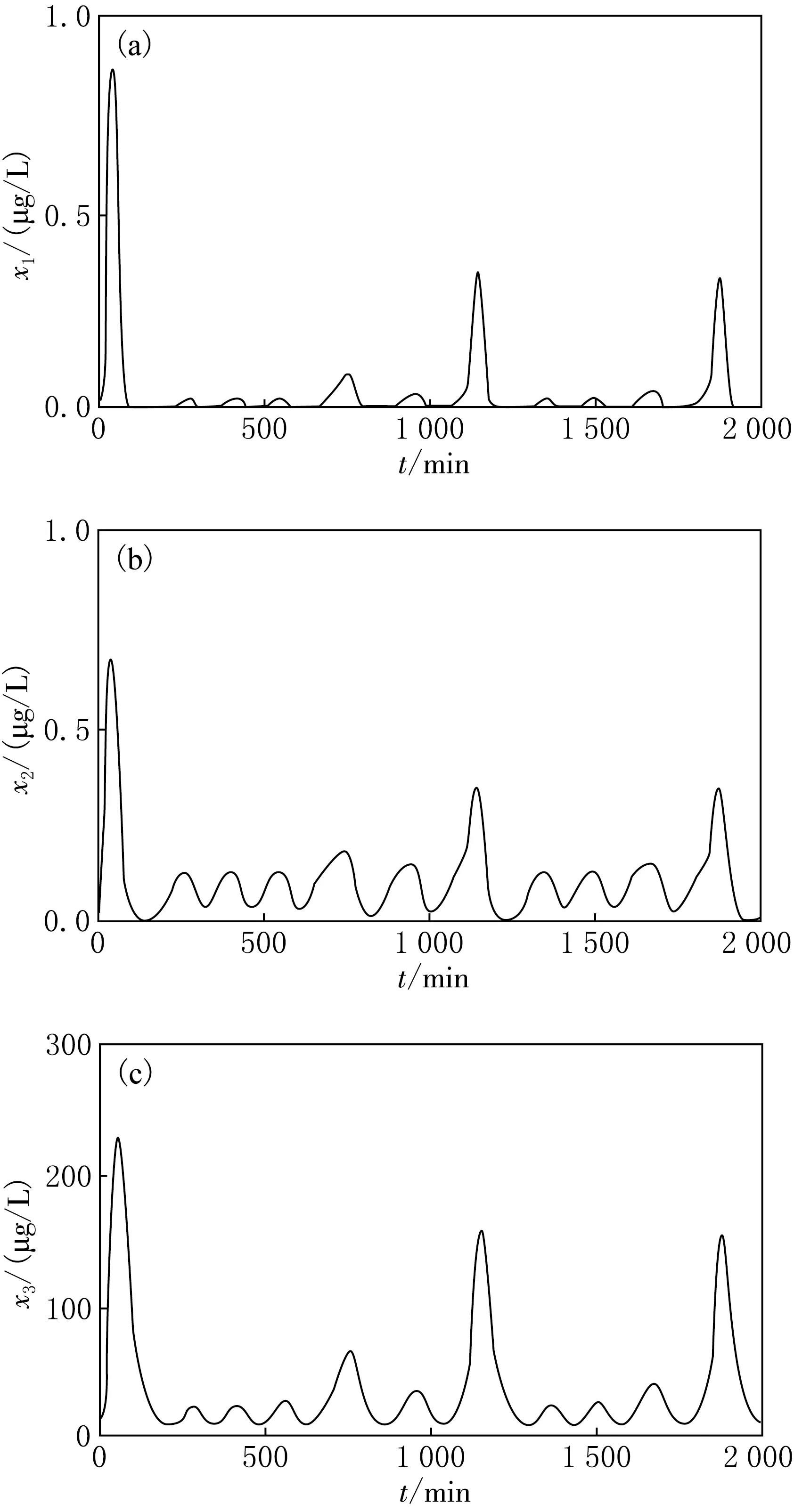
圖6 各激素混沌狀態的時域圖

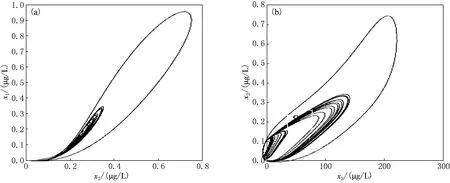
(a)GHRH-GH；(b)GH-IGFs

生長激素內分泌調節的模型及混沌行為研究表明，神經內分泌生長軸內激素分泌的正負反饋調節，使系統呈現出了典型的混沌狀態，而混沌態的存在，則表示生長激素內分泌調節一定服從非線性規律.