Banach 3-Lie代數(shù)上兩類映射的穩(wěn)定性
秦宇帆,林 潔,姜敬敬
(1.中國民航大學(xué)理學(xué)院,天津 300300;2.中國民航大學(xué)中歐航空工程師學(xué)院,天津 300300)
0 引言
1985年,F(xiàn)ilippov[1]引進(jìn)了n-Lie代數(shù)(或Filippov代數(shù))的概念.n元Lie積是n-線性、反對(duì)稱的,且滿足廣義的Jacobi恒等式.當(dāng)n=3時(shí),3元Lie積是Nambu括號(hào)的特殊情形,Nambu括號(hào)是由Nambu[2]在1973年引進(jìn)的,并且在物理上廣為人知.3-Lie代數(shù)被應(yīng)用于多重M2-膜的相關(guān)研究中,且其與數(shù)學(xué)、數(shù)學(xué)物理的許多重要領(lǐng)域有緊密聯(lián)系[3-4].因此,許多研究者對(duì)3-Lie代數(shù)感興趣.[5-12]
函數(shù)方程的穩(wěn)定性在1940年首次被Ulam[6]提出,他提出下列問題:在什么情況下存在一個(gè)可加映射逼近一個(gè)近似可加映射?設(shè)A和B是兩個(gè)Banach空間,Hyers證明了若ε>0,f:A→B滿足
‖f(x+y)-f(x)-f(y)‖≤ε,?x,y∈A,
則存在唯一的可加映射T:A→B使得
‖f(x)-T(x)‖≤ε,?x,y∈A.
近年來,不斷有這方面的成果涌現(xiàn)出來.文獻(xiàn)[7]給出了n階阿貝爾群G中函數(shù)方程
的廣義穩(wěn)定性結(jié)論和應(yīng)用(p是一固定的正整數(shù))[7];文獻(xiàn)[8]建立了關(guān)于函數(shù)方程
的3-Lie乘子的穩(wěn)定性和超穩(wěn)定性.
本文中,記C是復(fù)數(shù)域,N是自然數(shù)集.
1 預(yù)備知識(shí)
定義1.1[1]設(shè)A是一個(gè)向量空間,[-,-,-]:A×A×A→A是A上的一個(gè)3-線性反對(duì)稱運(yùn)算.若?x,y,a,b,c∈A有[x,y[a,b,c]]=[[x,y,a],b,c]+[a,[x,y,b],c]+[a,b,[x,y,c]],則稱(A,[-,-,-])為一個(gè)3-Lie代數(shù).
定義1.2設(shè)A是一個(gè)3-Lie代數(shù).若在A上存在一個(gè)范數(shù)‖·‖使得
‖[x,y,z]‖≤‖x‖‖y‖‖z‖,?x,y,z∈A,
則稱A為一個(gè)賦范3-Lie代數(shù).若(A,‖·‖)是一個(gè)Banach空間,則稱賦范3-Lie代數(shù)A為一個(gè)Banach 3-Lie代數(shù).
定義1.3[9]設(shè)A是一個(gè)3-Lie代數(shù),H,D,ɡ:A→A為線性映射.如果?x,y,z∈A,有H([x,y,z])=[H(x),H(y),H(z)],則稱H是A上的一個(gè)同態(tài);若?x,y,z∈A,有D([x,y,z])=[D(x),y,z]+[x,D(y),z]+[x,y,D(z)],則稱D是A上的一個(gè)導(dǎo)子;若存在線性映射ɡ1,ɡ2,ɡ3:A→A,使得
[ɡ(x),y,z]+[x,ɡ1(y),z]+[x,y,ɡ2(z)]=ɡ3([x,y,z]),?x,y,z∈A,
則稱ɡ是A上的一個(gè)廣義導(dǎo)子.
2 Banach 3-Lie代數(shù)上同態(tài)的穩(wěn)定性
引理2.1[10]設(shè)V和W是兩個(gè)C-向量空間.f:V→W是一個(gè)可加映射,滿足f(μx)=μf(x),?x∈V,μ∈T1∶={λ∈C||λ|=1},則f是C-線性的.
引理2.2設(shè)p是一個(gè)正整數(shù),f:A→A是一個(gè)映射,滿足
(1)
則f是C-線性的.
證明在(1)式中,取x=y=z=0,μ=1,則f(0)=0.再令(1)式中x=y=0,得pf(μz)=pμf(z),?z∈A,μ∈T1.故f(μz)=μf(z),?z∈A,μ∈T1.
下證f是可加的.用pz代替(1)式中的x,y,且令μ=-1,有
pf(z)=f(pz),?z∈A.
進(jìn)而有
pf(x+y)=f(px+py),?x,y∈A.
再用px,py分別代替(1)式中的x和y,且取z=0,得
pf(x+y)=f(px+py),?x,y∈A.
顯然有
f(px+py)=f(px)+f(py),?x,y∈A.
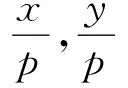
定理2.1設(shè)A是C上的一個(gè)Banach 3-Lie代數(shù),φ,ψ1:A×A×A→[0,+∞)是映射且滿足:
(2)
(3)
(4)
?x,y,z∈A.假設(shè)f:A→A是一個(gè)映射使得f(0)=0,且:
(5)
‖f([x,y,z])-[f(x),f(y),f(z)]‖≤ψ1(x,y,z),
(6)
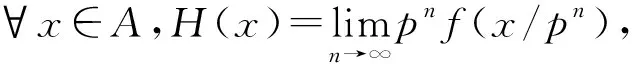
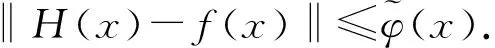
(7)
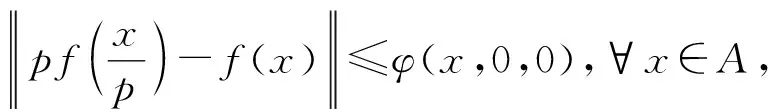

(8)
?x∈A,n∈N.用x/pm代替(8)式中的x,且不等式兩邊同乘pm得
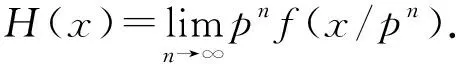
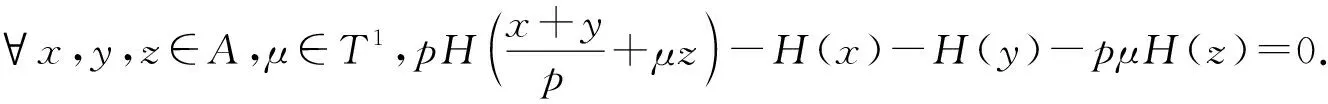
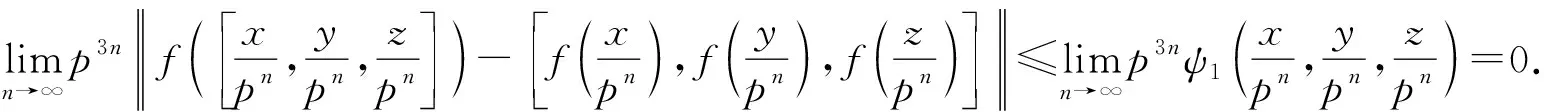
?x,y,z∈A.故H是一個(gè)同態(tài).
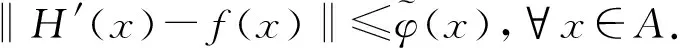
則
所以H′(x)=H(x),?x∈A.
推論2.1設(shè)A是一個(gè)Banach 3-Lie代數(shù),ε,p1,p2,p3,p4,p5,p6,p7,p8,q1,q2,q3是實(shí)數(shù)且滿足ε>0,p1,p2,p4,p6>1(或p1,p2,p4,p6<1),q1,q2,q3>1(或q1,q2,q3<1),f:A→A是一個(gè)映射使得f(0)=0且對(duì)?x,y,z∈A,
‖f([x,y,z])-[f(x),f(y),f(z)]‖≤
ε(‖x‖p1+‖x‖p2‖y‖p3+‖x‖p4‖z‖p5+‖x‖p6‖y‖p7‖z‖p8).
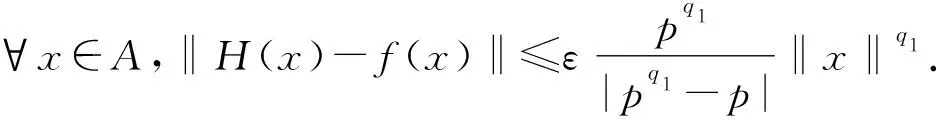
3 Banach 3-Lie代數(shù)上的導(dǎo)子的穩(wěn)定性
定理3.1設(shè)A是C上的Banach 3-Lie代數(shù),φ,ψ1:A×A×A→[0,+∞)是映射且滿足:
?x,y,z∈A.假設(shè)f:A→A是一個(gè)映射使得f(0)=0,且對(duì)?x,y,z∈A,μ∈T1,以下不等式成立:
‖f([x,y,z])-[f(x),y,z]-[x,f(y),z]-[x,y,f(z)]‖≤ψ1(x,y,z),
則存在唯一導(dǎo)子D:A→A使得
證明類似于定理2.1的證明,此處略去.
推論3.1在與推論2.1相同的條件下,f:A→A是一個(gè)映射,滿足f(0)=0,且
‖f([x,y,z])-[f(x),y,z]-[x,f(y),z]-[x,y,f(z)]‖≤
ε(‖x‖p1+‖x‖p2‖y‖p3+‖x‖p4‖z‖p5+‖x‖p6‖y‖p7‖z‖p8),
?x,y,z∈A.則存在唯一導(dǎo)子D:A→A滿足
4 Banach 3-Lie代數(shù)上的廣義導(dǎo)子的穩(wěn)定性
定理4.1設(shè)A是C上的一個(gè)Banach 3-Lie代數(shù),φ,ψ1:A×A×A→[0,+∞)是映射,滿足:
?x,y,z∈A.假設(shè)f,f1,f2,f3:A→A是映射使得f(0)=0,f1(0)=0,f2(0)=0,f3(0)=0,且:
‖[f(x),y,z]+[x,f1(y),z]+[x,y,f2(z)]-f3([x,y,z])‖≤ψ1(x,y,z),
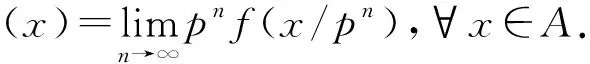
證明類似于定理2.1的證明,此處略去.
推論4.1在與推論2.1相同的條件下,f,f1,f2,f3:A→A是映射,f(0)=0,f1(0)=0,f2(0)=0,f3(0)=0,且滿足:
‖[f(x),y,z]+[x,f1(y),z]+[x,y,f2(z)]-f3([x,y,z])‖≤
ε(‖x‖p1+‖x‖p2‖y‖p3+‖x‖p4‖z‖p5+‖x‖p6‖y‖p7‖z‖p8),