普通高中數學課堂“起點”影響“效點”

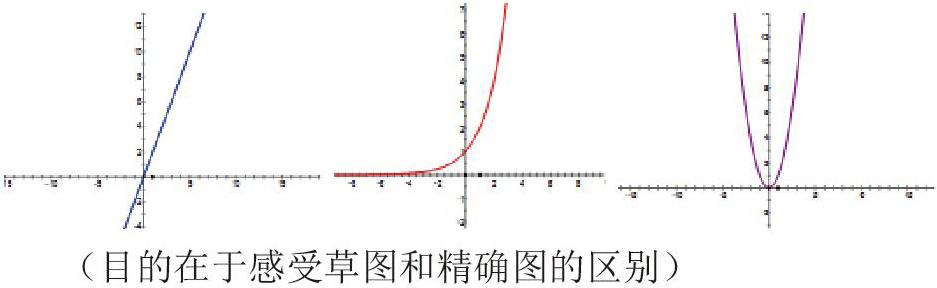
普通高中數學課的教學起點不易過高，不易過難，應當充分了解學生的最近發展期，全面分析學生的近況學情，找到本節數學課的生長點，一步一步的引領學生去探究數學問題、思考數學問題。教師應服務好學生，給學生創造可獲得成功的機會，學生也才能不斷獲得成就感，如果說學生自己經過不斷思考，不斷動筆試算試探實現了不同的“小成功”，學生才能在數學課的探索學習過程中找到“樂趣”。相反，如果數學課起點過高，過難，與學生的最近發展期關系不大甚至背離，易給學生增大挫敗感的可能，從而導致學生對學數學失去信心，“怕”數學。

下面是我最近上的一節數學示范課，拿出來和大家一起分享一下：這節課是人民教育出版社出版的2020年普通高中教科書A版，數學必修第一冊第四章《4.4.3不同函數增長的差異（第一課時）》。

我是這樣教學的：

學生在初中已經學過了一次函數，且對一次函數已經擁有了較為牢固的基礎知識，在高一新教材第三章3.3冪函數，第四章4.2指數函數分別學過了冪函數和指數函數，學生對冪函數和指數函數的圖像和性質已經掌握了扎實的基礎知識和基本技能的條件下，《4.4.3不同函數增長的差異（第一課時）》就水到渠成的可以發展了。

我的設想如下：

1.在不同坐標系中分別畫出以下函數的草圖，為了后面教學的需要做好了準備工作（后面要在同一坐標系中畫圖作比較）;

2.畫草圖學生應該都會畫（設計目的在于能讓全部學生都參與進來）;

3.不同的學生所畫出的草圖是有差異性的（后面讓學生體會誤差，錯誤帶來的麻煩）;

下面是精確的畫圖。（復習回顧精確畫圖的過程：列表、描點、連線。為學生后面精確畫圖作準備）

問題驅動：

驅動1.同學們能觀察出三個草圖有什么共同的特征嗎？（目的是把學生引入在第一象限都是單調遞增函數）

驅動2.雖說三個函數在第一象限都是單調遞增函數，但增長變化的情況有什么不同？（目的是讓學生自己從草圖中發現三個函數在第一象限增長的快慢不一樣）

學生畫的草圖情況較為豐富，有部分同學的一次函數和指數函數沒有交點，有部分同學的一次函數和指數函數有一個交點感覺像“相切”，有部分同學的一次函數和指數函數相交但只有一個交點，有部分同學的一次函數和指數函數相交有兩個交點，

此時，多給學生思考的時間。

結果是不一樣的，同學們討論導致結果不一樣的原因是什么？

經過學生討論，最后同學們能自己得出不同的草圖導致結果的不同，那如何才能得出正確的結果呢？

學生們都知道要精確畫圖，才能探究出正確的結果（用前面精確畫圖的過程畫圖）

（當遠遠小于的情況，下一節課我們再探究，同學們課后自己可以先思考。）

這節數學課，同行們觀察到全班學生從頭到尾都參與在數學探索的學習過程中，都沉浸在思考和動筆試算試探的氛圍中，感覺整節數學課課堂數學味道很濃，課堂氣氛也很自然，很和諧，究其原因是起點低且恰當，適合學生，學生們在整節課中經過認真的思考，整節課一直不斷的獲得成功，層層遞進，讓學生潛移默化的知道不同的函數增長是有差異性的。總之，普通高中的數學課堂應該在充分了解學生學情的情況下，設置低起點的教學“門檻”，學生才能更好的“進門”，巧用恰當的問題串，不斷引領驅動學生自主探究學習，讓學生不斷獲得成就感，從而不斷激發學生思考數學探究數學的動力，以使學生對數學產生濃烈的學習興趣，數學學習效率才會更有效，這樣普通高中學生的數學未來才可期，加油。

昆明市西山區實驗中學 趙永祥