用于雙有源橋DC-DC 變換器的全局效率最優調制方法

韓會山，畢艷軍，梁 舒

(邢臺職業技術學院電氣工程系，河北 邢臺054000)

隨著社會進步，新能源的發展逐步成為各個國家的首要戰略目標。 雙有源全橋(Double Active Bridge，DAB)雙向DC-DC 變換器以其控制方式靈活、動態響應快、結構對稱等特點，以及易于串并聯，適應高低壓變化，具備能量雙向傳輸等優點，得到了廣泛的關注[1-2]。 同時，DAB 變換器在電動汽車與電網互動(V2G)、儲能系統和電源供電系統等方面具有重要的應用前景[3-4]。

自從DAB 變換器被提出以來，相關研究主要集中在其調制策略、功率傳輸特性、軟開關實現以及控制方法等方面。 在調制策略方面，通常包含有單移相調制(SPS)、雙重移相調制(DPS)和三重移相調制(TPS)等。 SPS 調制方式是最常用的調制方法之一，其控制方法簡單，但無法調節和控制變換器回流功率與電感電流有效值[5]。 一些學者認為DAB 變換器存在功率回流現象造成了傳輸效率的下降，從減少回流功率方面研究了DPS 等調制方式。 其中，文章[6]所提方法降低了DAB 變換器運行時的無功回流功率。但對于DPS 調制方式來說，電路系統的無功環流仍舊很高，這限制了變換器系統進一步提高傳輸效率。TPS 調制方式涵蓋了SPS 與DPS 調制方式，理論上可以實現更優的控制效果[7]。 文章[8]提出一種TPS調制策略，提高了DAB 變換器的傳輸效率，計算出了最優控制量使DAB 變換器擁有最小化的電流應力和導通損耗。 該方法雖然減小了電感電流，但并沒有直接以效率最優為控制目標，因此其傳輸效率未在最優狀態。 此種方式下，建立精確而復雜的最優效率目標函數將導致全局最優調制參數難以被確定。

本文提出了一種基于粒子群優化(PSO)算法的DAB 變換器全局效率最優調制方法。 其根據變換器系統的電路參數與實時的工作狀態建立了精確的最優效率目標函數。 設計三重移相占空比控制器，可以根據給定的傳輸功率，利用PSO 算法搜索系統最優調制參數，從而得到最優三重移相占空比，使得DAB 變換器在全負載范圍內始終工作在傳輸效率最優的狀態。

1 電路拓撲與數學模型

圖1 為DAB 變換器的電路拓撲結構，其由開關管Q1～Q8構成的兩個電壓源型有源全橋、高頻變壓器T1、諧振電感Lr、以及兩個直流母線支撐電容C1、C2組成。 在該拓撲中，Lm為高頻變壓器的勵磁電感。在移相調制策略中，各個橋臂的上下開關管均為互補驅動信號。 一、二橋臂的橋口輸出電壓為vp；三、四橋臂的橋口輸出電壓為vs；一次側直流母線電壓值為V1；二次側直流母線電壓值為V2；電感Lr兩端電壓為vL；電流為iL。 定義變換器的開關周期為2T。

在TPS 調制方式下，DAB 變換器各個開關管的驅動信號波形和橋口電壓波形vp、vs如圖2 所示。

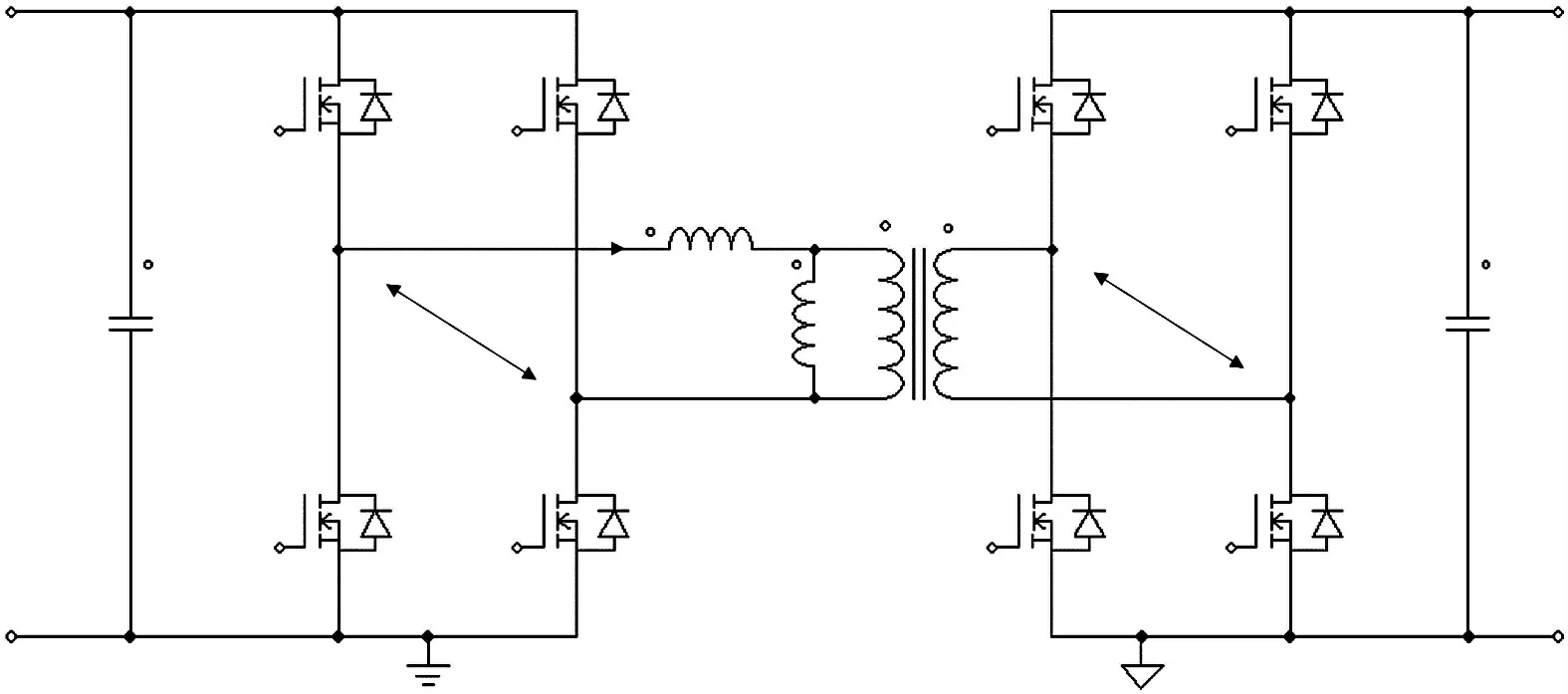
圖1 DAB 變換器電路拓撲

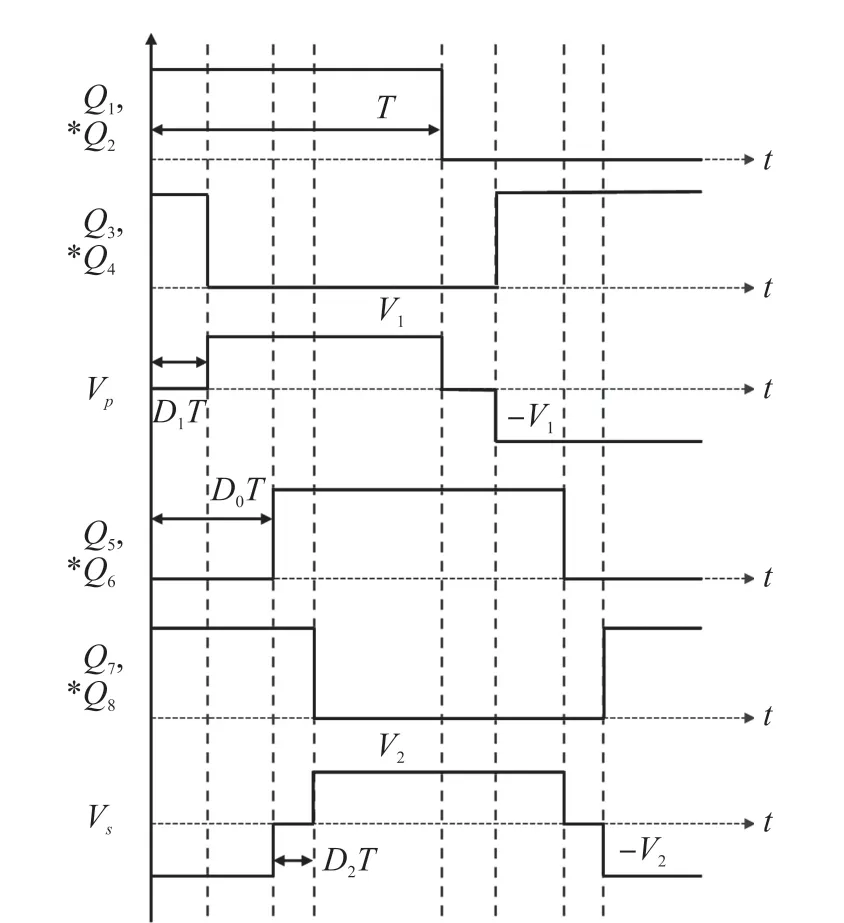
圖2 DAB 驅動波形與橋口電壓波形

TPS 調制方式下，所有開關管都為50%占空比。其中開關管Q1、Q2的驅動信號分別超前開關管Q5、Q6為D0×180°；開關管Q1、Q2的驅動信號分別超前開關管Q4、Q3為D1×180°；開關管Q5、Q6的驅動信號分別超前開關管Q8、Q7為D2×180°。 其中，移相占空比D0取值范圍為-1 ～1，D1取值范圍為0 ～1，D2取值范圍為0～1。 可以看出，TPS 調制方式擁有三個控制自由度，可以通過適當選取三個控制變量，使DAB 變換器工作在效率最優狀態。

如式(1)定義方波函數S(t)，占空比為0.5、周期為2T。

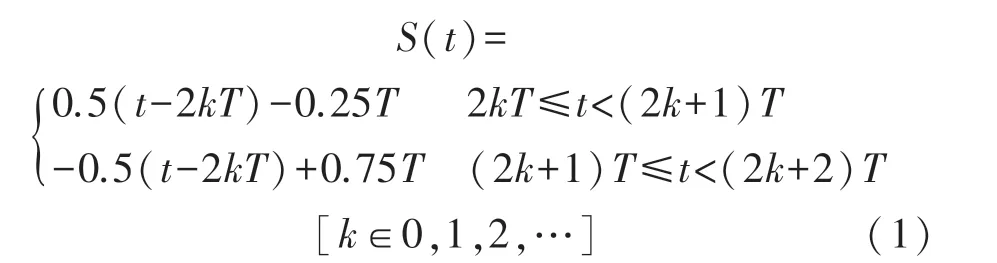
根據圖2 可知，橋口電壓波形vp(t)、vs(t)為如式(2)、式(3)所示的三電平方波。

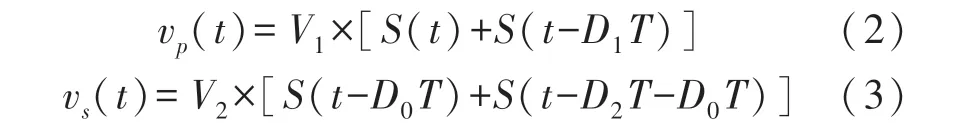
根據電路拓撲結構與vp(t)、vs(t)公式，可以簡化DAB 變換器的數學模型如圖3 所示。 其中，原副邊全橋分別被簡化為兩個串聯的電壓源，高頻變壓器在理想情況下被省略，n 為變壓器的變比。

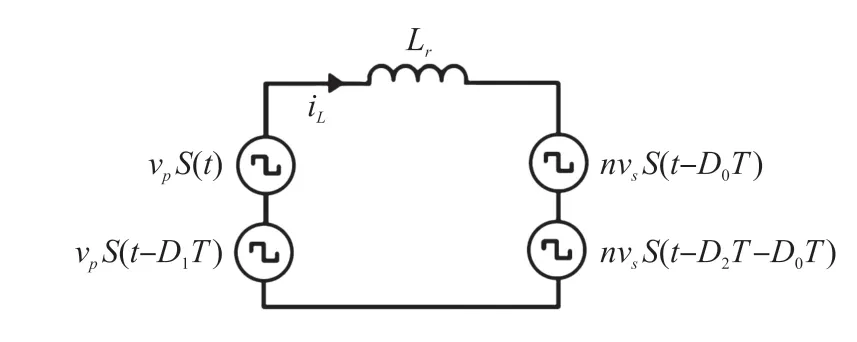
圖3 DAB 變換器等效模型

根據圖3 及電感伏秒平衡公式，可以推導出變換器穩態工作時電感電流的有效值平方表達式與變換器的傳輸功率表達式，分別如式(4)、式(5)所示。

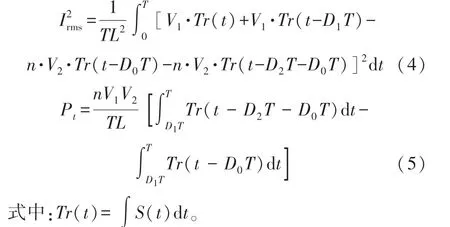
對于不同的D0、D1、D2，式(4)、式(5)的形式不同，因此傳統方法無法對不同工作點進行統一的分析。 設置直流電壓V1為500 V，V2為240 V，開關頻率為20 kHz，變壓器變比為1 ∶1，Lr為47 μH。 根據式(4)、式(5)與TPS 占空比的取值范圍，可以建立三維傳輸功率分布圖與電感電流有效值平方分布圖，分別如圖4、圖5 所示。

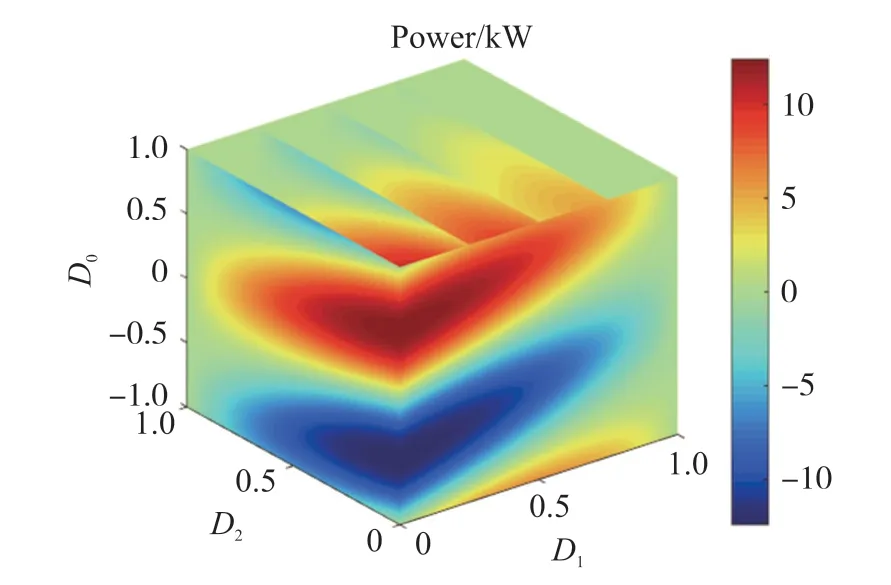
圖4 DAB 變換器傳輸功率分布圖

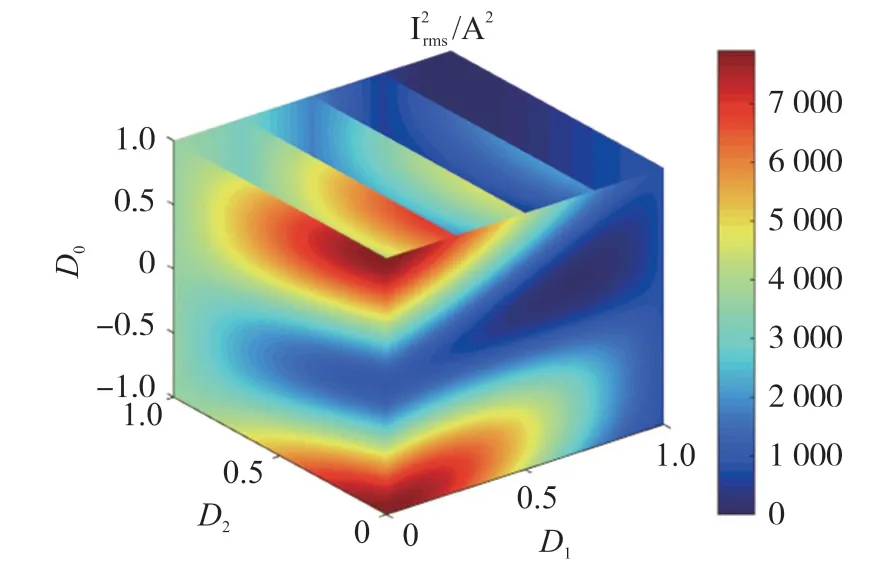
圖5 DAB 變換器電感電流均方值分布圖

圖4 與圖5 中，三維坐標系中任意一點的坐標分別對應三重移相占空比D0、D1、D2。 該點的顏色深淺表示相應取值的大小。 對應于某一給定的傳輸功率，輸入變量有多種不同的組合形式。 對于這些不同組合形式，得到的電感電流有效值不同。 在DAB 變換器中，由于電路存在阻抗，電感電流造成了變換器的功率損失。 通過相關算法對輸入變量D1、D2、D3進行合理規劃，將會得到一種最優組合，使變換器傳輸功率一定時，對應的功率損失最小，這樣變換器就能工作在效率最優的狀態下。

2 改進粒子群優化算法

PSO 算法屬于AI 智能算法，具有實現較為簡單、控制參數少且不依賴目標函數的特點。 目前，部分學者在電力電子技術相關的問題中嘗試應用PSO理論，并取得了很多研究成果[9]。

三維空間中粒子群算法模型如式(6)、式(7)所示。

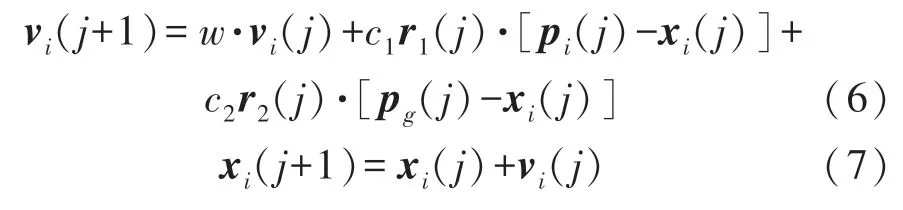
向量xi(j)表示粒子在三維向量空間中的位置，下標“i”表示第i 個粒子，“j”表示粒子的第j 代；vi(j)為粒子的速度向量，表示粒子運動快慢；向量pg(j)、pi(j)分別為粒子群群體的最優位置與個體的最優位置；ck為粒子的加速度常數；w 為慣性權重系數；rk(j)為三維均勻分布隨機函數，其每個維度的取值范圍為0～1；N 為粒子總數；J 為最大迭代次數。

PSO 算法通常更適用于求解非約束優化問題，在求解非線性約束問題時，需要如式(8)構造帶有懲罰因子的廣義目標函數改進粒子群算法。 其中，每一個粒子的適應度函數為F(xi(j))＝F(D0，D1，D2)，以最小值為目標。

式中:f(xi(j))為原目標函數，如式(9)所示；h 為懲罰力度(通常取500～1 000)；H(xi(j))為懲罰因子，如式(10)所示；Ω 為xi(j)的可行域，由D0、D1、D2的取值范圍確定。

式(9)中目標函數f(xi(j))設計為系統總損耗，當系統損耗最低時，認為傳輸效率最高。 其中系統損耗包括了線路內阻損耗與開關損耗。 當使用IGBT 開關管時，還應包含IGBT 壓降產生的導通損耗。

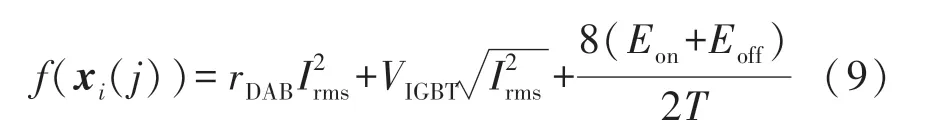
式中:rDAB為回路總內阻，VIGBT為回路中IGBT 的總壓降，(Eon+Eoff)為單個開關管的開關損耗能量，通常可以從器件的數據手冊中得出。

式(10)的懲罰函數保證了輸出功率等于給定傳輸功率。

根據粒子群算法模型，DAB 變換器全局效率最優控制方法如下，共分為9 個階段。

階段1，初始化粒子群:初始時刻，根據經驗設置加速度常數c1、c2(通常為0 ～2)、慣性權重w(通常為0.5～1)、粒子數量N(通常為200 ～500)、最大迭代次數J(通常為500 ～2 000)。 隨機設置粒子群內各個粒子的起始位置xi(0)，并根據式(8)對每一個粒子的適應度進行求解。 依此設置粒子群群體最優位置pg(0)與個體最優位置pi(0)。 初始化粒子的初速度vi(0)(粒子每個維度的初始速度通常為0～0.2)。 執行階段2。

階段2，變量更新:更新電壓值V1、V2；傳輸功率給定Pset；電感值Lr。 執行階段3。

階段3，粒子位置計算:根據式(7)計算并更新粒子群內每一個粒子的最新位置。 若計算位置超出可行域，則通過降低當前速度vi(j)，將粒子限制在系統所劃定的可行域邊界之內。 執行階段4。

階段4，加入微小擾動:若發現某粒子的速度為零，則如式(11)所示，加入微小擾動(z 通常小于0.05)。 此方法避免了粒子群內的粒子靜止不動，有利于提高PSO 的動態性能。 執行階段5。

vi(j+1)＝vi(j+1)+z·r(j) (11)

階段5，粒子速度計算:根據式(6)計算并更新粒子群內每一個粒子的速度。 執行階段6。

階段6，粒子適應度計算:根據式(8)～式(10)，計算并記錄粒子群各個粒子的適應度函數F(vi(j+1))，用于之后的位置更新。 執行階段7。

階段7，個體最優位置更新:根據階段6 中的記錄結果與歷史個體最優位置的適應度函數比較。 若某粒子當前位置的適應度較優，則更改該粒子的個體最優位置pi(j+1)為當前所處位置。 執行階段8；

階段8，群體最優位置更新:根據階段6 中的記錄結果找到本輪迭代內的群體最優位置，并與群體最優位置比較適應度，將較優位置設置為群體最優位置pg(j+1)。 執行階段9；

階段9，終止條件判斷:將群體最優位置的坐標作為TPS 占空比D0、D1、D2輸出給開關管驅動單元。 判斷當前迭代次數，若達到最大迭代次數，則此次粒子群優化結束，否則跳回階段2 繼續執行PSO算法。

利用上述方法可以處理復雜的全局效率最優目標函數，同時可以實時尋優三重移相占空比，使DAB 變換器在全負載范圍內以最優傳輸效率運行。保持了較低的回流功率、電感電流峰值和有效值。

3 仿真與實驗驗證

為了驗證本文所提方法的有效性與正確性，首先在MATLAB 環境下對其進行了仿真驗證，其次搭建平臺進行了實驗驗證。 設置直流電壓V1為500 V，V2為240 V，開關頻率為20 kHz，變壓器變比為1 ∶1，Lr為47 μH。

圖6 為DAB 變換器在不同給定功率時的MATLAB 閉環仿真波形。 仿真波形分別為Vp(t)、Vs(t)電壓波形與電感電流波形，分別標記為VB1、VB2與IL。

圖6 分別顯示了不同傳輸功率時的工作波形，變換器正常工作。 進一步，隨著給定功率增加，PSO優化后的TPS 占空比的變化軌跡如圖7 所示。

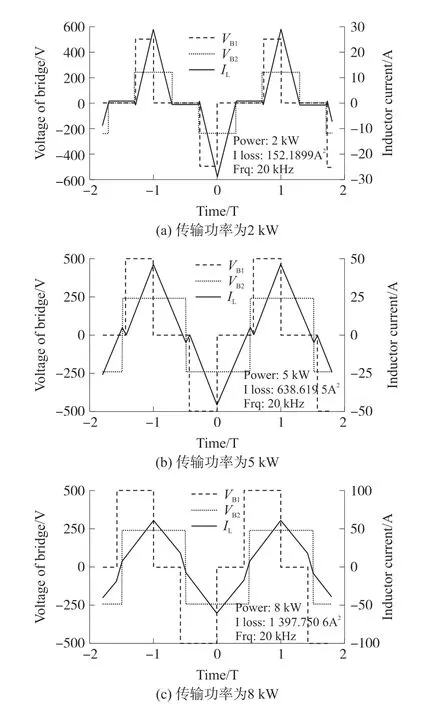
圖6 不同給定功率下的閉環仿真波形

圖7 PSO 優化后的TPS 占空比軌跡

可以看出，變換器的最優調制方式從TPS 調制方式，DPS 調制方式到SPS 調制方式逐漸變化。 在全工作范圍內，本文所提方法均能對三重移相占空比進行尋優，并能實時得到最優控制量，使DAB 變換器在全負載范圍內以最優傳輸效率運行。

如圖8 所示為傳輸功率為8 kW 時的實際電路工作波形，圖中分別表示了Vp電壓波形、Vs電壓波形與電感電流波形iL。 此時原邊電壓峰值為500 V，副邊電壓峰值為250 V，電感電流有效值約為36 A，實驗結果與仿真結果一致，證明了本文所提調制策略下DAB 變換器可以正常穩定的工作。

圖9 所示波形分別為同一DAB 變換器下的SPS方式效率曲線、DPS 方式效率曲線、TPS 方式效率曲線與經過本文PSO 算法優化后的TPS 效率曲線。

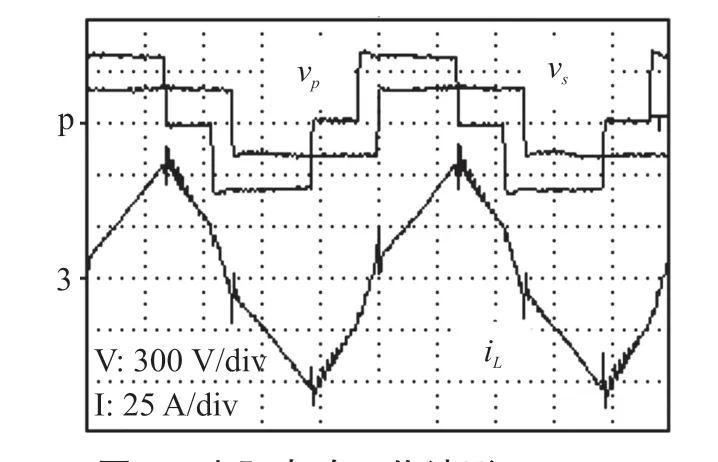
圖8 實際電路工作波形(8 kW)

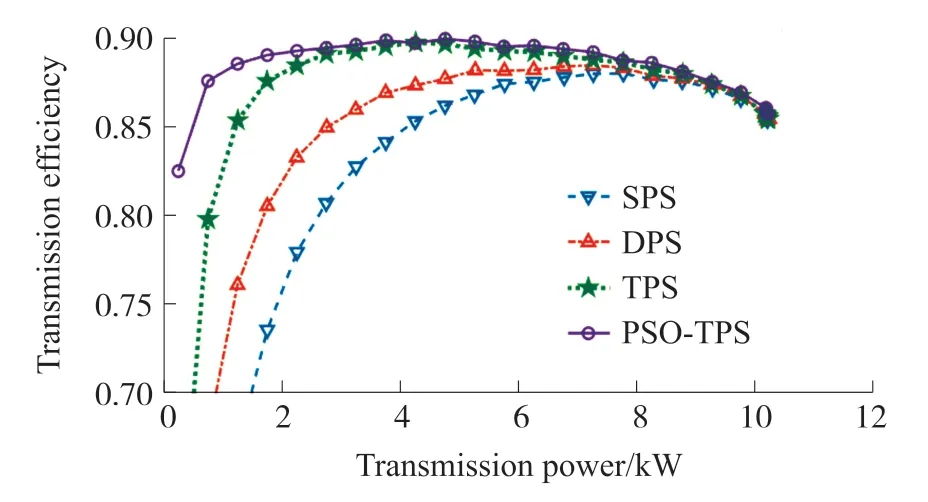
圖9 DAB 變換器效率對比曲線

由圖9 得出，全工作范圍內，本文算法下的TPS方式傳輸效率優于傳統的SPS、DPS 方式與經典TPS 方式。 相比于經典TPS 方式，本文所提方法顯著提高了變換器在輕載時的效率。 實驗結果驗證了粒子群算法應用在實現DAB 變換器全局效率最優的三重移相占空比尋優方法上的正確性與可行性，也說明了所提方法的實際應用價值。

4 結論

針對TPS 調制方式下，難以建立精確而復雜的最優效率目標函數的問題，提出了一種基于粒子群優化(PSO)算法的DAB 變換器全局效率最優調制方法。 該方法根據變換器參數、工作狀態和給定傳輸功率實時搜索系統最優調制參數，得到最優三重移相占空比，使得DAB 變換器在全負載范圍內始終工作在傳輸效率最優的狀態，且保持較低的回流功率、電感電流峰值和有效值。 本文通過MATLAB 仿真與實驗驗證了該算法的性能，證明了所提方法的正確性與實際的可行性。