一個具有無限多吸引子共存的新混沌系統的動力學分析及其電路實現*
孫 亮,羅 佳*,喬印虎
(1.池州職業技術學院機電技術系,安徽 池州247000;2.安徽科技學院機械工程學院,安徽 鳳陽233100)
自從1963 年發現Lorenz 混沌吸引子以來[1],各種新混沌系統不斷被發現和研究,如1999 年陳關榮教授等人[2]提出的Chen 系統,2002 年呂金虎教授等人[3]提出的Lü 系統、2004 年劉崇新教授等人[4]提出的Liu 系統以及其他的擴展混沌系統[5-6]。 近年來,研究發現,許多的混沌系統具有共存吸引子特性,即多穩定性[7-9]。 具有多穩定性的混沌系統比一般混沌系統具有更大的不確定性,在信息加密和保密通信等領域具有極高的應用價值[10-11]。 特別是2016 年包伯成教授等人[12]在一個憶阻電路中發現了超級多穩定性現象,即在確定的混沌系統中存在無限多個吸引子共存特性。 此后,超級多穩定性現象在各種混沌系統中被陸續發現和研究[13-16]。 本文提出了一個新的三維連續混沌系統,該系統僅含有2 個非線性項,不僅具有一般混沌系統的特性,重要的是其能夠表現出豐富的超多穩定性,即在確定的參數情況下,不同的初始值能夠得到無限多種不同的混沌吸引子。 同時為了在實際工程中更好地應用此系統,設計了系統的實現電路并進行了仿真實驗,實驗結果驗證了數值仿真的正確性。
1 新的三維混沌系統
新系統動力學方程為:
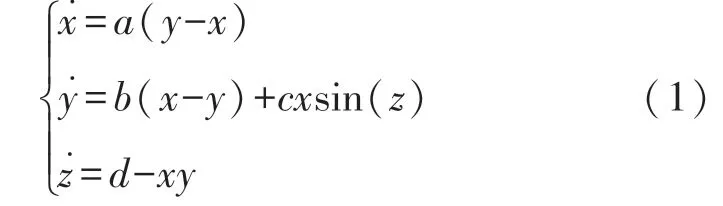
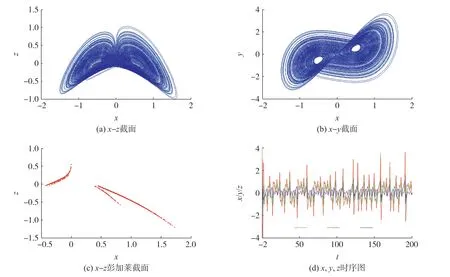
圖1 混沌吸引子相圖
式中:x,y,z 為3 個系統狀態變量,a,b,c,d 為4個正的系統參數,xsin(z)和xy 為2 個非線性項。當參 數a =1,b =0.5,c =12,d =0.3,初 值 為(2,2,2)時,系統具有雙翼混沌吸引子,如圖1(a)、(b)所示,圖1(c)為y =0 時的x-z 彭加萊截面,可以看出彭加萊截面為不規則的分段曲線,說明此時系統處于混沌狀態。 圖1(d)為系統3 個變量隨時間變化的時序圖,可以看出產生的序列具有無周期性,進一步證明此時系統處于混沌狀態。
2 新系統的動力學分析
2.1 耗散性
通過對系統(1)中3 個非線性方程等式分別求偏導,可以得到系統的散度為:
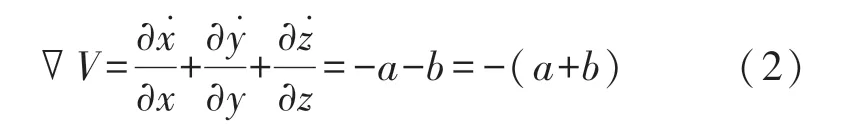
顯然,當a>0 且b>0 時,?V 恒小于0,系統(1)是耗散的。 在此條件下,系統以指數形式收斂dv/dt=e-(a+b),這意味著,當t 趨于無窮大時,系統軌線上每一個小體積元收斂到0,系統的軌跡逐漸趨于一個有界的吸引子。
2.2 平衡點穩定性
令系統(1)等式右邊等于0,可以得到系統的平衡點狀態方程如下:
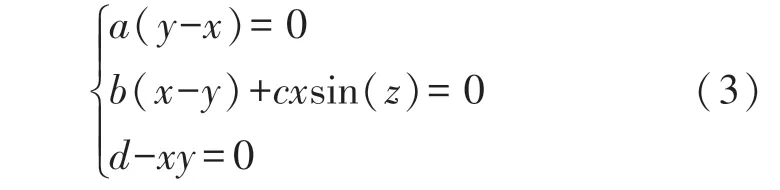
解平衡方程(3)可以得到無限多個系統平衡點,如下所示:
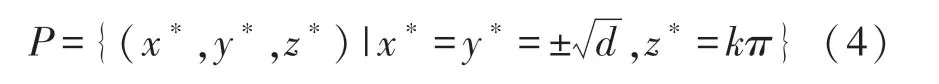
式中:k =0,±1,±2,±3,±4,…。 計算系統Jacobi 矩陣為:
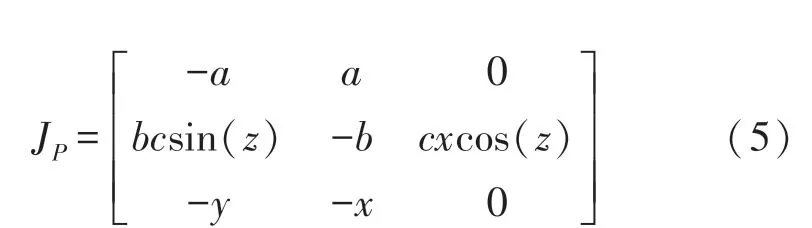
所有平衡點P 均有以下特征方程:

顯然,對于所有正參數,基于勞斯穩定性判定定理,系統(1)的所有平衡點均具有不穩定性特性。
2.3 參數對系統特性的影響
當保持系統參數a =1,b =0.5,c =12 不變,初值分別設為(2,2,2)和(2,2,-2),系統隨參數d 變化的分岔圖如圖2 所示,其中縱坐標為x 變量最大值。在圖2 中,紫色表示初值(2,2,2)條件下系統產生的分岔結果,藍色表示初值(2,2,-2)條件下系統產生的分岔結果。 從圖2 可以發現,隨著參數d 從0開始正向增大,系統動力學軌跡通過正向倍周期分岔路徑從周期行為快速進入到混沌狀態,直到d =0.64。 需要指出的是,在此混沌區間內系統存在少數窄周期窗特性。 隨后系統又開始從混沌行為反向倍周期分岔進入周期行為,并在d =0.76 時通過切分岔路徑快速演變為混沌行為。 隨著d 的進一步增大,系統再次通過反向倍周期分岔途徑在d =1.1 時進入到周期狀態,隨后系統保持周期狀態穩定不變。此外,從圖2 中還可以明顯的觀察到兩個特點:一是系統的混沌吸引子幅度與d 密切相關;二是在部分d 的取值范圍內存在共存吸引子現象。 為了進一步證實系統(1)的參數變化特性,圖3 給出了初值(2,2,2)條件下,系統隨參數d 變化的Lyapunov 指數譜,當d 在(0.1,0.64)與(0.74,1.1)范圍內,系統Lyapunov 指數分布為(+,0,-),根據李雅普諾夫指數判定定理,說明系統是混沌的。 從圖3 可以看出,系統在d ∈(0,0.1),d ∈(0.65,0.73),d ∈(1.2,1.5),區間內以及d =0.4,d =0.46,d =0.592 時,Lyapunov 指數分布為(0,-,-),說明系統是周期的。Lyapunov 指數譜所表現的系統動力學狀態分布與分岔圖基本一致。
在MATLAB 中設置時間步長為0.01,最大時長為2 000,新系統對于參數d 取不同值所得到的混沌吸引子相圖如圖4 所示。 由圖可看出:當d =0.2 時,系統產生了一個雙翼混沌吸引子;當d =0.8 時,系統產生了一個4 翼混沌吸引子;當d=0.85 時,系統產生了一個6 翼混沌吸引子;當d=1.02 時,系統產生了一個共存的雙翼混沌吸引子。 該新系統在不同參數值下產生了不同的混沌吸引子,特別是在z 方向上分離產生了多翼吸引子,具有復雜的動力學行為。

圖2 參數d 分岔圖

圖3 參數d Lyapunov 指數譜
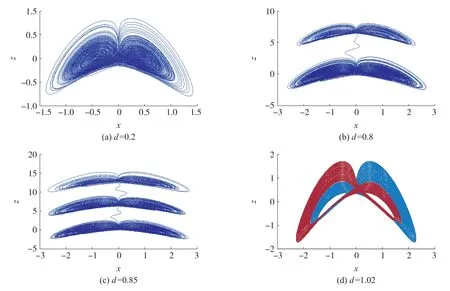
圖4 新系統在不同d 值時混沌吸引子相圖
2.4 初值對系統特性的影響
盡管混沌系統對變量的初始值具有高度敏感性,但大部分的系統在不同的初值下,運行軌跡最后都收斂到有限個吸引子上,而對于不同初始值導致系統運行軌跡收斂到無限個不同的吸引子上的現象被稱為共存無限個吸引子現象,或稱超多穩定性行為。
分析發現,當固定參數a =1,b =0.5,c =12 和d =0.3,初值x(0)=2,y(0)=2 保持不變,在不同的初值z(0)條件下,新系統(1)能夠產生無限多種混沌吸引子共存現象,即新系統具有超多穩定性。 如圖5 所示,當z(0)分別設置為-2π,0,2π,4π,6π,8π 時,對應的混沌吸引子分別為紫色,紅色,綠色,黃色,淺藍色和深藍色吸引子。
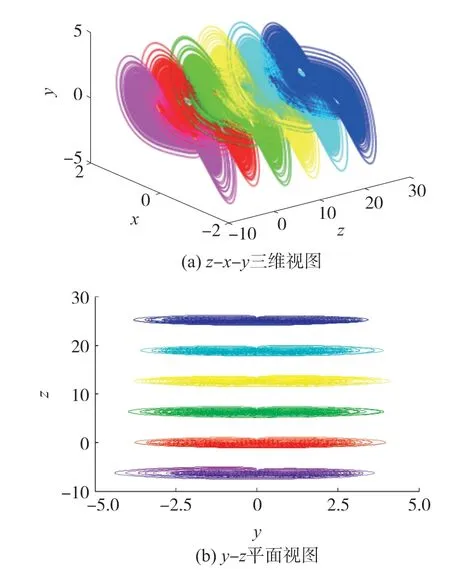
圖5 初值z(0)影響下的共存混沌吸引子
保持系統參數不變,圖6 給出了系統(1)隨初值z(0)變化的分岔圖。 由圖6 可知,對于更多不同的z(0)值,系統(1)能夠產生更多的共存混沌吸引子。 它進一步說明了新系統中無限多個混沌吸引子共存現象的客觀存在性。 此外,如果設置參數a =1,b =0.5,c =12,d =1.2,同樣取不同的初值z(0)為-2π,0,2π,4π,6π,8π,系統(1)能夠產生無限多個共存周期吸引子,如圖7 所示。
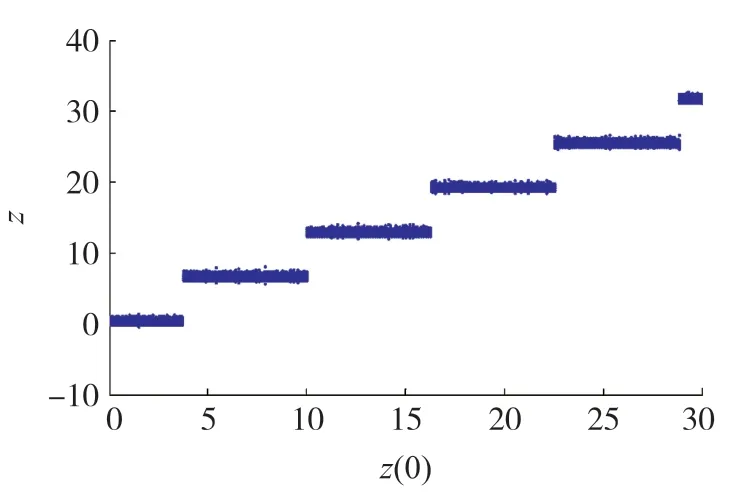
圖6 系統隨z(0)變化的分岔圖
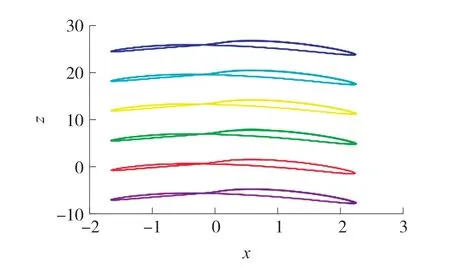
圖7 初值z(0)影響下的共存周期吸引子
3 電路設計與仿真
混沌系統的電路實現對于實際工程應用具有根本的重要性[17-18]。 利用模擬運算放大器,模擬乘法器,正弦信號轉變器以及電阻、電容對系統(1)進行電路設計與實現。 圖8 給出了系統的電路圖。 系統狀態變量x,y,z 通過3 個積分器的輸出電壓表示。基于基爾荷夫電路定律,系統電路的等效電路方程為:
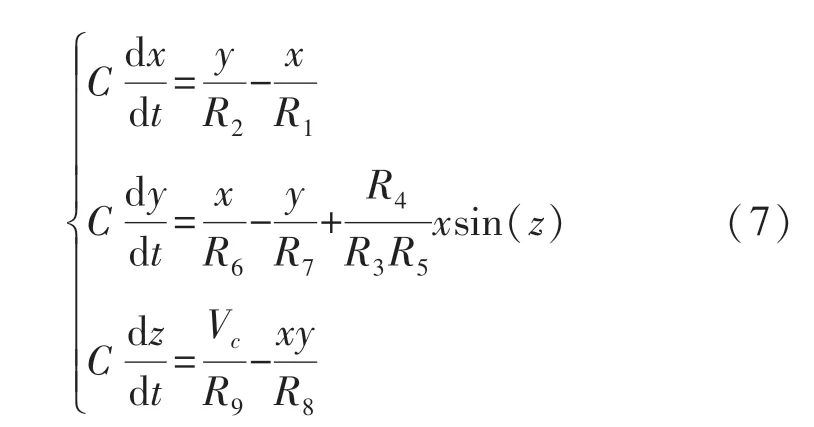
比較系統參數與電路元件,參數a =R/R1=R/R2,b =R/R6=R/R7,c=R4/R3,d =Vc/R9。 在Multisim電路仿真軟件中創建圖8 所示電路,當a =1,b =0.5,c=12 時,對應電路元件值設置為C =10 nF,R =10 kΩ,R1=R2=100 kΩ,R6=R7=200 kΩ,R5=R9=100 kΩ,R4=10 kΩ,R3=0.9 kΩ。 當d =0.3 和d =1.2 時,調節Vc值分別為0.33 V 和1.3 V,仿真結果分別如圖9(a)和圖9(b)所示。
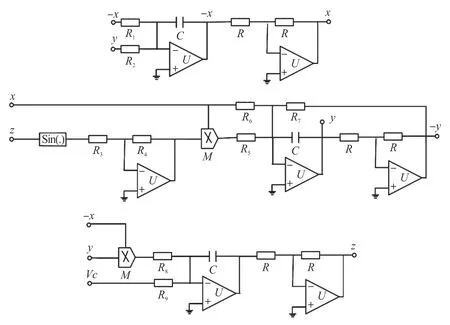
圖8 系統電路原理圖
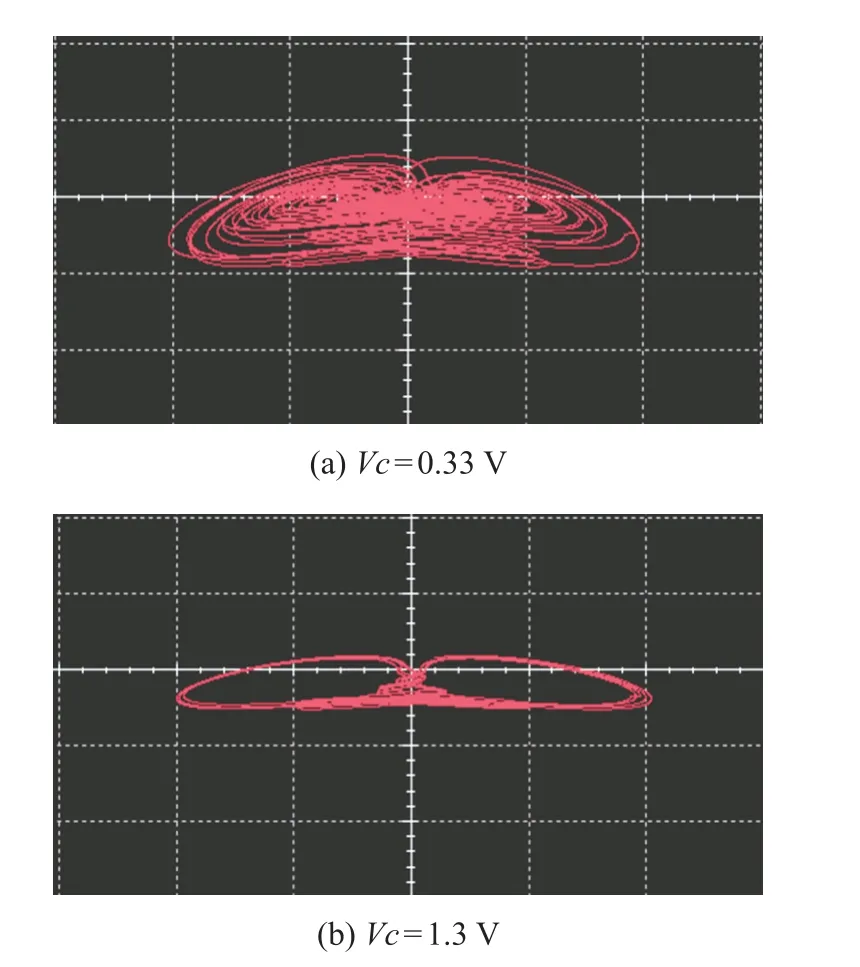
圖9 Multisim 仿真結果
4 結論
本文針對一種具有無限多吸引子共存的三維連續混沌新系統,進行理論分析,MATLAB 數值計算和電路設計仿真研究。 研究結果表明,該系統在不同的系統參數下能夠產生不同的多翼混沌吸引子,具有豐富的動力學特性。 特別是在固定系統參數下,通過改變初始值,該系統能夠產生無限多吸引子共存的超多穩定性動力學行為。 通過設計模擬電路,用Multisim 得到新系統的一種混沌吸引子和一種周期吸引子,從而證實了系統的可實現性。 如此超多穩定性混沌系統,在保密通信中具有較高的應用價值。

