挖掘習題講評的深度 拓寬數學思維的廣度

楊帆

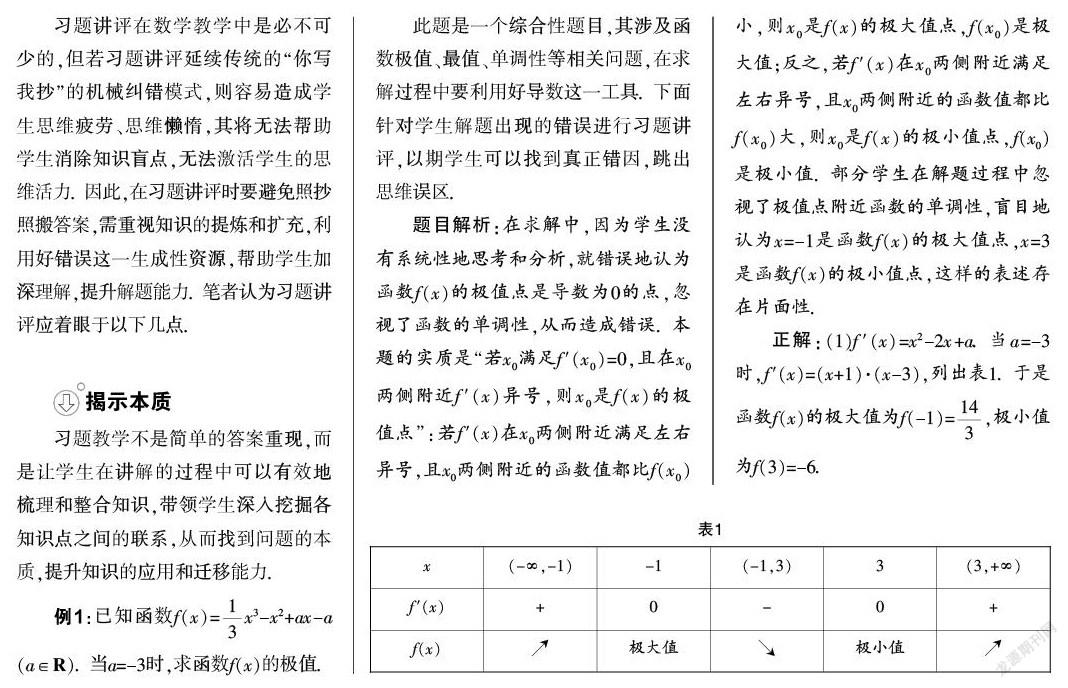
[摘 ?要] 科學的習題講評可有效地幫助學生深入理解知識，完善認知結構. 然而部分教師為追求習題教學的速度，常照搬答案，忽視對習題的提煉和挖掘，致使習題講評變成了簡單的糾錯. 若習題講評流于形式，則會限制學生的持續發展，因此習題講評應關注揭示問題的本質，重視數學思維和數學思想的培養，通過有效的鞏固練習來提升學生的解題能力.

[關鍵詞] 習題講評;持續發展;問題本質

習題講評在數學教學中是必不可少的，但若習題講評延續傳統的“你寫我抄”的機械糾錯模式，則容易造成學生思維疲勞、思維懶惰，其將無法幫助學生消除知識盲點，無法激活學生的思維活力. 因此，在習題講評時要避免照抄照搬答案，需重視知識的提煉和擴充，利用好錯誤這一生成性資源，幫助學生加深理解，提升解題能力. 筆者認為習題講評應著眼于以下幾點.

揭示本質

習題教學不是簡單的答案重現，而是讓學生在講解的過程中可以有效地梳理和整合知識，帶領學生深入挖掘各知識點之間的聯系，從而找到問題的本質，提升知識的應用和遷移能力.

本題的求解過程中充分展現了數形結合思想的優勢. 數形結合是解決函數問題的常用方法，因為其更加直觀和形象，更容易觀察題目隱含的條件，所以在解題時被廣泛使用. 從本題可以看出，采用數形結合方法求解，大大地降低了計算量，從而降低了運算出錯的概率. 數形結合是重要的數學思想，在日常的學習中要有意識地培養和訓練，這樣可以大幅度提升學生解決問題的能力和解決問題的效率.

升華認知

習題講評要著眼于整體和全局，要注意學習習慣的培養，注意引導學生從抽象的問題中總結歸納出通性通法，從而化難為簡，提高學生的數學應用能力.

1. 認真審題

題設條件和結論就是解題的主要信息來源，因此在解決問題前一定要認真審題，弄清楚每句話、每個條件、每個邏輯關系，通過找到知識點之間的聯系解決問題. 實踐證明，只有認真地審題，才能獲得更多的信息，才能從條件和結論中獲得啟發，找到解決問題的方向和方法.

2. 拓展思維

教師在習題講評中，在解同一個問題時要嘗試應用不同的方法，其目的有兩個：一是尊重個體差異. 因為不同學生的認知水平及思維方式有所不同，其思考問題及解決問題的方向也必然有所不同，通過多種方法進行講解可以滿足學生的不同需求，從而提高學生學習的興趣和信心. 二是拓展學生的思維. 在解題時學生常會受到固定思維的困擾，即使發現一些解法可以解題但仍然無法擺脫思維定式的束縛，通過多種方式的講解，可以培養學生從不同角度觀察及解決問題的能力，提升思維的變通性和廣闊性.

3. 歸納總結

在高考題目中，壓軸題大多考核的是學生綜合應用知識的能力，若想在高考中取得好成績，就需要在日常教學中培養學生學會總結解題方法和解題技巧，從而提升學生綜合應用知識的能力. 例如，前文舉例的幾個題目是含參不等式的取值問題，其更具探究性，也是壓軸題中常見的題型. 求解中應用了數形結合、分類討論、函數與方程等數學思想，主要考核的是學生如何利用已學知識將題目進行有效轉化，即將復雜的、不熟悉的問題轉化為易操作的、熟悉的問題，從而消除畏難心理，提升解題效率.

4. 鞏固訓練

教師在習題講評中需要為學生精心設計一些鞏固知識的練習題，使學生通過鞏固訓練強化自己的認知，升華解題方法和解題技巧. 例如，為了鞏固前文的學習成果，教師給出了如下題目以供學生進行鞏固訓練：

（1）已知三個函數：①f（x）=x3-3x;②f（x）=x3+3x;③f（x）=3x4-4x3. 請判斷函數的極值點個數后，分別畫出函數的圖像，并談一下自己的發現及感悟.

（2）已知函數f（x）=x3-ax2+ax. 實數a取何值時，函數f（x）在R上是增函數？若要使函數f（x）在R上有極值（極大值和極小值同時存在），求實數a的取值范圍.

習題講評中，教師設置了分層的鞏固訓練：問題（1），教師先讓學生通過已有經驗進行判斷，接下來通過圖形進行驗證，最后讓學生總結出發現問題的規律和自己的感悟. 在問題（1）解決之后，學生對極值的概念又有了深層認識. 在問題（1）的鋪墊下，學生求解問題（2）時也就顯得游刃有余了. 因個體差異的存在，有部分學生對解題方法的理解仍然局限于個別題目，適當的鞏固練習，可以讓其跳出固定題目的束縛，達到進一步鞏固和強化的目的，有利于解題水平的提升.

總之，在習題講評中，教師的目光不能局限于正確答案的求解過程，而應通過多方面的引導使學生形成良好的解題習慣. 同時應引導學生注意解題方法和解題技巧的積累，從而在特殊的、復雜的問題中找到一般的、簡單的解決方法，從而提升學生的解題能力.