立足教學細節,讓課堂教學精彩演繹

[摘 ?要] 教學細節是學生知識成長的營養劑,是學生知識發展的基石. 文章以“平行線的性質與判定”專題復習課為例,立足教學細節,以問題情境——問題探究——變式探究的路徑展開教學,促使不同的學生在數學上獲得不同的發展.
[關鍵詞] 教學細節;精彩演繹;問題;變式;平行線的性質與判定
新課程標準指出,人人要學有價值的數學,不同的人在數學上獲得不同的發展. 精彩的課堂是由許多閃光的細節組成的,也是通過細節來演繹的[1]. 如創設一個良好的學習氛圍,設置一個有啟發意義的情境,教師給予學生一個恰當的評價等. 教學細節是學生知識生長的營養劑,是學生知識發展的基石. 近期,筆者立足教學細節,上了一堂專題復習示范課——“平行線的性質與判定”,現整理出來與大家分享.
“平行線的性質與判定”教學 實錄
課前,筆者打開PPT,第一頁上顯示了課題:平行線的性質與判定;主講老師姓名:張宇蕾.
師:同學們,你們知道老師姓什么嗎?
眾生回答:姓張,張老師.
師:既然同學們都認識我了,我也想認識認識大家,誰愿意介紹下自己,并說說自己的興趣愛好呢?
有幾位學生都很自信地介紹了自己,說出了自己的興趣愛好,然后有一位學生慢吞吞地站起來說:我喜歡打籃球,但是數學不怎么會.
(此時班里有幾位學生在偷笑)
師:不會沒有關系,到學校來就是要學習不會的東西.
后面又有幾位學生介紹了自己,直到上課鈴響.
利用課前的幾分鐘時間,筆者與學生進行了親切的互動,增進了彼此的了解,與學生進行了情感交流,增進了師生之間的感情.
1. 問題情境
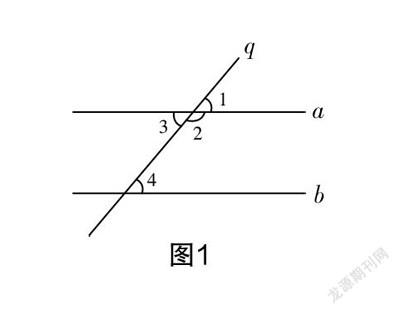
如圖1所示,直線q與直線a、b分別相交,你認為圖中相等的角有哪些?
創設與實際生活相關的問題情境是多數教師的引入方式,但是筆者一改大多數教師的做法,直接以平行線的具體圖形切入課堂,“單刀直入”地引入,能夠起到開門見山的作用.
生1:圖中可以看到相等的角,包括∠1=∠3,∠1=∠4,∠3=∠4.
師:對于這位同學的回答,同學們有什么異議嗎?
生2:圖1中并沒有給出直線a與直線b是平行關系,所以這些角不一定相等.
然后,教師在黑板板書:當a∥b時,∠1=∠4(兩直線平行,同位角相等);當a∥b時,∠3=∠4(兩直線平行,內錯角相等). 接著筆者提出:對于∠1=∠3,若沒有a∥b的條件,還成立嗎?
生3:仍然成立,對頂角相等,與直線a、b是否平行沒有關系.
師:如果a∥b,那么圖1中有哪些互補的角呢?
生4:互補的角有∠2+∠4=180°,∠2+∠3=180°,∠1+∠2=180°,但是∠2+∠3=180°及∠1+∠2=180°與兩直線是否平行沒有關系.
教師:為什么這么說呢?
生4:根據兩直線平行,同旁內角互補,得∠2+∠4=180°;根據鄰補角互補,得∠2+∠3=180°,∠1+∠2=180°.
教師繼續板書:當a∥b時,∠2+∠4=180°(兩直線平行,同旁內角互補).
2. 問題探究
如圖2所示,已知直線CD∥EF,點G是平行線外一點,那么∠C,∠E,∠G這三個角之間有何數量關系?并說明理由.
(學生先獨立思考,再小組合作交流,教師在教室內巡回指導,與學生互動)
生5:因為CD∥EF,根據兩直線平行同位角相等,得∠1=∠E,因為∠1是三角形的一個外角,根據三角形外角的性質,得∠1=∠C+∠G,所以∠C+∠G=∠E.
生6:還可以利用內錯角相等來說明. 因為CD∥EF,根據兩直線平行內錯角相等,得∠2=∠E,因為∠2是三角形的一個外角,根據三角形外角的性質,得∠2=∠C+∠G,所以∠C+∠G=∠E.
生7:還可以利用同旁內角互補進行說明. 因為CD∥EF,根據兩直線平行同旁內角互補,得∠3+∠E=180°,根據對頂角相等,得∠3=∠4,根據三角形內角和定理,得∠4+∠C+∠G=180°,所以∠3+∠C+∠G=180°,所以∠C+∠G=∠E.
3. 變式探究
師:針對剛剛提出的問題,同學們回答得很精彩,現在請同學們發揮自己的聰明才智,提出一個問題來考考其他同學.
生8:如圖3所示,已知CD∥EF,且∠E=80°,那么∠1的度數是多少?
生9:如圖4所示,已知CD∥EF,延長CG得到∠1,且∠C=40°,∠1=160°,求∠E的度數.
兩分鐘后,沒有同學再提出問題.
師:同學們的問題都很有創意!如果去掉“如圖”兩個字,那么圖中點G的位置可能有哪些情況呢?大家可以在練習本上畫一畫,看能畫出幾種情況?兩分鐘后與大家分享.
學生畫出了點G可能存在的6種情況,如圖5所示.
師:當點G在圖5(1)的位置時,如何作輔助線尋找∠C,∠E,∠G這三個角的數量關系呢?
生10:延長DC與GE交于點P.
生11:過點G作GH∥CD
生12:連接CE.
師:三位同學分別從不同的角度解決了同一問題,值得大家借鑒.
“平行線的性質與判定”教學感悟
學生是課堂真正的主人,課堂教學的細節也是從學生的角度展開. 這堂課給學生營造了一種和諧的對話氛圍,筆者以自己的行動告訴學生要學會尊重、學會傾聽,當學生犯錯時,應給予鼓勵與引導.
1. 生活細節的情境創設
課前,筆者營造了輕松和諧的課堂氛圍,增進了師生關系,也為上課做好了充分的準備. “信其師才能信其道”,當學生說數學不怎么會時,筆者親切的言語給了學生莫大的鼓舞. 在講課伊始,筆者設置了一個結論開放的問題,當學生回答出現失誤時,讓其他學生來糾錯,接著給出平行條件,讓學生探究互補的角,使其真正成為學習的主人.
2. 委婉巧妙的細節提問
恰到好處的提問可以激發學生的興趣,啟迪學生的智慧,調節課堂氛圍[2]. 學生通過筆者巧妙的問題,能夠發現自己學習上的不足與優點,從而發揚優點修補缺點. 教育家陶行知曾言:“發明千千萬,起點是一問. ”筆者的提問為學生樹立了榜樣. 尤為值得一提的是,課上筆者讓學生自行提出問題,能放能收,當沒有學生提問時,及時地從預設中拿出問題,讓提問不斷充實著課堂.
3. 科學細節的教學評價
在數學課堂教學中,對學生的回答做出恰當的評價,需要教師有良好的素養與教學機智,不僅要做到客觀公正,而且要做到評價多樣化[3]. 本節課中,對于不同水平的回答,筆者給出的評價也是不同的,有的用語言,有的用手勢,有的用眼神,有的用拍肩. 當學生的回答不完整時,筆者耐心地幫助學生一起完成,這樣既解決了問題,也保護了學生的自尊心.
參考文獻:
[1]黃厚忠,劉新春. 在教學設計細節中體悟“數學味”[J]. 中學數學月刊,2020(12).
[2]孫偉剛. 例談數學課堂教學細節的缺失與跟進[J]. 云南教育(中學教師),2020(10).
[3]吳小兵. 重視教學細節,彰顯教學深度[J].中小學數學(初中版),2020(Z2).
3671501908294

