空間連續型機器人自適應魯棒容錯控制

邱小璐，蔡志勤*，劉忠振，彭海軍，，吳志剛

(1.大連理工大學 工程力學系，大連 116024； 2.大連理工大學 工業裝備結構分析國家重點實驗室，大連 116024)

1 引 言

隨著空間技術的蓬勃發展，空間機器人已經開始承擔并完成一些有難度的空間任務，如空間太陽能電站的構建、航天飛船燃料的加注和空間設備的安裝等。與傳統空間機器人不同，空間連續型機器人具有良好的彎曲特性和較強的靈活性，能更好地在非結構、狹窄和有限的工作空間內完成航天器或星上設備的故障檢測及維修等精細在軌服務任務，也可以通過自身的主動彎曲變形，完成對失效衛星的捕獲和回收，這些都使其具有更廣泛的應用前景和更高的研究價值，其動力學與控制問題已經成為研究熱點[1-3]。

相比傳統空間機器人，空間連續型機器人具有高度非線性的特點，加上空間機器人工作環境復雜，機器人自身存在參數攝動[7-9]、外部干擾[10]和測量噪聲，基于力學原理的建模[4-6]往往不能完全精確描述其動態特性，給控制器的設計增加了難度。Zhao等[1]通過時延估計技術來預測模型輸出，基于低精度模型實現了連續型機器人的位置控制。Chen等[10]使用RBF神經網絡逼近動力學模型，采用快速終端滑模提高了控制器收斂速度。Li等[11]采用卡爾曼濾波器實現了基于無模型的控制，降低計算負荷提高控制性能。

空間機器人在長期作業的情況下，頻繁的工作會導致其執行器發生故障，若是不能及時處理，會導致系統控制性能下降，甚至發生不可估計的后果。同時，空間機器人一旦執行器發生故障，缺少地面支持，極難維修。因此，提高空間機器人的容錯能力使得控制系統具有較高的可靠性，也是在軌服務急需解決的問題。雷榮華等[12,13]采用神經網絡分別補償空間漂浮基機器人的模型參數攝動和估計執行器的有效因子，設計了自適應分散容錯算法，兩種算法均未考慮存在不確定外部擾動時控制器的魯棒性。畢偉等[14]采用自適應律估計擾動上界，結合反步法，實現地面剛性機械臂的軌跡跟蹤，但該方法未對模型參數攝動進行研究。

基于此，本文提出自適應魯棒容錯控制器解決空間連續型機械臂系統三臂節執行器并發故障時的軌跡跟蹤問題。與上述研究采用神經網絡或自適應律估計故障或擾動下界[13,14]不同，本文采用自適應神經網絡調節滑模控制器的切換項增益，設計的滑模切換項用來抑制故障因子、模型參數攝動和外部擾動，這些都使得控制器具有較強魯棒性的同時也滿足了控制要求。

2 空間機器人動力學模型

基于等曲率假設，建立三臂節空間連續型機器人系統的動力學模型。連續型機器人幾何位形為平面運動，如圖1所示。αk(k=1,2,3)為第k臂節的彎曲角度，θk為Ok-XkYk相對于O-XY的轉角，(xk,yk)T是Ok在O-XY的坐標。

選取系統廣義坐標

q=[α1,α2,α3]T

(1)

空間連續型機器人系統動能T由節盤動能Td和柔性支撐動能Ts組成。

(2)

式中M為系統的質量陣。

連續型機器人系統彈性力Qe的虛功為

(3)

式中E為柔性支撐的彈性模量，A為其截面面積，l為其長度，ε為彎曲應變，s為力作用點到局部坐標系原點的弧長。

連續型機器人系統驅動力Qa的虛功為

(4)

與速度二次項有關的廣義力Qv為

(5)

空間連續型機器人系統動力學方程為

(6)

考慮執行器故障為乘性故障，將驅動力τ=[τ1,τ2,τ3]T分離，可以得空間連續型機器人系統動力學方程

(7)

考慮模型參數攝動和外部擾動的空間連續型機器人系統動力學方程為

(8)

(9)

式中ΔM和ΔC為模型參數不確定項，d(t)∈R3 × 1

圖1 連續型空間機器人系統幾何位形

為外部干擾項。

3 空間機器人容錯控制算法設計

假設2p(t)有已知上界，即

定義快速非奇異滑模面為

(10)

U=-[sTG]T/‖sTG‖2‖s‖‖G‖

(11)

式中I3∈R3 × 3為單位陣。

為了保證閉環系統的運動在有限的時間內到達滑模面，非奇異快速終端滑模控制律如下，

τ=τ0+u0+u1

(12)

(13)

(14)

(15)

式(13，14)為等效控制律，當無模型參數攝動和外部干擾即p(t)=0時，可以單獨實現對期望軌跡的跟蹤控制，式(15)為切換項，p(t)≠0時，用來抵消由模型參數攝動和外部干擾引起的跟蹤誤差。

利用自適應RBF神經網絡來估計b0,b1和b2為切換項增益，并自適應調節網絡權值的更新。

三個RBF神經網絡的輸入和輸出分別為

(16)

(17)

由此，基于自適應神經網絡的終端滑模控制律的切換項為

(18)

4 穩定性分析

定理1 對于動力學方程(3)，控制律(7)確保位置誤差在有限時間內收斂到0。

證明 結合式(8)求取誤差動力學方程有

(19)

將式(13,14)代入式(19)，有

(20)

由式(14)構造

(21)

選擇Lyapunov函數如下

(22)

式中Γ0，Γ1和Γ2為正定矩陣。

對式(22)求取一階導，有

(23)

將式(13,16)代入式(23)，根據假設3有

(24)

三個網絡權值自適應更新律為

(25)

5 仿真算例

對圖1所示三臂節空間連續型機械臂系統，在Matlab中，采用四階-五階龍格-庫塔求解器進行動力學求解，采樣步長為0.01s(單位s)。通過三個算例驗證本文算法的有效性。

機械臂物理參數選取如下，節盤質量和半徑分別為md=0.01 kg，r=3.02×10-2m，柔性支撐長度和質量分別為l=0.6 m，ms=0.01 kg，彈性模量和截面慣性矩分別為E=1.67×104N·m-2，I=1.92×10-12m4。

RBF神經網絡的徑向基函數選取如下，

(m=1,2,…,7,i=0,1,2)(26)

式中bm為徑向基函數基寬向量，cm i為中心向量，網絡隱含層節點數目為7。

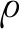
圖2為空間連續型機器人三臂節的跟蹤誤差曲線。可以看出，兩種算法都能在容錯的同時實現軌跡跟蹤控制。本文提出的控制自適應跟蹤控制算法可以實現在8 s，5.5 s和4 s時，跟蹤誤差收斂到0，比文獻[13]的控制算法收斂速度快，超調量小。5 s后，兩個控制器的跟蹤精度和速度都有較好的表現。

表1 控制器參數

圖2 無干擾下常值期望跟蹤誤差曲線

算例2仿真采用與算例1相同的有效因子,系統初始位置為(0.17 rad,0.17 rad,0.17 rad)，控制參數列入表2。在0 s～5 s內，對三臂節均施加常值干擾；在5 s～10 s內，對第二臂節施加干擾sin(q2)；在15 s～20 s內，對第三臂節施加干擾sin(q3)，其余時刻干擾為0。三臂節彎曲角度的期望軌跡如下,

qd 1=(π/18)sin[(π/9)t]+π/8

qd 2=(π/18)sin[(π/9)t]+π/7

qd 3=(π/18)sin[(π/9)t]+π/6

圖3驗證了本文算法對擾動和模型參數攝動的抑制能力。可以看出，兩種算法都能完成跟蹤任務。第二臂節在5 s～10 s內受到時變干擾，與文獻[13]相比，本文算法的跟蹤誤差基本收斂。這說明本文算法對外部擾動和參數攝動具有更強的抑制能力。同時本文算法也在5 s，3 s和2 s內完成了軌跡跟蹤任務，具有更快的收斂速度。

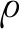
本算例采用了較小的有效因子來驗證本文算法的容錯能力。圖4表明，當故障較嚴重時，在 5 s～10 s內，第二臂節受到時變干擾，文獻[13]算法的跟蹤誤差曲線并未完全收斂，本文算法在實現跟蹤誤差收斂的同時，控制器具有更快的收斂速度和更小的超調量，即具有更好的動態性能，控制器保持較強的魯棒性。

表2 控制器參數

圖3 干擾下時變期望跟蹤誤差曲線

圖4 干擾下時變期望跟蹤誤差曲線

6 結 論

針對空間連續型機器人系統三臂節執行器并發故障的情況，提出一種自適應魯棒容錯控制算法。采用快速非奇異終端滑模控制器，同時通過神經網絡自適應調節控制器的切換項增益，實現空間連續型機器人的軌跡跟蹤控制。

仿真驗證了控制器的有效性和對模型參數攝動和外部干擾的抑制能力。結果表明，本文提出的控制器優點如下。非奇異快速終端滑模避免了計算奇異現象；本文采用自適應神經網絡調節切換項增益，與文獻[13]相比，對于常值型和時變型兩種軌跡，本文都具有更高的跟蹤精度和更快的跟蹤速度；與文獻[13]相比，本文所設計的切換項可以更有效地抑制模型參數攝動和外界干擾，具有更強的魯棒性。在后續工作中，可以在此基礎上解決執行器與傳感器同時發生故障的容錯控制問題。