求解大柔度梁/繩索的ANCF單元及隱式迭代格式

羅 鑫，魏泳濤

(1.四川大學 建筑與環境學院，成都 610065; 2.四川中銳信息技術有限公司，成都 610094)

1 引 言

繩索結構應用廣泛，如太空中的系留衛星系統(Tethered Satellites System)[1,2]、海洋船舶工業、核工業和機場等領域內的橋式起重機(Overhead Cranes)[3,4]以及高速列車系統中的懸鏈線(Pantograph/Cantenary)[5]等。彈簧-阻尼-集中質量模型[6-8]是數值模擬繩索的常用方法，但該法的繩索處理成分段折線而不再保持光滑曲線的形態，因而精度較低。有限元法在分析繩索時[9,10]，通常采用具有極低抗彎剛度或大柔度的梁單元以保證其形態的光滑性。在繩索運動中，往往存在大范圍剛體運動和大變形的耦合作用。但傳統梁單元的節點自由度僅反映變形的撓度和轉角，即單元的剛體運動和變形是解耦的。浮動坐標法[11]將繩索運動考慮成隨浮動坐標系的大范圍運動與相對于浮動坐標系的變形的疊加，但由此導出的科氏力和向心力等慣性力表達式十分復雜。

為克服浮動坐標法中的難點，Shabana[12]提出了以節點坐標和斜率作為節點自由度的絕對節點坐標方法ANCF(Absolute nodal coordinate formulation)。該方法的基本思想為在連續介質力學中對即時構形進行物質描述時，運動和變形本身就是耦合的。因此，若將梁/繩索的節點坐標和斜率而非節點撓度和轉角設置為節點自由度，則可自動耦合大范圍運動和大變形，也無需單獨考慮科氏力和向心力等慣性力，且質量矩陣是常數矩陣。 ANCF 已有關于繩索的研究，Gerstmayr等[13]將標準梁單元的自由度減少并引入附加的形函數，構造了低階的空間兩節點繩索單元；Seo等[14]使用該單元模擬了高速列車系統接觸網的三維大變形問題；Shan等[15]使用無抗彎剛度的該單元分析了太空中的系留網。

ANCF中單元的節點等效力計算遠比傳統有限元復雜。劉鋮等[16]基于第一類Piola-Kirchhoff應力張量導出了節點等效力及雅可比矩陣的解析表達式。范紀華等[17]在節點等效力求解中引入了彈性線方法。Gerstmayr等[13]逐一計算了節點等效力各元素，特別是對應于彎曲變形的情況。Zemljaric等[18]對節點等效力計算方法進行了一定簡化。Berzeri等[19]推導了小變形下歐拉-伯努利梁單元的節點等效力。這也是目前ANCF分析繩索時采用顯式積分的主要原因。顯式積分不需要迭代，既避免了不收斂的問題，也免去了由節點等效力導出切線剛度矩陣的繁瑣過程，但必須按算法的穩定原則確定足夠小的時間步長。而隱式積分在各時間步上需迭代求解以滿足平衡方程，在采用較大時間步長時也能保證精度要求。

由節點等效力導出隱式積分所需的的切線剛度矩陣，目前尚無此方面完整研究的報道。此外，基于ANCF方法分析繩索時，多針對單根繩索，而對工程中常見的多根繩索系于一點的情況，還未有考慮。本文對ANCF大柔度梁/繩索單元，導出了用于平衡迭代的切線剛度矩陣的全部公式；其關鍵環節在于將兩矢量的叉乘表示為反對稱矩陣與矢量的點乘，以此改造ANCF大柔度梁/繩索單元的節點等效力公式；由此導出的節點等效力和切線剛度矩陣均為矩陣形式，也非常方便代碼開發；對不同ANCF單元的鉸接和剛性連接，引入罰方法的處理；最后結合HHT(Hilber-Hughes-Taylor)隱式格式，對弦微幅和小幅振動、雙桿擺和T字形桿以及柔繩進行了數值模擬。

2 基于ANCF的大柔度梁/繩索單元

研究細長的等截面大柔度梁/繩索，在運動/變形中始終維持光滑曲線，且橫截面是正多邊形，即橫截面對通過形心的任何軸都具有相同的慣性矩。本文基于文獻[13]提出的2節點12自由度的ANCF梁/繩索單元，該單元服從平截面假設，不考慮剪切變形和扭轉變形。當單元具有極低或零抗彎剛度時，即可用于繩索模擬。

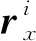
r=[S1IS2IS3IS4I]e=Se

(1)

式中I為3×3的單位陣,S1～S4為埃爾米特插值基函數,e為將節點i和j處的位置矢量和切線矢量排列而得的單元自由度向量。

(2)

Sx,Sx x,rx和rx x為相應的一階和二階導數。

單元慣性力在虛位移δr上的虛功為

(3)

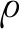
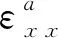
(4)

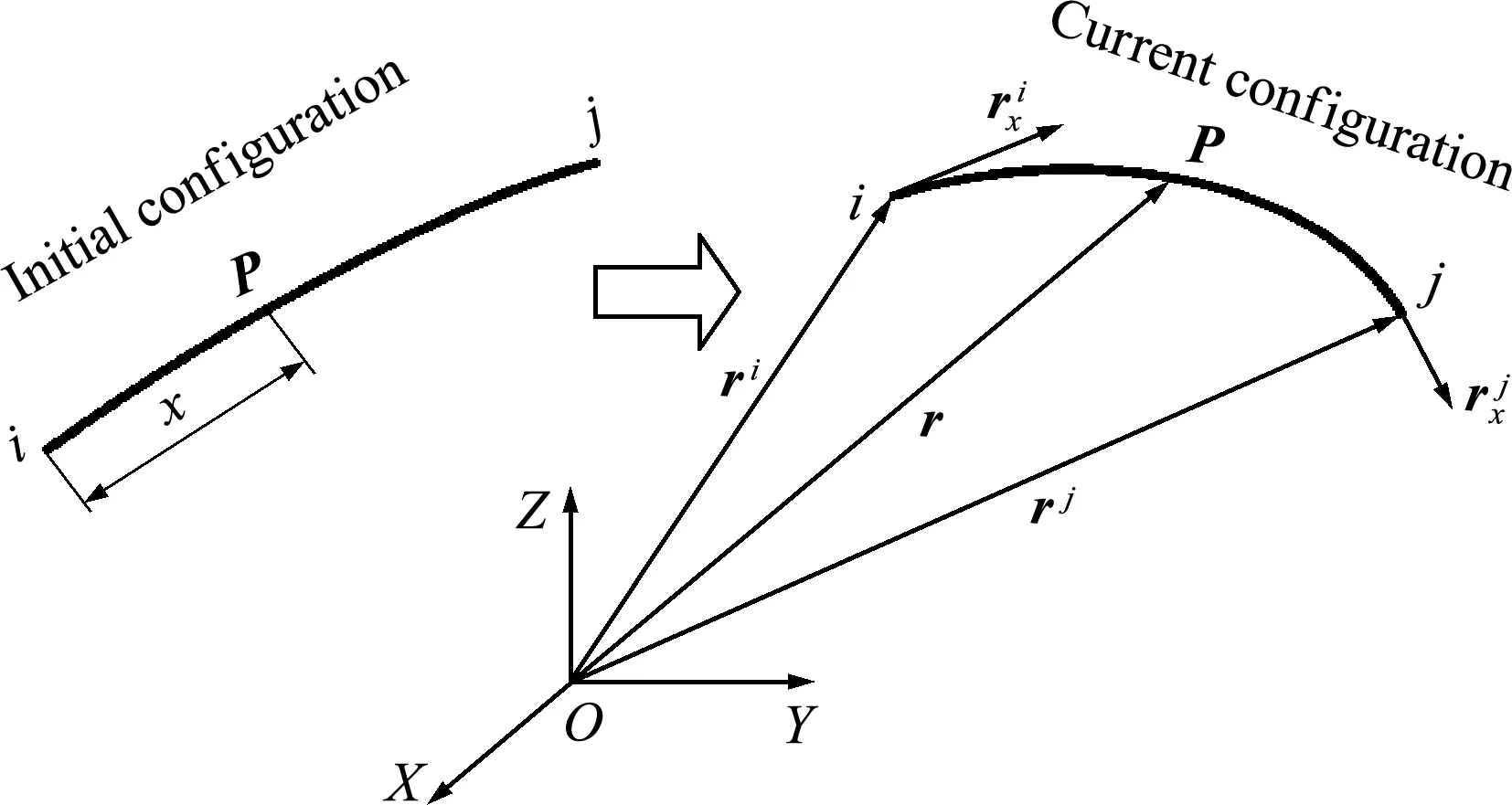
圖1 單元內任一點P的位置的插值

由歐拉-伯努利梁理論，單元內力的虛功為

(5)

為簡化書寫，記矢量c=rx×rx x。將矢量叉乘運算改寫為矩陣乘積： -rx x×rx=Grx,rx×rx x=Qrx x,c×rx=Rrx;G,Q和R為反對稱矩陣，對偶矢量分別為-rx x,rx和c。

(6)

(7)

(8)

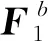
3 隱式動力學迭代格式

為將隱式積分格式應用于前述建立的ANCF大柔度梁/繩索單元，需建立平衡迭代格式，為此應從節點等效力導出相應的切線剛度矩陣。

采用HHT隱式時間積分方法建立繩索的隱式動力學迭代格式，根據HHT方法，

(1+α)Ft + Δt-αFt-Pt + (1 + α)Δt=0

(9)

(10)

(11)

式中Ψ為不平衡力向量，C為阻尼矩陣，P為等效外載荷。

當積分參數滿足-0.3≤α≤0，β=0.25(1-α)2，γ=0.5-α時，HHT方法是無條件穩定的。其中α=0時，HHT退化成β=0.25，γ=0.5的Newmark法，該方法的主要缺點是無法濾掉虛假的高階分量。

動力學切線剛度矩陣(即迭代中的雅可比矩陣)為

(12)

(13)

(14)

(15)

(16)

此處略去切線剛度矩陣繁瑣的推導過程。由此在t+Δt時刻的Newton-Raphson迭代格式為

(17)

需要注意的是，HHT法在單元過程中要單獨計算上一時刻應力的節點等效力，且外載荷是t+(1+α)Δt時刻的。

4 鉸接和剛性連接的處理

ANCF大柔度梁/繩索單元使用切線的斜率為自由度，在剛性連接中，連接處的節點具有不同的切線方向，因此應作特別處理。

如圖2所示，節點i和節點j分別鉸接或剛性連接，約束方程為

(18)

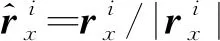
圖2 鉸鏈和剛性連接

(19)

(20)

式中0為3×1的零矢量或3×3的零矩陣，C1和C2是罰因子，即相應的彈簧剛度。本文算例表明，可分別取為拉伸和彎曲切線剛度矩陣最大元素的1000倍。切線剛度矩陣第三項的推導中考慮矢量模的倒數為常數，從而簡化計算過程。

5 數值算例

5.1 弦的微幅和小幅振動

弦在張緊狀態下作橫向微幅振動時，內部張力可視為常數。圖3所示的弦，長為1 m，直徑為0.2 mm，彈性模量為200 GPa，密度為7800 kg/m3，兩端簡支，弦的張力T=5 N。初始時受外部約束而水平靜置，突然撤去外部約束后，弦在重力作用下發生微幅振動，其理論解為

(21)

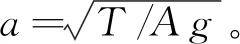
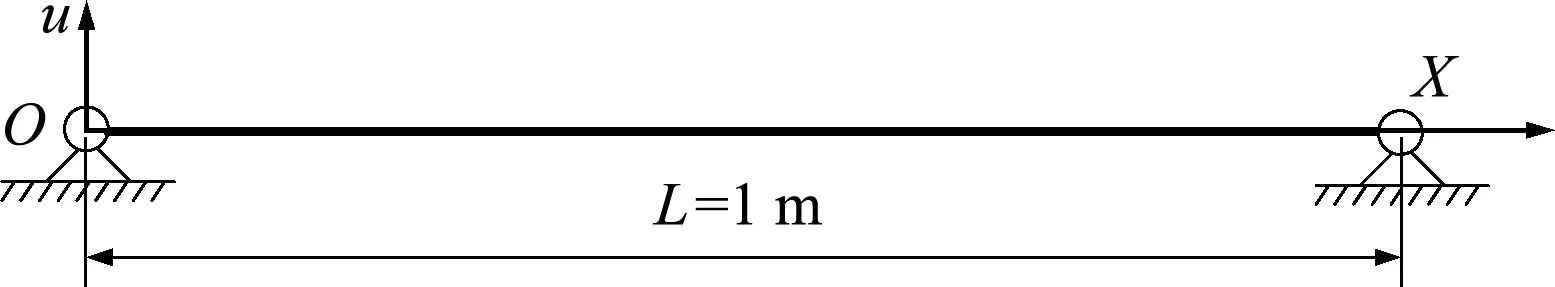
圖3 振動的弦

使用20個ANCF繩索單元模擬，HHT中積分參數α取為-0.005，時間步長取為10-4s。圖4是弦中點橫向位移的理論解(21)與ANCF數值解的對比(每30個時間步輸出一個結果)。弦中點的最大振幅為0.1201 mm，符合微幅振動的假設。模擬結果與理論解符合得很好。

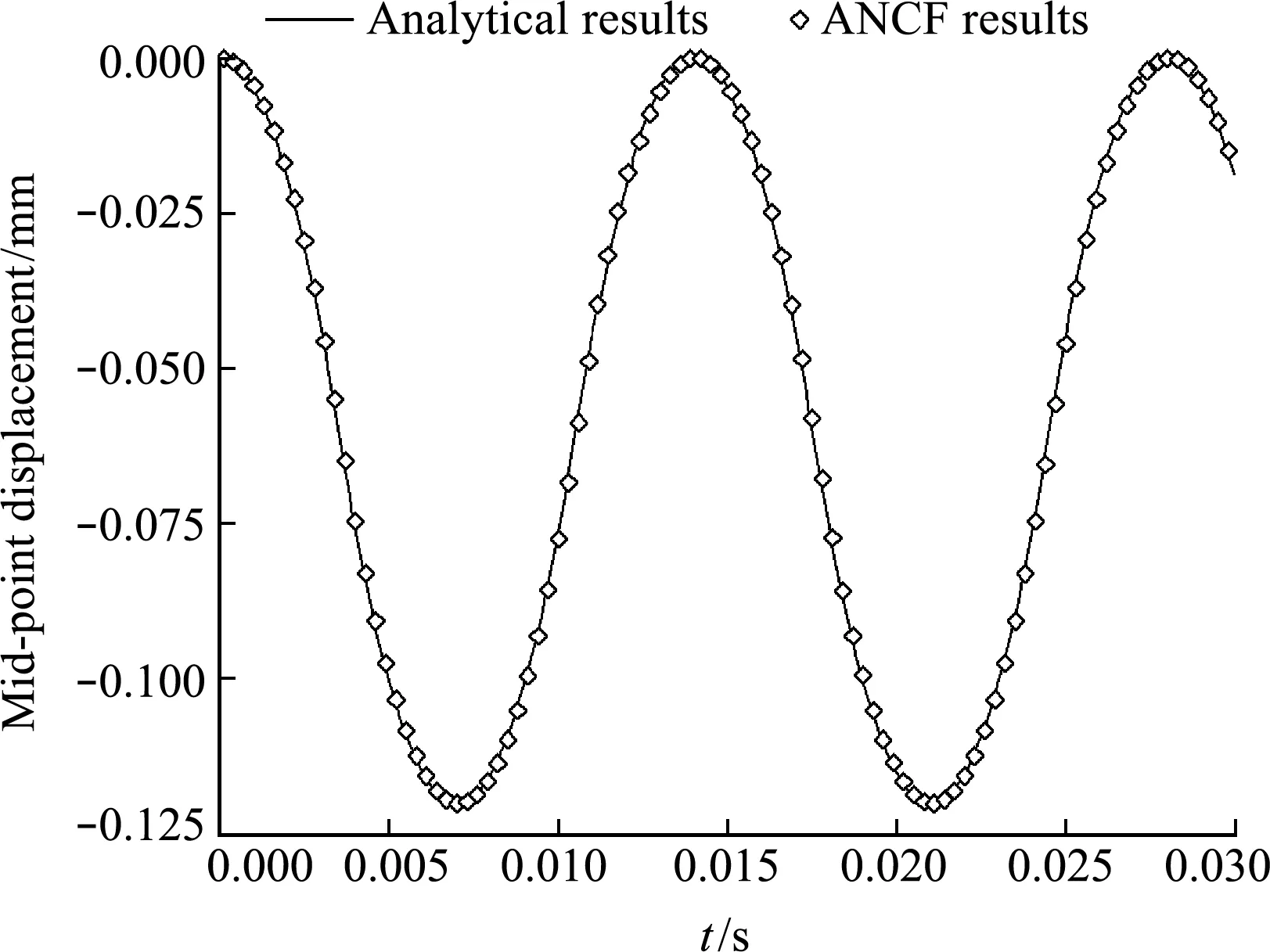
圖4 中點位移的對比

進一步考察在弦中點受沖擊載荷作用下的響應，載荷為0 s ～0.02 s內一幅值Q為1 N或10 N的三角形力波。由于未有該情況下的解析解，故將ANCF的數值解與ANSYS中采用三次插值模式的Beam188單元的結果進行對比。將弦均分為20個單元，ANCF采用α為-0.005得HHT格式，時間步長為10-4s；ANSYS采用Newmark格式，時間步長為10-5s。

圖5列出了在沖擊載荷幅值分別是1 N和 10 N 時，弦中點的位移時程，此時最大振幅分別超過了30 mm和65 mm，已不再符合微幅振動假設。ANCF數值結果與ANSYS結果符合得較好。

5.2 雙桿擺和T字形桿擺

為考察本文算法對于大剛度梁的模擬和約束處理，模擬圖6的直徑為2 cm的圓截面鋼梁，彈性模量為200 GPa，密度為7800 kg/m3，其中圖6(a)為兩根長為0.5 m的桿鉸接而形成的雙擺； 圖6(b)為T字形擺，各段長度均為0.5 m。均由水平位置無初速度釋放，各段等分為兩個單元，采用α為-0.005的HHT方法，時間步長均為10-3s。

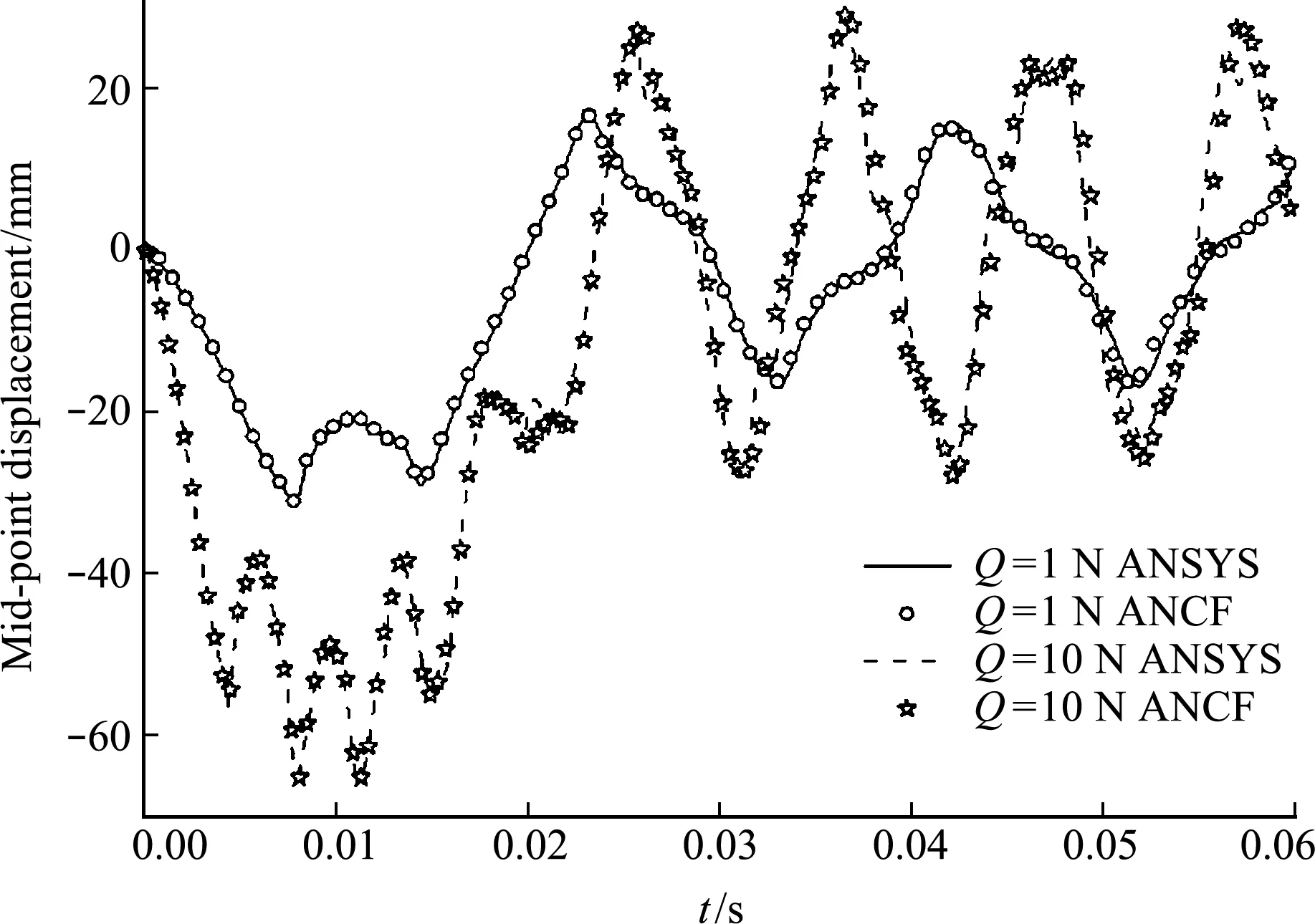
圖5 沖擊載荷下中點位移的對比

圖7為鉸接的兩個節點距離的時間歷程，距離越小表明約束效果越好，圖7列出了不同罰因子C1水平的模擬結果。罰因子0.01EA/L(L=1 m)時，鉸接節點的最大距離為94.07 μm，約束效果好。增大罰因子能達到更好的約束效果，但罰因子增大到1013EA/L會導致不收斂。

T字擺的模擬中，C1設置為103EA/L(L=1 m)，C2參照抗彎剛度EI/L進行設置。圖8為節點切線夾角θ0與直角之差的時間歷程。罰因子0.1EI/L能達到較好的約束效果，θ0與直角相差不超過1.5°，進一步增大罰因子至EI/L，θ0與直角相差不超過0.2°，但增大至100EI/L不收斂。

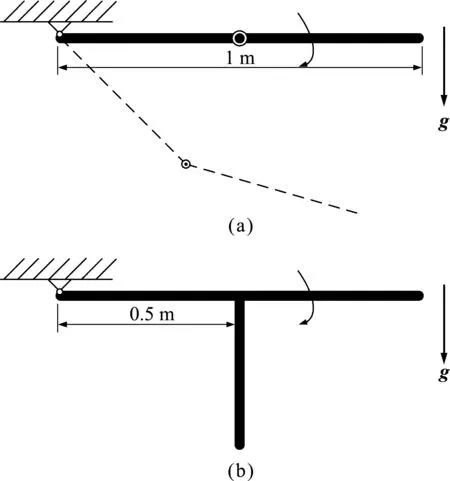
圖6 雙桿擺和T字形擺

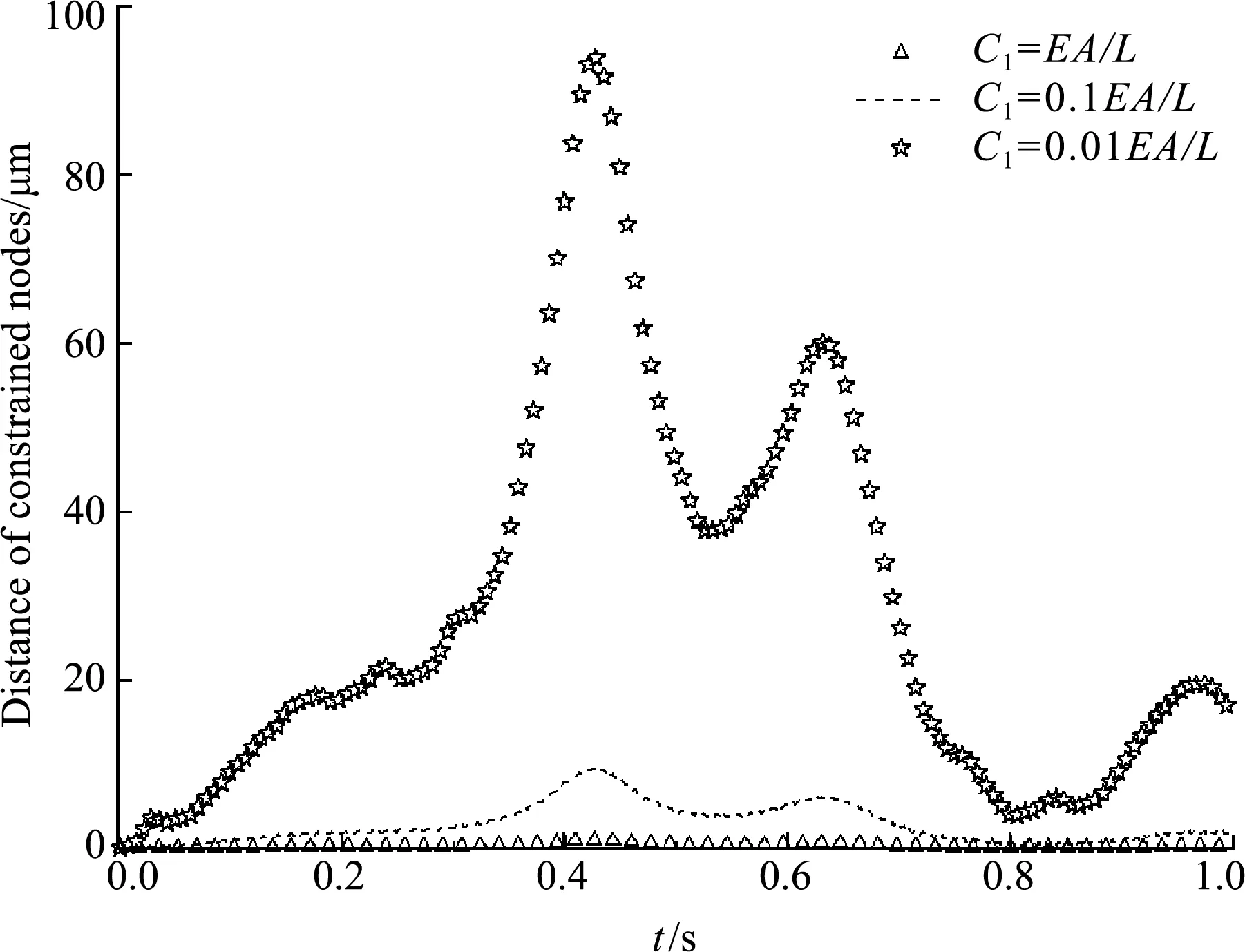
圖7 鉸接節點距離的時間歷程

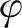
5.3 自由下落的柔繩

計算一根水平放置、左端鉸接于地面的柔繩，無初速度釋放，在重力作用下自由下落。繩長為 1.2 m，圓截面面積為0.0018 m2，截面慣性矩為 1.215×10-8m4，密度為5540 kg/m3，彈性模量為 0.7 MPa。

將模擬結果與已有結果[18]進行比較。節點等效力分別為小變形的Model I[19]、小/大變形的Model V[18]、符號運算的Model S以及本文的公式(6～8)。此前的算例采用四階龍格-庫塔法的顯式格式，本文算例采用HHT法的隱式格式，時間步長設置為10-3s。

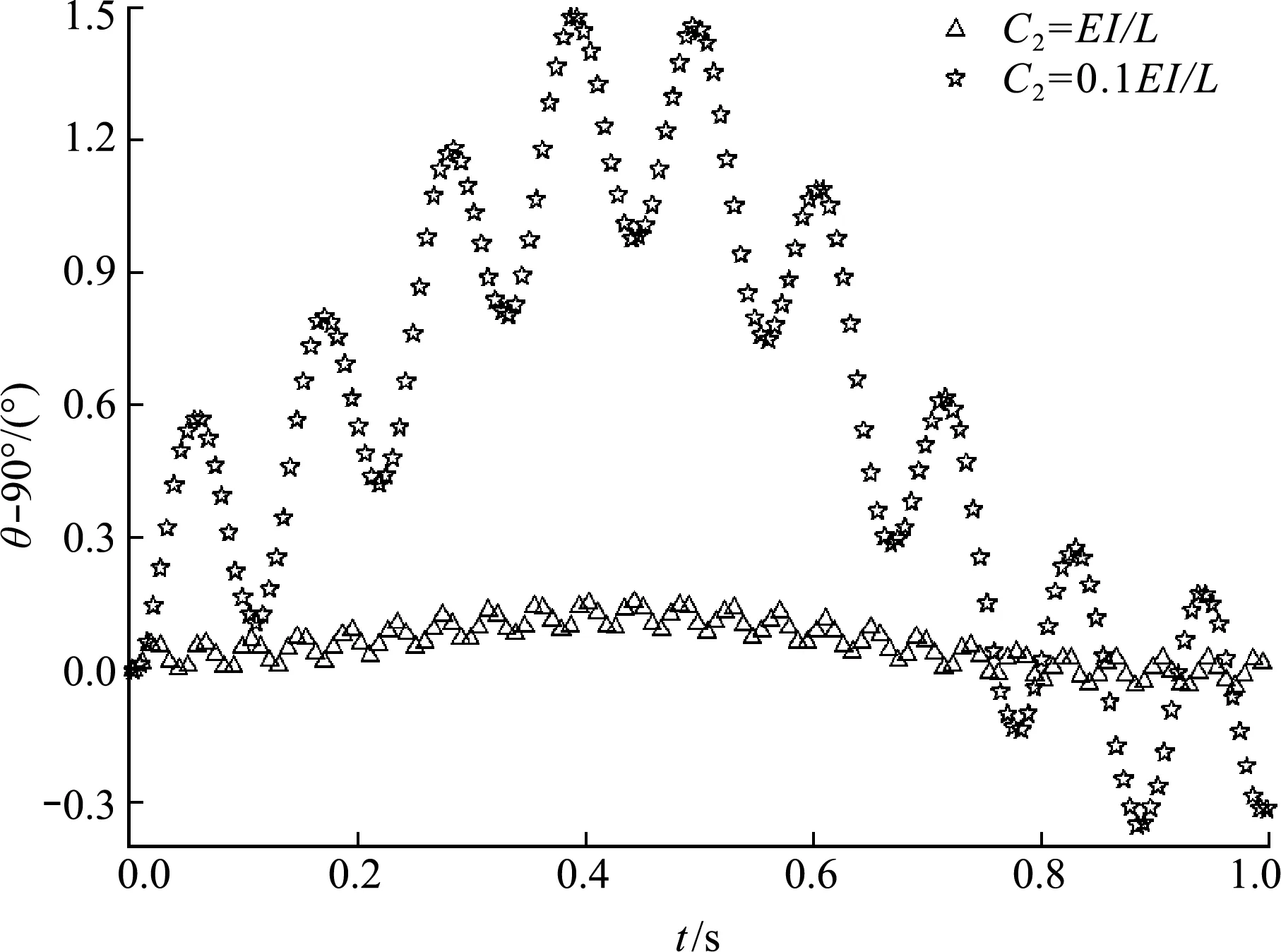
圖8 θ0和90°的對比

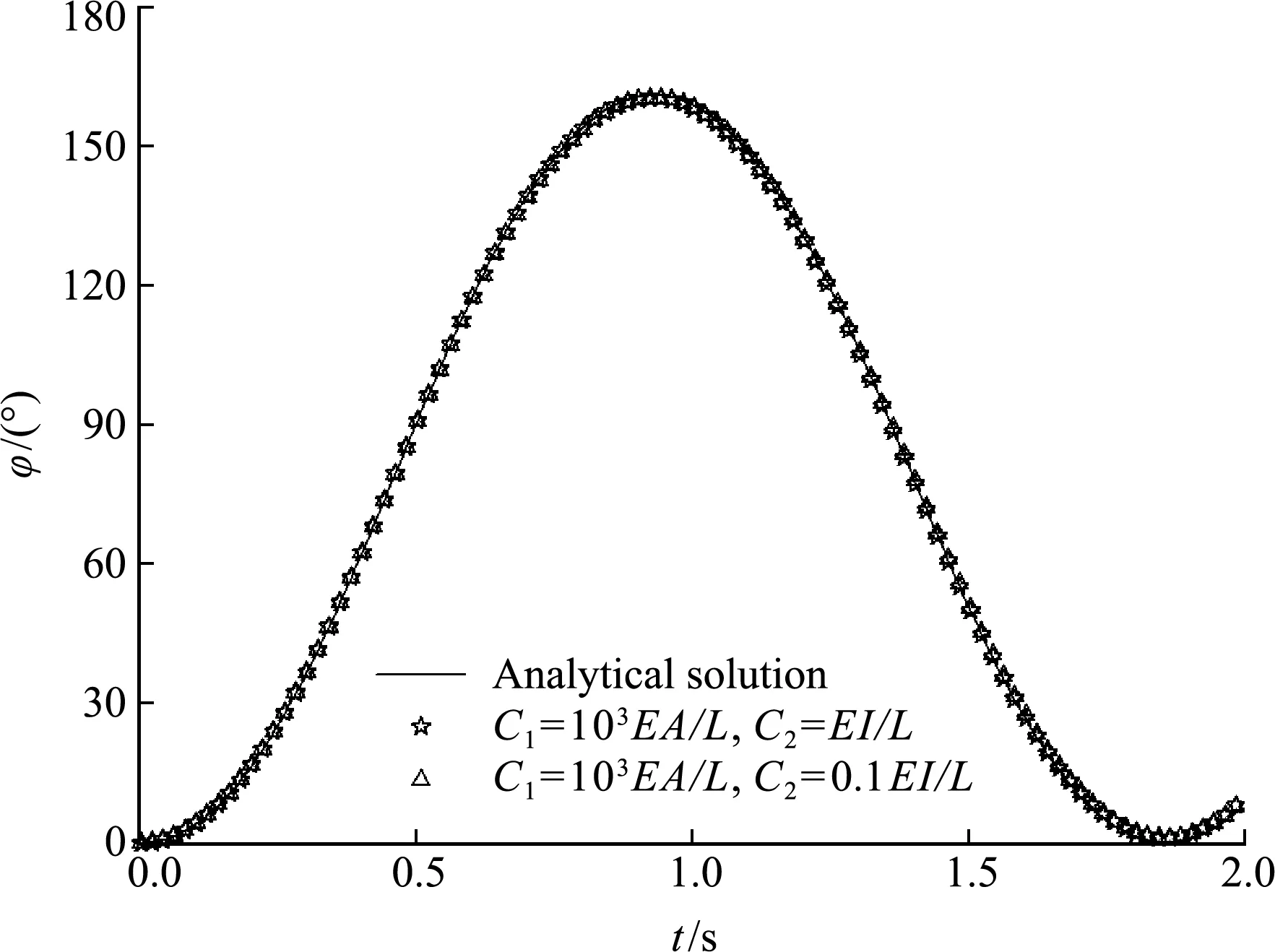
圖9 T字形桿擺動的ANCF結果和解析解

圖10是自由端鉛垂位置的時程曲線。本文算法的模擬結果與已有結果符合得較好，證明了本文公式及隱式迭代格式的正確性。考慮繩索水平釋放，在0.7 s時解除約束的情況，圖11為柔繩各時刻的形狀。

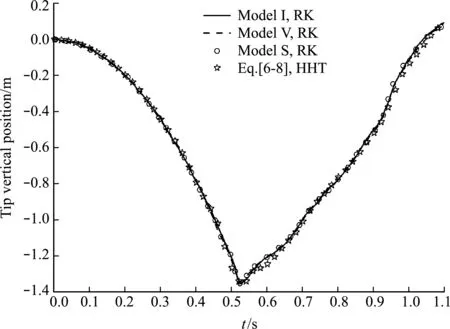
圖10 自由端的鉛垂位置

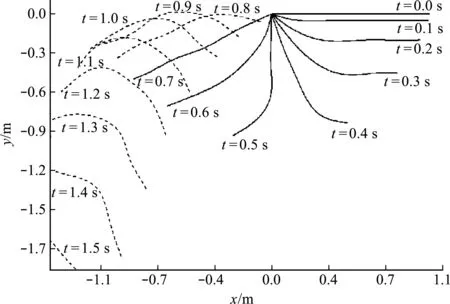
圖11 繩索各時刻的形狀

6 結 論

(1) 為有效模擬大柔度梁/繩索結構的大范圍運動和變形，針對ANCF大柔度梁/繩索單元建立了基于HHT方法的繩索隱式動力學迭代格式。

(2) 將矢量叉乘改寫為矩陣相乘，得到了 ANCF 大柔度梁/繩索單元的節點等效力公式，進一步由節點等效力導出了切線剛度矩陣的全部公式。

(3) 本文算法的模擬結果與理論解及已有結果符合得較好，驗證了節點等效力公式、切線剛度矩陣公式、及所建立的隱迭代格式的正確性。

(4) 采用罰方法處理ANCF的約束方程，實現了梁/繩索間的鉸接和剛性連接。數值模擬結果表明罰方法能夠有效實施此兩種約束。