對一道全國大聯考試題的拓展探究

福建省福州市閩侯縣第一中學(350100) 黃美琴

各類試題均是命題者集體智慧的結晶,含有豐富的數學內涵,具有可探究性和進一步拓展的空間,值得我們去深入探究.引導學生對一些典型的試題進行分析思考、多角度探究拓展,這對培養和提升學生的創新能力、數學學科核心素養無疑是有益的.正如美國數學家波利亞所說:“一個專心備課的教師能夠拿一個有意義的但又不太復雜的題目,去幫助學生發掘問題的各個方面,使得通過這道題,就好像通過一道門戶,把學生引進一個完整的理論領域”.下面是通過引導學生對一道全國大聯考試題進行的縱向、橫向和變式拓展.

題目(2020 屆高三全國第一次大聯評數學試題(理科) 第19 題)已知拋物線y2= 2x, 過點P(1,1)分別作斜率為k1,k2的拋物線的動弦AB,CD, 如圖, 設M,N為線段AB,CD的中點.(1) 略; (2) 若k1+k2= 1, 求證直線MN恒過定點,并求出定點坐標.

本題(2)的答案是直線MN恒過定點(0,1).本小題內涵豐富,意境深邃,具有拓展空間,值得我們引導學生進行適當的探究拓展.

1 縱向拓展: 由特殊到一般的拓展

對本題(2)的結論, 我們不禁要問: 對于一般的拋物線y2= 2px(p ＞0),定點P(m,n),k1+k2=λ(λ為常數),直線MN是否恒過某個定點? 經探究,可得

性質1.1已知拋物線y2= 2px(p ＞0), 過不在拋物線上的定點P(m,n)分別作斜率為k1,k2的拋物線的動弦AB,CD,設M,N為線段AB,CD的中點,若k1+k2=λ(λ為常數),則當λ= 0 時,直線MN的斜率k=(定值);當λ ?=0 時,直線MN恒過定點

證明設A(x1,y1),B(x2,y2),M(xM,yM),N(xN,yN),則相減并整理, 得·(y1+y2) =2p.又由條件知,y1+y2=2yM,則·yM=p,即+pm= 0.同理可得+pm=0.這表明點M,N的軌跡方程為y2?px ?ny+pm= 0.平移坐標軸, 把原點移至P(m,n),以x=x′+m,y=y′+n代入上式,得(y′+n)2?p(x′+m)?n(y′+n)+pm=0,即y′2?(px′?ny′)=0.設直線MN的方程為ux′+vy′=1,代入上式,使之成為關于x′、y′的二次齊次方程y′2?(px′ ?ny′)(ux′+vy′) = 0,整理得(1 +nv)y′2?(pv ?nu)x′y′ ?pux′2= 0, 化 為?pu= 0.易知直線AB(即PM),CD(即PN) 的斜率k1,k2為其兩根, 據韋達定理,得k1+k2=則當λ= 0 時,k1+k2=0?pv ?nu=0?直線MN的斜率k=(平移不改變直線的斜率); 當λ ?= 0 時, 有λ ?u(?n)+v(p ?nλ)=λ ??n)=1?直線MN恒過定點(在新坐標系中)?直線MN恒過定點(m ?)(在原坐標系中).證畢.

特別地,當p= 1,m=n= 1,λ= 1 時,直線MN恒過定點(0,1).這就是上述試題第(2)小題的答案.

2 橫向拓展: 由拋物線到橢圓、雙曲線的拓展

以上性質揭示了拋物線共定點的兩動弦中點連線的一個性質,那么,橢圓、雙曲線是否具有類似性質? 經探究,對于橢圓=1(a ＞b ＞0),有

性質2.1已知橢圓= 1(a ＞b ＞0), 過不在橢圓上的定點P(m,n)分別作斜率為k1,k2的橢圓的動弦AB,CD,設M,N為線段AB,CD的中點,若k1+k2=λ(λ為常數),則當λ= 0 時,直線MN的斜率k=(定值);當λ ?=0 時,直線MN恒過定點

證明設A(x1,y1),B(x2,y2),M(xM,yM),N(xN,yN),則相減并整理, 得又由條件知,x1+x2=2xM,y1+y2=2yM,則= 0.同理可得這表明點M,N的軌跡方程為b2x2+a2y2?b2mx ?a2ny= 0.平移坐標軸,把原點移至P(m,n),以x=x′+m,y=y′+n代入上式,得b2(x′+m)2+a2(y′+n)2?b2m(x′+m)?a2n(y′+n)=0.即b2x′2+a2y′2+(b2mx′+a2ny′)=0.設直線MN的方程為ux′+vy′=1,代入上式,使之成為關于x′、y′的二次齊次方程b2x′2+a2y′2+(b2mx′+a2ny′)(ux′+vy′) = 0,整理得b2(1+mu)x′2+a2(1+nv)y′2+(a2nu+b2mv)x′y′=0,化為

易知直線AB(即PM),CD(即PN)的斜率k1,k2為其兩根,據韋達定理得

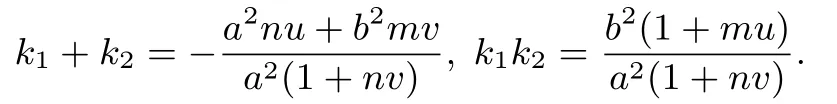
則當λ= 0 時,k1+k2= 0?a2nu+b2mv= 0?直線MN的斜率k=(平移不改變直線的斜率);當λ ?=0 時

?直線MN恒過定點(在新坐標系中)

?直線MN恒過定點(在原坐標系中).證畢.

對于雙曲線E:= 1(a ＞0,b ＞0),只要把上述證明中的“b2”替換為“?b2”,容易得到

性質3.1已知雙曲線E:= 1(a ＞0,b ＞0),過不在雙曲線上的定點P(m,n) 分別作斜率為k1,k2的雙曲線的動弦AB,CD, 設M,N為線段AB,CD的中點,若k1+k2=λ(λ為常數), 則當λ= 0 時, 直線MN的斜率k=(定值) ; 當λ ?= 0 時, 直線MN恒過定點

3 變式拓展: 由“k1+k2 =λ”到“k1k2 =λ”的拓展

以上性質揭示了拋物線、橢圓、雙曲線在“k1+k2=λ”條件下的共定點兩動弦中點連線的一個性質,如果把該條件變為“k1k2=λ”,會有什么相應的結論?

由性質1.1 的證明, 可得k1k2=若k1k2=λ(λ為非零常數),則=λ ?u·0+v(?p ?nλ)=λ ? u ·0 +?n) = 1?直線MN恒過定點?n)(在新坐標系中)?直線MN恒過定點)(在原坐標系中).由此可得

性質1.2已知拋物線y2= 2px(p ＞0), 過不在拋物線上的定點P(m,n)分別作斜率為k1,k2的拋物線的動弦AB,CD, 設M,N為線段AB,CD的中點, 若k1k2=λ(λ為非零常數),則直線MN恒過定點

由性質2.1 的證明, 可得k1k2=若k1k2=λ(λ為非零常數),則=λ ?u·b2m+v(?a2nλ)=a2λ ?b2.當λ=時,u·b2m+v(?a2nλ)=0?直線MN的斜率k=(平移不改變直線的斜率);當λ ?=時,直線MN恒過定點(在新坐標系中)?直線MN恒過定點(在原坐標系中).由此可得

性質2.2已知橢圓= 1(a ＞b ＞0), 過不在橢圓上的定點P(m,n) 分別作斜率為k1,k2的橢圓的動弦AB,CD, 設M,N為線段AB,CD的中點, 若k1k2=λ(λ為非零常數), 則當λ=時, 直線MN的斜率k=(定值) ; 當λ ?=時, 直線MN恒過定點

類似可得:

性質3.2已知雙曲線E:= 1(a ＞0,b ＞0),過不在雙曲線上的定點P(m,n)分別作斜率為k1,k2的雙曲線的動弦AB,CD, 設M,N為線段AB,CD的中點, 若k1k2=λ(λ為非零常數), 則當λ=時, 直線MN的斜率k=(定值);當λ ?=時,直線MN恒過定點

以上通過對一道全國大聯考試題的縱向、橫向和變式的探究拓展,得到了拋物線、橢圓和雙曲線的一類性質,揭示了問題的本質和規律.這確實是一道值得探究拓展的試題,正如著名數學教育家G·波利亞所形象比喻的:“好問題同某種蘑菇有些相像,它們都成堆地成長,找到一個以后,你應當在周圍找一找,很可能附近有好幾個.”對一些典型的試題,引導學生進行歸納、類比、聯想、發散等拓展探究,獲得一系列有價值的結論,這既是對原問題的深化與拓展,也是培養學生創新能力的有效途徑.經歷豐富多彩的充分探究,主動反思、合作交流等探究過程,學生的創造意識和創新思維能力以及數學學科核心素養就在不知不覺中得到培養和提升.