極值點偏移問題解題策略的探究

廣東省揭陽市第二中學(515500) 楊邦彬

圖1

1.如圖1, 假設函數(shù)f(x)的圖象的頂點的橫坐標(即極值點)為x0,若f(x) =c的兩根的中點剛好滿足=x0, 即極值點在兩根的正中間, 也就是說極值點沒有偏移.此時函數(shù)f(x)在x=x0(附近)兩側(cè)的函數(shù)值變化快慢相同.

圖2

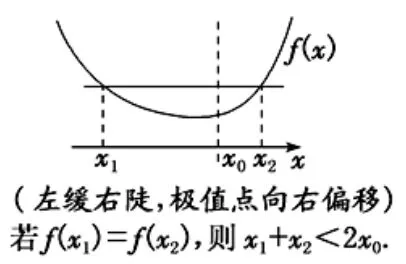
圖3

查閱有關文獻,在極值點偏移問題中,文[1]介紹極值點偏移的判定定理,并通過具體的例子介紹極值點偏移的解題方法;文[2]給出“和”型極值點偏移問題的統(tǒng)一解法;文[3]介紹了解決問題的四個步驟,讓學生能夠很好地按部就班進行邏輯推理.讓高中學生能夠理解與掌握解題的策略與通法,是極值問題教學值得研究的課題.為此,本文基于數(shù)學核心素養(yǎng)下學生審題能力提高的策略探究,把極值點偏移問題的解題策略歸納為三種題型進行探究: (1)對稱變換;(2)分離零點(極值點);(3)比(差)值換元.然后從引導學生運用導數(shù)研究簡單函數(shù)的性質(zhì)和變化規(guī)律、培養(yǎng)學生會用導數(shù)解決實際問題能力的視角,分類分析,循序漸進,一題多解,發(fā)揮學生的學習主動性,激發(fā)學生的學習動機,基于數(shù)學核心素養(yǎng)下, 探究歸納適合高中學生理解與掌握的有效策略與通法,提高學生的審題能力.

策略一 對稱變換

策略探究對稱變換,主要用來解決與兩個極值點之和相關的不等式的證明問題.其解題要點如下:

(1)定函數(shù)(極值點為x0),即利用導函數(shù)符號的變化判斷函數(shù)單調(diào)性,進而確定函數(shù)的極值點x0.

(2)構造函數(shù), 即根據(jù)極值點構造對稱函數(shù)F(x) =f(x)?f(2x0?x).

(3)判斷單調(diào)性,即利用導數(shù)討論F(x)的單調(diào)性.

(4)比較大小, 即判斷函數(shù)F(x)在某段區(qū)間上的正負,并得出f(x)與f(2x0?x)的大小關系.

(5) 轉(zhuǎn)化, 即利用函數(shù)f(x) 的單調(diào)性, 將f(x) 與f(2x0?x) 的大小關系轉(zhuǎn)化為x與2x0?x之間的關系,進而得到所證或所求.

提醒若要證明的符號問題,還需進一步討論與x0的大小,得出所在的單調(diào)區(qū)間,從而得出該處導數(shù)值的正負.

典例1(2016年高考新課標Ⅰ卷理數(shù)第21 題)已知函數(shù)f(x)=(x ?2)ex+a(x ?1)2有兩個零點.

(Ⅰ)求a的取值范圍;

(Ⅱ)設x1,x2是f(x)的兩個零點,證明:x1+x2＜2.

審題點撥本題待證不等式中含有兩個變量,對于此類問題的求解思路是通過兩個變量之間的關系“減元”,構造對稱函數(shù)F(x) =f(x)?f(2x0?x),然后根據(jù)函數(shù)的單調(diào)性,最終將問題轉(zhuǎn)化為函數(shù)的最值問題來求解.考查了邏輯推理、數(shù)學建模及數(shù)學運算等核心素養(yǎng).在求解此類問題時,需要注意變量取值范圍的限定,如本題中利用x1,2?x2的取值范圍,利用函數(shù)f(x)在(?∞,1)上的單調(diào)性來求解.

解題觀摩(Ⅰ)a的取值范圍是(0,+∞).(過程從略)

(Ⅱ)由(Ⅰ)知,函數(shù)f(x)在(?∞,1)單調(diào)遞減,在(1,+∞)單調(diào)遞增.令g(x)=f(x)?f(2?x)=(x ?2)ex+xe2?x,x ＞1,則2?x ＜1.所以g′(x) = ex+(x ?2)ex+e2?x ?xe2?x= (x ?1)(ex ?e2?x)＞0.所以g(x)在(1,+∞)單調(diào)遞增, 所以g(x)＞g(1) = 0.不妨設x1＜1,x2＞1, 則g(x2)＞0, 即f(x2)＞f(2?x2), 因為f(x1) =f(x2), 所以f(x1)＞f(2?x2),因為函數(shù)f(x)在(?∞,1)單調(diào)遞減,又x2＞1,則2?x2＜1,又x1＜1,所以x1＜2?x2,即x1+x2＜2,得證.

典例2(河北省衡水中學2020 屆高三年級下學期三調(diào)第21 題)已知函數(shù)f(x)=xlnx ?+(m ?1)x+m有兩個極值點x1,x2,且x1＜x2.

(Ⅰ)求實數(shù)m的取值范圍;

(Ⅱ)若t≥1,證明x1+tx2＞t+1.

審題點撥本題的第(Ⅱ) 小題初看并不是嚴格的“x1+x2”形式, 但跟兩個零點之和相關, 只是多了一個參數(shù)t≥1,審題時要注意消參減元,可利用t和x2的范圍對式子進行放縮,從而達到消參減元的目的,這是解題的關鍵.最終化為x1+x2＞2,用策略一構造函數(shù)就能順利解決.

解題觀摩(Ⅰ)實數(shù)m的取值范圍為(1,+∞).(過程從略)

(Ⅱ) 證明: 由(Ⅰ) 知x1∈(0,1), 所以lnx1＜0,x2∈(1,+∞),所以當t≥1 時,x1+tx2=x1+x2+(t ?1)x2＞x1+x2+t ?1, 所以要證x1+tx2＞ t+ 1, 只需證x1+x2+t ?1＞t+1,即x1+x2＞2.證明如下:

令φ(x) =g(x)?g(2?x), 0＜x ＜1.所以φ(x) =lnx?x+m?[ln(2?x)?(2?x)+m]=lnx?ln(2?x)?2x+2,?2=＞0,所以φ(x)在(0,1)上單調(diào)遞增,又φ(1)=0,所以φ(x)＜0.因為x1∈(0,1), 所以g(x1)?g(2?x1)＜0, 即g(x1)＜g(2?x1), 又g(x2) =g(x1), 所以g(x2)＜g(2?x1).因為x2＞1,x1∈(0,1), 所以2?x1＞1, 因為g(x)在區(qū)間(1,+∞)上單調(diào)遞減,所以x2＞2?x1,即x1+x2＞2.所以x1+tx2＞t+1 成立.

策略二 分離零點(極值點)

策略探究分離零點的主要目的就是減元,進而建立與所求解問題相關的函數(shù).主要是利用函數(shù)零點(極值點)乘積所滿足的條件進行消參減元.其解題要點如下:

(1)分離零點(極值點),根據(jù)兩個極值點之積的關系,化簡或轉(zhuǎn)化所求解問題,進行消參減元.

(2)構造函數(shù),根據(jù)分離零點(極值點)后的式子結(jié)構特征,構建相應的函數(shù).

(3) 求解問題, 利用導數(shù)研究所構造函數(shù)的單調(diào)性、極值、最值等,從而解決相關問題.

典例3已知函數(shù)f(x)=lnx ?ax(a ∈R).

(Ⅰ)求函數(shù)f(x)的單調(diào)區(qū)間;

(Ⅱ)當a= 1 時,方程f(x) =m(m ＜?2)有兩個相異實根x1,x2,且x1＜x2,求證:x12.

審題點撥本題第(Ⅱ)問要證明的方程根之間的不等式關系比較復雜,此類問題可通過不等式的等價變形,將兩個根分布在不等式兩側(cè),然后利用函數(shù)的單調(diào)性轉(zhuǎn)化為對應函數(shù)值之間的大小關系即可.顯然構造函數(shù)的關鍵仍然是消掉參數(shù),確定x2的范圍之后才能將x1與化歸到函數(shù)的同一個單調(diào)區(qū)間上,這也是此類問題的一個難點——精確定位.

解題觀摩(Ⅰ)當a≤0 時,f(x)在(0,+∞)上單調(diào)遞增;當a ＞0 時,f(x)在上單調(diào)遞增,在上單調(diào)遞減.(過程從略)

(Ⅱ)證明: 由題意及(Ⅰ)可知,方程f(x) =m(m ＜?2)的兩個相異實根x1,x2滿足lnx ?x ?m= 0, 且0＜x1＜1＜x2, 即lnx1?x1?m= lnx2?x2?m= 0.由題意, 可知lnx2?x2=m ＜ ?2＜ln 2?2, 又由(Ⅰ) 可 知,f(x) = lnx ?x在(1,+∞) 上單調(diào)遞減, 故x2＞2.令g(x) = lnx ?x ?m, 則g(x)?+3 lnx ?ln 2.令h(t) =?t++3 lnt ?ln 2,t ＞2,則h′(t) =當t ＞2 時,h′(t)＜0,h(t) 單調(diào)遞減, 所以h(t)＜h(2) = 2 ln 2?＜0, 所以g(x)＜因為x2＞2 且g(x1) =g(x2), 所以g(x2)?=g(x1)?＜0, 即g(x1)＜因為g(x)在(0,1)上單調(diào)遞增,所以x1＜故

典例3 變式已知函數(shù)f(x)=lnx ?ax(a ∈R)有兩個零點x1,x2,求證:x1x2＞e2.

審題點撥形如x1x2＞x20的不等式, 可構造函數(shù)F(x) =f(x)?本題要證的不等式是兩個零點積的形式, 可考慮分離零點(極值點), 將兩個零點(極值點)視為變量,構造相關函數(shù).判斷兩個零點的取值范圍是關鍵之處,確定其范圍之后才能將x1與化歸到函數(shù)的同一個單調(diào)區(qū)間上.這體現(xiàn)了對數(shù)學建模等核心素養(yǎng)的考查.(解答從略)

策略三 比(差)值換元

策略探究比(差)值換元的目的是消參、減元,就是根據(jù)已知條件首先建立極值點之間的關系,然后利用兩個極值點之比(差)作為變量,從而實現(xiàn)消參、減元的目的.設法用比值或差值(一般用t表示)表示兩個極值點,繼而將所求解問題轉(zhuǎn)化為關于t的函數(shù)問題求解.

典例4(2019年金太陽高二期末聯(lián)考(理)第21 題)已知f(x)=xlnx ??x,m ∈R.若f(x)有兩個極值點x1,x2,且x1＜x2.求證:x1x2＞e2(e 為自然對數(shù)的底數(shù)).

審題點撥求解本題的關鍵點有兩個: 一是消參,把極值點轉(zhuǎn)化為導函數(shù)零點之后,需要利用兩個變量把參數(shù)表示出來,這是解決問題的基礎,若只用一個極值點表示參數(shù),如得到m=之后,代入第二個方程,則無法建立兩個極值點的關系,本題中利用兩個方程相加(減)之后再消參,巧妙地把兩個極值點與參數(shù)之間的關系建立起來;二是減元,即減少變量的個數(shù),只有把方程轉(zhuǎn)化為一個“變量”的式子后,才能建立與之相應的函數(shù),轉(zhuǎn)化為函數(shù)問題求解.本題利用參數(shù)m的值相等建立方程,進而利用對數(shù)運算的性質(zhì),將方程轉(zhuǎn)化為關于的方程,通過建立函數(shù)模型求解該問題,這體現(xiàn)了對數(shù)學建模等核心素養(yǎng)的考查.

解題觀摩欲證x1x2＞e2,只需證lnx1+lnx2＞2.由函數(shù)f(x) 有兩個極值點x1,x2, 可得函數(shù)f′(x) 有兩個零點, 又f′(x) = lnx ?mx, 所以x1,x2是方程f′(x) = 0 兩個不同實根.于是有

兩式相加, 可得lnx1+lnx2=m(x1+x2), 即m=兩式相減,可得lnx2?lnx1=m(x2?x1),即m=從而可得于是lnx1+lnx2=

由0＜ x1＜ x2, 設t=則t ＞1.因此lnx1+lnx2=,t ＞1.要證lnx1+lnx2＞2,即證＞2,即證當t ＞1 時,有l(wèi)nt ＞令h(t)=lnt ?則＞0, 所以h(t) 在(1,+∞) 上單調(diào)遞增.因此h(t)＞h(1) = 0.于是當t ＞1 時, 有l(wèi)nt ＞所以有l(wèi)nx1+lnx2＞2 成立,即x1x2＞e2.

典例5已知x1,x2是函數(shù)f(x)=ex ?ax的兩個零點,且x1＜x2.

(Ⅰ)求證:x1+x2＞2; (Ⅱ)求證:x1x2＜1.

審題點撥求解本題的關鍵點仍然是消參、減元,考慮到函數(shù)中含有ex,適合作差值換元,將要證明的式子作等價變換,變形出含有“x2?x1”的式子,從而換元,構造出一個新函數(shù),再判斷新函數(shù)的單調(diào)性,利用單調(diào)性證明不等式.

解題 觀摩(Ⅰ) 問題可以轉(zhuǎn)化 為y=g(x) =xe?x與y=有兩 個交點, 又g′(x) =易知g(x) 在(?∞,1)上單調(diào)遞增, 在(1,+∞)上單調(diào)遞減, 由x1＜x2,所以0＜ x1＜1＜ x2且

兩式相加, 得a=兩式相減, 得a=所以故要證x1+x2＞2, 即證變形為令t=x2?x1＞0, 則只需證t(et+1)?2(et ?1)＞0.設g(t) =t(et+1)?2(et ?1),t ＞0,則g′(t) =tet ?et+1,g′′(t) =tet ＞0, 所以g′(t) 在(0,+∞) 上單 調(diào)遞增, 即g′(t)＞g′(0) = 0.所以g(t) 在(0,+∞) 上單調(diào)遞增, 即g(t)＞g(0)=0,所以x1+x2＞2.

(Ⅱ) 要證x1x2＜1, 即證＜1, 等價于ex1ex2＜也即等價于令t=x2?x1＞0,等價于等價于等價于?et+ 1＜0.令h(t) =?et+ 1, 則h′(t) =令φ(t)=1+則所以φ(t)在(0,+∞)上單調(diào)遞減,所以φ(t)＜φ(0) = 0,從而h′(t)＜0,h(t)在(0,+∞)上單調(diào)遞減,所以h(t)＜h(0)=0.所以x1x2＜1.

本題第(Ⅰ) 問是x1+x2的形式, 也可用“策略一對稱變換”解決, 但需先化為y=g(x) =xe?x與y=兩個函數(shù), 確定x1,x2的取值范圍, 再設y=g(x) 的軸對稱函數(shù)y=g(2?x), 從而構造函數(shù)h(x) =g(x)?g(2?x)來解決.第(Ⅱ) 問可用“策略二分離零點”, 即構造函數(shù)φ(x)=g(x)?來解決.讀者可自行完成.

探究感悟著名教育家波利亞(Polya)認為,中學數(shù)學教育的根本目的是“教會學生思考”[4].極值點偏移問題的本質(zhì)是函數(shù)值變化快慢的問題,是導數(shù)在函數(shù)研究中的具體應用.基于數(shù)學核心素養(yǎng)下學生審題能力提高的策略探究,讓考生有較好的思路和途徑解決問題.在教學中,教師可以從具體、計算量小的函數(shù)模型出發(fā),認真審題,找出問題的結(jié)構特征,采用相應的解題策略,引導學生理解掌握極值點偏移的解題策略與通法,方向就是消參減元.循序漸進地訓練學生分析問題,構造函數(shù),通過導數(shù)研究函數(shù)性質(zhì),解決實際問題.讓學生體會數(shù)學學習的成就感,激發(fā)學生學習數(shù)學的興趣,促進學生數(shù)學核心素養(yǎng)的提升.