隨機超曲面模型容積卡爾曼擴展目標跟蹤算法*
(蘭州理工大學電氣工程與信息工程學院 蘭州 730050)
1 引言
目標跟蹤是指基于噪聲傳感器量測連續確定動態目標狀態的過程。大多數目標跟蹤算法是基于點目標模型的,即目標在每個采樣周期內最多只生成一個量測值,這就導致對目標的狀態識別較為單一,僅能依據單一量測信息對目標的運動狀態進行識別。然而,隨著高分辨率傳感器在目標跟蹤領域的廣泛應用,每個目標在每個每個采樣周期將對應多個傳感器量測值,稱這樣的目標為擴展目標(Extended Target,ET)。近幾年來,擴展目標跟蹤(ET Tracking,ETT)[1~2]問題引起了學者們的極大關注。通過充分利用ET的多個量測信息可以對其進行更為深入的跟蹤識別,即在實時跟蹤目標運動狀態信息的同時對目標的擴展狀態信息也進行一定程度的識別。
眾所周知,目標的形狀(輪廓)信息是擴展目標最為典型也最為重要的特征之一。因此,實現對擴展目標形狀的精確估計是提高擴展目標識別的關鍵所在。而完成擴展目標形狀的準確建模是實現形狀精確估計的前提。近些年來,對擴展目標形狀估計的研究已經取得了一定的成果[3~5],提出了各種擴展目標跟蹤算法。這些算法中絕大多數是基于擴展目標的形狀參數化建模,而隨機矩陣模型(Random Matrix Model,RMM)[6~8]是其最為典型的參數化建模方法之一。RMM在利用橢圓近似參數化表示擴展目標形狀特征的基礎上,利用高斯逆Wishart分布來描述目標的擴展狀態密度。但是,僅僅利用橢圓近似描述擴展目標的形狀較為粗略,這就導致不能準確估計出擴展目標的局部復雜輪廓特征。而Baum提出擴展目標量測源的近似非參數隨機超曲面模型(Random Hypersurface Model,RHM)[9~12]較好地彌補了RMM的缺陷,RHM非參數模型的核心思想是利用星凸參數曲面估計擴展目標的形狀。具體而言,RHM是在利用徑向函數描述星凸形擴展目標形狀的基礎上,對徑向函數進行有限階的傅里葉級數展開,通過展開的系數完成擴展目標形狀參數化建模,再結合尺度因子縮放擴展目標的輪廓完成對其表面量測源的建模。在這種方式建模下,選取的傅里葉級數的階數越高也就意味著對擴展目標的形狀估計越精確。但是,這種建模方式下擴展目標量測源的方程具有較強的非線性。因此,本文利用Arasaratnam提出的具有高濾波精度和數值穩定性的容積卡爾曼濾波(Cubature Kalman Filter,CKF)[13~14]算法對擴展目標 RHM 的非線性偽量測方程的高斯加權積分進行近似,進而完成對不規則形狀擴展目標的跟蹤估計。
本文針對不規則形狀星凸形擴展目標的跟蹤問題。首先利用RHM對星凸形擴展目標的形狀進行建模。然后詳細推導了基于RHM的CKF擴展目標跟蹤算法。此外,文中分別利用均方根誤差和擬Jaccard距離[15]對擴展目標的運動參數估計和形狀估計進行評測。最后,通過構造多種具有不同形狀的星凸形擴展目標的跟蹤實驗驗證了本文跟蹤算法的有效性。
2 隨機超曲面模型星凸形擴展目標建模
本文研究的擴展目標類型為星凸形擴展目標,這種類型的目標輪廓可以完全通過徑向函數描述。首先,星凸形可以定義為:如果一個形狀參數向量為的擴展目標S(ek)中至少存在一個點,以至目標中其他點與連接的線段完全屬于該目標,則稱這樣的擴展目標為星凸形擴展目標,其中目標參數向量為。
下面是利用RHM對擴展目標的形狀建模過程:


3 RHM擴展目標容積卡爾曼濾波跟蹤算法
RHM擴展目標容積卡爾曼濾波跟蹤算法由預測步與量測更新步構成。首先,給出該算法的預測步,其預測步與傳統的高斯濾波算法的預測步一樣。
1)預測步
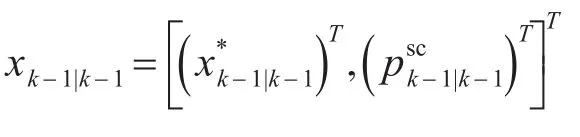

2)更新步
RHM擴展目標容積卡爾曼濾波跟蹤算法量測更新步的核心是結合k時刻擴展目標的所有量測信息以及基于RHM建立的擴展目標的量測源模型完成對擴展目標運動狀態和形狀的估計。具體流程如下。
首先,計算基本容積點ξi以及相應的權值wi,即

根據三階容積規則可知容積點總數nc為擴展目標狀態維數nx的2倍,即nc=2nx。完全對稱點集[1]可通過對單位向量e=[1,0,…,0]T的元素進行全排列和改變元素符號的方式得到,其中單位向量e的維數與nx相等,[1]i表示完全對稱點集[1]的第i個點。另外,由k時刻預測的擴展目標狀態向量xk|k-1和協方差矩陣Pk|k-1根據下式計算容積點,即

最后,計算增益矩陣并結合偽量測0更新擴展目標的狀態向量和協方差矩陣
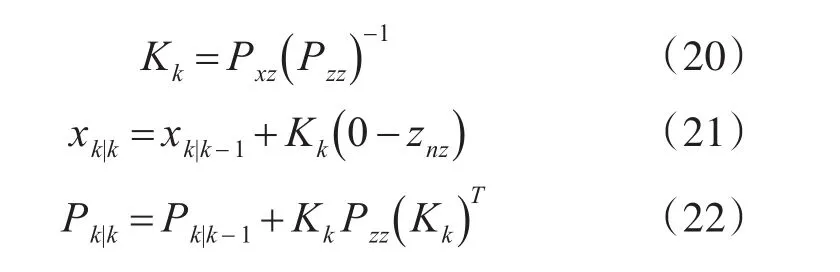
4 擴展目標狀態估計性能評價
不規則形狀星凸形擴展目標的狀態由運動狀態與形狀兩部分構成。為了全面評估文中所提算法對擴展目標的跟蹤性能。文中利用RMSE對目標質心位置估計進行評測,同時利用文獻[15]提出的擬Jaccard距離對擴展目標的形狀跟蹤性能進行評價。
擴展目標質心位置評測指標RMSE的定義為:如果k時刻的擴展目標真實位置向量為mk,利用本文跟蹤算法估計的位置為,那么RMSE的計算公式如下所示:

由擬Jaccard的計算公式可知,Jk的值越小,對擴展目標的形狀估計越精確。
5 仿真實驗
本文構造3種不同形狀且做CV運動(勻速直線運動)的星凸形擴展目標進行跟蹤仿真實驗。仿真場景設定擴展目標的運動區域為[0 , 1000] m×[0 ,1000] m,擴展目標隨時間的狀態演化服從線性高斯模型。采樣周期T=1s,采樣50個時刻,擴展目標的形狀參數的階數nf=11。過程噪聲標準差σw為0.03,量測噪聲是協方差矩陣為R=diag(0.32,0.32)的高斯白噪聲,尺度因子s~N( )2/3,1/18 。擴展目標在每個采樣周期內產生的量測數服從均值λ=50的泊松分布。
場景1:設置目標的形狀為十字架形,初始形狀是半徑為3的圓,初始狀態服從均值和方差分別為

的高斯分布。在上述仿真場景下,利用RHM擴展目標容積卡爾曼濾波跟蹤算法對擴展目標進行跟蹤,跟蹤結果如圖1所示。
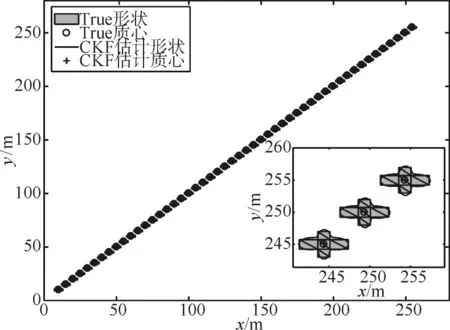
圖1 十字架形擴展目標的跟蹤效果圖
由圖1十字架形擴展目標的整體跟蹤效果以及形狀的局部放大圖可知,文中所提的RHM擴展目標容積卡爾曼濾波跟蹤算法能夠同時實現對十字架形擴展目標質心和形狀的精確估計。進一步,由圖2給出的RMSE與評測形狀估計效果的擬Jaccard距離的時間統計值看出,文中算法對十字架形擴展目標能夠進行準確的定位,與此同時,隨著量測信息的累積,對擴展目標的形狀也能實現準確的估計。
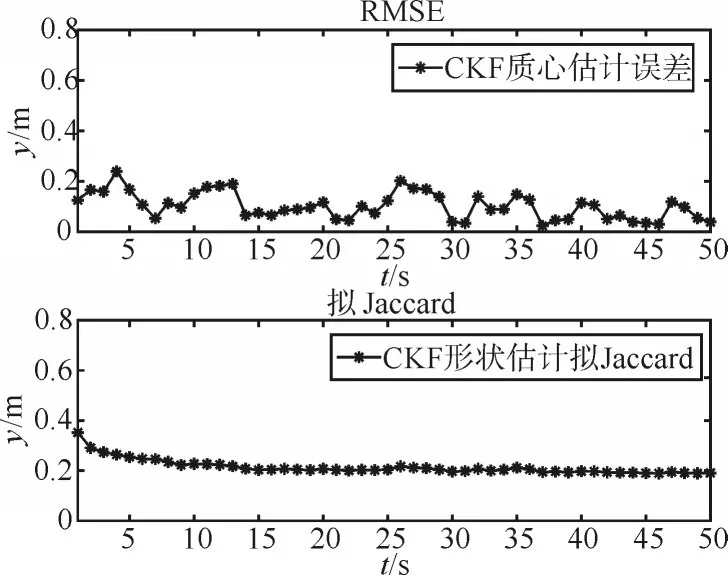
圖2 十字架形擴展目標RMSE與擬Jaccard距離
為了驗證文中所提出的RHM擴展目標容積卡爾曼濾波跟蹤算法的有效性和普適性,在上述仿真的基礎上,進一步設定場景2與場景3進行仿真實驗。
場景2:設定目標的真實形狀為做CV運動的五角星,初始形狀設置為半徑為6的圓形,其他參數與場景1相同。仿真結果如下所示。
由圖3和圖4五角星形擴展目標的跟蹤效果可得,當改變擴展目標的形狀時,RHM擴展目標容積卡爾曼濾波跟蹤算法也能夠依據擴展目標的量測信息對擴展目標的位置和形狀進行準確的估計。
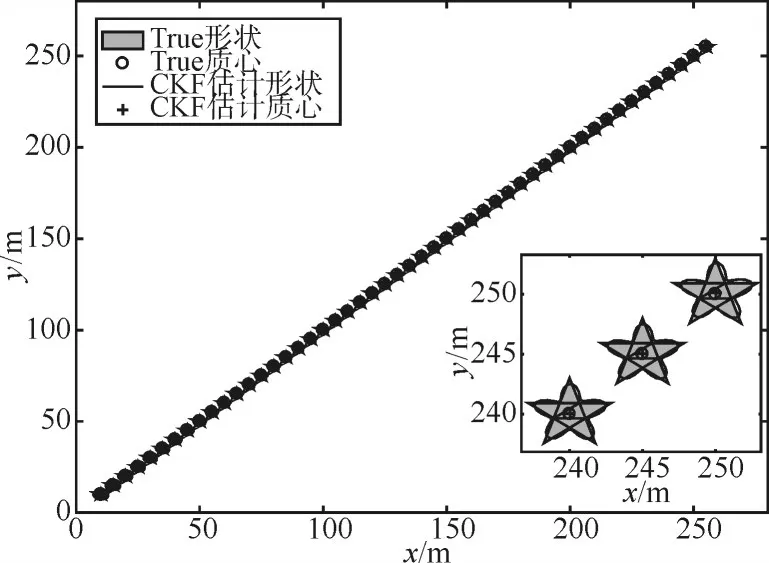
圖3 五角星形擴展目標的跟蹤效果圖
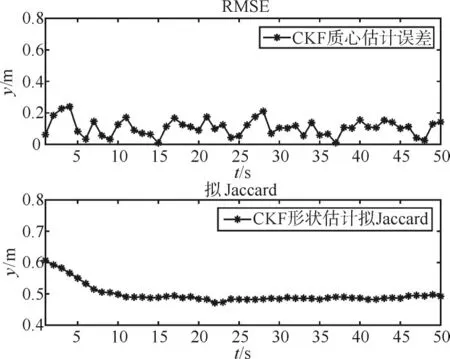
圖4 五角星形擴展目標RMSE與擬Jaccard距離
場景3:設定擴展目標的真實形狀為正方形,目標的初始形狀為半徑為4的圓形,同時改變目標的運動參數,即,其他參數與場景1和場景2相同。
由圖5與圖6正方形擴展目標的跟蹤效果圖可知,當改變擴展目標的運動速度和形狀時,并不能影響文中提出的RHM擴展目標容積卡爾曼濾波跟蹤算法的跟蹤性能。
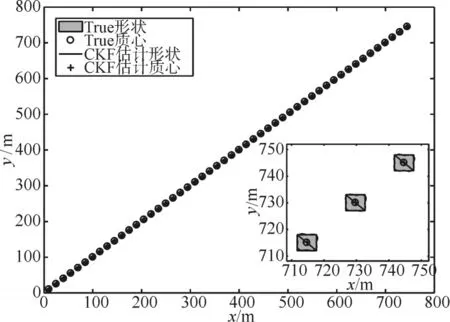
圖5 正方形擴展目標的跟蹤效果圖
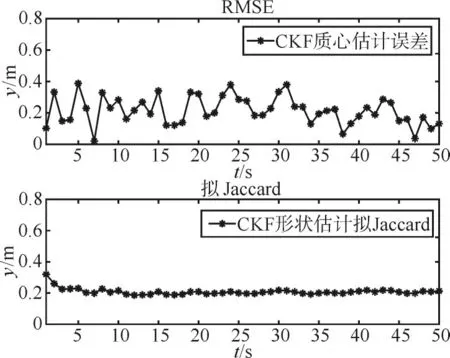
圖6 正方形擴展目標RMSE與擬Jaccard距離
6 結語
本文針對不規則形狀星凸形擴展目標的跟蹤問題,首先利用RHM對擴展目標的量測源進行建模,其次利用徑向函數對擴展目標的形狀進行參數化表示。然后詳細推導了基于RHM的容積卡爾曼擴展目標跟蹤算法。最后,構造多種形狀的星凸形擴展目標跟蹤仿真,驗證了本文所提算法的有效性。

