一類具有時滯的傳染病模型Hopf分支及穩定性分析

張露露,廖茂新,鄧興穎

(南華大學 數理學院,湖南 衡陽 421000)

0 引 言

傳染病是一類由病原體或寄生蟲引起的一類疾病，部分傳染病會長期伴隨人類共存，而有些傳染病會在有效的防治措施下逐漸消亡。[1]在人們與傳染病的長期抗爭過程中，研究者們逐漸發現，在人體受到感染后，感染初期并不會表現出任何的癥狀，在一定時間之后，某些癥狀才回逐步表現出來。[2-8]也就是說，在傳染病的傳播過程中，某時刻種群的變化除受當前狀態影響外，也會收到此前時刻的某些因素的影響[9]。但在研究初期，研究者們一般未考慮到時間滯后的因素。我們在傳染病模型中將時滯因素考慮進來，可以更加精準的反應傳染病的實際傳播機理及傳播形態，以幫助我們提出、制定更加有效的控制傳播范圍的措施[10-16]。

在前人的基礎上，本文研究了一類具有時滯和非線性傳染率的傳染病模型，研究了平衡點的穩定性，及Hopf分支的存在。在傳染病模型中引入時滯，用于模擬傳染病的潛伏期，利用基本再生數R0判斷疾病在一段時間時間發展后是仍然流行或是最終消亡；發現了在一定的條件下，時滯的引入會導致系統出現周期解，地方病平衡點E*處出現Hopf分支。

(1)

式中:S(t),I(t),R(t)分別表示在t時刻易感染人群、已感染人群和恢復人群的數量;k是比例常數，b為人口的新增率，d為人口的自然死亡率，u是已感染人群的自然恢復率，r是恢復人群失去免疫力后重新成為易感染人群的比率。

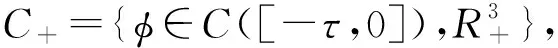
1 穩定性分析及Hopf分支存在的條件

(2)

對系統(1)首先分析其在平衡點E0處的穩定性。求得系統(1)的線性化矩陣為

(3)

特征矩陣為

(4)

定理1：當R0<1時，無病平衡點E0是局部漸近穩定的;當R0>1時，無病平衡點E0是不穩定的。

令f(λ)=0，得到λ1=-d,λ2=-(d+r)為特征方程的兩負根，且有λ3滿足

(5)

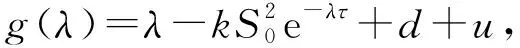
(6)

即

由于R0<1，則Re(λ)<0，則g(λ)=0的所有根具有負實部，則R0<1時，無病平衡點E0是局部漸進穩定的。

引理2：當R0>1，τ=0時，正平衡點局部漸進穩定。

證明：系統在正平衡點E*處的特征方程為

其中:p0=2d+r+u，p1=(d+u)(d+r)，p3=d+r，p4=d+r+u，a0=kS2(t)，b0=2kI(t)S(t)。

f1(λ)=0，易得λ=-d是方程負實根，其它根由以下方程確定

(7)

當τ=0時方程變為g1(λ)=λ2+p0λ+p1+(b0-a0)λ-a0p3+b0p4。

利用Routh-Hurwotz準則

p0+b0-a0=(2d+r+u)+2k×

則只需要b-dS*>0(R0>1)時，p0+b0-a0>0。

p1-a0p3+b0p4=(d+u)(d+r)+2k×

(d+r+u)

只需要b-dS*>0(R0>1)時，p1-a0p3+b0p4>0。

由Routh-Hurwotz準則知，方程根具有負實部，因此當τ=0,(R0>1)時，地方病平衡點E*局部漸進穩定。證畢。

引理3：當p1-a0p3+b0p4>0且p1+a0p3-b0p4<0時，方程具有一對純虛根±iθ(θ>0)。

證明：當τ>0時，g1(λ)=λ2+p0λ+p1+e-λτ[(b0-a0)λ-a0p3+b0p4]，將λ=iθ代入式中，并分離虛實部，得

(8)

兩式平方相加得(-θ2+p1)2+(-p0θ)2=(a0p3-b0p4)2+(a0θ-b0θ)2，化簡得

(9)

解得：

(10)

由式(8)，可得

(11)

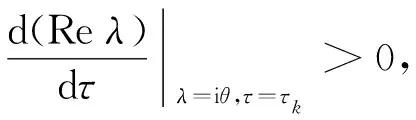
令

g1(λ)=λ2+p0λ+p1+e-λτ(q1λ+q2)

(12)

其中q1=b0-a0,q2=b0p4-a0p3。

式子(12)左右兩邊關于τ求導

(13)

可得

(14)

計算再有

(15)

則有

證畢。

由引理2、引理3、引理4，結合Hopf分支理論與文獻[4，11，16]可得到如下結論：

定理2：當p1-a0p3+b0p4>0，p1+a0p3-b0p4<0，且當R0>1時，如果τ∈[0,τ0)時，τ0=min(τj)，那么系統(1)的平衡點是局部漸進穩定;如果τ>τ0，那么系統(1)的平衡點是不穩定的，且當τ=τj時，系統(1)的平衡點經歷Hopf分支。

2 數值模擬

前文討論了時滯對無病平衡點及正平衡點的影響，接下來將通過數值模擬來直觀的展示出時滯對系統解的影響。取參數b=1，d=0.8，u=0.2，r=0.4，k=4，則系統(1)為

(16)

在同樣參數條件下，選擇τ=2.0>τ0時，此時地方病平衡點不再穩定(見圖2)。

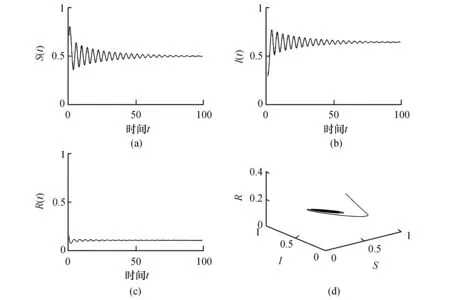
圖1 當τ=1.3<τ0時，模型(16)的正平衡解是漸進穩定的Fig.1 The positive equilibrium of (16) was asympomatic stable when τ=1.3<τ0

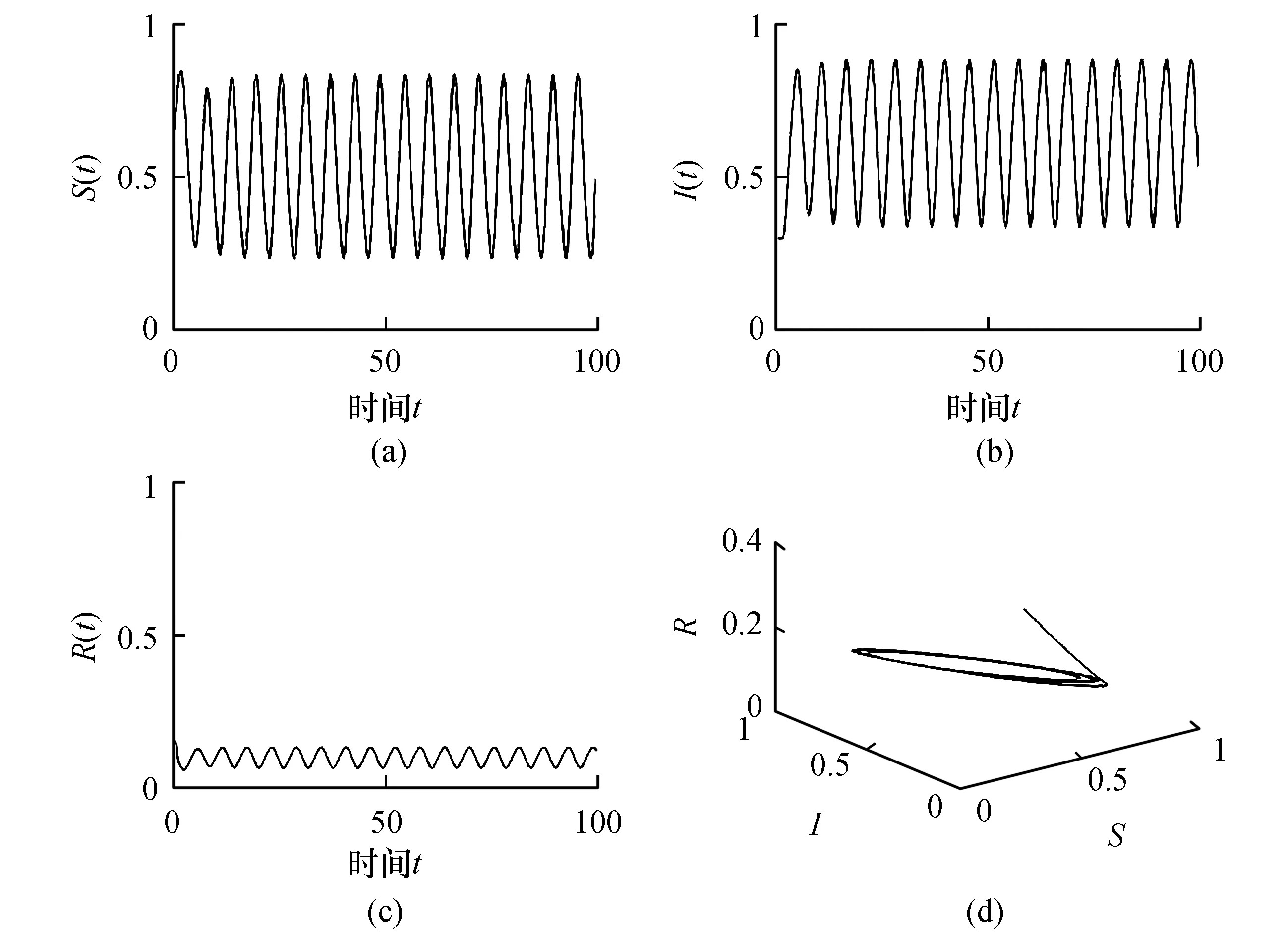
圖2 當τ=2.0>τ0時，模型(16)的正平衡解是不穩定的Fig.2 The positive equilibrium of (16) wasn’t stable when τ=2.0>τ0

3 結 論

本文討論了一個具有非線性發生率的具有時滯的流行病模型的穩定性，確定了基本再生數R0，由霍爾維茲定理判斷了非負平衡點的局部穩定性。對于任意時滯，當R0<1時，無病平衡點全局漸進穩定的，即隨著時間的推移，疾病最終消亡；R0>1，時滯不為零時，在一定條件下，E*不再穩定，系統出現周期解地方病平衡點出現Hopf分支。