基于仿生魚體結構的平板減阻方法

李廣浩, 馮 娜,2, 劉貴杰

基于仿生魚體結構的平板減阻方法

李廣浩1, 馮 娜1,2, 劉貴杰1

(1. 中國海洋大學 工程學院, 山東 青島, 266100; 2. 山東交通職業學院 航海系, 山東 濰坊, 261206)

海洋環境復雜, 流速變化幅度大, 一般的減阻方式在海洋中表現不穩定, 為更好地適應海洋環境, 文中提出一種新型減阻方法, 并通過數值仿真與試驗的方法驗證了減阻效果。首先根據仿生學原理, 選擇推進方式為靠身體/尾鰭游動模式的魚類作為研究對象, 仿照魚體重新建立模型。其次, 通過數值仿真的方法研究模型長度、高度和厚度對減阻效果的影響, 總結減阻規律并初步探究其減阻機理。通過流體試驗驗證了數值仿真的正確性。試驗結果表明, 隨著模型長度的增加, 其減阻效果會逐漸變差, 但產生最佳減阻效果時的流速并不受長度的影響; 模型高度的變化對整體減阻效果有很大影響; 隨著厚度的增加, 模型將在更大的流速范圍內出現減阻效果。重新建立的模型可以有效降低阻力, 并具有廣泛的流速適用范圍, 可以更好地適應海洋環境。

仿生魚; 減阻; 流體試驗

0 引言

能源問題一直制約著水下航行器的發展, 如何在水下有效節約能源受到越來越多人的關注。眾所周知, 不同流體因為黏性不同導致摩擦阻力有很大區別, 航行器在水中所受阻力約為空氣中的800倍。相關研究表明, 水下航行器運動時所受的粘滯阻力占總阻力的40%~80%[1], 水下航行器的大部分能源用于克服航行阻力。

為了更好地適應水下環境, 魚類進化出了多種獨特的結構。例如, 鯊魚具有特殊的盾鱗結構, 這種結構可以減小游動時所受的阻力[2-3]。Bechert等[4]通過模擬鯊魚皮膚的盾鱗結構得到了9.39%的減阻率。Zhang等[5]為闡述鯊魚盾鱗結構的減阻機理, 通過掃描電鏡(scanning electron microscope, SEM)技術研究發現盾鱗結構可以使流動更加穩定, 減小壁面粘滯阻力。海豚的柔性皮膚幫助海豚更快的游動[6-7]。英國生物學家Gary[8]發現, 當海豚以20 km/h的速度游動時, 理論上需要的能量約為食物攝入量的7倍, 這就是著名的Gary難題。Kramer[9]認為, 海豚的柔性皮膚可以抑制層流向湍流的轉捩, 進而實現減阻效果, 同時采用人造生物皮膚覆蓋的魚雷驗證減阻效果, 減阻率高達59％。Choi等[10]通過水洞試驗分析, 得出柔性皮膚的減阻效果可達5%并且對邊界層波動強度產生影響。除了上述特殊的減阻方法之外, 魚的外形在減小阻力方面也起到了至關重要的作用。

根據魚類推進特征可將魚類推進模式分為2類: 身體/尾鰭游動(body and/or caudal fin, BCF)推進以及間鰭和對鰭推進(median and/or paired fins, MPF)[11]。相關文獻表明, 85%的魚類運動模式為BCF模式[12]。BCF模式的魚類主要依靠魚體和尾鰭的流線型以及其柔性協同作用實現高效游動, 其中, 魚體的流線型外形可以有效降低阻力[13]。Barrett等[14]通過試驗的方式證明流線型外形的減阻效果, 發現: 牽引流線型魚狀物體所需的功率明顯小于以相同速度牽引筆直的物體所需功率。肖華攀等[15]探討了流線形狀的設計方法, 得出在二維層面上以半橢圓和拋物線構建的流線型阻力特性比較好。

目前存在的減阻方法主要依靠仿生生物皮膚, 如鯊魚、海豚等, 這些方法產生減阻效果的對應流速范圍相對較小, 無法適用復雜的海洋環境。為了解決這一問題, 文中基于魚體外形提出一種新的減阻方法, 該方法可應用到船舶側面、航行器表面等平坦壁面實現減阻效果, 擁有受環境影響小, 適用流速范圍大, 無需額外能量輸入的特點, 具有較高的工程價值。

1 基本理論

1.1 邊界層理論

液體流經物體表面時, 在物體表面產生一個薄層, 黏性力主要在薄層內產生, 即認為黏性作用完全局限在薄層內, 這個薄層被稱為邊界層。邊界層理論被廣泛用于解釋減阻機理, 邊界層構成如圖1所示。

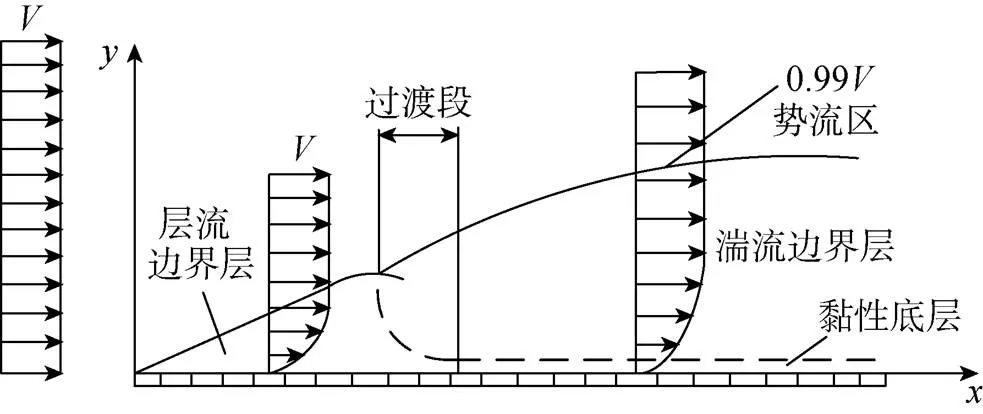
圖1 邊界層結構示意圖

1.2 研究思路及水下阻力構成

研究思路如圖2所示。

水下航行器在航行過程中所受阻力主要分為粘滯阻力和壓差阻力(形狀阻力)。

粘滯阻力是由于流體的粘度引起的。在靠近航行器的邊界層內, 流速由0很快增加到主流場流速, 這個過程中粘滯阻力起主要的限制作用。水下航行器在航行過程中, 原本的物理場受到干擾。航行器的前端壓力增加而后端壓力降低, 這種不對稱壓力引起的阻力稱為壓差阻力, 該阻力大小與形狀、迎流面積等因素有關。

2 試驗模型及參數

2.1 建立模型

以BCF模式的游魚作為仿生對象, 魚體模型如圖3(a)所示, 影響流線型的主要因素有長度、高度和厚度。對魚體進行重新建模, 如圖3(b)所示, 建模遵循半橢圓加拋物線原則[15]。其中為模型長度,為模型高度,為模型厚度(即魚體厚度, 圖中未標注)。

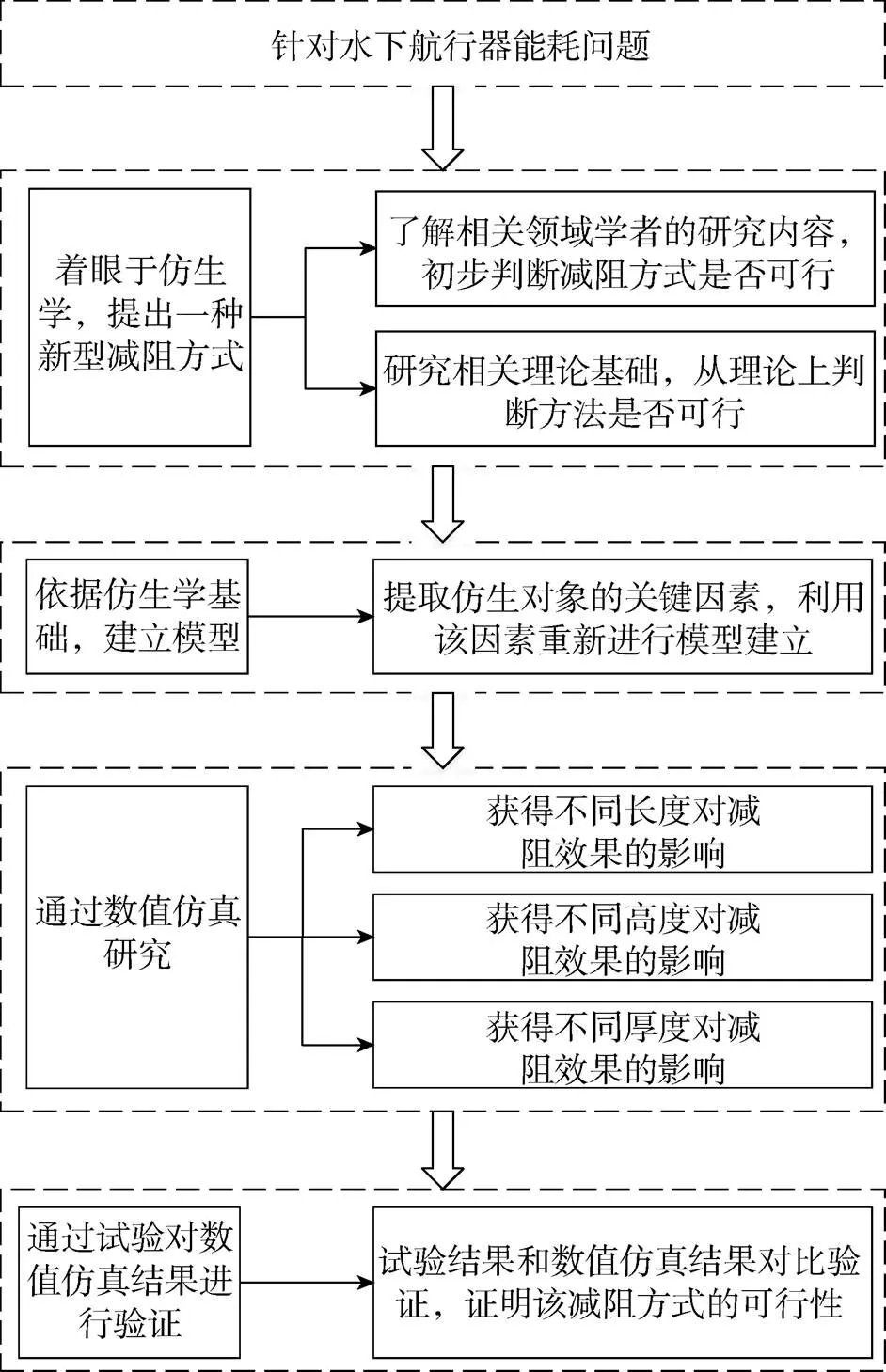
圖2 研究思路流程圖

圖3 魚體模型

2.2 模型參數設定

為探究不同長度、高度和厚度對減阻效果的影響, 依照控制變量試驗原則, 建立如表1所示8個模型, 相互作為對照組, 探究減阻規律。

3 數值仿真及結果分析

3.1 數值仿真模型建立

建立如圖4所示三維流域模型進行數值仿真, 其上表面為試驗面, 帶有試驗模型, 下表面為對照面, 未施加任何試驗模型。流場的長度為300 mm, 寬度和高度為150 mm。

表1 試驗模型參數

圖4 流域計算模型

利用流場分析預處理軟件ICEM對流域模型進行網格劃分。網格整體縮放比例為0.4, 網格數量為205 425 6, 第1層網格位于邊界層內。通過劃分不同數量的網格對比相對誤差來驗證網格無關性, 驗證結果如表2所示, 近壁面網格劃分如圖5所示。

表2 網格無關性檢驗結果

圖5 近壁面網格劃分示意圖

采用FLUENT軟件進行流場分析。流域入口設置為速度入口, 出口設置為自由流出口, 上下壁面設置為墻壁面, 無熱交換。文中內容主要面向海洋工況進行數值仿真, 以湍流的形式進行研究, 經過對數值模型的雷諾數計算, 最終選用-湍流模型[16], 近壁面函數選用標準壁面函數。

在流速相同的情況下, 上下壁面所受阻力的差值與對照面所受阻力的比值稱為減阻率, 即

3.2 模型長度對減阻效果的影響

為研究模型不同長度對減阻效果的影響, 選擇模型A, B和E作為研究對象。流場流速為1~ 10 m/s, 仿真結果如圖6所示。

圖6 流速為1~10 m/s時長度對減阻效果的影響

由圖6可知, 在流速相同的情況下, 模型長度越長, 減阻效果越差。隨著流速的增加, 3個模型的減阻效果均呈現下降的趨勢, 可以推斷最佳的減阻效果對應的流速在0~1 m/s范圍內, 對該范圍進行數值仿真, 結果如圖7所示。

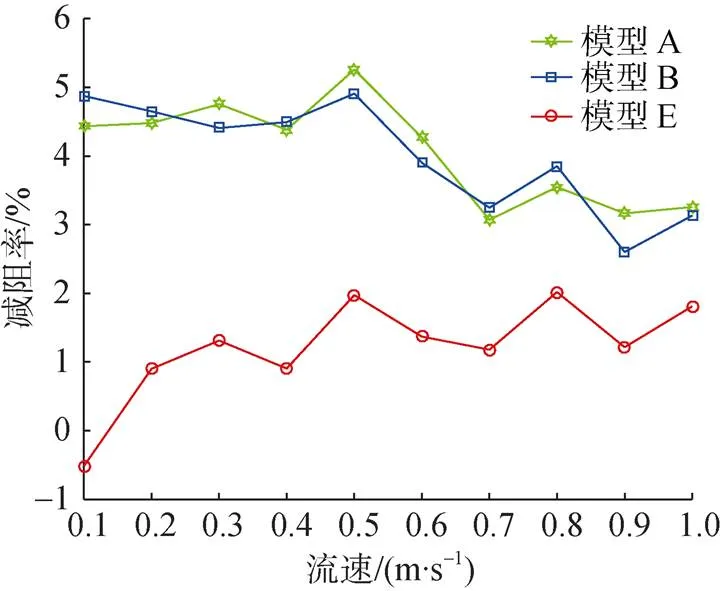
圖7 流速為0~1 m/s時長度對減阻效果的影響

由圖7可知, 3個試驗模型雖然長度不同, 但在速度為0.5 m/s時表現出最好的減阻效果, 最高減阻率為5.26%。可知, 長度會影響減阻效果, 但不會影響最佳減阻效果出現的流速。

3.3 模型高度對減阻效果的影響

為了獲得高度對減阻規律的影響, 選擇模型A、C和D作為研究對象。流場流速為1~10 m/s, 仿真結果如圖8所示。

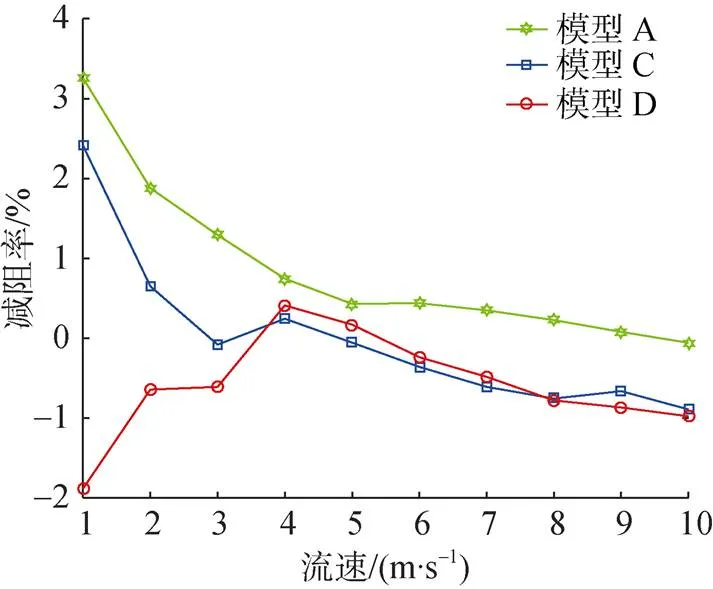
圖8 流速為1~10 m/s時高度對減阻效果的影響

由圖8可知, 模型A的減阻效果明顯優于其余2種模型, 且隨著流速的增大減阻效果呈現下降趨勢, 模型D雖然呈現先增大后減小的趨勢, 但整體不是在減阻反而是在增加阻力。模型A和C的最佳減阻效果應該出現在0~1 m/s處, 對0~1 m/s范圍內的數值仿真, 結果如圖9所示。

由圖9可知, 3個不同模型最佳減阻效果的匹配速度為0.5 m/s或0.6 m/s, 雖不完全相同, 但相差很小。高度會對最佳減阻效果的匹配速度造成影響, 但影響效果不大, 高度的不同更容易造成整體減阻效果的差異。

3.4 模型厚度對減阻效果的影響

為了研究模型厚度對減阻效果的影響, 選擇了模型D, F和G作為研究對象。流場流速為1~ 10 m/s, 數值仿真結果如圖10所示。

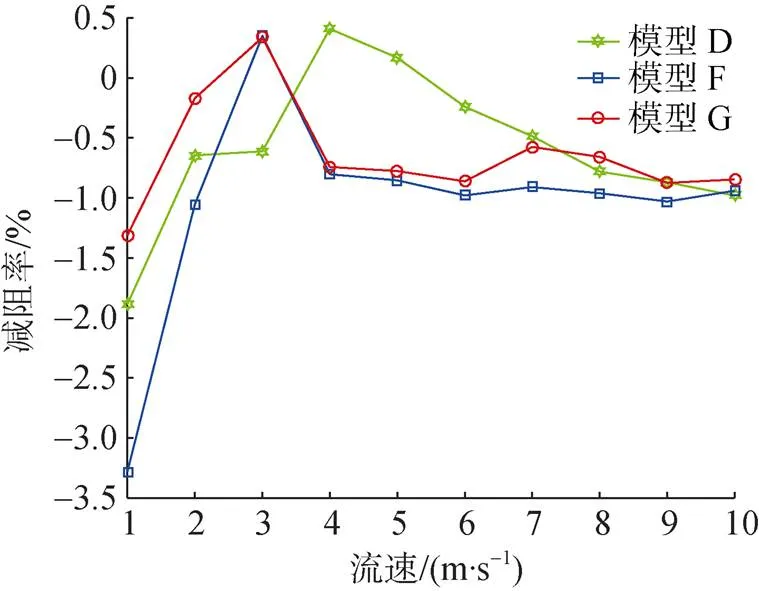
圖10 流速為1~10 m/s時厚度對減阻效果的影響

由圖10可知, 隨著流速的增加, 3個模型的減阻效果均呈現先增大后減小, 但值得注意的是, 以減阻率為0為界限, 模型F僅能在很小的速度區間內呈現減阻效果, 模型D在減阻效果上優于其余2個模型。可知, 隨著厚度的增加, 呈現減阻狀態的速度區間將不斷變大。

經過數值仿真分析可知, 無論哪種試驗模型, 當流速過高時, 均出現了減阻率小于0的情況。這是因為隨著流速的增加, 模型所受壓差阻力迅速上升, 壓差阻力的增加量遠大于粘滯阻力的減小量, 故總體減阻率小于0。

在實際應用過程中, 一旦減阻率小于0就意味著能量消耗更多而非節約能量。值得注意的是, 若選用合適的模型則可以一定程度上避免這種情況的發生, 如整體減阻效果較好的模型B在流速為0.1~9 m/s范圍內均呈現減阻效果, 即對于帶有模型B的航行器而言, 當航速低于32.4 km/h時均有減阻效果。這個適用范圍可滿足目前大部分水下航行器的作業需求。

3.5 減阻機理探究

試驗模型在水下所受阻力可分為壓差阻力(形狀阻力)和粘滯阻力。

壓差阻力主要受迎流面積和形狀的影響。形狀的變化將導致邊界層分離的變化, 從而產生壓差阻力。流線型模型與相同面積的正方形模型相比, 前者所受阻力僅為后者的1/25[17]。由不同形狀引起的壓差阻力如圖11所示。由此可見, 流線型可以獲得更小的壓差阻力, 有利于整體減阻現象的發生。

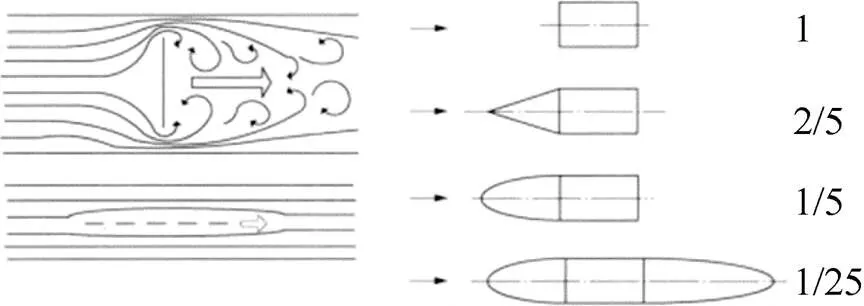
圖11 不同形狀壓差阻力的差異

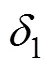
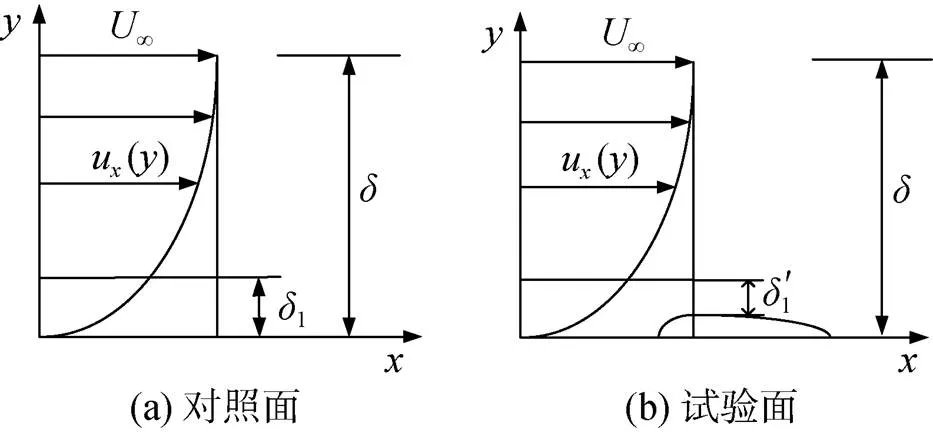
圖12 對照面及試驗面位移厚度

模型長度和高度的變化會影響減阻效果, 采用速度梯度圖進行解釋, 如圖13所示。

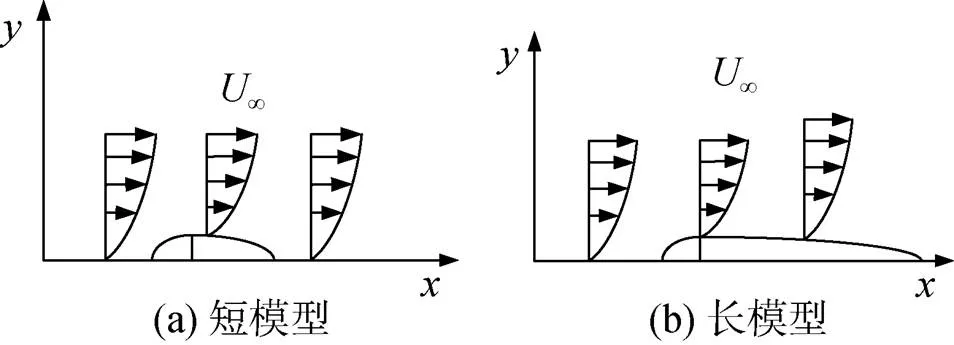
圖13 模型速度梯度圖

以試驗模型長度對減阻影響為例, 流體本身具有黏性, 當試驗模型自身長度比較短時, 對主流場的影響比較小, 此時邊界層并未有明顯改變, 如圖14所示, 其速度梯度如圖13(a)所示。當試驗模型的長度較長時, 在模型厚度會有明顯上升的速度梯度, 如圖13(b)所示, 此時邊界層發生改變, 不再產生減阻效果。

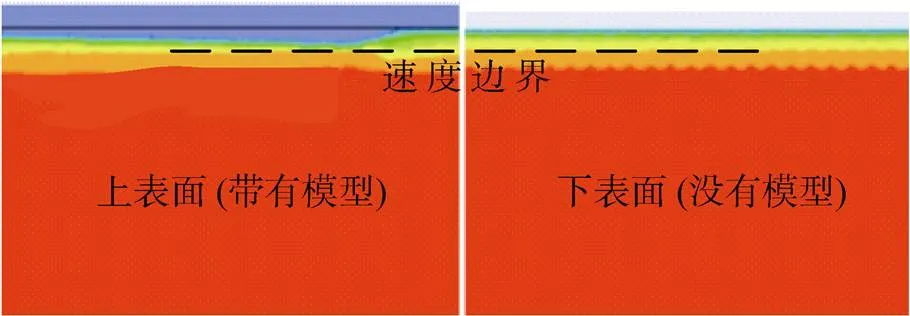
圖14 較短模型對流場速度的影響

綜上, 隨著模型長度的增加, 減阻效果逐漸變差。模型高度變化對減阻效果的影響機理與長度變化對減阻效果的影響機理相同, 在此不作贅述。

模型厚度的增加雖然能在一定程度上減小粘滯阻力, 但模型厚度越厚, 承受水流直接沖擊的面積越大, 對應的形狀阻力越大。粘滯阻力的減小量遠不及形狀阻力增加量, 所以增加模型厚度往往出現增加阻力的現象。

當流速較大時, 雖然模型本身為流線型, 但在模型的后部出現了脫落渦, 這些脫落渦使壓差阻力迅速增大, 自身減小的粘滯阻力遠不及增大的壓差阻力, 所以各模型在流速較高時, 均未表現出較好的減阻效果。

4 試驗結果及分析

4.1 試驗原理

為驗證數值仿真結果的正確性, 通過流體試驗進行對比驗證。

當流體流經平板表面時會發生能量損失, 這部分能量主要用于克服阻力做功。流經平面的阻力越大, 其損失的能量就越多。損失的能量在宏觀上表現為壓力差, 這部分數據可以通過壓力傳感器來收集, 即可以壓力來反應平板阻力的大小。

4.2 試驗裝置參數

試驗裝置如圖15(a)所示, 試驗裝置為矩形通道, 通道前后設置有壓力傳感器, 壓力傳感器數據經單片機傳至PC上位機, 可直接讀取壓力差數據, 試驗中采用的傳感器為MS5803-07BA壓力傳感器, 該傳感器具有精度高、分辨率高的優點, 最小分辨率可達4 Pa。傳感器自帶凝膠保護和防磁鋼帽, 滿足試驗的精度要求和防水要求。流場由水泵提供, 水泵共有100個擋位, 可用于控制流場流速, 試驗設備的具體參數見表3。試驗模型如圖15(b)所示, 具體數據見表1。

圖15 試驗裝置及其模型圖

表3 試驗裝置具體參數

試驗部分減阻率的數學表述為

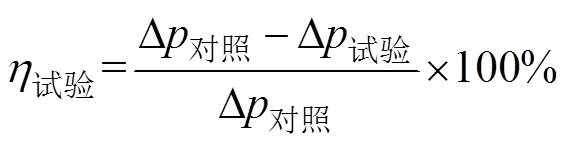
4.3 試驗結果分析

為研究模型長度對減阻效果的影響, 選用模型A、B和E進行試驗, 試驗結果如圖16所示。

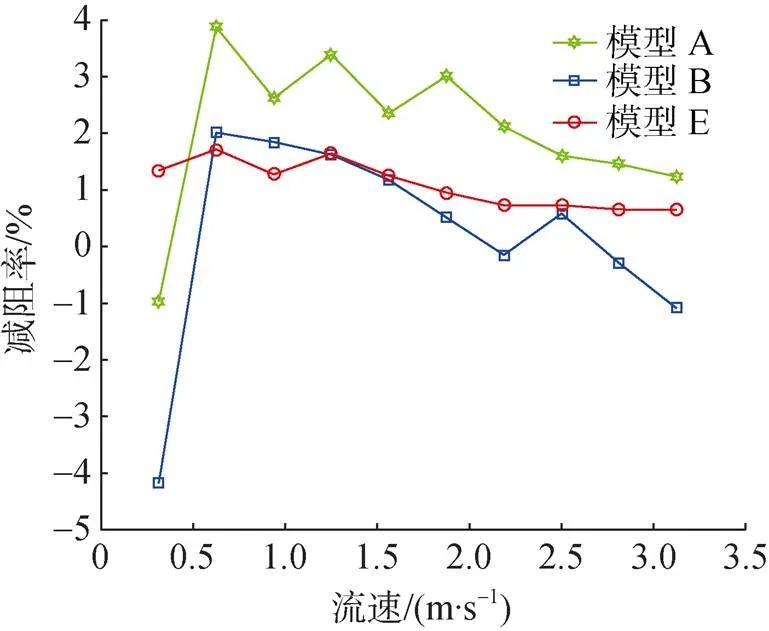
圖16 試驗中長度對減阻效果的影響

由圖可知, 當試驗矩形通道內的流速為0.625 m/s時, 3個模型的減阻效果最好, 試驗中的最佳流速與數值仿真中的最佳流速相近, 印證了數值仿真結果的可靠性。

模型長度的不同可以影響減阻效果, 但不會影響最佳減阻效果的匹配流速。

為研究模型高度對減阻效果的影響, 選用模型A、C和D進行試驗, 試驗結果如圖17所示。

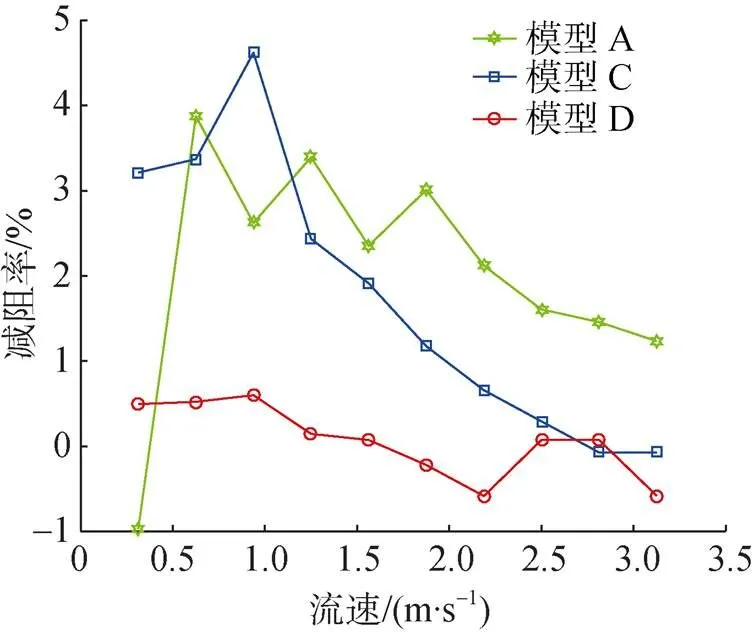
圖17 試驗中高度對減阻效果的影響

由圖17可知, 高度對減阻效果的影響規律和數值仿真所得規律相同。模型A和D表現出了較好的減阻效果, 并且最佳減阻效率的匹配流速相近。

為研究模型厚度對減阻效果的影響, 選用模型D、F和G進行試驗, 試驗結果如圖18所示。

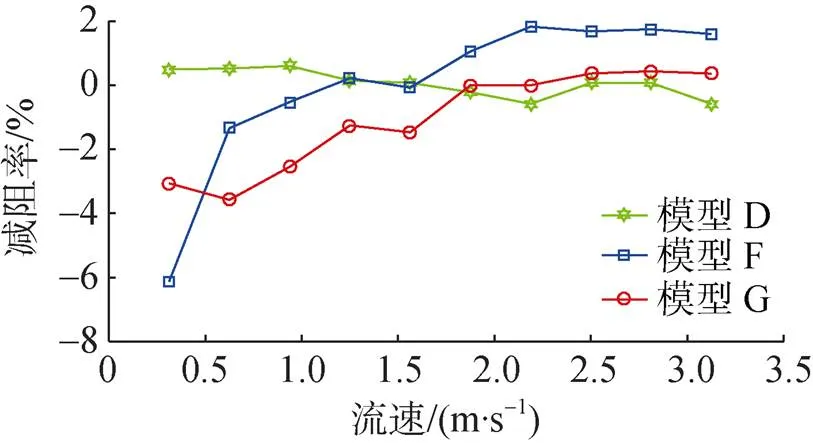
圖18 試驗中厚度對減阻效果的影響

在數值仿真結果中, 模型D、F、G在流速為3 m/s時才展現出減阻效果且模型D的減阻最差。由圖18可知, 當流速大于2.2 m/s時, 模型F的減阻效果最好, 模型G減阻效果次之, 這與數值仿真規律相同。

5 結論

基于仿生學原理提出一種適用于平坦壁面的新型減阻方法, 并通過數值仿真和流體試驗的方法進行分析, 得出以下結論:

1) 隨著模型長度的增加, 減阻效果逐漸變差, 減阻模型產生最佳減阻效果時的流速不受模型長度的影響;

2) 模型高度會明顯改變減阻效果, 隨著模型高度的增加, 模型減阻效果會先變差后逐漸變好, 對產生最佳減阻效果的匹配流速產生微弱影響;

3) 隨著模型厚度的增加, 模型產生減阻效果的流速范圍會出現明顯擴大。

文中方法可應用到船舶側面等平坦壁面, 不受環境影響, 不需要額外的能量輸入, 適用的流速范圍廣泛, 具有很高的工程潛力。

現階段等工作仍有些許不足, 建立的試驗模型體積較小, 在較大平面的使用時需要同時布置多個試驗模型才能達到良好的減阻效果。但如何排布才能實現最佳的減阻效果, 不同模型之間會不會相互影響, 這些問題都需在下一步工作中開展相應研究。自然界中, 魚類在遷徙過程中往往采用魚群的形式, 生物學家發現魚群結構有利于幫助魚類節約能量, 能否將這種特殊的生物活動形式借鑒到工程中, 解決較大平面的模型布置問題, 這也是未來研究的方向之一。

[1] 劉慶萍. 水—固界面系統二元仿生耦合減阻研究[D]. 吉林: 吉林大學, 2013.

[2] Lang A W, Motta P, Hidalgo P, et al. Bristled Shark Skin: a Microgeometry for Boundary Layer Control[J]. Bioinspiration & Biomimetics, 2008, 3(4): 046005.

[3] Walsh M J, Weinstein L M. Drag and Heat Transfer on Surfaces with Small Longitudinal Fins[C]//11th Fluid and Plasma Dynamics Conference. Seattle U. S. A.: AIAA, 2006.

[4] Bechert D W, Reif W E. On the Drag Reduction of the Shark Skin[C]//23rd Aerospace Sciences Meeting. Reno, U.S.A.: AIAA, 1985.

[5] Zhang D Y, Luo Y H, Xiang L I, et al. Numerical Simulation and Experimental Study of Drag Reducing Surface of a Real Shark Skin[J]. Journal of Hydrodynamics, 2011, 23(2): 204-211.

[6] Iurchenko N F, Babenko V V. Stabilization of Longitudinal Vortices by the Cutaneous Integument of Dolphins[J]. Biofizika, 1980, 25(2): 299-304.

[7] Kramer M O. Boundary Layer Stabilization by Distributed Damping[J]. Naval Engineers Journal, 2010, 72(1): 25-34.

[8] Gray J. Studies in Animal Locomotion[J]. Journal of Experimental Biology, 1933, 15(4): 506-517.

[9] Kramer M O. Boundary Layer Stabilization by Distributed Damping[J]. Naval Engineers Journal, 2010, 72(1): 25-34.

[10] Choi K S, Yang X, Clayton B R, et al. Turbulent Drag Reduction using Compliant Surfaces[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1997, 453(1965): 2229-2240.

[11] Wu Y T. Swimming of a Waving Plate[J]. Journal of Fluid Mechanics, 1961, 10(3): 321-344.

[12] 王碩, 譚明. 機器魚[M]. 第1版. 北京: 北京郵電大學出版社, 2006.

[13] Videler J J. Body Surface Adaptations to Boundary-Layer Dynamics[J]. Symposia of the Society for Experimental Biology, 1995, 49: 1-20.

[14] Barrett D S, Triantafyllou M S, Yue D K P, et al. Drag Reduction in Fish-Like Locomotion[J]. Journal of Fluid Mechanics, 1999, 392: 183-212.

[15] 肖華攀, 方子帆, 朱陳, 等. 水下流線型體的結構阻力特性及其應用研究[J]. 三峽大學學報(自然科學版), 2013, 35(6): 92-96.Xiao Hua-pan, Fang Zi-fan, Zhu Chen, et al. Structural Drag Characteristic and Application Research of Underwater Streamlined Body[J]. Journal of China Three Gorges University(Natural Sciences), 2013, 35(6): 92-96.

[16] Wilcox D C. Turbulence Modeling-an Overview[C]//39th Aerospace Sciences Meeting & Exhibit. Reno, U.S.A.: AIAA, 2013.

[17] 陳麗, 段登平. 大氣動/靜飛行器飛行原理[M]. 上海: 上海交通大學出版社, 2015.

1. 謝景鵬, 李宗剛, 杜亞江, 等. 基于視覺信息丟失的機器魚運動控制算法[J]. 水下無人系統學報, 2020, 28(5)

2. 朱紅秀, 杜闖, 褚彥斌, 等. 一種電磁驅動機器魚避障方法[J]. 水下無人系統學報, 2019, 27(6).

3. 胡橋, 劉鈺, 趙振軼, 等. 水下無人集群仿生人工側線探測技術研究進展[J]. 水下無人系統學報, 2019, 27(2).

4. 張晗, 王偉, 謝廣明. 面向水下機器人的水下電場通信協議設計[J]. 水下無人系統學報, 2019, 27(2).

5. 卞長生, 白萬發, 朱子才, 等. 基于IPMC仿生機器魚驅動技術研究[J]. 水下無人系統學報, 2019, 27(2).

6. 常龍飛, 李超群, 牛清正, 等. IPMC驅動柔性機器魚速度控制系統[J]. 水下無人系統學報, 2019, 27(2).

7. 劉鈺, 胡橋, 趙振軼, 等. 基于EMD與SVM的仿生機器魚人工側線智能探測方法[J]. 水下無人系統學報, 2019, 27(2).

8. 王延杰, 郝牧宇, 張霖, 等. 基于智能驅動材料的水下仿生機器人發展綜述[J]. 水下無人系統學報, 2019, 27(2).

9. 范增, 王揚威, 劉凱, 等. 仿生機器魚胸鰭波動與擺動融合推進機制建模及實驗研究[J]. 水下無人系統學報, 2019, 27(2).

10. 張守旭, 王寶峰, 嚴衛生. 基于事件驅動策略的多仿生機器魚編隊控制[J]. 水下無人系統學報, 2017, 25(4).

Flat Drag Reduction Method Based on Biomimetic Fish-body Structure

LI Guang-hao1, FENF Na1,2, LIU Gui-jie1

(1. College of Engineering, Ocean University of China, Qingdao 266100, China; 2. Navigation Department, Shandong Transport Vocational College, Weifang 261206, China)

Ocean environments are complex, wherein the variation in flow velocity is wide and the general drag reduction mode with robots is unstable. In this study, a new drag reduction method is proposed for robots to better adapt to ocean environments. The effect of drag reduction is verified by numerical simulations and experiments. First, based on the principle of bionics, a robot fish operating under a body and/or caudal fin(BCF) mode is selected as the research object, and the model is reconstructed to duplicate the fish body. Second, the effects of model length, height, and thickness on drag reduction are studied by numerical simulation. The law of drag reduction is also summarized, and the mechanism of drag reduction is investigatedintensively. The correctness of the numerical simulation is verified through a fluid experiment. Experimental results show that with an increase in the model length, the effect of drag reduction is gradually worsened. However, the flow velocity that preforms the best drag reduction effect is not affected by the length. The effect of drag reduction is greatly affected by the change in model height. With an increase in model thickness, the range of flow velocity that preforms drag reduction increases. The reconstructed model effectively reduces drag and has a wide range of flow velocity applications, thus enabling better adaptation to ocean environments.

biomimetic fish; drag reduction; hydrodynamic experiment

TB17; O351.2

A

2096-3920(2021)01-0080-08

10.11993/j.issn.2096-3920.2021.01.012

李廣浩, 馮娜, 劉貴杰. 基于仿生魚體結構的平板減阻方法[J]. 水下無人系統學報, 2021, 29(1): 80-87.

2020-02-25;

2020-05-14.

國家自然科學基金(61540010); 山東省自然科學基金(ZR201709240210).

李廣浩(1995-), 男, 在讀碩士, 主要研究方向為水下設備減阻.

(責任編輯: 許 妍)