基于有限元分析的三維齒輪接觸靜力學分析

林支慨，李瑞閣，燕 楠

(1.上海理工大學機械工程學院，上海200093； 2.上海理工大學光電信息與計算機工程學院，上海200093)

0 引言

接觸情況在機械工程中是廣泛存在的，尤其是在運動部件中，如軸承滾動體與內外圈的接觸、軌道車輛與鋼軌間的接觸、輪胎與地面的接觸。其中齒輪接觸是接觸情況中典型的問題，同時對于很多學者來說也是一大難點。許多學者為了解決一些齒輪問題花費了很多時間去研究，并且取得了一些成果。付昆昆等[1]用石川法和改進石川法來計算齒輪多齒時變嚙合的剛度數值，并與有限元法進行了對比，結果表明，改進石川法更能反映真實情況，結果更加精確。MAO K[2]使用微幾何修正法降低了齒面疲勞磨損程度，使得有限元計算的接觸應力更加精確。李學志等[3]為了解決斜齒輪在嚙合更替過程中受到載荷突變造成齒面點蝕和沖擊的問題，對斜齒輪接觸問題和修形問題進行了分析研究。卓耀彬等[4]為了使準雙曲面齒輪傳動系統更適合靜態齒面接觸分析，運用自己的方法重新建立了準雙曲面齒輪傳動系統的有限元模型。黃學文[5]為了能夠精確地得出斜齒輪副接觸時的狀態和應力大小的一般規律，用B樣條曲面在ANSYS中建立了精確的斜齒輪接觸齒面實體模型，并用有限元法對模型進行了接觸分析。

齒輪在實際應用中失效的主要形式是齒面損壞，所以在齒輪設計過程中對齒輪進行精確地分析是很重要的一個階段。這些接觸問題不僅關系到所設計出的產品壽命及功能是否滿足需求，甚至有可能會危及生命財產安全[6-7]。隨著科技的發展，齒輪的精度要求也更加嚴格。除了像設計方面的內在因素外，外在因素也是影響齒輪品質的重要原因，如齒輪熱脹時嚙合會產生幾何干涉，而長時間在熱脹區工作時會造成齒面膠合失效等問題，這些會直接導致齒輪失效，進而造成事故。目前，國內在接觸強度理論和彎曲理論方面的研究也有很多，如李廣興[8]為了解決某種汽車變速器二擋時齒輪副發出噪聲的問題，進行了噪聲分析仿真和一系列試驗研究。為了預測出齒輪和軸承的壽命，他們對齒輪激勵源和NVH問題進行了研究和分析，最后提出了新的修改方案，并解決了變速器噪聲問題。高準等[9]為了能夠精確計算齒輪在特定載荷下的變形情況，對基于Hertz接觸理論模型的行星傳動齒輪接觸問題進行了分析研究。

目前，有限元法是解決接觸分析問題中最常用的方法，在工程分析方面有限元法也是最經典的方法之一。它適用于多種領域，如彈塑性力學、熱傳導、流體力學等領域。雖然有限元的概念早就被學者們提出，但是由于當時計算機還沒有能夠被人們應用，有限元法也就沒有得到人們的重視。所以有限元的應用是離不開計算機發展的，因為計算機的不斷發展和應用使得有限元法在工程領域的應用成為可能，也只有在計算機的基礎上才會體現出有限元法的優勢。有限元的核心思想是結構離散化，是將復雜的模型用有限個相同規則的單元進行表示，目前應用的單元只有四邊形單元和六邊形單元。對于非結構化有限元網格來說，四邊形和六邊形有限元網格由于在計算精度、劃分網格數量等方面具有許多優勢，已經成為有限元分析中首選網格[8]。

很多文獻對于接觸分析其實并不是很精確，完全屬于理想狀態，并沒有考慮一些因素對模型接觸分析的影響，導致分析的結果不精確。本文在常規有限元分析的基礎上考慮表面切向應力對接觸應力分布的影響，結果表明，表面切向應力不僅影響模型的接觸應力分布，還會影響最大接觸應力值。本文還比較了四邊形與六邊形有限元網格在分析時的效率問題，在相同的網格單元大小的前提下比較接觸應力的收斂速度。結果表明，在相同大小的網格單元條件下，四邊形網格的收斂速度要比六邊形快，說明四邊形網格的分析效率相對更高效一些。這些都為以后的分析工作提供了參考價值，提高了分析模型的精確性和效率。

1 有限元接觸理論

彈性接觸問題最早是由赫茲提出并進行研究的，他提出了經典的赫茲接觸理論，但是該理論具有一定的局限性，在工程實際應用中只能對形狀簡單、接觸面相對簡單規整的問題進行分析和計算。因為這些條件的限制，赫茲理論主要被應用在齒輪接觸分析、軸承滾動體接觸分析、軌道車輛與鋼軌的接觸分析等領域。接觸理論包括Hertz解析算法和數值解法。

赫茲問題的解析解可通過赫茲公式計算得到。根據經典赫茲理論，兩個圓柱的最大接觸應力的理論公式為

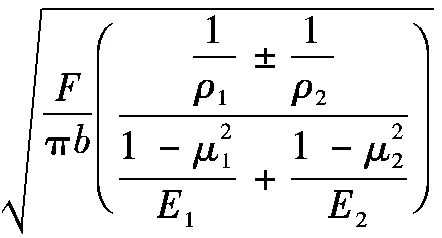
(1)

式中E1、E2——彈性模量

μ1、μ2——泊松比

b——厚度

ρ1、ρ2——半徑

F——外力

接觸面半寬

(2)

許用接觸應力

(3)

式中σHlim——齒輪的接觸疲勞極限

SH——齒面接觸疲勞安全系數

Von Mises應力是基于剪切應變能的等效應力。它用等值線來表示模型內部的應力分布情況，這樣可以清晰地表達出分析結果在整個模型中的變化，從而可以知道模型中最需要優化和改進的地方。求范式應力的理論公式為

σeq=

(4)

式中σ1，σ2，σ3——第一、二、三主應力

由彈性理論可以得到體積力與內力的關系方程

(5)

表面力與體內的應力存在的邊界條件

(6)

式中FSx、FSy、FSz——表面力在x、y、z方向的分量

l、m、n——表面外法線方向的余弦

2 有限元接觸分析

2.1表面切向應力對接觸分析的影響

當接觸變形條件和載荷條件確定時，都只會考慮表面的法向集中載荷，而忽略表面切向應力的影響。為了能夠更加精確地分析出接觸應力的分布，并且考慮零件表面疲勞的耐久性，本文考慮了表面切向應力。在有些應用中是可以不考慮表面切向力影響的，特別是在滾動軸承的應用，因為有充分的潤滑，所以在運動過程中都會忽略它們之間的滑動。這就表明，切向應力與法向應力相比是非常小的，所以切向應力在這種情況是可以忽略的。

有些情況是不能忽略的，如在測某零件表面疲勞的耐久性時，表面切應力就不能被忽略。因為表面切應力對于特定情況下的零件表面耐久性的影響是很重要的，所用到的計算方法也是很復雜的。

在考慮表面切向應力的情況下，對于兩接觸物體在接觸部位的von Mises應力的位置與法向應力和表面切應力的比值是有很大關系的。從圖1中可以看出不同應力出現的深度，隨著表面切應力與法向應力比值的增加，最大von Mises應力更接近于接觸表面，當τ/σ=0.3時，最大von Mises應力會出現在接觸表面上[10]。

圖1 不同的表面切應力(τ/σ)和材料應力 (σVM/σ)隨深度的變化Fig.1 Variation of surface shear stresses(τ/σ)and material stress(σVM/σ)with depth

2.2有限元接觸分析實例

兩個相同的1/4圓柱接觸的受力分析如圖2所示。圓柱半徑0.5 mm，厚度8 mm。材料的彈性模量E=3.5×106MPa，泊松比μ=0.3。載荷位置為上半圓的上表面，大小為100 N。約束位置為下半圓的下表面。

圖2 1/4圓柱接觸Fig.2 Quarter-cylinder contact

對于六面體網格單元，單元大小為0.05 mm的1/4圓柱接觸分析結果如圖3～4所示，不同單元大小

圖3 六面體網格單元1/4圓柱接觸分析Fig.3 Contact analysis of a quarter cylinder for hexahedral mesh element

下的分析結果如表1所示。從分析結果可以看出，最大接觸應力在模型接觸表面上。

圖4 六面體網格單元接觸分析局部放大Fig.4 Local magnification of contact analysis for hexahedral mesh element

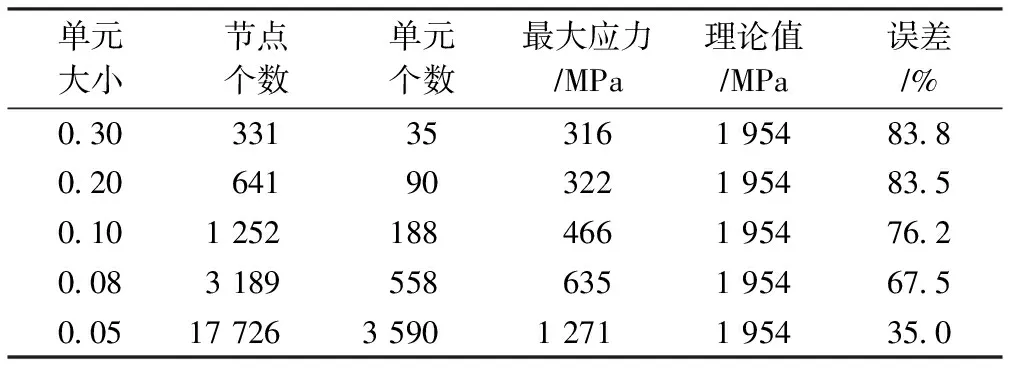
表1 六面體網格單元分析結果

對于四面體網格單元，單元大小為0.05 mm的1/4圓柱接觸分析結果如圖5～6所示，不同單元大小下的分析結果如表2所示。從分析結果可以看出，最大接觸應力的分布與六面體的有所不同，接觸表面和接觸次表層同時出現了最大接觸應力。

圖5 四面體網格單元1/4圓柱接觸分析Fig.5 Contact analysis of a quarter cylinder for tetrahedral mesh element

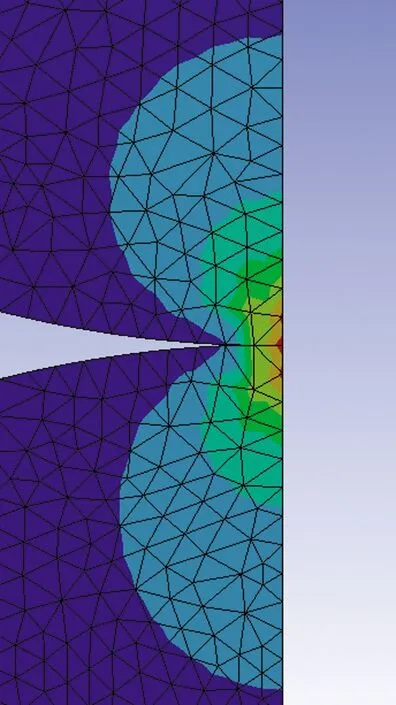
圖6 四面體網格單元接觸分析局部放大Fig.6 Local magnification of contact analysis for tetrahedral mesh element

表2 四面體網格單元分析結果

從表1～2中可以看出，在單元大小一樣的條件下，四面體單元分析的結果要比六面體單元的分析結果更精確，從收斂曲線(圖7)可以看出，四面體網格分析效率更高。為了使分析結果更加精確，可以使用局部畫網格的方法。在知道接觸應力最大值和位置情況下，可以對應力集中的地方進行局部細化，然后再進行分析，如圖8～10所示。

異戊烯醇聚氧乙烯醚(TPEG)：分子量1200；丙烯酸(AA)；醋酸乙烯酯(VAc)；馬來酸二乙酯(MADE)；丙烯酸羥丙酯(HPA)；烯丙基磺酸鈉(ALS)；過氧化二苯甲酰(BPO)、偶氮二異丁腈(AIBN)、過硫酸銨(APS)。

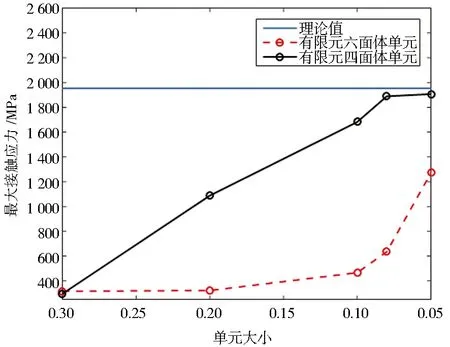
圖7 不同網格大小的最大接觸應力Fig.7 Maximum contact stress of different mesh sizes

圖8 四面體網格劃分模型Fig.8 Tetrahedral meshing model

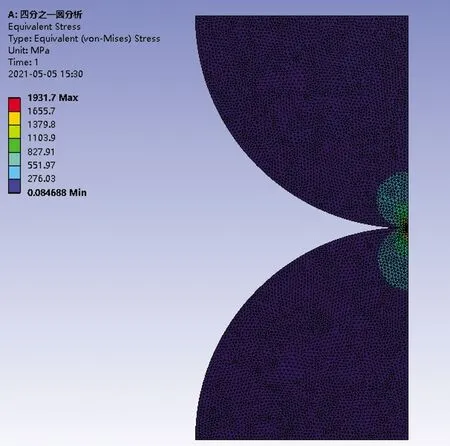
圖9 1/4圓柱接觸應力分布Fig.9 Contact stress distribution of a quarter cylinder

從分析結果可以看出，最大接觸應力出現在模型接觸表面的次表層，這是表面切應力對接觸應力的影響，最大接觸應力為1 931.7 MPa。根據赫茲理論的解析解公式可以計算得最大接觸應力為1 954 MPa，誤差為1.14%。

3 齒輪接觸有限元分析

在進行齒輪接觸分析時，需要考慮兩種嚙合狀態，第1種只考慮1對輪齒嚙合，第2種考慮多對齒嚙合，本文目前只考慮第1種情況。根據葛寶乾[11]計算推導出的公式可知，在不考慮齒輪彎曲變形，只考慮接觸變形時第1種情況接觸點的載荷為

圖10 有限元接觸分析局部放大Fig.10 Local amplification of finite element contact analysis

(7)

式中F——接觸點處的載荷

R1、R2——圓柱半徑

β——主動輪轉角

γ——公法線到齒輪回轉中心的距離

齒輪單齒嚙合最大接觸應力為

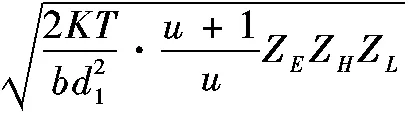
(8)

ZH——節點區域系數

ZL——重合度系數

K——載荷系數

T——轉矩

u——齒輪傳動比

d——分度圓直徑

b——齒輪厚度

設定齒輪模數m=2，齒數Z=40，壓力角為20°。上面的齒輪沿著軸心逆時針方向旋轉0.4°。材料的彈性模量E=2.1×105MPa，泊松比μ=0.3。

從圖11～12分析結果可以看出，最大接觸應力并沒有出現在齒輪接觸表面，而是出現在齒輪接觸表面的次表層，這說明在表面切向應力的作用下，接觸應力的分布發生了變化，且最大接觸應力為426.3 MPa。根據齒輪單齒嚙合最大接觸應力公式計算可得最大接觸應力為440 MPa，誤差為3.1%。

圖11 齒輪接觸有限元應力分布Fig.11 Gear contact finite element stress distribution

圖12 有限元齒輪接觸分析局部放大Fig.12 Local amplification of finite element gear contact analysis

4 結論

為了能夠更加精確、更加高效地得出齒輪接觸分析結果，考慮了表面切向應力對接觸分析的影響，考慮了四面體網格單元和六面體網格單元對分析效率的影響，并且用一個簡單實例驗證了這些因素的影響。從實例的分析結果可以看出：網格的類型會影響分析時的效率，四面體網格對模型分析的效率更高；表面切向應力對接觸模型也有影響，表面切向應力不僅影響接觸應力的大小，同時也改變了最大接觸應力的分布。在以上分析得出的結論基礎上，對直齒齒輪進行了有限元接觸分析，得到了三維齒輪的應力分布情況和最大接觸應力值，并計算出有限元分析結果與理論值之間的誤差。