淺談信號與系統課程中的譜概念
楊利軍 楊曉藝 趙晨萍


[摘 要]在信號與系統課程中,存在多個與譜有關的概念,例如頻譜分析、幅度譜、相位譜、能量譜和功率譜等,在教學過程中,這些概念常常讓學生感到疑惑,不清楚在什么情況下使用合適的概念去分析信號。針對該問題,項目組對信號與系統課程中出現的譜概念進行總結歸納,并給出相應的實驗分析,幫助學生理清這些與譜相關的概念之間的關系,為其學習起到一定的指導幫助作用。
[關鍵詞]信號與系統;頻譜分析;幅度譜;相位譜;能量譜;功率譜
[中圖分類號] G642 [文獻標識碼] A [文章編號] 2095-3437(2021)02-0115-03
信號與系統課程是電專業和非電專業(如通信與信息系統、自動控制、電子信息、信號與信息處理、計算機和生物醫學工程等學科專業)本科生必選的專業基礎課。該課程屬于理論和應用背景都比較強的專業基礎課。Fourier級數和Fourier變換是信號與系統課程中的重要學習內容,在信號分析領域占據著舉足輕重的地位。
一、Fourier級數和Fourier變換[1]
我們知道,對于周期為[T]的周期函數[f(t)],當它滿足狄里赫利(Dirichlet)條件時,可以展開成如下形式的Fourier級數:
絕對可積是函數Fourier變換存在的充分條件而非必要條件,引入廣義函數的概念后,許多不滿足絕對可積條件的函數也能進行Fourier變換。
所謂的頻譜分析,也稱為頻域分析,是指通過Fourier變換將信號變換到頻率域內對其進行分析,分析的工具是以頻率[ω]為自變量的各種物理量,幅度譜、相位譜、能量譜和功率譜就是這樣的物理量,對信號的頻譜分析其中就包含了對這些譜函數性質的研究。
二、幅度譜、相位譜、能量譜和功率譜
由上述(1)式可知,周期信號[f(t)]可分解為許多虛指數信號[ejnΩt]之和,其對應各分量的幅度為[Fn],而[Fn]為復數,因此可寫為
從而,幅值[Fn]、相位角[φn]均為[n]或([nΩ])的函數,分別稱為周期信號[f(t)]的幅度譜(也稱為振幅譜)和相位譜,其含義為幅度譜[Fn]刻畫了不同頻率分量(頻率[nΩ]隨[n]的變換而變化)的幅值隨頻率的變化情況,相位譜[φn]刻畫了不同頻率分量的初相隨頻率的變化情況。易知,[ Fn]為雙邊譜,且周期信號的幅度譜和相位譜均為離散函數。
由(3)式,非周期信號[f(t)]也可近似看作是分解為不同頻率的虛指數信號[ejωt]之和,與(1)式不同之處在于這里的頻率[ω]取連續值,稱[Fjω]為[ f(t)]的頻譜密度函數或頻譜函數,[Fjω]是一個復函數,可寫為
稱[|Fjω|]為非周期信號[f(t)]的幅度譜,[φω]稱為非周期函數[f(t)]的相位譜。由于這里的頻率[ω]取連續值,因此非周期信號的幅度譜和相位譜均為頻率的連續函數。
要理清能量譜和功率譜這兩個概念,需要先弄清楚能量信號和功率信號這兩個概念。根據教材[1],信號能量定義為在區間[(-∞,+∞)]中信號[f(t)]的能量,用字母[E]表示,即
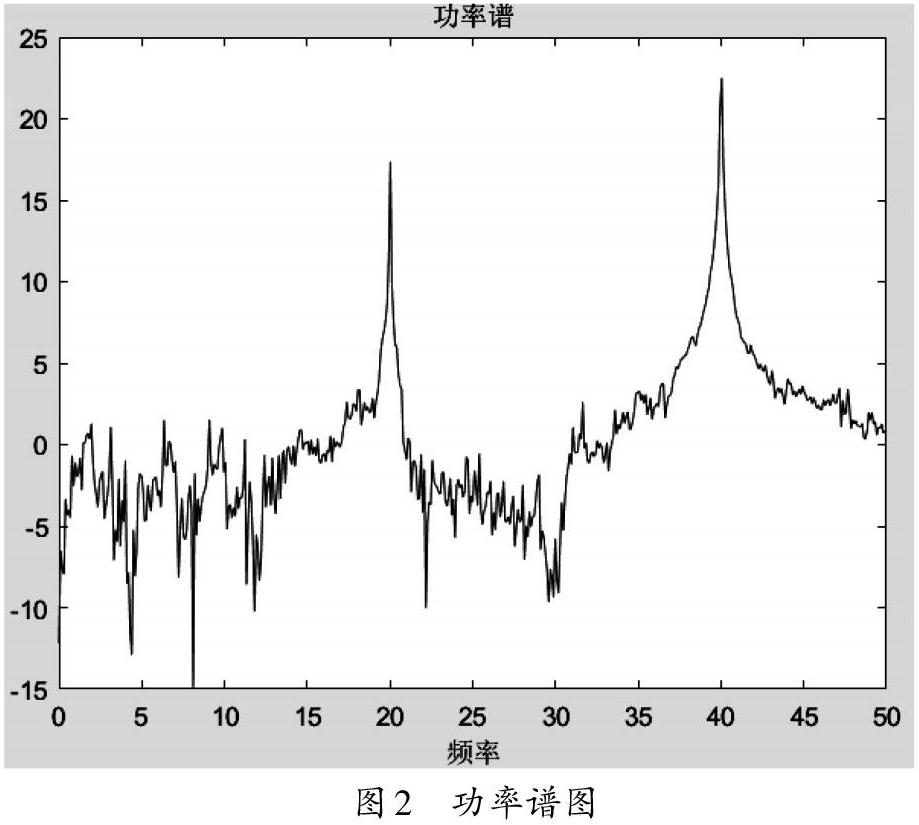
若對于信號[f(t)],其能量滿足[0 能量譜(也稱為能量譜密度)是針對能量信號而言的,是指用密度的概念表示信號能量在各頻率點的分布情況。能量信號[f(t)]的能量譜是該信號幅度譜的模的平方: 著名的Parseval定理(也稱為能量守恒定理)告訴我們,信號的時頻域能量相等,即如下式成立 從而對能量譜在頻域上積分就可以得到信號的能量。 功率譜(也稱為功率密度函數)是針對功率信號而言,是指用密度的概念表示信號功率在各頻率點的分布情況。由于功率為能量在所作用時間上的平均,因此功率譜在定義的時候需要借助截尾函數[fTt:] 則功率信號[f(t)]的功率譜密度定義為 其中[FT(jω)]為信號[fTt]的Fourier變換。功率譜的推導公式相對復雜,但根據維納-辛欽定理可知:信號的功率譜和信號的自相關函數是一個傅里葉變換對,因此可以通過自相關函數來求功率譜[2]。 對于非周期的確定性信號(為能量信號),常用能量譜來描述。而對于隨機信號(為功率信號),由于持續期時間無限長,不滿足絕對可積與能量可積的條件,因此不存在傅立葉變換,所以通常用功率譜來描述。周期性的信號,也同樣是不滿足傅里葉變換的條件,因而常用功率譜來描述。只有如單頻正弦信號等很少的特殊的信號,在引入[δ](delta)函數之后,才可以求解信號的傅里葉變換。 三、實驗分析 在本小節,我們基于MATLAB軟件給出相關譜概念的實例,從可視化的角度理解這些概念。由于能量譜是幅度譜的平方,因此,這里只給確定性信號的幅度譜和相位譜,以及隨機信號的功率譜的實驗結果。 實驗1 繪制信號[gt=0.5sin40πt+2sin (80πt)]的幅度譜。 在本例中,采樣頻率為[fs=100Hz]。圖1(a)給出了信號[g(t)]的頻率在[0~50Hz]范圍(奈奎斯特采樣頻率為[50Hz])的幅度譜圖,從圖中可以清晰識別到信號的兩種頻率成分:[20Hz]和[50Hz]。圖1(b)是對應的相位譜圖。 本實驗的MATLAB的代碼如下: 圖2中,雖然信號受到了隨機噪聲的干擾,信號[h(t)]的譜圖有很多毛刺,但從功率譜圖上還是可以清晰識別出信號的兩種頻率成分:20Hz和50Hz。本實驗利用了維納-辛欽定理來計算信號的功率譜。 本實驗的MATLAB代碼如下: 四、結論 本文針對信號與系統課程中學生易混淆的幾個與譜相關的概念進行總結歸納,并給出相應的MATLAB實驗可視化地理解這些概念,便于學生理清相關譜的概念以及各概念之間的關系,指導幫助學生的課程學習。 [ 參 考 文 獻 ] [1] 吳大正主編.信號與線性系統分析[M].第四版.北京:高等教育出版社,2005. [2] Alan V Oppenheim,Alan S Nillsky,S Hamid Nawab.信號與系統[M].第二版.劉樹堂,譯.北京:電子工業出版社,2013. [3] 鄭君里,谷源濤.試談“信號與系統”課程理論與實踐之結合[J].電氣電子教學學報,2014(3):1-5. [4] 王法松.“信號與系統”課程中關于信號相位譜的分析[J].微型電腦應用,2018(9):1-3. [5] 孫明.基于GUI的周期信號頻譜分析演示系統設計[J].實驗室科學與技術,2018(1):18-21. [責任編輯:黃緊德]

