基于BP神經網絡的旋風分離器分割粒徑模化與預測

劉金鵬，趙兵濤，錢魏鋒，李會梅

（1 上海理工大學能源與動力工程學院，上海200093；2 上海市動力工程多相流動與傳熱重點實驗室，上海200093）

旋風分離器作為常用的離心式氣固分離設備，廣泛應用于固體粉塵收集、循環流化床、石油催化裂化、氣溶膠采樣等工業場景中[1-3]，其一般結構如圖1所示。分割粒徑（定義為旋風分離器分級效率為50%時的顆粒空氣動力粒徑）是評估旋風分離器分離性能的重要參數，小的分割粒徑一般意味著高的分離性能[4]。

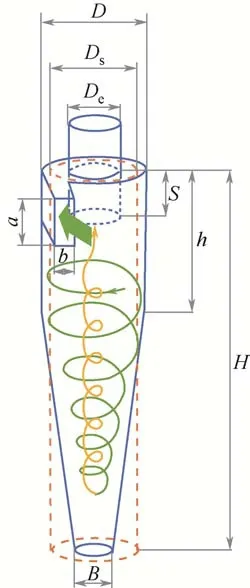
圖1 旋風分離器結構尺寸

為預測分割粒徑，基于多種模型和理論的表征方法在過去幾十年相繼被發展[5]。早期以理論模型[6-7]和半經驗模型[8]為主，停留時間理論和平衡軌道理論的應用對分割粒徑的表征有了詳盡的物理描述。但由于近似簡化和條件假設的建模方式，預測精度并不理想[9]。相較于對復雜機理的建模，基于數據驅動的多元回歸模型受到關注[5]，它們主要將表征分割粒徑大小的量綱為1 數Ψ0.5作為因變量，與操作參數[10]和部分尺寸參數[11]進行關聯，模型決定系數可以達到0.980 以上，但沒有考慮到其他重要尺寸參數的影響。Zhao等[9]模型間接關聯了旋風分離器廣義尺寸參數和操作參數，更全面地評估了分割粒徑的影響因素，模型決定系數為0.973，但其預測精度仍有進一步提高的必要性。

近年來，人工神經網絡憑借優越的非線性擬合能力在旋流分離領域得到重視[12]。如Safikhani 等[13]通過GMDH 型神經網絡得到了分割粒徑的預測模型，但只關聯了部分尺寸參數。Elsayed 等[14]運用RBF神經網絡對Stokes數預測，預測是基于訓練集而不是測試集的結果且網絡輸入缺少重要操作參數的響應。因此關聯全局的結構與操作參數、合理發展和選擇自變量，比較與評估神經網絡模型中的算法、參數及其優劣性，從而高精度模化旋風器的分離性能仍是當前面臨的科學技術問題之一。

本研究的目的是通過關聯旋風分離器全局尺寸參數和操作參數構建一個基于前饋性BP 神經網絡（BPNN）的分割粒徑預測模型，通過比較不同算法包括L-M算法[15]、擬牛頓算法[16]和貝葉斯正則化算法[17]以及隱含層神經元個數的組合預測性能對BPNN 模型進行優化，最后對BPNN 分割粒徑模型的預測性能進行評價，并與其他理論模型、半經驗模型和多元回歸模型進行比較。本文以期為不同結構旋風分離器性能參數的評估提供一種精確有效的方法。

1 BPNN分割粒徑模型模化過程

1.1 BP神經網絡基本原理

BP 神經網絡（back propagation neural network，BPNN）運用誤差反向傳播的方式修正權值、閾值[18]。由輸入層、隱含層和輸出層構成，隱含層神經元個數足夠時，三層結構的BP 神經網絡可以很好地逼近一個參數有限的不連續函數[19]。當有i 個輸入、j 個隱含層神經元和k 個輸出時，隱含層的輸出如式(1)所示。

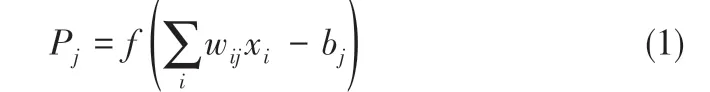
式中，wij為輸入層與隱含層的連接權值；xi為輸入變量；bj為隱含層閾值；f為隱含層激活函數。隱含層常用S型函數作為激活函數，主要分為logsigmoid 函數和tan-sigmoid 函數。雖然都存在著梯度消失的問題，但是相較于log-sigmoid函數，tansigmoid的輸出是以0為中心的，收斂速度快，同時在非線性預測領域中得到了成功的應用[20]，所以本文選用tan-sigmoid 函數作為隱含層的激活函數，其表達式如式(2)所示。

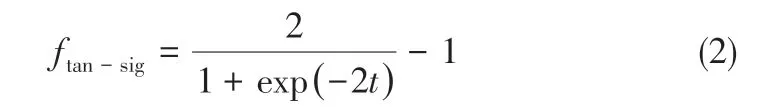
式中，t 為隱含層輸入變量。輸出層輸出如式(3)所示。

式中，wjk為隱含層與輸出層的連接權值；bk為輸出層閾值；g為輸出層傳遞函數，本文選用線性函數purelin 函數作為輸出層傳遞函數，其表達式如式(4)所示。

式中，a為輸出層輸入變量。

1.2 BP神經網絡模型變量參數

旋風分離器主要包含8 個結構尺寸參數，如圖1所示，分別是進口高度a、進口寬度b、排氣芯管直徑De、排氣芯管插入深度S、筒體高度h、總高度H、排塵口直徑B、筒體直徑D，它們的改變對分割粒徑有著不同程度的影響[21-25]。此外，Dring等[26]發現兩個量綱為1 參數比(ρg/ρp)r0/Dp、Re0Dp/r0可用于描述旋流中粒子的軌跡，其中ρg為氣體密度、ρp為顆粒密度、Dp為顆粒粒徑、r0為初始旋流半徑。從中可知顆粒粒徑的量綱為1比Dp/r0與旋流雷諾數Re0高度關聯，所以旋風分離器結構尺寸參數和操作參數對空氣動力等效分割粒徑dp0.5的綜合影響表征如式(5)所示。

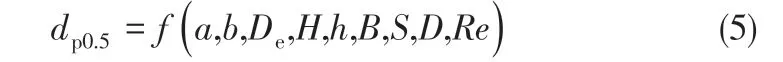
由于輸入參數過多會使BP 神經網絡模型的復雜度增加，所以需要降低數據維度來提高模型質量，另外對輸入、輸出參數的量綱為1處理可以進一步簡化模型。

如圖1 所示，在常見的筒錐結構旋風分離器中，筒段與錐段的直徑不同導致顆粒的分離距離不同，Zhao等[9]為了克服這種不均勻性，運用等效體積法構建出等效分離距離Ds，其間接地關聯了h、H、B、D 四個尺寸參數，運用Ds可以更綜合地表征旋風分離器本體尺寸參數對分割粒徑的影響，等效分離距離的量綱為1 幾何參數可以表征如式(6)所示。

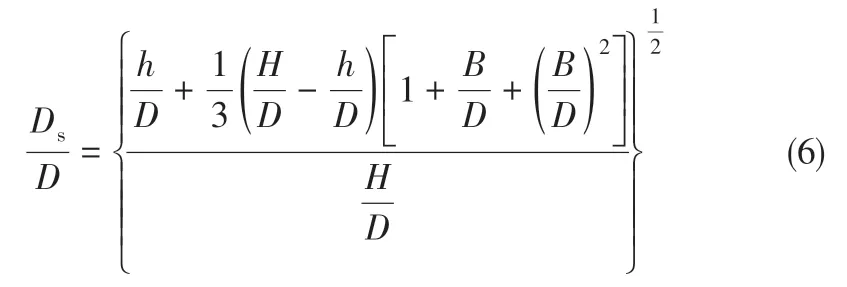
Moore等[10,27]的研究表明，流體流動特性對顆粒沉降的影響可以用氣體雷諾數Re 表征，但是環形空間雷諾數Reann被認為對表征空氣動力等效分割粒徑大小的量綱為1數Ψ0.5有著更好的關聯性，Reann、Ψ0.5計算分別如式(7)、式(8)所示。

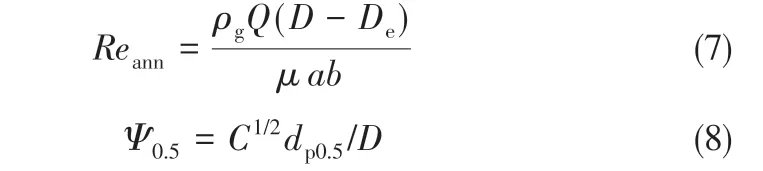
式中，Q為氣體流量；C為Cunningham修正系數；Reann中包含著對外部尺寸參數進口高度a、進口寬度b、排氣芯管直徑De的間接表征。同時Lidén 等[11]認為Ψ0.5除了與Reann有很好的關聯性外，S/D 對Ψ0.5也有著很大的影響。聯合式(5)～式(8)，Ψ0.5與旋風分離器結構尺寸參數和操作參數之間的聯系可以表征如式(9)所示。

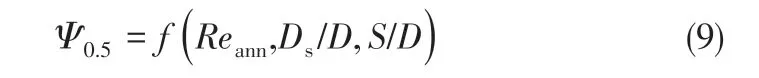
在神經網絡建模中，選用Reann、Ds/D、S/D 三個量綱為1數作為BP神經網絡的輸入參數、Ψ0.5作為輸出參數。

1.3 數據集劃分與網絡參數設置

本文使用156 組數據樣本的數據集[28-39,8,24]建立BP 神經網絡模型，表1 為數據集分布情況。通過分層抽樣法按數據源屬性劃分，將數據分為14份，再運用Kennard-Stone 算法[40]將每份數據按照85%∶15%的比率劃分為兩份，合并每份中85%的樣本作為訓練集，15%的樣本作為測試集。

在運用模型訓練和測試時，均將參數歸一化到[-1,1]區間內，最終模型輸出的值經過反歸一化轉換成實際數量級的值。網絡參數設置中迭代次數為1000次，目標精度為1×10-5，驗證集最大失敗次數為100次（貝葉斯正則化算法無此參數）。

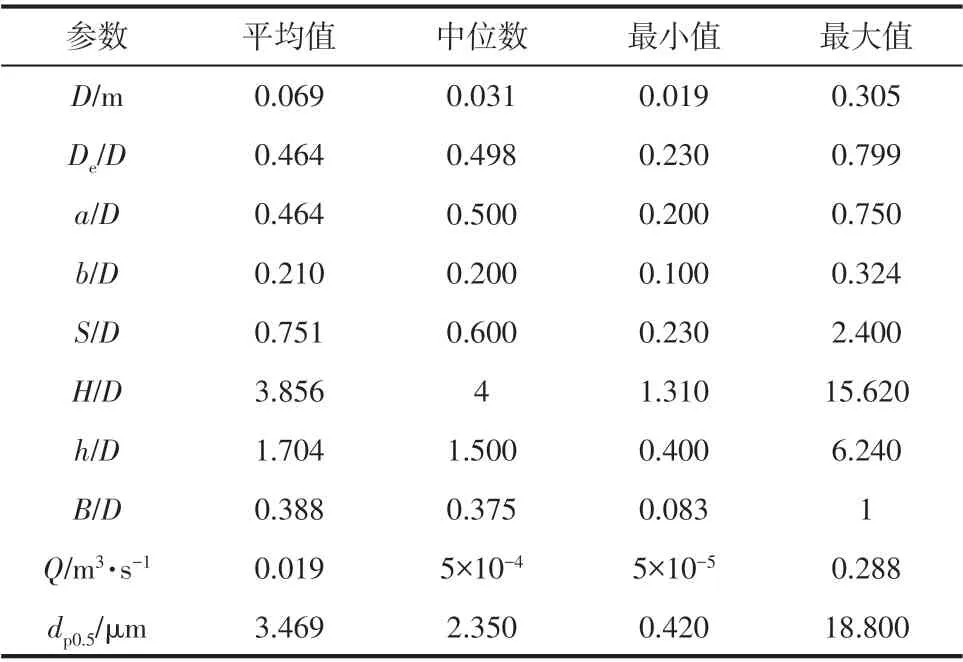
表1 數據集分布

1.4 評價指標

本文采用均方誤差（E2）、決定系數（R2）作為評價指標，如式(10)、式(11)所示。

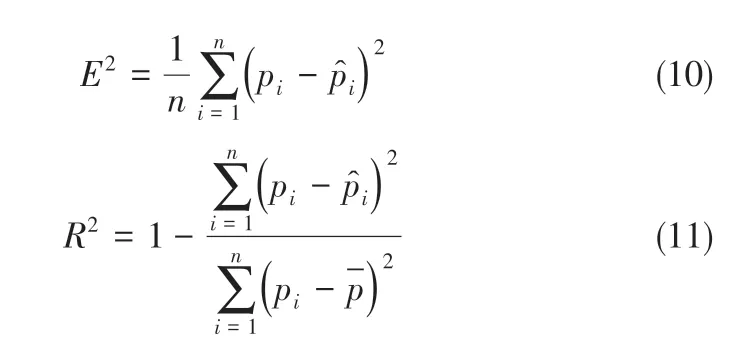
式中，n 為數據樣本數；pi為實測值；為預測值；為實測數據平均值。

2 結果與討論

2.1 神經元個數和訓練算法的影響

為了對比不同神經元個數和訓練算法對BP 神經網絡預測性能的影響，選用L-M 算法、擬牛頓算法、貝葉斯正則化算法進行預測性能的比較，每個訓練算法分別在隱含層神經元為6、7、8三個水平下對Ψ0.5進行預測。其中隱含層神經元個數為7的中間水平選取基于經驗公式2m+1，m 為輸入層神經元個數。為了避免網絡初始權值、閾值隨機性的影響，將每種組合的BP 神經網絡連續運行10次，選取評價指標的10 次均值進行評估，對訓練集和測試集預測的E2均值如圖2所示。

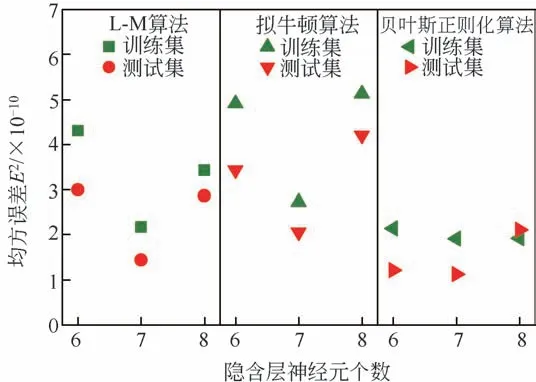
圖2 不同BP神經網絡模型E2比較

可以看到，在相同訓練算法下，采用不同隱含層神經元個數對訓練集和測試集的預測精度有影響。通過比較，在隱含層神經元個數為6、8時，各個訓練算法的E2均大于神經元個數為7時的E2。因此7為最佳隱含層神經元個數，L-M算法、擬牛頓算法、貝葉斯正則化算法均取得較優的預測性能，對訓練集預測的E2分別為2.175×10-10、2.725×10-10、1.919×10-10，對測試集預測的E2分別為1.446×10-10、2.064×10-10、1.121×10-10。

在隱含層神經元個數為7 時，從表2 中可以看到，3種訓練算法對訓練集和測試集預測的R2均大于0.95，表現出較好的預測能力。L-M算法對訓練集和測試集預測的R2分別為0.965、0.977，預測精度高于擬牛頓算法，略低于貝葉斯正則化算法。其中貝葉斯正則化算法展現出了最優的預測性能，對訓練集和測試集預測的R2分別為0.969、0.983。擁有自適應正則化參數的貝葉斯正則化算法能夠更好地規避網絡訓練時欠擬合和過擬合的問題，進而保障BP 神經網絡的魯棒性和泛化性能，本文選擇隱含層神經元個數為7 時基于貝葉斯正則化算法的BP 神經網絡建立BR(Bayesian regularization)-BPNN分割粒徑模型。

表2 不同訓練函數10次預測R2的均值

2.2 BR-BPNN分割粒徑模型性能

BPNN 初始權值、閾值的賦值具有隨機性，會造成每一次運行最終迭代的權值、閾值不同。為了確定BP 神經網絡的最優權值、閾值，應用BR-BPNN 分割粒徑模型對訓練集和測試集連續預測10次，對每次得到的E2進行比較。如圖3所示，可以看出第9次對訓練集和測試集預測得到的E2為10次中最小，分別為1.73×10-10、8.639×10-11。選用第9 次運行迭代出的權值、閾值作為BR-BPNN 分割粒徑模型的權值、閾值，詳細參數見表3，表中、、為輸入層的3 個神經元與隱含層的j個神經元之間的權值；為輸出層的1 個神經元與隱含層的j個神經元之間的權值；表示隱含層j個神經元的閾值；表示輸出層1 個神經元的閾值。

圖4 給出了BR-BPNN 分割粒徑模型預測值與旋風分離器分割粒徑實測值的比較。由圖可知，對訓練集和測試集中Ψ0.5的預測R2為0.972、0.987，BR-BPNN 分割粒徑模型展現出較高的預測精度。其中對測試集預測的R2高于訓練集，這表明經過訓練集訓練的神經網絡成功地推廣到測試集中，網絡的可靠性得到了證實。同時數據維度的減少提高了BR-BPNN 分割粒徑模型的質量，在訓練過程中能夠有效學習到數據特征，從而對新數據提供更好的預測能力。綜上所述，此模型可以作為一種新的預測模型對旋風分離器分割粒徑進行預測。

圖3 BR-BPNN分割粒徑模型10次預測E2對比

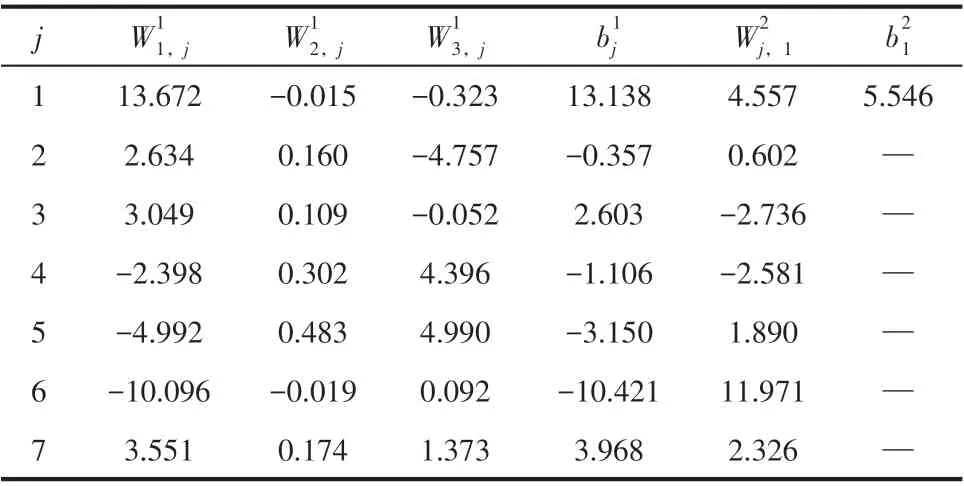
表3 BR-BPNN分割粒徑模型權值閾值參數

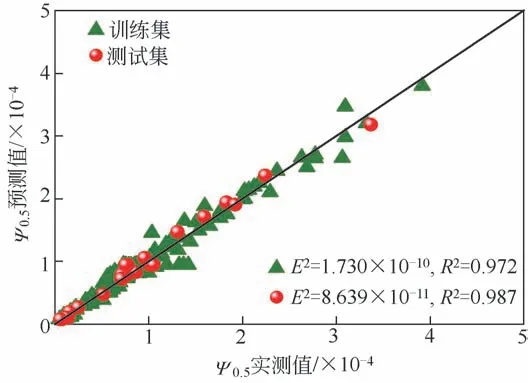
圖4 BR-BPNN分割粒徑模型預測值與實測值比較

2.3 不同分割粒徑預測模型性能比較

表4 給出了BR-BPNN 分割粒徑模型與其他分割粒徑模型的性能比較，樣本參數由本文測試集提供，預測結果統一換算為單位為μm 的dp0.5進行比較，其中多元回歸模型的回歸系數基于本文訓練集重新獲得。結果表明BR-BPNN 分割粒徑模型擁有最小的E2和最大的R2分別為0.136、0.975，預測精度最高。Lapple模型[6]、Barth模型[7]和Iozia等模型[8]的預測產生了較大的E2，分別為2.131、2.079 和3.872。多元回歸模型的預測精度較為相近，R2均大于0.94，略低于BR-BPNN分割粒徑模型。

在理論模 型 中，Lapple 模型[6]和Barth 模型[7]對復雜機理的數學描述需要通過模型簡化和假設實現。這會造成模型關鍵參數不易準確測得，如有效匝數、最大切向速度取值的偏差都會影響模型的預測性能。

表4 分割粒徑預測模型性能比較

在半經驗回歸模型中，Iozia 等模型[8]作為對Barth模型[7]的改進，通過使用部分尺寸參數和操作參數與內外渦交界面的寬度和最大切向速度建立聯系，并用實驗數據進行回歸得到系數。由于回歸系數的實驗數據僅來自筒體直徑D為0.25m的11組旋風分離器參數，相對于本文測試集包含筒體直徑范圍為0.019～0.305m 的24 組旋風分離器的參數而言，模型泛化能力的局限性導致了較低的預測精度。

在多元回歸模型中，Moore 等模型[27]取得了優于Lidén 等模型[11]的預測精度，R2為0.952。Lidén等模型[11]相較于Moore 等模型[27]關聯了更多的尺寸數，但忽略了除S/D 之外的尺寸參數，使得S/D 在因變量中所占權重過大，導致預測精度不高。Zhao等模型[9]通過構建全局尺寸參數關聯了所有結構尺寸參數和操作參數，在多元回歸模型中展現出較好的預測性能，但由于BR-BPNN 分割粒徑模型模化方式的先進性，相較于Zhao等模型[9]擁有更高的預測精度。

本文提出的BR-BPNN 分割粒徑模型的輸入參數不僅關聯了與旋風分離器切割粒徑有關的全部尺寸參數和操作參數，還將排氣芯管插入深度的尺寸比S/D進行了單獨關聯，提高了排氣芯管插入深度在因變量中的權重，以期對輸出參數有更合理的響應，同時BP 神經網絡又有著強大的非線性擬合能力，通過比較得出BR-BPNN 分割粒徑模型的預測性能更有優勢，對分割粒徑預測的泛化性能更好。

3 結論

（1）為了精確預測分割粒徑并更完全地表征其影響因素，在基于BR-BPNN 的分割粒徑模型的輸入參數中，環形空間雷諾數Reann耦合了操作參數Q和外部尺寸參數包括a、b 和De，基于等效體積法得到的等效分離距離量綱為1數Ds/D耦合了旋風分離器尺寸參數h/D、H/D、B/D，它們與S/D 一起反映了全部操作參數和結構尺寸參數對分割粒徑的綜合影響，可進一步對旋風分離器結構的優化設計提供參考。

（2）對BP神經網絡運行10次的預測性能均值分析表明，訓練算法和隱含層神經元個數對預測精度有影響。貝葉斯正則化算法作為訓練算法時，其預測精度高于L-M 算法和擬牛頓算法，同時在隱含層神經元個數為7時達到了較優性能，運用此組合建立BR-BPNN 分割粒徑模型對訓練集預測的R2=0.972，對測試集預測的R2=0.987，展現出較優的預測能力，作為分割粒徑的預測模型較為可靠。

（3）與已有的理論模型、半經驗模型和多元回歸模型比較，BR-BPNN 分割粒徑模型具有較高的預測精度和較全面的尺寸參數和操作參數的響應能力。