基于灰色關聯(lián)BP神經(jīng)網(wǎng)絡的壓縮式蓄冷系統(tǒng)中的水合物生成量預測

楊文宇，謝應明，閆坤，鄒俊華，舒勝

（上海理工大學能源與動力工程學院，上海200093）

CO2水合物作為一種新型蓄冷介質，具有蓄冷效率高、蓄冷密度大、傳熱效率高[1]、無毒[2]、環(huán)保及來源廣泛等優(yōu)點[3]，在蓄冷空調技術研究中得到國內外學者重視。作為蓄冷介質，水合物生成量對系統(tǒng)蓄冷量大小起決定作用。對于水合物的相平衡與生成量的預測研究，目前有經(jīng)驗、半經(jīng)驗模型和水合物理論預測模型可以對水合物的生成量進行預測。經(jīng)驗模型是利用實驗中的實際數(shù)據(jù)擬合得到的模型，計算簡單但精度不高，一般用于初步估算。理論模型是運用水合物生成時的動力學或熱力學理論，通過試驗得到的模型，預測誤差小但對理論模型要求較高，理論模型一直都是研究的重點。王樹立等[4]通過編程計算與實驗研究對比發(fā)現(xiàn)，化學親和力模型可準確預測復配體系水合物的生成。

近些年來，國內外學者利用諸如BP 神經(jīng)網(wǎng)絡模型、小波神經(jīng)網(wǎng)絡、馬爾科夫鏈預測、灰色理論等模型[5-8]建立了不同的水合物預測模型。神經(jīng)網(wǎng)絡在水合物的研究中應用十分廣泛，付康偉等[9]利用BP 神經(jīng)網(wǎng)絡算法建立陸域凍土地帶的天然氣水合物成藏模型，算法有效實用。馬金鳳等[10]根據(jù)地球化學數(shù)據(jù)建立水合物礦藏分類的神經(jīng)網(wǎng)絡模型，彌補了當前地球化學評價方法的部分缺點。Ghiasi等[11]通過利用最小二乘支持向量機及自適應模糊神經(jīng)推理系統(tǒng)等模型對CO2水合物的生成條件進行了研究，取得了良好的預測結果。Mesbah等[12]利用多層感知機神經(jīng)網(wǎng)絡建立了不同TBAB 濃度下的CO2水合物相平衡壓力模型，模型均方誤差僅為0.0596。考慮到單一模型在使用時較為容易，但其自身存在不同的局限性，適用性也有所不同，所以使用組合模型的方式將不同的模型組合起來使用，進而提高預測精度[13-14]。組合模型的方式有很多，如利用遺傳算法優(yōu)化BP 神經(jīng)網(wǎng)絡的模型[15]及利用粒子群算法優(yōu)化神經(jīng)網(wǎng)絡的模型等[16]。

CO2水合物生成的實驗過程表明，CO2水合物可以在無添加劑或有添加劑的情況下生成，不同添加劑體系下的反應時間不同[17]。CO2水合物的生成量和反應時間受多種因素的影響，包括壓力、初始溫度、添加劑濃度及攪拌方式等[18-20]，傳統(tǒng)的預測模型存在著計算復雜等缺點，因此建立一種適用性強的CO2水合物生成量預測模型是有必要的，可以解決預測CO2蓄冷系統(tǒng)水合物生成量的問題。

1 實驗系統(tǒng)及數(shù)據(jù)處理

1.1 實驗裝置

實驗裝置如圖1 所示，主要部件包括壓縮機、水冷式氣冷器、節(jié)流裝置、CO2直接接觸式反應釜、回熱器和其他輔助設備，如干燥過濾器等。數(shù)據(jù)采集系統(tǒng)包括溫度傳感器（精度為±0.15℃）、壓力傳感器（精度為±0.1%）、氣體質量流量計（精度為±0.1%）組成。系統(tǒng)數(shù)據(jù)采集由Agilent（安捷倫）系統(tǒng)完成。

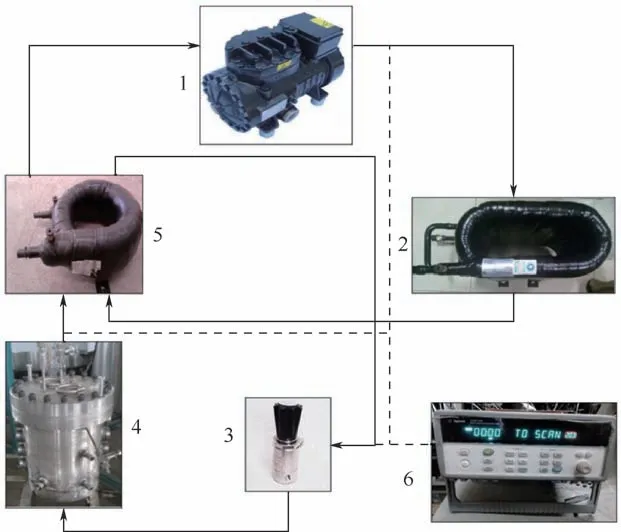
圖1 實驗裝置

1.2 數(shù)據(jù)處理

CO2水合反應方程如式(1)所示。

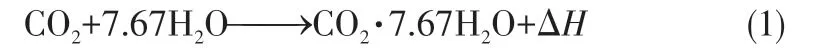
根據(jù)方程可以計算出水合反應所消耗水的質量mw,hyd，進而可以得到生成CO2水合物的質量，如式(2)所示。

1.3 實驗方法與工況

為了研究系統(tǒng)中水合物的生成特性及系統(tǒng)變量對水合物生成量的影響，實驗中設置3 個變量因素，分別為添加劑TBAB 濃度、CO2充注壓力和初始溫度。實驗用水為自來水，由上海市自來水市北公司提供；實驗用氣為純度99.99%的CO2，由上海市偉創(chuàng)標準氣體分析技術有限公司提供；實驗用添加劑為分析純濃度級別的TBAB，由中國國藥集團提供。具體的實驗方法是：①將9L水加入反應釜；②整體抽真空；③開啟反應釜處的恒溫槽使水溫達到要求的初始溫度，并且打開數(shù)據(jù)采集裝置；④充注CO2并達到指定壓力；⑤啟動壓縮機，實時觀察與記錄反應情況，并在數(shù)據(jù)顯示釜內下層溫度下降至0℃時關閉壓縮機等設備。實驗工況見表1。

表1 實驗工況

2 灰色關聯(lián)BP 神經(jīng)網(wǎng)絡預測模型的建立

2.1 灰色關聯(lián)預測模型基本介紹與構建

灰色模型是通過灰色量白化的方式，利用已知信息來預測未知信息的模型[21]。灰色關聯(lián)預測模型［GRM(1,n)］是在灰色預測模型［GM(1,n)］的基礎上，與灰色關聯(lián)度的概念相結合的組合預測模型，其具有利用少量樣本就可以得到精確結果的優(yōu)點[22]。灰色模型中運用最多的模型是以時間為序列建立的GM模型，將無規(guī)律的原始數(shù)據(jù)進行一次累加生成，記為1-AGO，簡稱累加生成，生成有規(guī)律的新數(shù)列，然后將新數(shù)列曲線擬合。考慮到影響水合物生成量的因素眾多，灰色模型的建立選用GM(1,n)模型，具體見式(3)～式(8)。

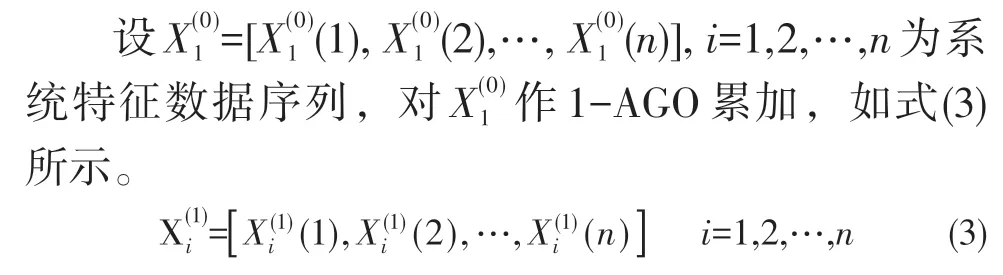
在GM(1,n)模型中，稱a為發(fā)展系數(shù)，稱bi為驅動系數(shù)，稱a^ 為參數(shù)列。參數(shù)列a^ 滿足式(4)。式(4)中，yN與B分別見式(5)、式(6)。

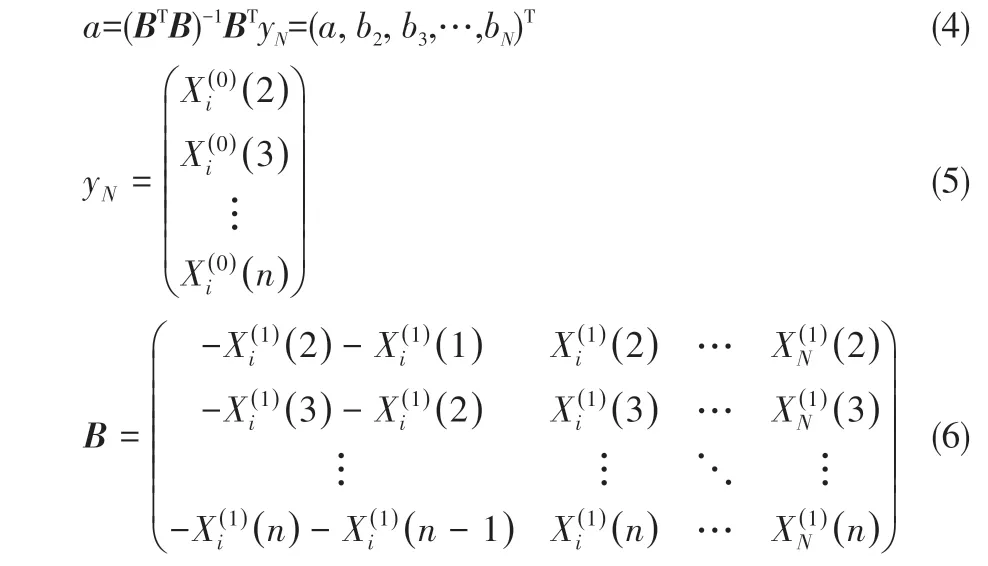
GM(1,n)模型的近似時間響應式見式(7)。

為了更好地分析不同影響因素對水合物生成量的影響度大小，需要進行灰色關聯(lián)分析。灰色關聯(lián)度的定義是：對于2個數(shù)據(jù)序列X1(0)和X2(0)，其灰色關聯(lián)度如式(9)所示。

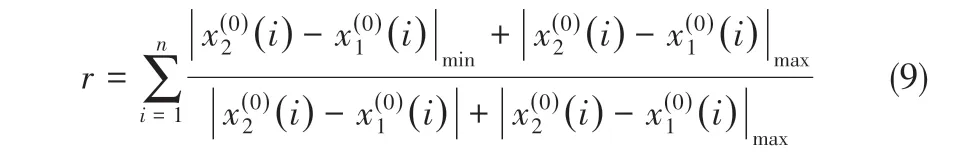
2.2 BP神經(jīng)網(wǎng)絡基本介紹與構建

BP 神經(jīng)網(wǎng)絡是在各領域中使用最普遍和有效的神經(jīng)網(wǎng)絡之一，屬于前饋神經(jīng)網(wǎng)絡的一種[23-26]。BP 會得到廣泛應用是因為其信號向前傳遞、誤差反向傳播的特點，在向前傳遞中，輸入信號從輸入層經(jīng)隱含層逐層處理，直至輸出層，若中間出現(xiàn)誤差則輸入到隱含層，以此類推，直到滿足誤差范圍，這樣使預測結果更加精準[27]。它的結構如圖2所示。

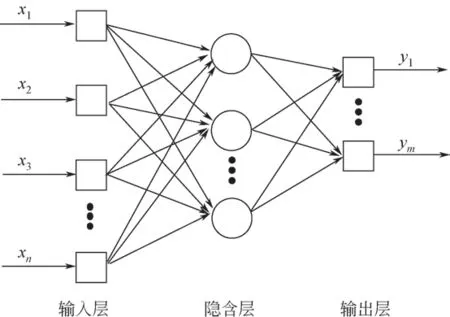
圖2 BP神經(jīng)網(wǎng)絡結構［28］

在構建BP神經(jīng)網(wǎng)絡前，需要將數(shù)據(jù)按照式(10)進行歸一化處理，使處理后的數(shù)據(jù)均勻分布在0～1之間。

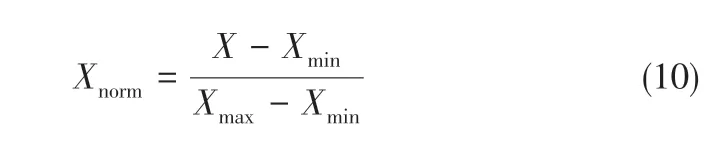
式中，Xnorm為歸一化后的值；X為輸入值；Xmax與Xmin分別為輸入值里的最大值和最小值。

在將數(shù)據(jù)進行歸一化處理后，將數(shù)據(jù)分為訓練和測試兩部分，利用Matlab 中的newff 函數(shù)構建BP神經(jīng)網(wǎng)絡。在模型得出結果后，需要將預測結果反歸一化得出預測最終結果。根據(jù)算法原理，BP 神經(jīng)網(wǎng)絡的3個主要參數(shù)為傳遞函數(shù)、隱含層神經(jīng)元個數(shù)和訓練函數(shù)。傳遞函數(shù)選擇tansig 函數(shù)，訓練函數(shù)選擇trainlm函數(shù)。

隱含層神經(jīng)元個數(shù)可根據(jù)式(11)來確定大致范圍。

式中，h 為隱含層神經(jīng)元個數(shù)；ni為輸入層神經(jīng)元個數(shù)；no為輸出層神經(jīng)元個數(shù)；m為(1,10)范圍內的常數(shù)。由式(11)可確定h的范圍為3～12。為了更好地確定網(wǎng)絡結構，在保持其他參數(shù)不變的情況下選取不同的隱含層節(jié)點數(shù)進行試算，結構如圖3所示。

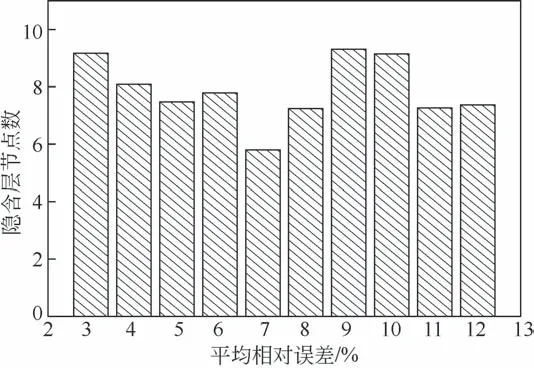
圖3 不同隱含層節(jié)點數(shù)預測結果的平均相對誤差

由圖3 可知，當隱含層節(jié)點數(shù)為7 時平均相對誤差最小，因此確定BP神經(jīng)網(wǎng)絡結構為3-7-1型，后續(xù)工作也基于此結構進行分析。

2.3 組合模型構建

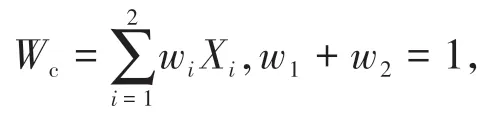
2.4 影響因素的灰色關聯(lián)度

根據(jù)灰色關聯(lián)度的定義，求得3個影響因素與水合物生成量的灰色關聯(lián)度，見表2。

表2 各影響因素與生成量的關聯(lián)度

灰色關聯(lián)度可以直觀反映出兩個因素變化趨勢的相似程度，灰色關聯(lián)度越大，相似程度越高。表格數(shù)據(jù)說明對水合物生成量影響最大的參數(shù)是充注壓力，其次是初始溫度與添加劑濃度。在實驗中，充注壓力的變化會直接改變參與水合反應的氣體質量，對水合物生成量影響最直接，初始溫度決定了反應的總體時長，而添加劑則是在前兩者確定的基礎上對水合物生成量的進一步提高，計算得出的關聯(lián)度大小符合實際情況。

2.5 灰色關聯(lián)預測模型預測結果

灰色預測方法具有可用少量數(shù)據(jù)得到較為精確的結果的優(yōu)點，本文選取15組工況數(shù)據(jù)進行預測，結果如表3所示。

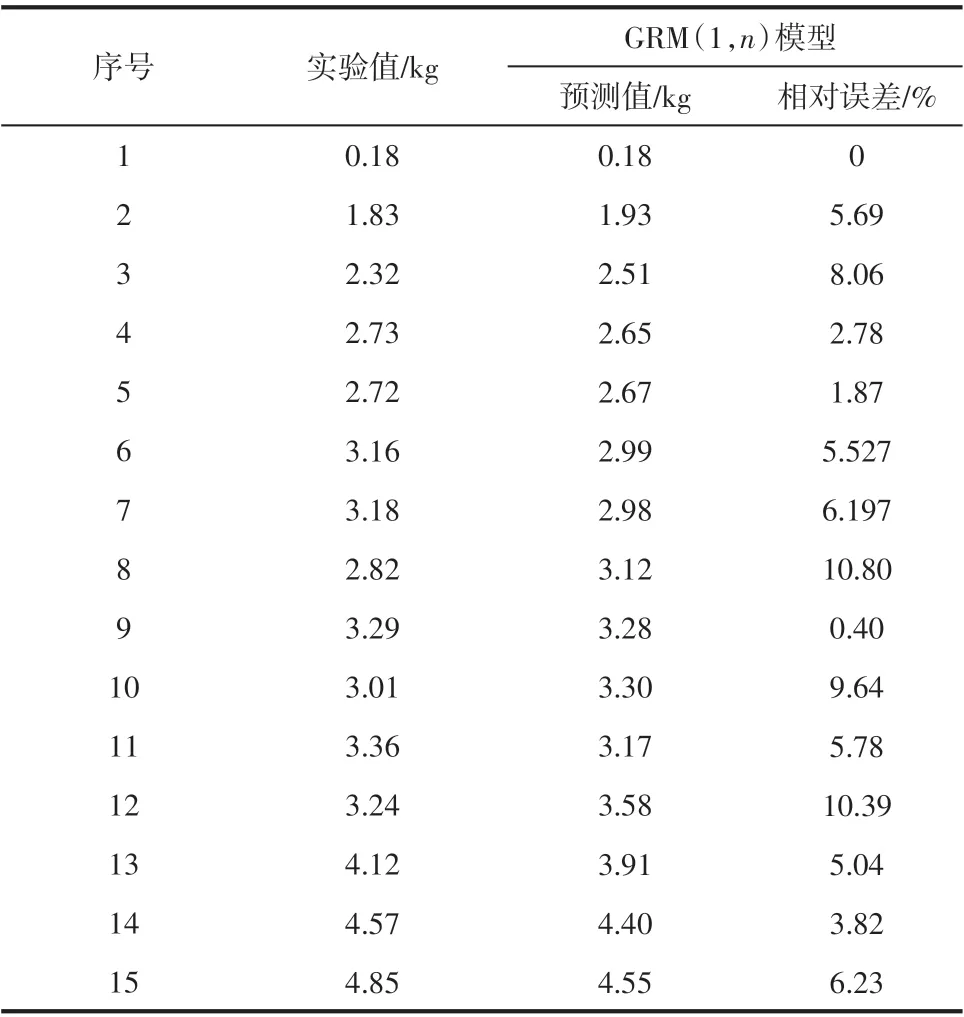
表3 灰色關聯(lián)模型預測結果

首先對GRM(1,n)模型的預測值進行后驗差檢驗：計算方差比c=S1/S2＝0.0353（其中S1、S2分別為原始序列和殘差的均方差），并且小殘差概率P=1，模擬值精度達到了一級標準，由此可知該模型可用于對系統(tǒng)水合物生成量預測。

2.6 BP神經(jīng)網(wǎng)絡預測結果

選取本文作者課題組累積的80 組數(shù)據(jù)作為訓練數(shù)據(jù)，15 組數(shù)據(jù)為測試數(shù)據(jù)，通過確定網(wǎng)絡的結構與參數(shù)進行訓練，預測結果見表4。

分析兩種單一模型結果可知，GRM(1, n)模型的平均相對誤差5.48%小于BP 神經(jīng)網(wǎng)絡模型的5.79%，BP 神經(jīng)網(wǎng)絡模型的最大相對誤差為13.52%，說明BP 神經(jīng)網(wǎng)絡在局部數(shù)據(jù)量較少的情況下精度較差，而GRM(1, n)模型對數(shù)據(jù)的需求量較少，最大相度誤差也小于13.52%。然而GRM(1,n)模型在數(shù)據(jù)量過多時效果較差，所以為了充分利用單一模型的有效信息，克服單一模型的缺陷，引入組合預測模型。

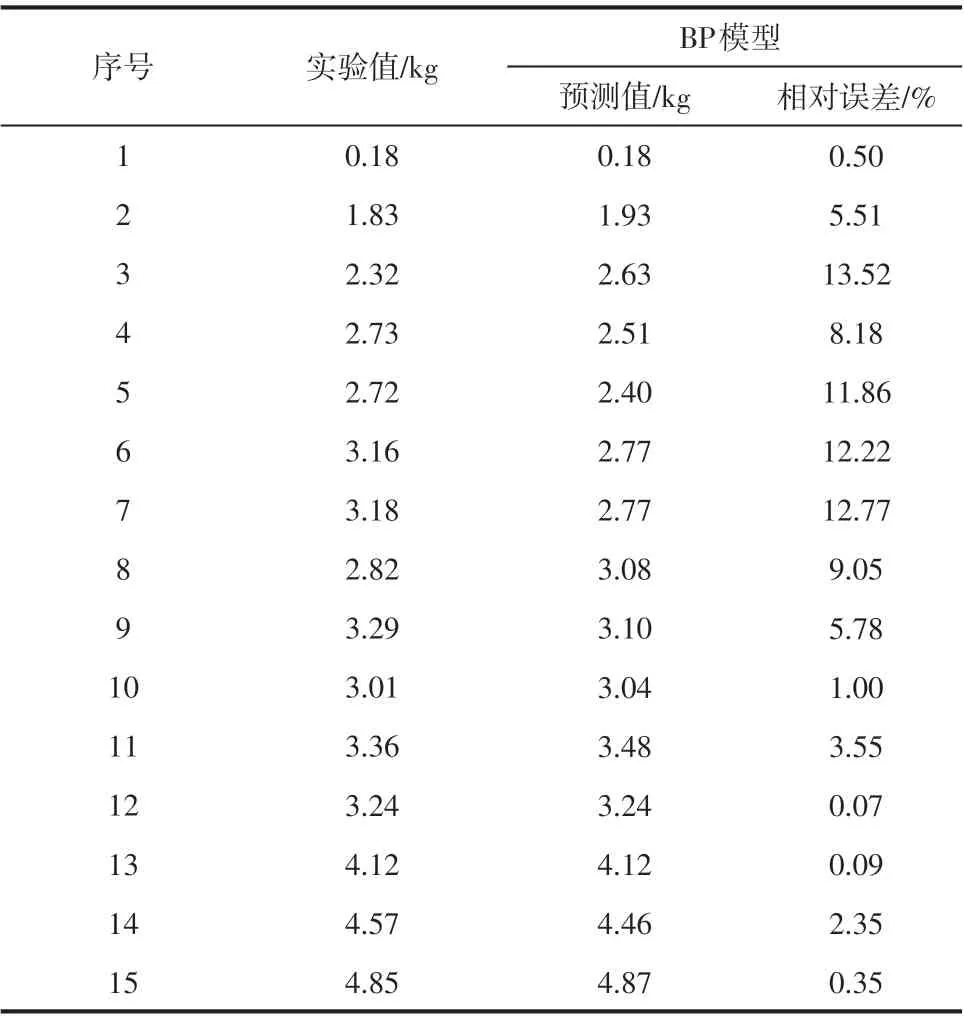
表4 BP神經(jīng)網(wǎng)絡模型預測結果

2.7 組合模型預測結果及比較

考慮到Matlab 程序編制簡單實用，依然選擇Matlab求解GRM(1,n)-BP神經(jīng)網(wǎng)絡組合模型，預測結果見表5。

從表3～表5 可以看出，組合模型具有較好的預測性，最大相對誤差10.78%比其余兩種模型小，平均相對誤差5.36%，也優(yōu)于單一模型。此外，GRM(1,n)模型、BP 神經(jīng)網(wǎng)絡模型及GRM(1,n)-BP組合模型的均方誤差分別為0.0411、0.0470 及0.0329。均方誤差可以評價數(shù)據(jù)的變化程度，其值越小，說明預測模型描述實驗數(shù)據(jù)具有更好的精確度。GRM(1, n)-BP 組合模型的均方誤差小于其余兩種單一模型，進一步驗證了組合模型預測結果更精確，且改善了個別預測誤差較大數(shù)據(jù)的擬合值，能更好地用來預測壓縮式系統(tǒng)CO2水合物的生成量。

2.8 組合模型驗證

基于上述分析，為了進一步驗證所建立的組合模型的適用性，利用GRM(1, n)-BP 神經(jīng)網(wǎng)絡組合模型對實驗裝置中的單一關鍵變量對水合物生成量的影響進行考察，基本思路為：使用標定的工況和操作方式，只改變添加劑TBAB 濃度、CO2充注壓力和初始溫度中的CO2充注壓力這一關鍵變量，將工況代入組合模型，得到水合物生成量的預測值。

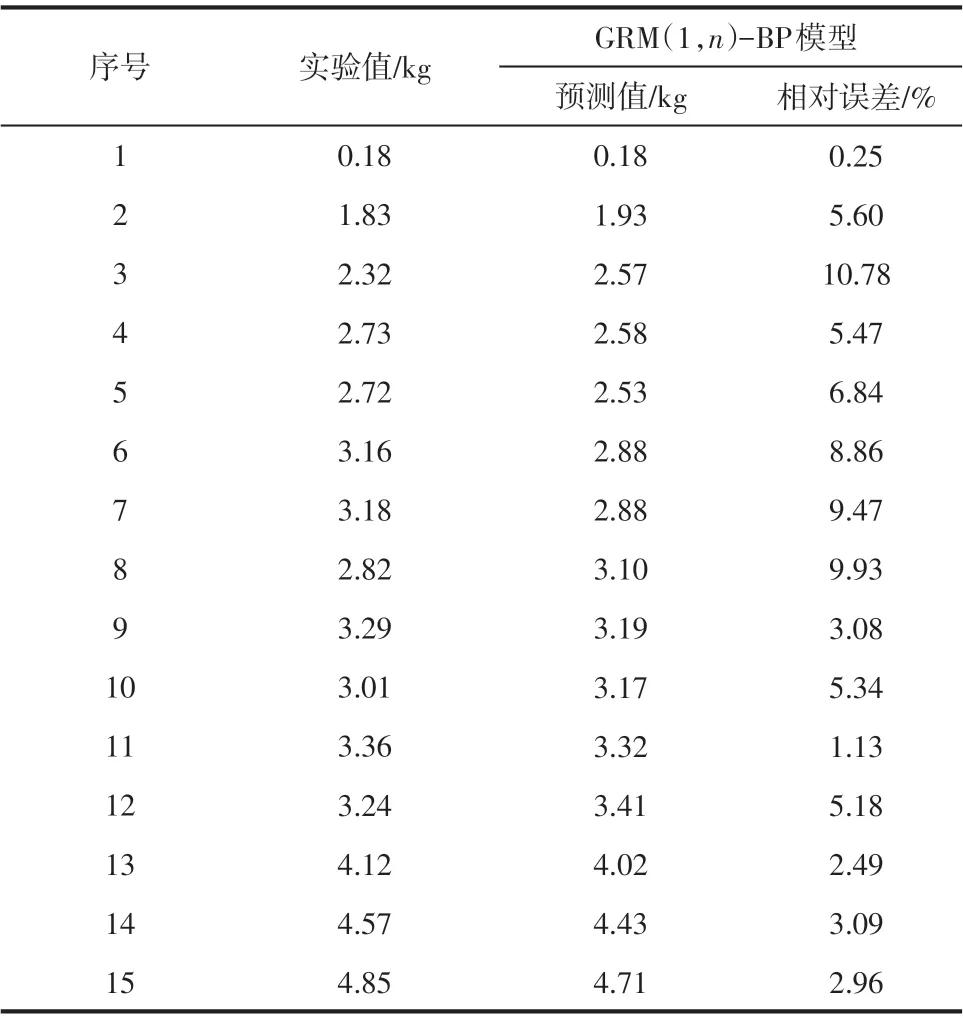
表5 組合模型預測結果

具體的工況：初始溫度為298.15K，TBAB 質量分數(shù)為15%，充注壓力為3.2～4.0MPa。將這一組工況代入GRM(1, n)-BP 神經(jīng)網(wǎng)絡組合模型，得到不同充注壓力下的水合物生成量。結果如圖4所示。

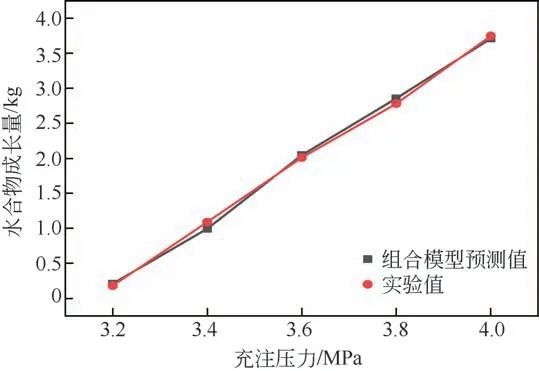
圖4 充注壓力對水合物生成量的影響

圖4表示了充注壓力對水合物生成量的影響情況，可見隨著充注壓力的增加，水合物生成量隨之增加。這是由于CO2含量不同會造成氣液間傳質效果出現(xiàn)差異，從而對水合反應產(chǎn)生較大影響，同時，由于CO2在本實驗中扮演著制冷劑的角色，其含量高低會造成制冷效果出現(xiàn)差異，從而影響系統(tǒng)的蓄冷總量和水合物生成量。結果表明，利用GRM(1, n)-BP 神經(jīng)網(wǎng)絡組合模型考察單一變量對水合物生成量的影響，其結果與實驗值平均誤差為6.56%，與反應機理也相符，進一步證明了預測模型的準確性。

3 結論

（1）基于實驗系統(tǒng)的數(shù)據(jù)，選取充注壓力、初始溫度及添加劑濃度作為3個影響參數(shù)，通過利用灰色模型需求數(shù)據(jù)量少、準確度高的優(yōu)點建立GRM(1, n)-BP 神經(jīng)網(wǎng)絡組合模型，對實驗系統(tǒng)中CO2水合物生成量進行了模擬，并對比分析了GRM(1,n)模型、BP 神經(jīng)網(wǎng)絡模型及GRM(1,n)-BP神經(jīng)網(wǎng)絡組合模型的預測誤差。

（2）仿真結果表明，GRM(1, n)-BP 神經(jīng)網(wǎng)絡組合模型能夠較為準確地預測實驗系統(tǒng)的水合物生成量，預測的平均相對誤差為5.36%，均方誤差為0.0329，與單一模型相比具有更好的預測性能。

（3）應用建立的GRM(1, n)-BP 神經(jīng)網(wǎng)絡組合模型考察了充注壓力對水合物生成量的影響，預測值與趨勢均符合實驗機理，進一步說明了所建模型的準確性。

（4）由于影響水合物生成的因素較多，在數(shù)據(jù)量更充足的情況下，模型能夠擁有更好的預測精度，使應用范圍更加寬廣。