基于反激式變換器的鋰電池組主動均衡電路
嚴 聰, 莫易敏*, 熊 巍,2
(1.武漢理工大學機電工程學院, 武漢 431600; 2.湖北工程學院機械工程學院, 孝感 432000)
隨著能源需求與環境污染問題的加劇,能量密度高、循環使用壽命長、自然放電率低、無記憶效應的鋰電池應用越來越廣泛[1-2]。然而由于鋰電池單體容量小,電壓低,需將多節單體電池串聯和并聯構成電池組以滿足實際使用需求[3-5]。由于現有的電池制造技術難以保持電池單體使用性能的一致性,且使用環境等影響因素會加劇不一致性[6],從而降低鋰電池組能量利用率,嚴重時甚至會造成安全問題。因此,需設計均衡系統,對鋰電池進行均衡控制,提高鋰電池組單體電池間的一致性[7-8],增加電池組的循環使用壽命,并提高其工作的安全可靠性。
目前鋰電池組的均衡電路拓撲結構可分為能量耗散型均衡(被動均衡)與非耗散型均衡(主動均衡)[9-10]。文獻[11]采用主被動均衡混合方式,可實現電池組均衡,但均衡時間長且被動均衡會導致能量損耗,降低能量利用率。文獻[12]提出基于多電感的均衡拓撲結構,能量只能在相鄰單體間轉移,需通過多次能量轉移實現電池組均衡,均衡時間長。文獻[13]提出一種混合式均衡拓撲結構,底層采用雙向Buck-Boost電路,頂層采用反激式變換器電路,結構簡單但均衡效率較低。參考文獻[14-16]提出基于單電感或單DC-DC變換器或單電容的均衡拓撲結構,可實現電池組和單體電池間的能量交換,但均衡時間長,效率低。文獻[17]提出一種基于附加電源的均衡電路,其結構簡單但均衡時負載電壓會有波動,且不適用于鋰電池組靜置或充電狀態。文獻[18]采用同芯多繞組結構,可實現非相鄰單體能量轉移,但均衡效率低耗時長。
鑒于目前鋰電池組主動均衡多采用相鄰單體間能量轉移或單體與電池組間能量轉移方式,所用均衡時間長,為有效改善均衡效率,綜合上述多種均衡拓撲結構,提出一種基于反激式變換器的均衡拓撲結構,以耦合電感作為儲能元件,高能量電池單體通過均衡模塊將能量轉移至其余電池單體。反激式變換器自身電氣隔離,各均衡模塊可同時工作。結構簡單,易于實現模塊化且能快速實現均衡是其主要優點,并通過建模仿真驗證了該拓撲結構的有效性及高效性。
1 均衡拓撲結構與工作原理
1.1 均衡拓撲結構
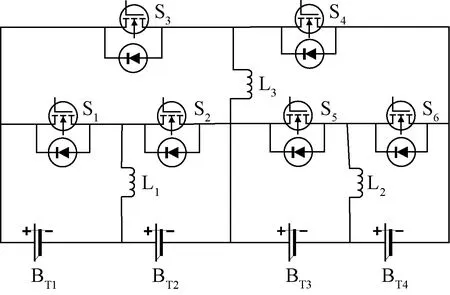
提出的基于反激式變換器的鋰電池組均衡拓撲主要由四節單體電池、4組耦合電感及若干金屬氧化物半導體場效應晶體管(metal oxide semiconductor field effect transistor,MOSFET)組成,其均衡拓撲結構如圖1所示。

圖1 基于反激式變換器的均衡電路Fig.1 Equalization circuit based on flyback converter
圖1中,BT1、BT2等表示電池單體,S1、S2等表示MOSFET管,Li,j(i=1,2,3,4;j=1,2)表示第i組耦合電感,j=1時為原邊繞組,j=2時為副邊繞組。該均衡電路共有4個均衡模塊,耦合電感L1,1與L1,2構成均衡模塊1,可實現BT1與BT2-BT2-BT4之間的能量交換;耦合電感L2,1與L2,2構成均衡模塊2,可實現BT2與BT3-BT4之間的能能量交換;耦合電感L3,1與L3,2構成均衡模塊3,可實現BT3與BT1-BT2之間的能量交換;耦合電感L4,1與L4,2構成均衡模塊4,可實現BT4與BT1-BT2-BT3之間的能量交換。反激式變換器本身可以實現電氣隔離,且各均衡模塊有對應繞組,所形成的充放電回路是相互獨立的,多個模塊可以同時進行均衡,能夠有效提高均衡效率。
1.2 均衡拓撲工作原理
基于反激式變換器的鋰電池組均衡拓撲的均衡模塊基本工作原理如圖2所示。圖2中,BTH和BTL分別表示高能量電池單體和低能量電池單體,以電池組由BTH向BTL充電為例進行說明:開關管S1導通、S2斷開,電流從BTH流出,經變換器的原邊繞組L1回到BTH負極,由于S2斷開,副邊回路中無電流,BTH釋放電能轉換為磁能存儲在耦合電感中。開關管S1和S2均斷開時,原邊繞組L1內電流消失,副邊繞組通過續流二極管與電池BTL形成回路,變換器中的磁能轉換為電能釋放,給BTL充電。
反激式變換器工作模式可分為斷續電流模式(DCM)和連續電流模式(CCM):連續模式下峰值電流小,平均電流大,開關管損耗小,但原邊電感過大會影響負載電流變化響應速度,且系統不穩定;斷續模式下,副邊峰值電流大約為連續模式電流的2~3倍,對負載電流變化響應速度更快且系統非常穩定[19]。因此,所設計反激式變換器工作模式為斷續電流模式。反激式變換器拓撲如圖3所示,VH、VL表示高能單體電壓和低能單體電壓,L1、L2為一組耦合電感。工作在斷續電流模式下流過耦合電感原邊、副邊繞組的電流波形圖如圖4所示。圖4中,i1和i2表示流過L1和L2的電流,I1max和I2max表示其最大值。
設耦合電感原邊繞組與副邊繞組的匝數為N1和N2其匝比為N1∶N2=1∶1,原邊繞組勵磁電感(L1)與副邊繞組勵磁電感(L2)的大小均為Lm,開關管開關頻率為f,占空比為D,周期為T。開關管S1導通至DT時刻,此時原邊繞組電流線性上升,S1關斷后,副邊繞組電流線性下降,下降至Te(Te≤T)時刻,電流降為0。

圖2 均衡模塊工作原理圖Fig.2 Working principle diagram of the balance module

圖3 反激式變換器拓撲結構Fig.3 Flyback converter topology

圖4 耦合電感原邊、副邊繞組電流波形圖Fig.4 Coupling inductance primary and secondary current waveform
當0≤t≤DT時:
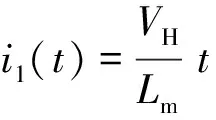
(1)
當DT≤t≤Te時:
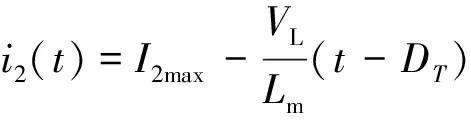
(2)
當t=DT時,原邊繞組電流值與副邊繞組電流均達到最大,可分別表示為

(3)

(4)
當t=Te時,i2(Te)=0時可得

(5)
因此有
(6)
1.3 均衡拓撲控制策略
在均衡電路控制中,常用均衡變量有鋰電池單體電壓、電池荷電狀態(state of charge,SOC)以及電池容量。以鋰電池單體荷電狀態SOCi(i=1,2,3,4)作為均衡變量,均衡開啟條件為
Δ=max{SOCi}-min{SOCi}>0.05
(7)
式(7)中:Δ表示電池組中最高能量單體與最低能量單體間的SOC差值。若滿足式(7),則開啟均衡,比較相鄰單體間的SOCi,以下列策略進行均衡。
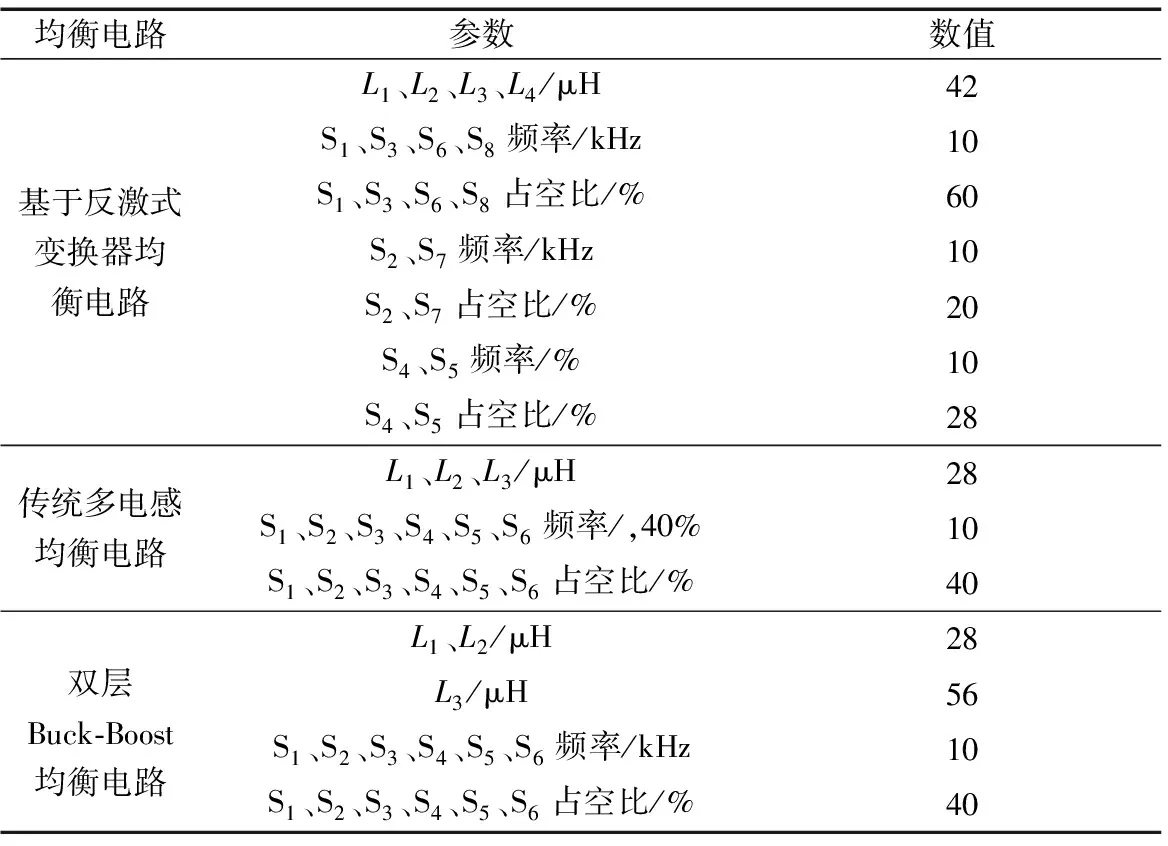
比較SOC1與SOC2:若SOC1>SOC2,S1工作,BT1給BT2-BT3-BT4充電;若SOC1 比較SOC2與SOC3:若SOC2>SOC3,S3與S5工作,BT2給BT3-BT4充電,BT1-BT2給BT3充電;若SOC2 比較SOC3與SOC4:若SOC3>SOC4,S7工作,BT1-BT2-BT3給BT4充電;若SOC3 為驗證所建立的基于反激式變換器的鋰電池組均衡電路的可行性與高效性,將其與傳統的多電感均衡電路和基于雙層Buck-Boost均衡電路進行仿真對比。傳統多電感均衡電路拓撲如圖5所示,以電感作為儲能元件,可實現相鄰單體電池間的能量轉移;基于雙層Buck-Boost均衡電路拓撲如圖6所示,分為內層均衡電路和外層均衡電路,其以兩個單體電池為一組,內層通過電感實現組內相鄰單體電池間的能量轉移,外層通過電感實現組間電池組能量轉移。 圖5 傳統多電感均衡電路Fig.5 Traditional multi-inductor equalization circuit 圖6 雙層Buck-Boost均衡電路Fig.6 Double-layer Buck-Boost equalization circuit 在MATLAB/Simulink中搭建仿真模型,單體電池標準電壓為3.7 V,容量為2 Ah,4個單體的荷電狀態SOC初始值分別為90%、85%、80%、75%,單體電池容量為2 Ah,分別對鋰電池組靜置、以0.3 ℃倍率充電和以0.6 ℃倍率放電三種狀態進行仿真。仿真時,各電感、耦合電感允許最大電流不超過6 A。各均衡電路元件主要參數分別如表1所示。 靜置狀態下3種均衡電路的SOC隨時間變化曲線圖如圖7所示。仿真結果表明,3種均衡電路均能實現鋰電池組在靜置狀態下的均衡,均衡時間分別為158.711、458.152、232.050 s。 表1 各均衡電路元件主要參數表 圖7 靜置狀態下SOC變化曲線Fig.7 SOC change curve under static state 由圖7可知,3種均衡電路在靜置狀態下的過程分析可知:對于基于反激式變換器的均衡電路,在0~61 s內,4個均衡模塊同時工作,能量快速從BT1、BT2轉移至BT3、BT4;61~150 s內,均衡模塊1、4工作,BT2與BT3可等效于靜置,能量從BT1轉移至BT4,由于仍有兩個模塊同時工作,此時仍可保持較高均衡效率;150~159 s內,均衡模塊1工作,能量由BT1轉移至BT2、BT3和BT4,此時由于4個單體SOC差異很小,因此,盡管均衡效率有所下降,但均衡耗時短。 對于傳統多電感均衡電路,0~240 s內,3個電感同時工作,可等效于能量從BT1轉移至BT4,由于能量只能單向傳遞且經過了3次轉移,因此均衡效率低,此過程中BT2與BT3的SOC因轉移過程中的能量損耗略有下降;240~458 s內,3個電感均工作,此時等效于將BT1、BT2中能量較高者轉移至BT3、BT4中的能量較低者,由于BT1與BT2交替向低能量單體充電,因此均衡效率降低、耗時長。 對于雙層Buck-Boost均衡電路,在0~120 s內,3個電感同時工作,此時可等效于能量從BT1轉移至BT4,由于BT1可通過內層和外層均衡來轉移能量,因此相較于傳統多電感均衡電路均衡效率有所提高;120~232 s內,電感L3工作及外層均衡電路工作,能量從BT1-BT2轉移至BT3-BT4,由于能量只經過一次傳遞,因此其均衡效率相較于傳通過電感電路較高。 以0.3 C倍率給電池組充電狀態下3種均衡電路的SOC隨時間變化曲線圖如圖8所示。仿真結果表明,3種均衡電路均能實現鋰電池組在充電狀態下的均衡,均衡時間分別為158.325、454.688、230.996 s。 圖8 充電狀態下SOC變化曲線Fig.8 SOC change curve under charging state 由圖8可知,3種均衡電路在充電狀態下的過程分析如下。對于基于反激式變換器的均衡電路,在0~58、58~149、149~158 s 3個時間段內4個均衡模塊的工作狀況與上述靜置狀態時工作狀況一致。此時由于對電池組進行充電,在58~149 s內BT2和BT3的SOC持續上升。對于傳統多電感均衡電路,在0~240、240~455 s兩個時間段內各電感的工作狀況與上述靜置狀態時工作狀況一致。此時由于對電池組進行充電,在0~240 s內BT2和BT3的SOC持續上升;240~455 s內,BT1、BT2的均衡放電電流與充電電流大小相等,因此其SOC基本不變。對于雙層Buck-Boost均衡電路,在0~119、119~231 s時間段內各電感的工作狀況與靜置狀態時保持一致。此時由于對電池組進行充電,在0~191 s內,BT2和BT3的SOC持續上升;119~231 s內BT1和BT2的均衡放電電流大于充電電流,因此SOC持續下降。 圖9 放電狀態下SOC變化曲線Fig.9 SOC change curve under discharging state 以0.6C倍率給電池組放電狀態下3種均衡電路的SOC隨時間變化曲線圖如圖9所示。仿真結果表明,三種均衡電路均能實現鋰電池組在放電狀態下的均衡,均衡時間分別為159.799、461.618、233.328 s。 由圖9可知,3種均衡電路在放電狀態下的過程分析可知,對于基于反激式變換器的均衡電路,在0~58、58~151、151~160 s時間段內4個均衡模塊的工作狀況與上述靜置狀態時工作狀況一致。此時由于對電池組進行放電,在58~151 s內BT2和BT3的SOC持續上升。 對于傳統多電感均衡電路,在0~243、243~462 s兩個時間段內各電感的工作狀況與上述靜置狀態時工作狀況一致。此時由于對電池組進行放電,在0~243 s內BT2和BT3的SOC持續下降;243~462 s內,BT3、BT4的均衡充電電流小于放電電流,因此其SOC持續下降。 對于雙層Buck-Boost均衡電路,在0~121、121~233 s時間段內各電感的工作狀況與靜置狀態時保持一致。此時由于對電池組進行放電,在0~191 s內,BT2和BT3的SOC持續下降;119~231 s內BT3和BT4的均衡放電電流略大于充電電流,因此SOC基本保持不變。 由上述3種均衡電路在靜置、充電、放電狀態下的仿真結果及過程分析可知,3種均衡電路均能實現電池組均衡功能,降低單體電池間的差異性。從而避免某一優先充滿能量或優先釋放完能量而導致的整個電池組無法繼續充電或放電的狀況發生。 且提出的基于反激式變換器均衡電路相較于傳統多電感電路和基于雙層Buck-Boost均衡電路,其在整個均衡過程中均衡充放電電流最大。因此,在整個均衡過程中,基于反激式變換器的均衡電路均衡效率最高,基于雙層Buck-Boost均衡電路均衡效率次之,傳統多電感均衡電路均衡效率最低。 3種電路在電池組處于不同狀態時,所用均衡時間均有差別。相較于靜置狀態,在充電狀態下3種電路的均衡時間均有所縮短,分別為0.386、3.464、1.054 s。造成這種差異的原因是對電池組充電會使得單體電池電壓上升,從而使得均衡電流變大,提高均衡效率。但因為均衡時間短,電壓上升幅度較小,因此這種差異不大。在放電狀態下3種電路的均衡時間均有所增加,分別為1.088、3.466、1.278 s。造成這種差異的原因是對電池組放電會使得單體電池電壓下降,從而使得均衡電流減小,降低均衡效率。但因為均衡時間短,電壓下降幅度較小,因此這種差異不大。 (1)介紹了基于反激式變換器的均衡電路,以耦合電感作為儲能元件,對該電路進行了工作原理分析,并制定相應控制策略。同時,對反激式變換器工作單電流斷續模式下進行了分析。 (2)搭建了均衡電路仿真模型,對鋰電池組靜置、充電及放電三種狀態進行仿真,驗證了該均衡電路及控制策略的可行性。將其與傳統多電感均衡電路和基于雙層Buck-Boost均衡電路對比,仿真結果表明在三種狀態下所提出的均衡拓撲電路所用均衡時間最短,效率最高。2 仿真試驗結果及分析

2.1 靜置狀態仿真及過程分析
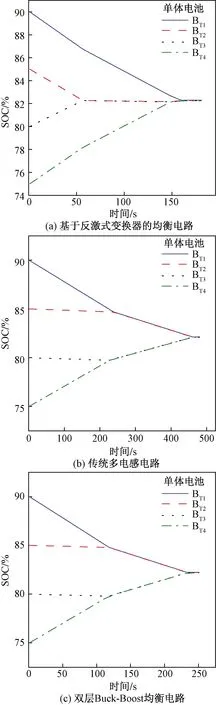
2.2 充電狀態仿真及過程分析

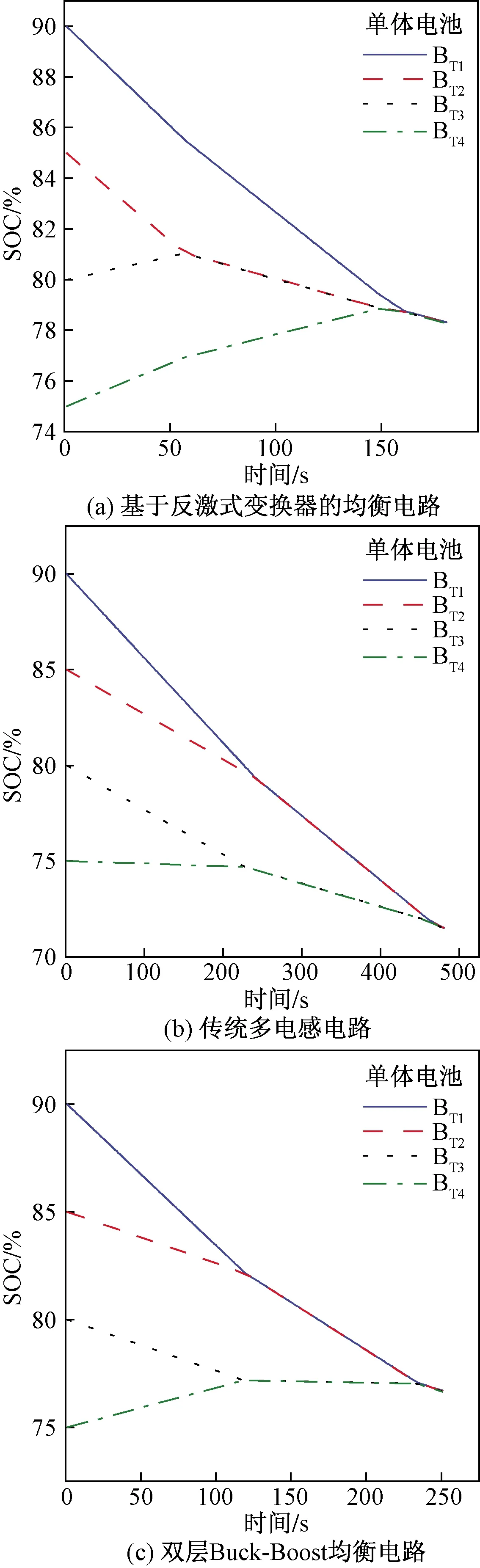
2.3 放電狀態仿真及過程分析
2.4 結果分析
3 結論

