體液無機離子在鎂表面的腐蝕機理

劉小娥, 馬保吉

(西安工業(yè)大學機電工程學院, 西安 710021)

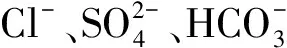
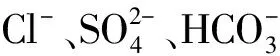
1 模型

1.1 力場模型

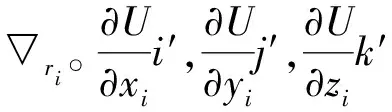
Fi=-riU(r1,r2,…,rN)=

(1)

1.2 勢能模型

采用模擬體系為金屬和無機離子兩種模擬體系相混合的復雜模擬體系,模擬所選取的力場為Compass力場及Reaxff力場。用Compass力場和用Reaxff力場計算時體系總勢能、粒子總勢能的計算公式分別為[10]

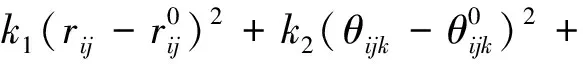
(2)

E=Ebond+ELP+Eover+Eunder+Eangle+Edihedral+

EvdW+Eq

(3)

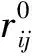
2 模擬體系的構建與模擬方法

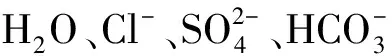
由于鎂的密排六方晶格結構,選取其密排面Mg(0001)面進行研究。在構建Mg(0001)晶胞結構時,為了驗證所采用方法和模型的合理性,首先構建鎂的單晶胞,如圖2(a)所示。然后采用Castep模塊對鎂的單晶胞進行結構優(yōu)化[13],優(yōu)化后三條邊長尺寸為a=b=0.322 nm,c=0.517 nm,a、b為單晶胞底邊邊長,c為單晶胞的高,實驗值a=b=0.320 nm,c=0.521 nm[14],優(yōu)化后的結果與實驗值非常接近。取Mg(0001)面,如圖2(b)所。然后構建Mg(0001)表面超晶胞結構,體系的尺寸為31.56 nm×31.56 nm×27.38 nm,如圖2(c)所示。體系包含1 584個鎂原子。在模擬過程中,由于金屬1～3層原子容易發(fā)生明顯的弛豫現(xiàn)象,因此固定Mg(0001)晶胞四層以下的原子作為相體原子,上面的三層原子設置為可自由移動[15]。

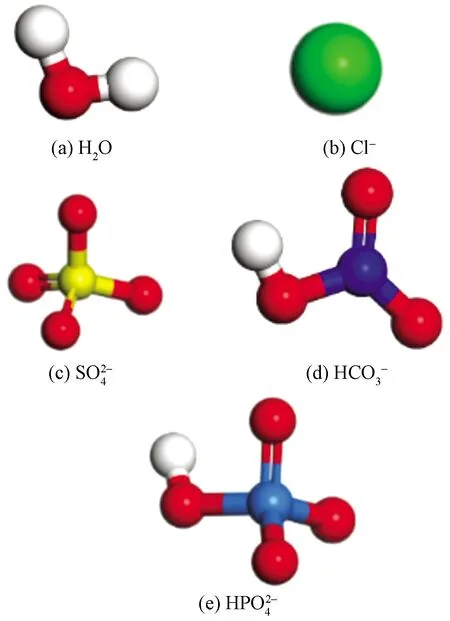
圖1 各離子模型結構優(yōu)化結果Fig.1 Structure optimization results of each ion model

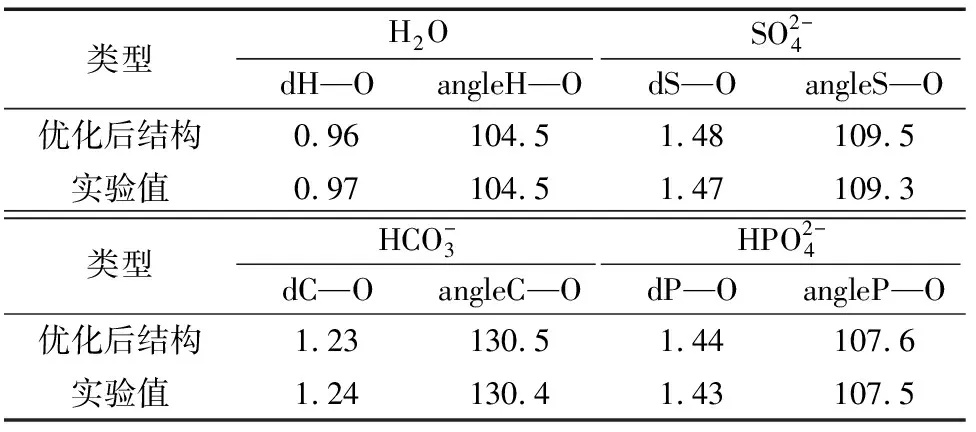
表1 不同離子優(yōu)化結構與實驗值[15]

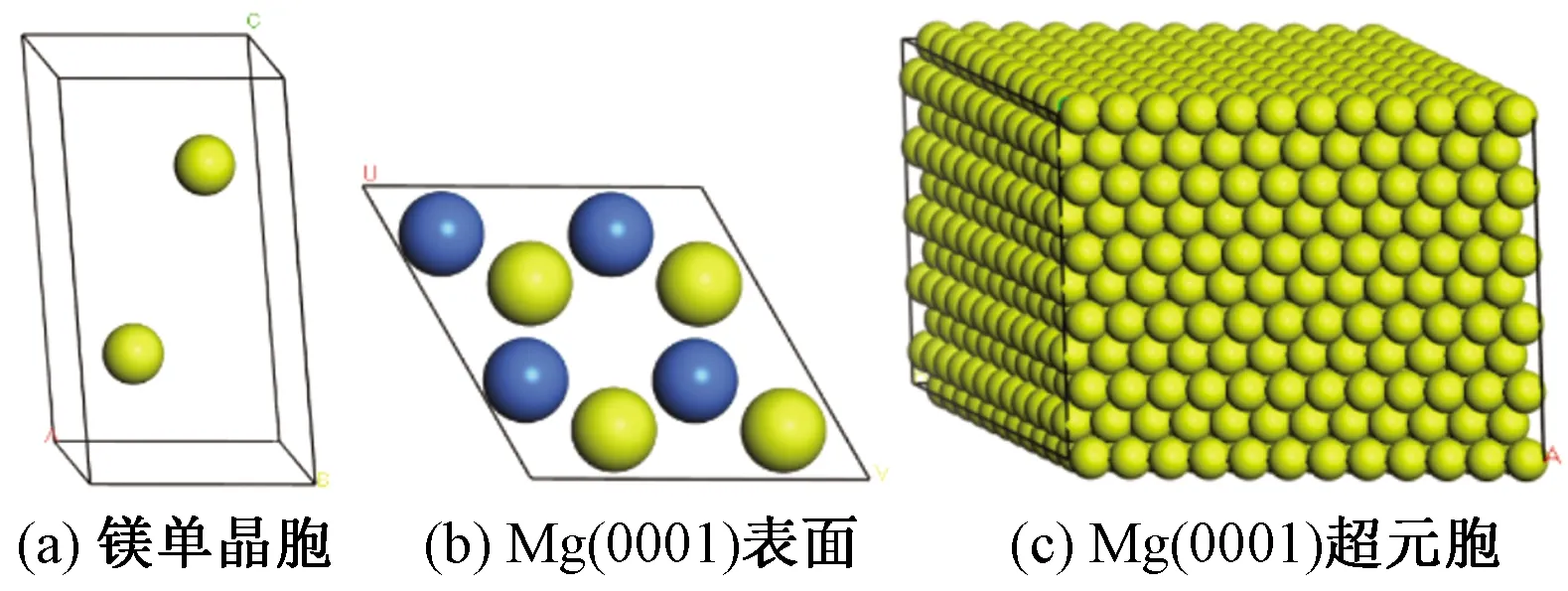
圖2 Mg(0001)晶胞結構的構建Fig.2 Construction of cell structure of Mg(0001)

腐蝕離子在Mg(0001)表面的擴散行為模擬采用正則系綜(NVT)[17],模擬溫度為310 K,控溫方式為Andersen[16],范德華和庫侖相互作用的計算方法為Ewald[17]。選取的截斷半徑為0.5 nm。模擬步長為1 fs,總時長為200 ps,每500步記錄一次軌跡信息(幀)[18-19]。

圖3 4種腐蝕離子在Mg(0001)表面的擴散體系模型Fig.3 Diffusion system model of four corrosion ions on the surface of Mg(0001)

3 模擬結果與分析

3.1 體系平衡的判斷

在分子動力學模擬中,用溫度平衡條件和能量平衡條件來判斷體系平衡[20]。以Cl-離子溶液作用于Mg(0001)表面的模擬模型為例,圖4、圖5分別為在310 K溫度下,Cl-離子溶液作用于Mg(0001)表面的模擬體系進行NVT模擬的溫度變化和能量變化。

從圖4可見,體系的溫度波動平穩(wěn)。從圖5可見,在模擬過程中,前40 ps體系能量降低至能量最低態(tài),40 ps后體系的能量波動和偏差較小,此后體系已達到平衡。溫度和能量計算結果符合溫度平衡條件和能量平衡條件,這表明此模擬體系的建立及計算過程合理、結果分析可靠。

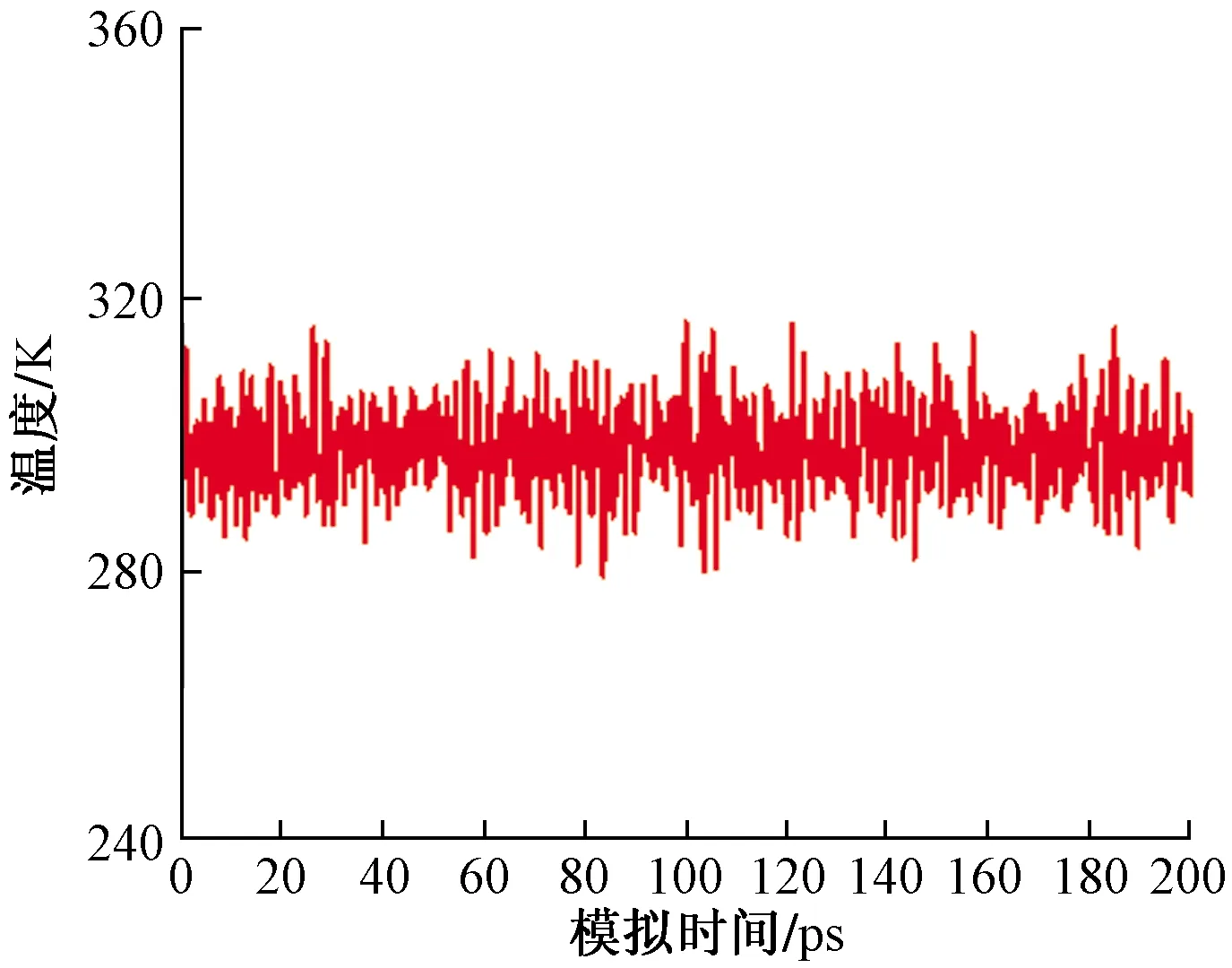
圖4 模擬過程中溫度隨時間變化Fig.4 Temperature changes with time in the simulation process

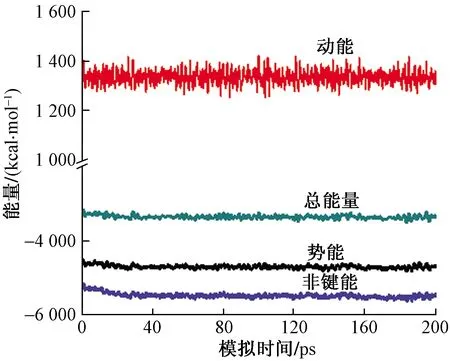
圖5 模擬過程中能量隨時間變化Fig.5 Energy changes with time in the simulation process

3.2 無機離子在Mg(0001)表面的擴散特性

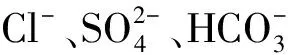
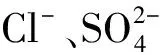
擴散系數(shù)(diffusion coefficient,DC)是表征4種無機離子作用于Mg(0001)模擬體系中擴散行為的重要參數(shù)。擴散系數(shù)的函數(shù)表達式為[21]

(4)

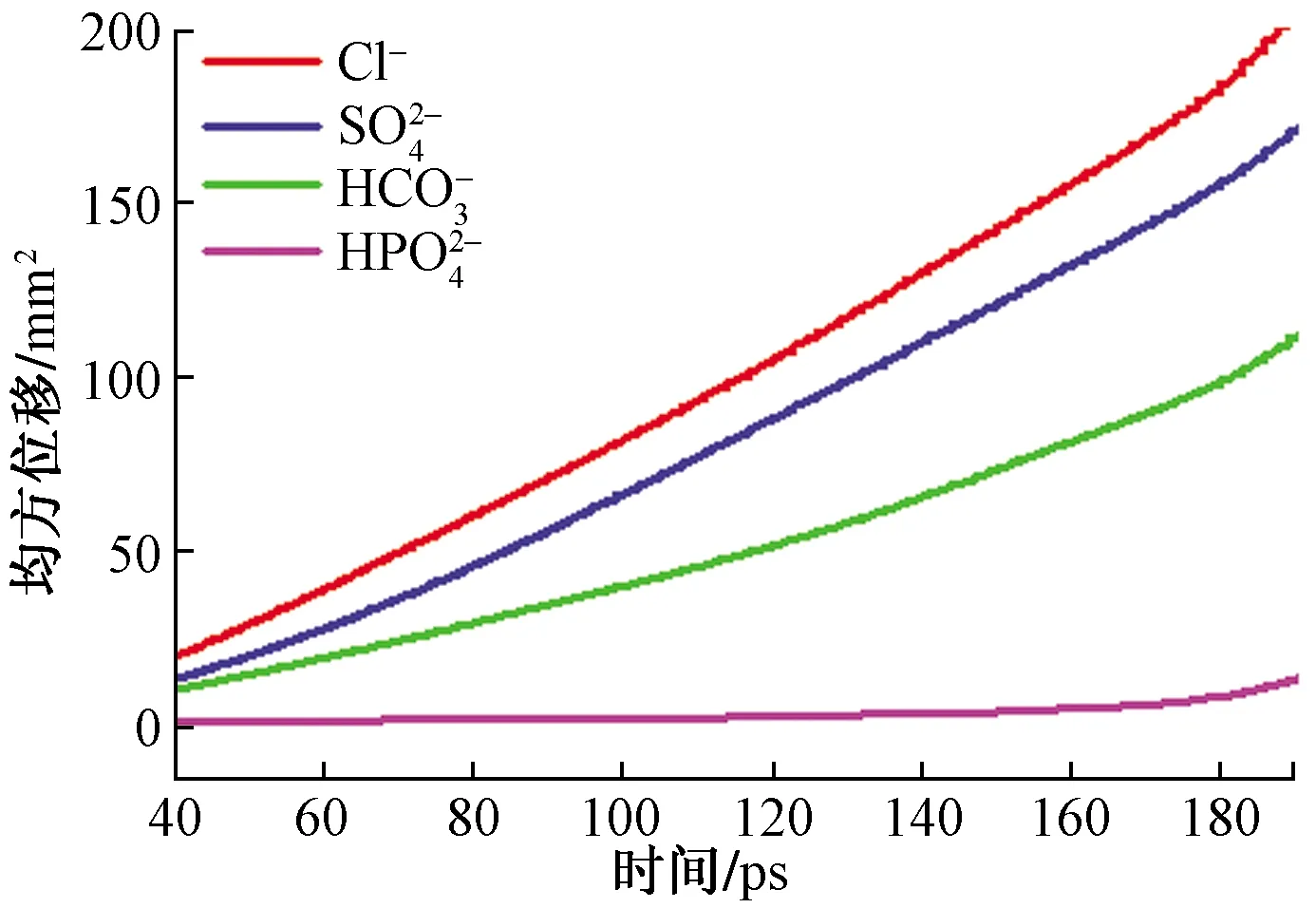
圖6 不同離子作用于Mg(0001)表面的MSDFig.6 MSD of Mg(0001) surface with different ions

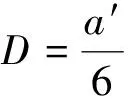
(5)

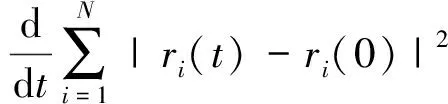
3.3 徑向分布函數(shù)

徑向分布函數(shù)(radial distribution function,RDF)用g(r)表示,其表達式為[22]

(6)

式(6)中:NM為分子數(shù)目；T為總步數(shù)；δr為距離差；ΔNM為r→r+δr分子數(shù)目。

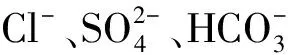
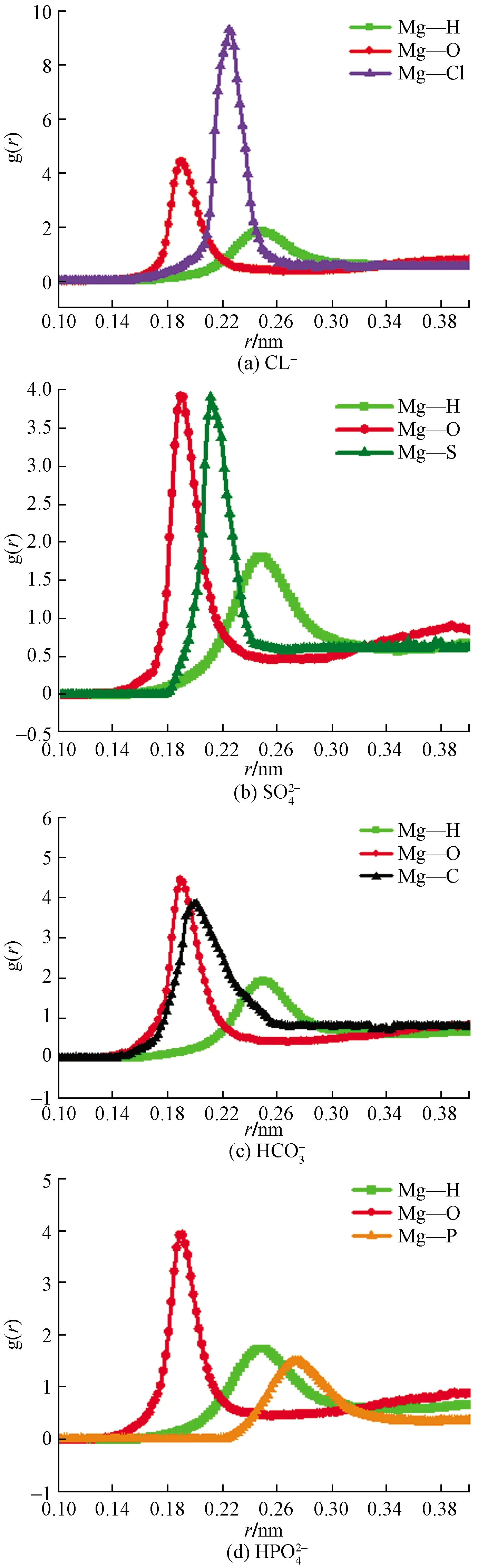
圖8 不同離子子作用于Mg(0001)表面原子間的g(r)～rFig.8 g(r)～r of different ions acting on the surface atoms of Mg(0001)

3.4 無機離子在Mg(0001)表面的反應產(chǎn)物

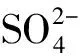
4 實驗驗證

4.1 模擬濃度計算

通過計算模擬體系后的離子濃度和實驗所得的離子濃度是否相同來驗證模擬體系的可靠性。通過模擬體系所得的反應產(chǎn)物含量可計算出不同模擬體系中每個鹽離子的平均濃度，其平均濃度計算公式為

(7)

式(7)中：n為物質(zhì)的量；N為離子數(shù)；NA為阿伏伽德羅常數(shù),其值為6.02×1023；V為體積,單離子作用下模擬體系的尺寸為172 ?×172 ?×420 ?=1.24×10-23L；c為濃度，mol/L。

采用紫外-可見光譜分析法可以測得物質(zhì)的吸收程度,物質(zhì)的吸收程度可用Beer-Lambert定律描述[23]為

A=εbc

(8)

式(8)中:A為溶液吸光度；ε為該溶液摩爾吸光系數(shù),L/(mol·cm);b為吸收池液體厚度,cm；c為溶液濃度,mol/L。

表2 單一離子溶液作用于Mg(0001)表面的濃度Table 2 Concentration of a single ionic solution on the surface of Mg(0001)

結合紫外光譜實驗對模擬勢能模型、模擬體系的構建及模擬結果的可靠性加以驗證。

4.2 實驗方法

實驗前,將純度為 99.5% NaCl、Na2SO4、NaHCO3及Na2HPO4在80 ℃下干燥48 h,由去離子水配置10% NaCl溶液、Na2SO4溶液、NaHCO3溶液及Na2HPO4溶液各15 L；配置好溶液后去除溶液中的氧氣；試樣為含鎂量為99.9%的鎂片,試樣的尺寸為10 mm×10 mm×1 mm,用不同的SiC砂紙對試樣進行逐級打磨,然后超聲清洗。

采用恒電位法進行實驗,將處理后的鎂片作為工作電極,選用鉑電極作為輔助電極。分別浸泡在NaCl溶液、Na2SO4溶液、NaHCO3溶液及Na2HPO4溶液中進行電壓為5 V,時長為5 min的電化學實驗,實驗后將反應后的溶液放置在試管中保存。

4.3 實驗結果及分析

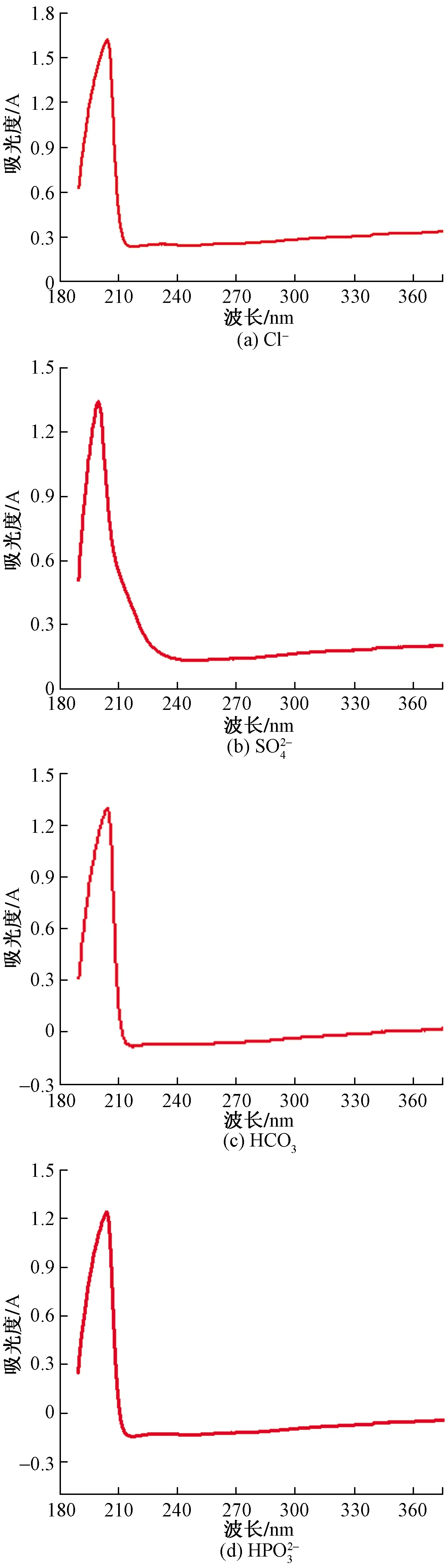
圖10 單一離子溶液作用于純Mg表面的紫外光譜Fig.10 Ultraviolet spectrum of a single ionic solution on a pure Mg surface

利用式(8)得到參與電化學反應后的不同離子溶液所對應的濃度(c)如表3所示。

得到參與電化學反應后的不同離子溶液所對應的離子濃度如表4所示,為了直觀比較模擬結果與實驗結果,表4中同時列出了模擬計算結果。

表3 單一離子溶液所對應的濃度Table 3 Concentration of a single ionic solution

表4 單一離子溶液所對應的濃度Table 4 Concentration of a single ionic solution

對比發(fā)現(xiàn),經(jīng)過對比發(fā)現(xiàn),模擬結果和實驗結果吻合,所建模擬模型及模擬計算結果正確。

5 結論

(2)不同離子溶液作用于Mg(0001)表面模擬體系的腐蝕程度不同的主要原因在于,加入不同的腐蝕離子以后,四個不同的模擬體系所形成的化學鍵Mg—O的強度不同。其次,Mg—Cl間的相互作用力、Mg—S間的相互作用力、Mg—C間的相互作用力和Mg—P間的相互作用力的不同也是其腐蝕程度不同的重要原因。

(4)模擬體系的濃度和實驗所得的濃度吻合,故在模擬過程中所建立的勢能模型及模擬體系正確,模擬結果可靠,該模擬方法可以作為體液中無機離子在鎂表面擴散特性的有效手段。