基于GWR模型的共享單車空間分布影響因素分析

楊逍遙，王建軍，李國棟，程小丹

（1.長安大學運輸工程學院，陜西西安 710061；2.陜西市政建筑設計研究院有限公司，陜西西安 710021）

0 引言

近年來，隨著國家大力提倡綠色出行，越來越多的市民選擇共享單車作為出行“最后一公里”的交通接駁工具或短途代步工具。共享單車受到用戶青睞的同時也面臨如何合理投放、管理及配置基礎設施等問題。共享單車借、還車行為在空間上的分布差異不僅受出行者個人屬性的影響，還在很大程度上受騎行環境、停放環境、車輛管理狀況等的影響。厘清各影響因素對單車分布的作用機理，深入了解單車出行特征及時空分布規律，可為共享單車的投放、調度、運營管理及騎行環境的改善提供解決思路。

國內外學者對自行車及共享單車出行分布特征及其影響因素進行了大量研究。在自行車出行分布特征研究方面，出行的時間分布特征主要表現為時間的波動性，相關研究有：Vogel 等提出一種基于每個用戶的單車使用強度與規律的聚類方法，研究發現周末出行人數較工作日少，且周末出行客流曲線較為平緩，無明顯的客流高峰現象[1]；莫海彤等以廣州市為例發現共享單車在工作日具有明顯的早晚高峰，休息日的出行高峰為午間及傍晚[2]；郭海富等根據共享單車使用時間分布提出靜態與動態結合的調度方式[3]。在共享單車出行的空間分布特征方面，周榮等運用數理統計法研究了共享單車空間分布，發現企業更愿意將共享單車投放在商業發達區域[4]；魏宗財等研究發現工作日共享單車出行集中于交通樞紐及教育科研功能區，休息日主要分布于商圈[5]；陳奇放等基于GIS空間分析法對共享單車騎行OD路線進行分析，發現隨著距離的增加，集聚現象呈減弱趨勢[6]；楊蒙等將不同的功能用地空間按共享單車分布密度進行分類，分析了分布特征與用地之間的內在機理[7]。為更好地解釋共享單車出行的空間異質性，了解共享單車出行對周圍空間變化的敏感性，Contardo 等為實現單車的重新分配提出了基于Dantzig-Wolfe 分解算法和Benders分解算法的調度優化模型[8]。而國內研究大多從共享單車的騎行數據出發來研究單車出行的分布特征[2,9]，較少考慮外在因素對單車出行的影響差異，鮮有研究量化分析外在環境因素與共享單車出行分布特征間的非穩定性作用規律。

在對自行車出行分布特征影響因素的研究中，國外學者在數據提取、因素考量、模型創新等方面進行了很多嘗試[10-15]。Corcoran 等利用空間分析技術結合模型回歸與度量方法對澳大利亞布里斯班的城市自行車系統數據進行分析，以探索周末、節假日等特殊時段及天氣因素對公共自行車出行時空分布特征的影響，分析發現強風和降雨明顯減少了自行車出行次數[16]。國內方面，曾小利等通過建立主要的騎行起點和終點熱力圖，發現短距離出行受城市主干路的影響較大，跨區域出行共享單車數量受土地利用和土地利用混合度影響較大[17]；李煜茜等從宏觀、中觀、微觀3 個層面對共享單車騎行影響因素進行研究，發現道路環境、立體環境和道路功能是影響騎行適宜性的3 大主要因素[18]；高楓等通過引入地理探測器發現服務類設施對共享單車的影響最為顯著，其次是交通可達性、自然環境類別[19]。已有研究大多基于核密度[17]、普通最小二乘法（Ordinary Least Squares,OLS）[16,18]進行回歸分析判別各種因素對于共享單車出行分布的影響，假設全局參數一致，沒有考慮空間因素與影響因素之間的關系，對于空間位置差異性研究較少。

為了更好地解釋空間異質性，Brunsdon 提出了地理加權回歸模型（Geographically Weighted Regression,GWR）[20]，該模型因具有良好的擬合優度得以廣泛應用，如用于解釋出租車客流[21]、公交客流[22]的空間分布等。為了更好地衡量不同區域截面參數的空間異質性，本文引入地理非平穩性概念，通過GWR 模型來分析外在因素對共享單車分布特征的影響及其空間異質性。

1 數據來源與影響因素選取

本文擬采用共享單車GPS 數據來分析共享單車的出行分布特征。共享單車數據主要來源于Python 每5min 爬取到的2018 年9 月28 日（星期五）整個西安地區停放的某品牌單車GPS 位置數據，獲取的數據字段包括采集時間、單車編號、單車經緯度，示例見表1。

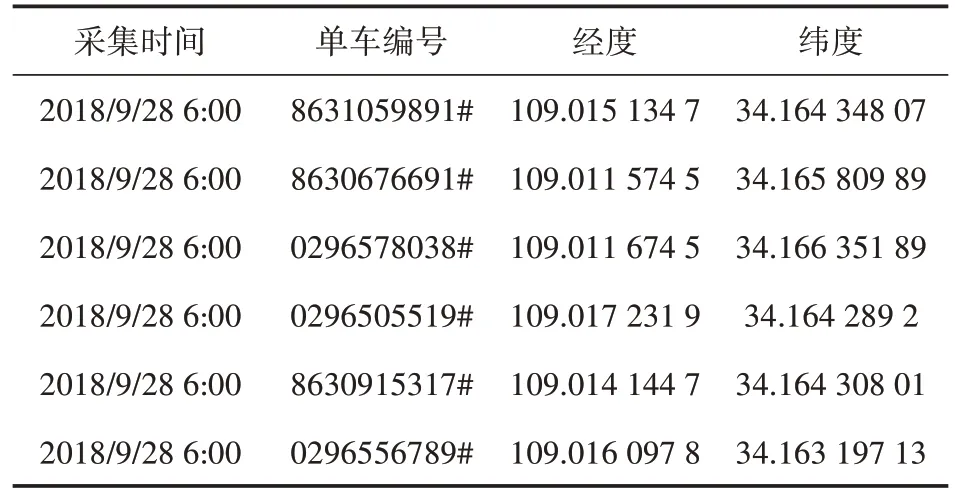
表1 原始數據示例

從研究區域的社會、經濟、基礎設施等實際狀況出發，結合已有文獻中對自行車騎行特征及其影響因素的探究，總結分析得到以下4 類影響因素。

（1）用車環境。已有研究表明共享單車停放點的數量與容量的增加會促進單車出行[11]。此外，共享單車設施（主要指出行產生前交通小區內的共享單車）分布密度與非機動車道的覆蓋情況在很大程度上決定著用戶的二次騎行意愿，因此用車環境是否便捷舒適成為了解共享單車出行分布特征的一個重要指標。

（2）道路交通基礎設施。城市道路等級密度、長度、連通性等指標將直接影響用戶體驗及對出行方式的選擇，進而影響單車分布狀態。有學者就不同類型的道路長度對共享單車出行的影響進行了分析，認為主干路的長度會對單車出行產生負面影響，而支路長度在一定程度上會促進單車出行[23]。

（3）公共交通變量。共享單車停放點與交通樞紐點（如火車站、客運站、軌道交通或常規公交站點）間的最短路徑長度、共享單車停放點輻射區內的公交站點數量和類型等指標在不同程度左右著出行者對出行方式的選擇。若共享單車與其他公共交通站點銜接并不理想，可能對騎行產生負面影響。

（4）土地利用變量。根據已有研究可知，就業情況對共享單車的分布具有一定影響[24]，而土地利用影響具體的就業分布。此外，土地利用類型較為多樣化的區域將會有較高的出行需求產生[23]，常用的生活服務設施、消費場所及休閑娛樂場所等其他服務設施的分布差異也會引起共享單車出行起訖點有規律地差異分布。

綜合上述分析，依據所需數據采集的難易程度及數據可靠性，選取能反映研究區域內共享單車分布特征的影響指標，如圖1所示。

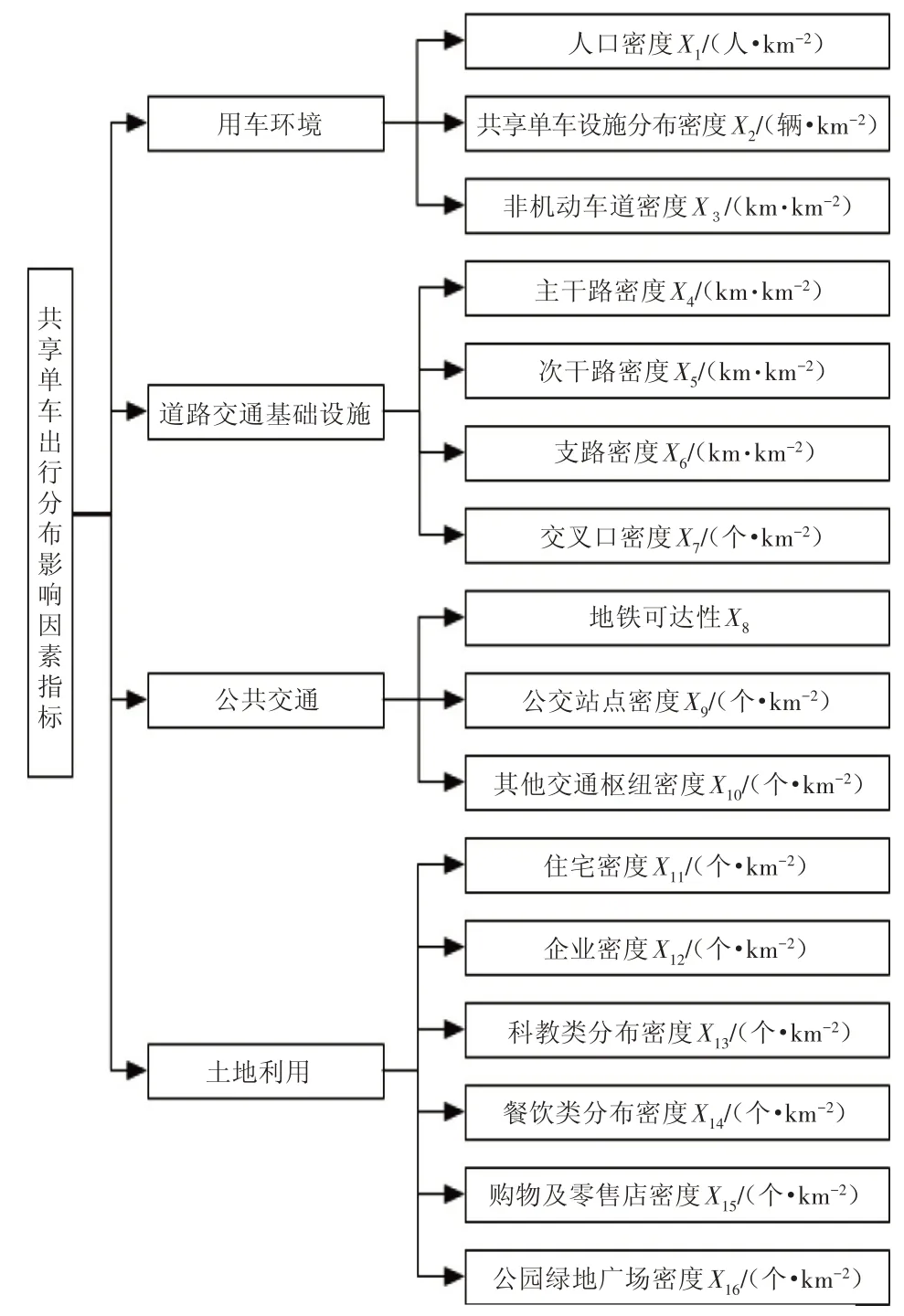
圖1 共享單車出行分布的影響因素

圖1 所示影響因素中，共享單車設施分布密度指出行產生前交通小區內的單車分布密度；人口數據和城市路網等矢量數據來源于西安市城市交通模型，經過提取計算得到各小區的目標要素；X9～X16均為對獲取的興趣點（Point of Interest,POI）數據進行處理后得到的有效數據；地鐵可達性SubAr的計算公式[25]為：

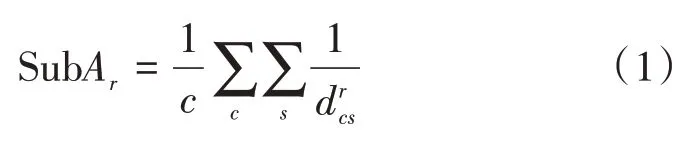
2 模型建立

本文首先建立多元線性回歸模型對影響因素進行全局回歸分析，初步篩選得出影響較為顯著的變量。考慮到部分因素隨著時間及空間的變化，其對因變量的影響程度也會有所差異，故進一步通過構建地理加權回歸模型（GWR），對變量進行空間異質性檢驗，并比較這兩種回歸模型的擬合效果。

2.1 全局回歸模型

在進行多元線性回歸時，為避免參數估計值發生嚴重偏差，需對備選自變量間的多重共線性進行檢驗，以保證解釋變量的獨立性，提高模型估計的準確度。本文采用方差膨脹因子（Vari?ance Inflation Factor，VIF）作為檢驗工具，以剔除不符合要求（VIF較大）的影響因子。

多元線性回歸模型用兩個或多個自變量來解釋因變量的變化，且可以用普通最小二乘法（OLS）求解各變量對應的系數。該模型計算公式為：

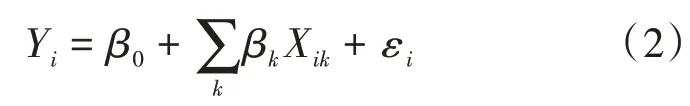
式（2）中：Yi為第i個樣本點的因變量（早晚高峰單車出行起訖點）；β0為線性回歸方程的截距（常數項）；βk為第k個自變量（影響因素）的回歸系數；Xik為第i個樣本點的第k個自變量；εi為隨機誤差項。

2.2 地理加權回歸模型

空間顯著性相關是GWR 模型的使用前提條件，為便于后續空間計量經濟模型的構建與參數估計分析，本文采用Moran′s I（莫蘭指數）對各解釋變量進行空間自相關性分析。Moran′s I 是用來度量空間相關性的一個重要指標，經歸一化處理后，取值為（-1,1）。Moran′s I大于0表示空間正相關，其值越大則空間相關性越強；Moran′s I小于0 表示空間負相關，其值越小則空間差異越大；Moran′s I 等于0，表示空間不具有相關性。GWR模型是在傳統線性回歸模型的基礎上改造模型系數，納入表示地理位置的參數，根據研究區域的空間變化對各變量進行局部回歸分析。本文選用GWR 模型對共享單車空間分布的影響因素進行進一步探討，其計算公式為[20]：

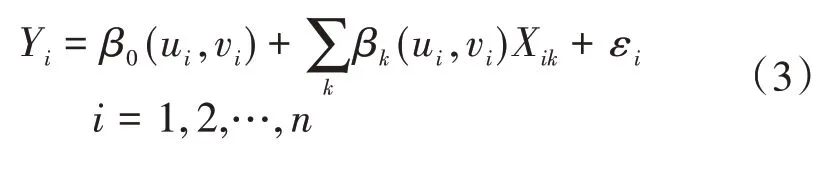
式（3）中：(ui,vi)為第i個樣本點的空間經緯度坐標點；εi為隨機誤差項，εi～N(0,δ2),Cov(εi,εj)=0(i≠j)；n為樣本量。

模型的實現流程如下：

（1）確定最優帶寬。帶寬b用來解釋wij（空間權重）與dij（樣本點i與j距離）之間的函數關系。帶寬b過大將會導致不同區域間的參數估計值差異不明顯，影響模型參數估計值的準確性；而過小的帶寬則會導致方差變大[21]。赤池信息準則（Akaike Information Criterion,AIC）是衡量統計模型擬合優良性的標準之一，本文選用修正后的AIC，即AICc 來確定最優帶寬，當函數值AICc最低時，模型最優，AICc計算公式為：

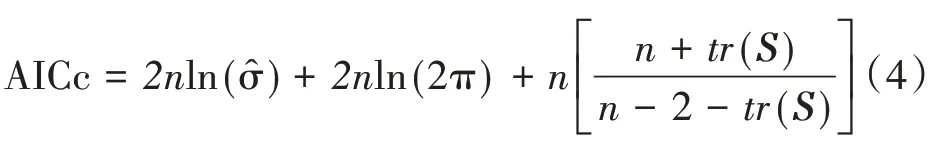
（2）選取空間權函數。空間權重函數的選擇將決定空間權重矩陣的大小，自適應型權重函數可隨回歸點周圍的樣本點密度作相應的調整，而雙重平方函數可剔除距離回歸點較遠且對回歸點幾乎無影響的樣本點。由于本文研究區域內的樣本數據分布不均勻且可能存在距離遠到可忽略的點，因此選擇自適應型雙重平方函數進行回歸分析[22]。wij(1 ≤j≤n)是空間權重函數[27]，其計算公式如下：

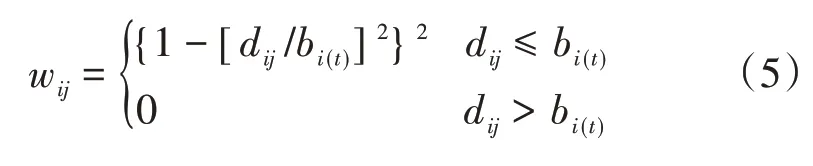
式（5）中：bi(t)為自適應型帶寬，表示樣本點i的t個臨近點的最優帶寬。

（3）計算回歸系數。根據局部加權最小二乘法可得到模型的各回歸系數。參數估計方法計算公式如下：

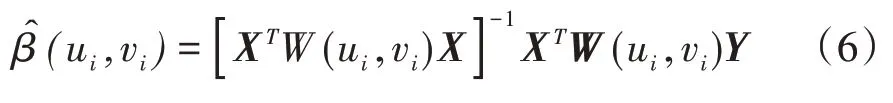
式（6）中：空間權重矩陣是W(ui,vi)一個n × n對角陣,W(ui,vi)=diag(Wi1,Wi2,…,Wij,…,Win)；X,Y分別為自變量與因變量矩陣；為模型參數估計值。

通過地理差異測試對某個特定的變量系數進行異質性檢驗，如果原模型優于比較切換的模型（采用AICc比較準則），則可判斷該變量具有空間異質性。

3 結果與分析

3.1 模型結果及比較

以西安市主城區內的共享單車騎行數據為例，通過建立多元線性回歸模型對建成區環境影響因素進行全局回歸分析。在進行模型分析前，首先對各變量進行多重共線性檢驗與空間自相關性分析。共線性檢驗結果顯示：各影響因素作為因變量時對應的方差膨脹因子均小于5，表明各變量均具有較高的代表性；空間自相關性分析結果顯示：除其他交通樞紐密度X10外，各變量的Moran′s I 和聚集特性值z均為正，且顯著性水平均小于0.05，表明除其他交通樞紐密度因素外，各變量間空間顯著相關且空間分布具有較強的聚集性，因此剔除X10而保留其余變量進行全局回歸分析。全局回歸分析結果如表2～表5 所示。經過多次回歸分析，初步篩選得到研究區域內工作日早晚高峰共享單車出行起訖點分布的顯著影響因素（p＜0.05，顯著水平α=0.05），如表6所示。

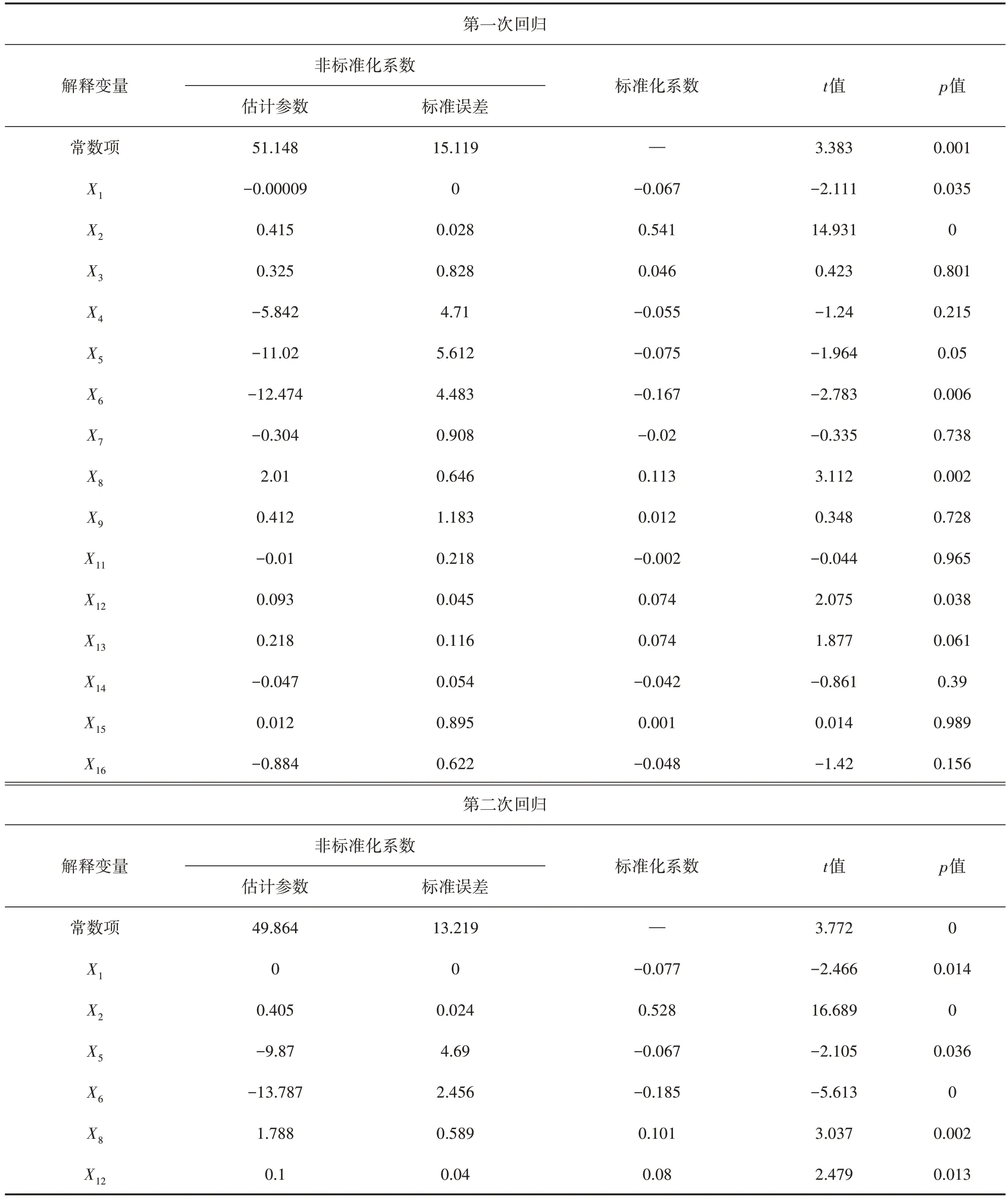
表2 工作日早高峰出行起點分布多元線性回歸分析結果

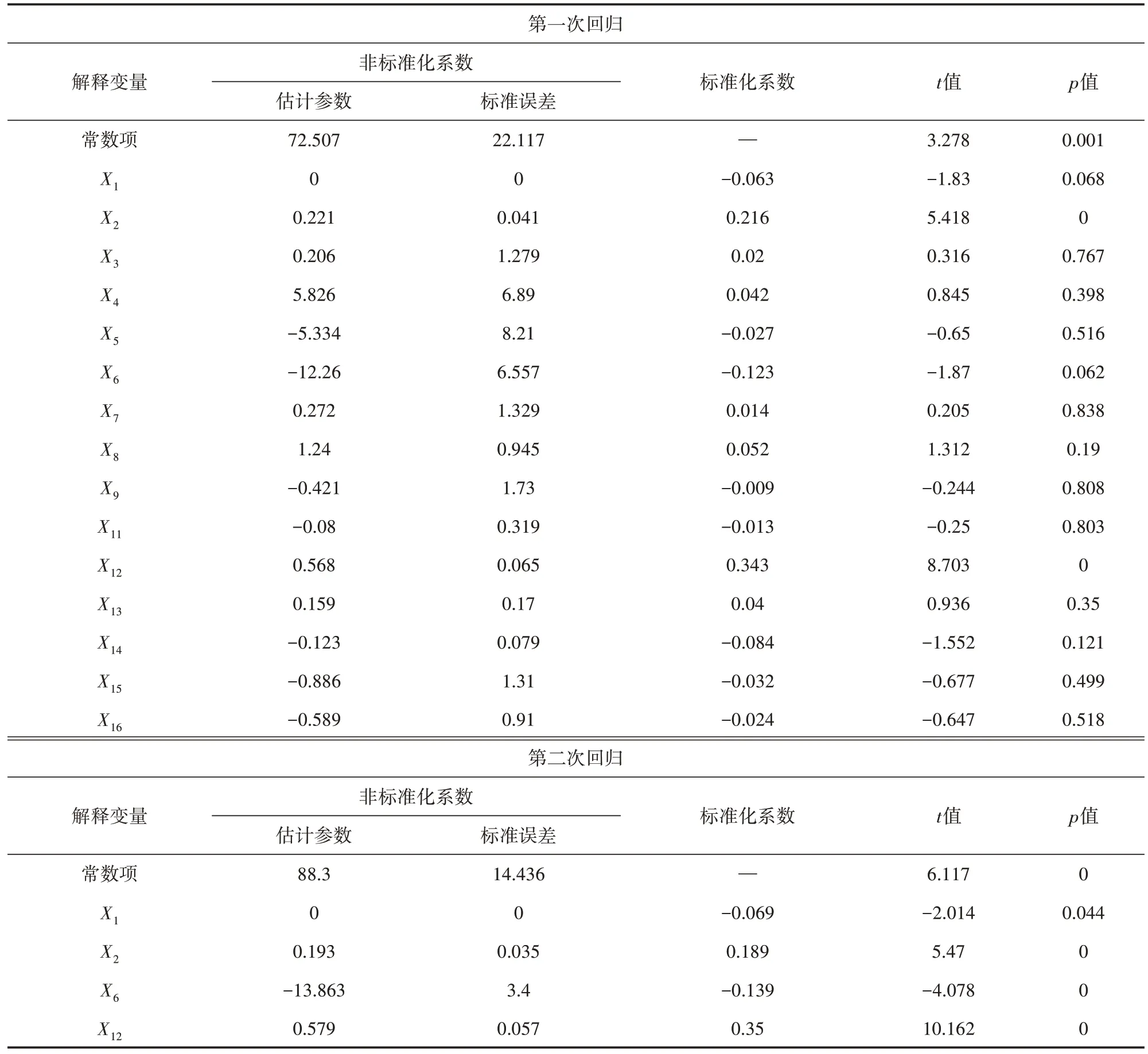
表3 工作日早高峰出行終點分布多元線性回歸分析結果

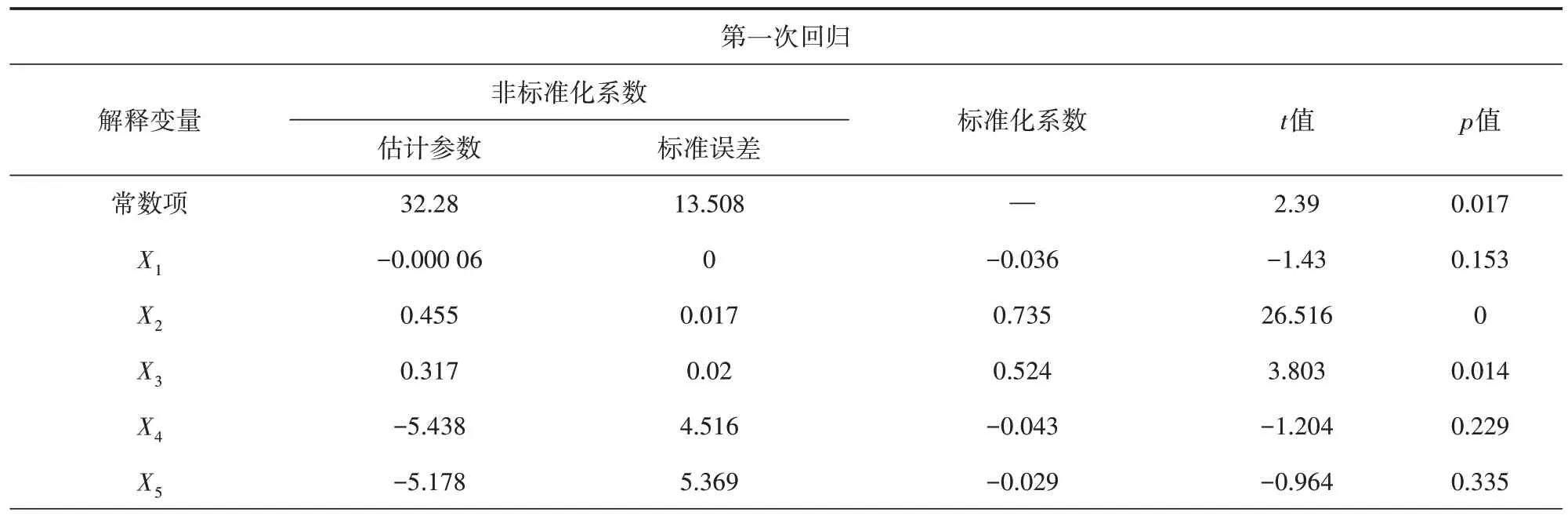
表4 工作日晚高峰出行起點分布多元線性回歸分析結果

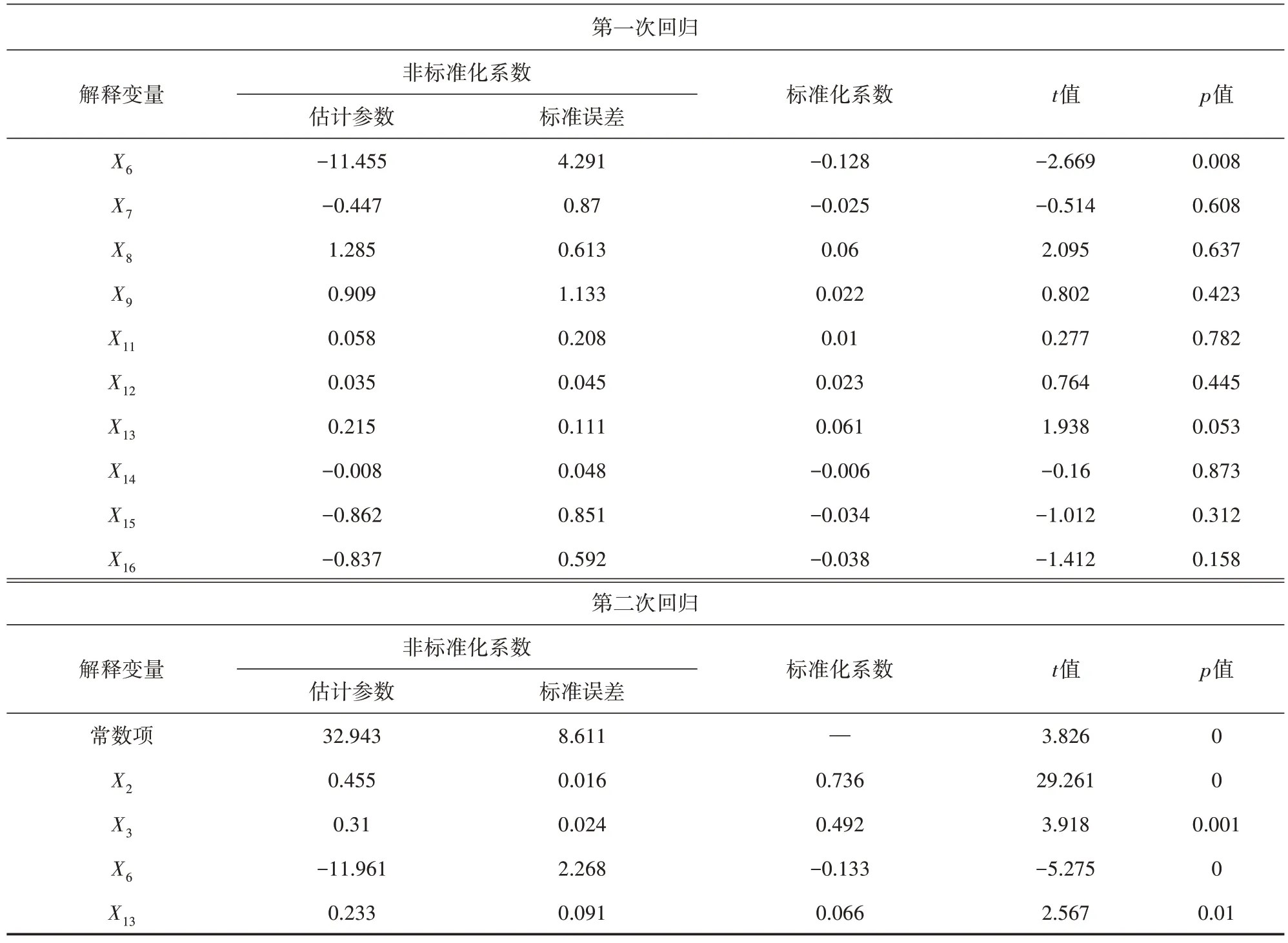
表4 （續）

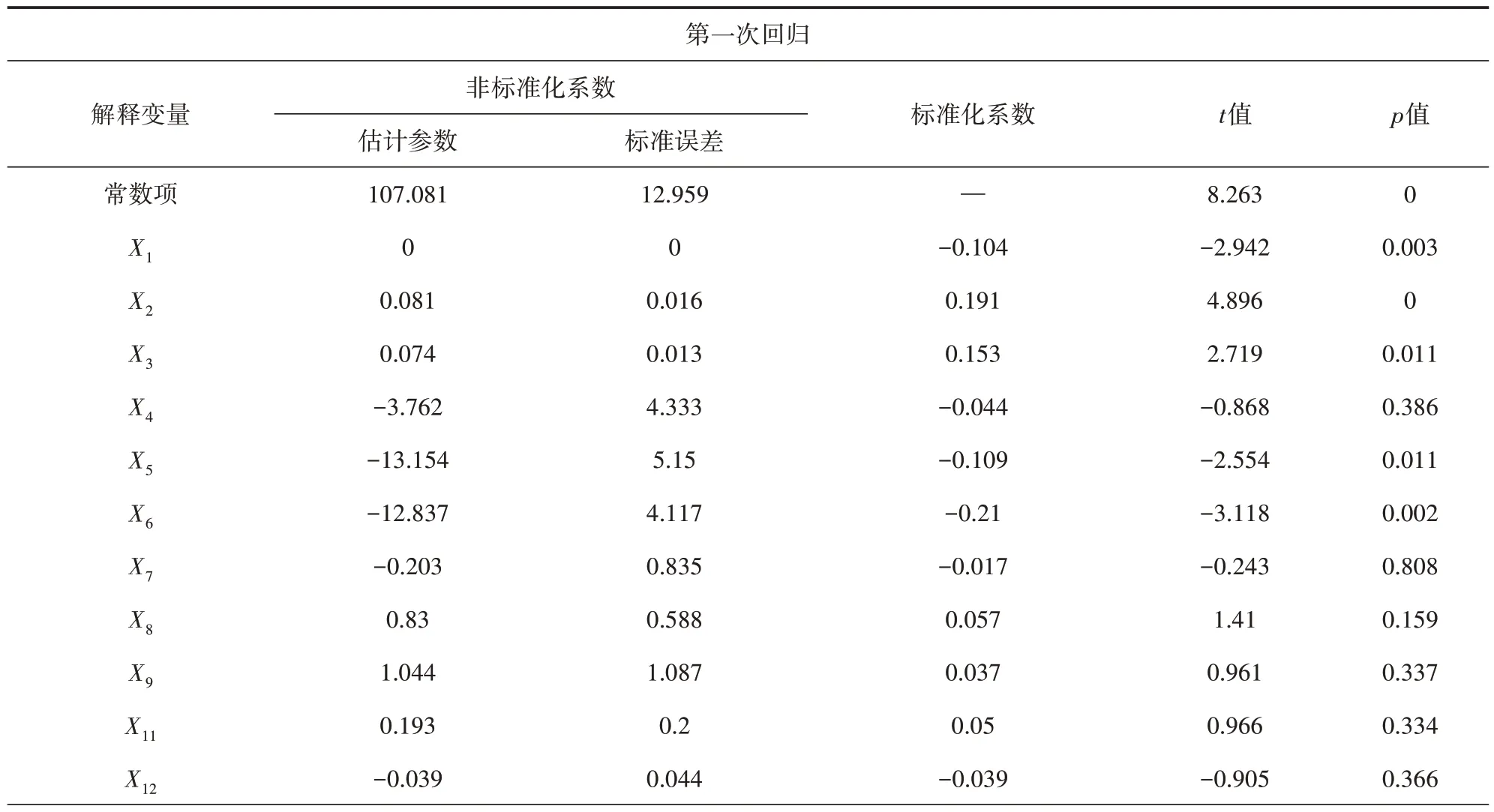
表5 工作日晚高峰出行終點分布多元線性回歸分析結果

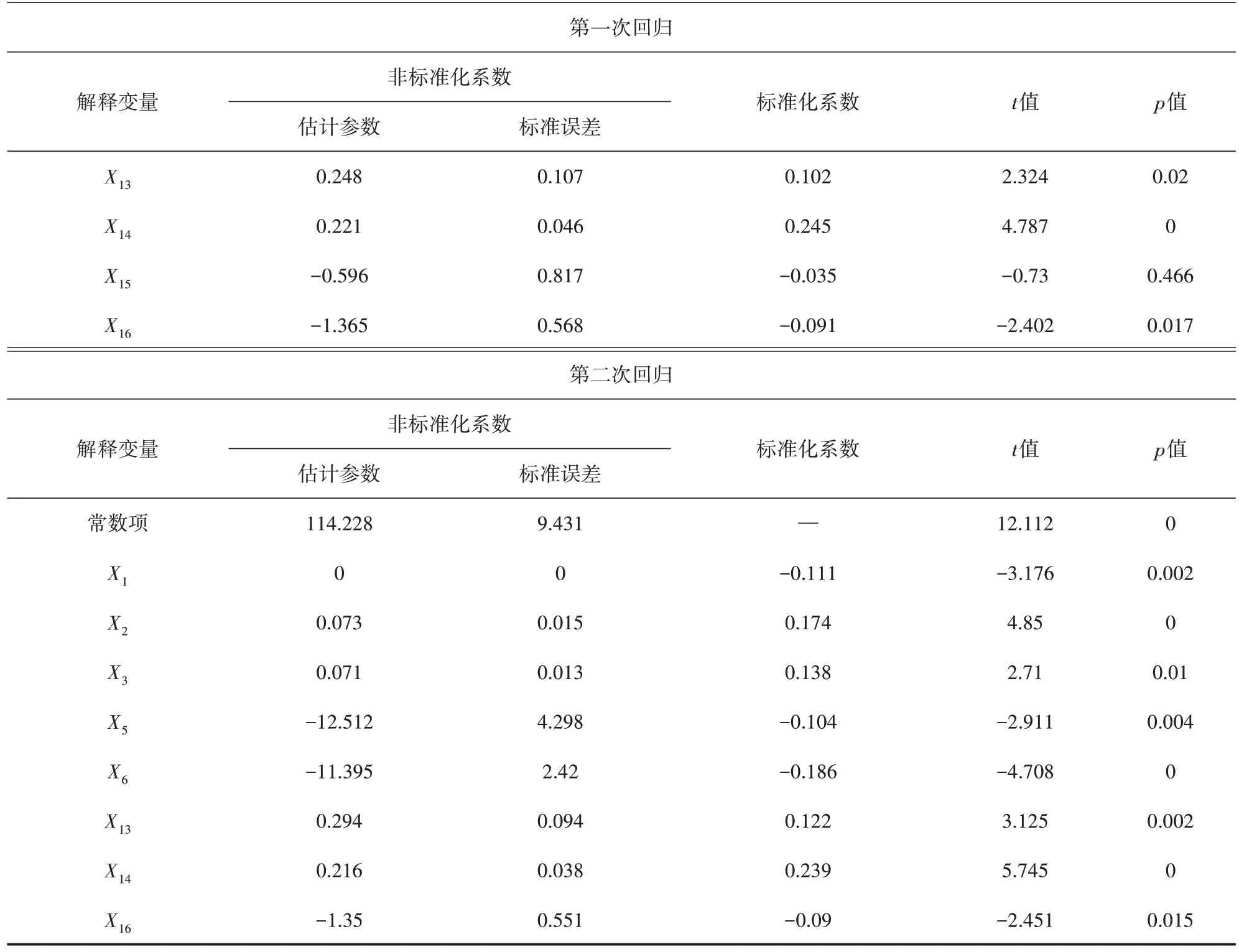
表5 （續）

表6 多元線性回歸模型分析結果

為了確定上述各顯著性影響因子是否具備空間異質性，需構建GWR 模型以得到模型的參數估計值（見表7～表8）。表7～表8中各統計量表示自變量對工作日早晚高峰共享單車出行起終點分布的影響程度。其中，模型參數估計為正值時，表示該解釋變量與因變量正相關；模型參數估計值為負值則相反，且隨著參數絕對值的增大，影響越大[28]。

GWR 模型擬合參數分析結果如表9 所示，分析得到在不同時段對共享單車起終點分布的影響具有較為顯著的空間非平穩性的因素，即這些因素的空間關系可能是不穩定的。

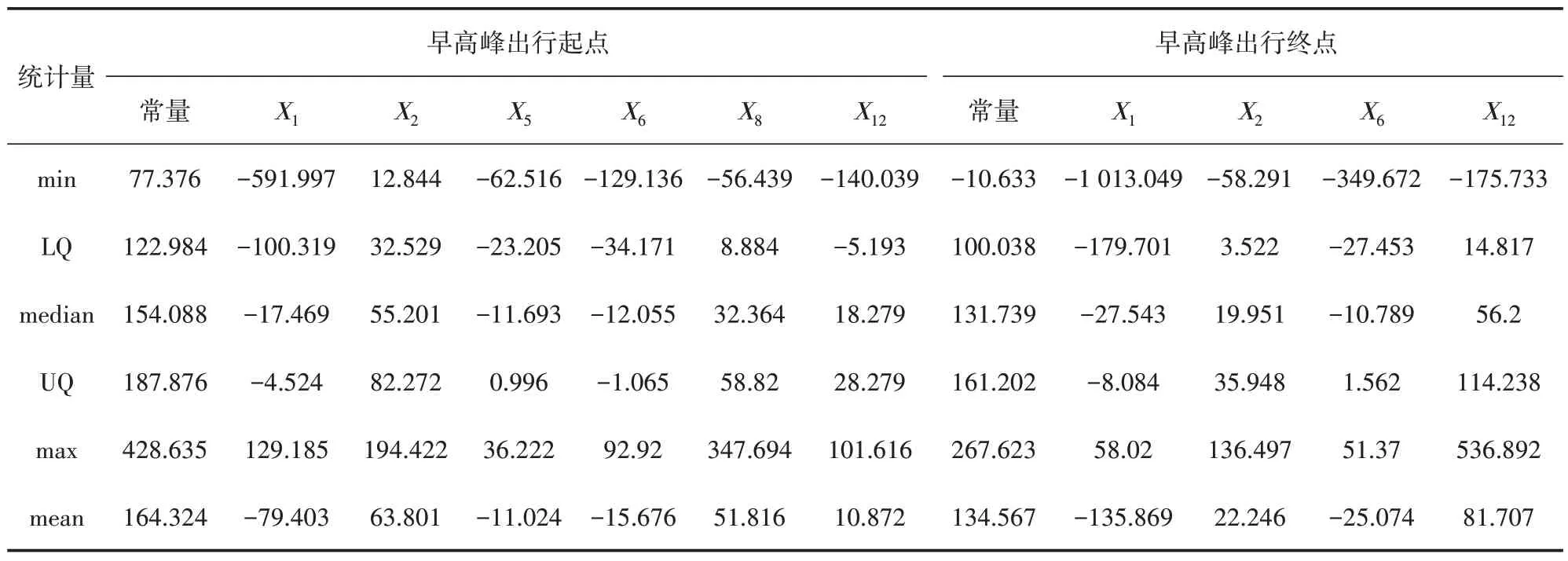
表7 早高峰時段GWR 模型參數估計統計表

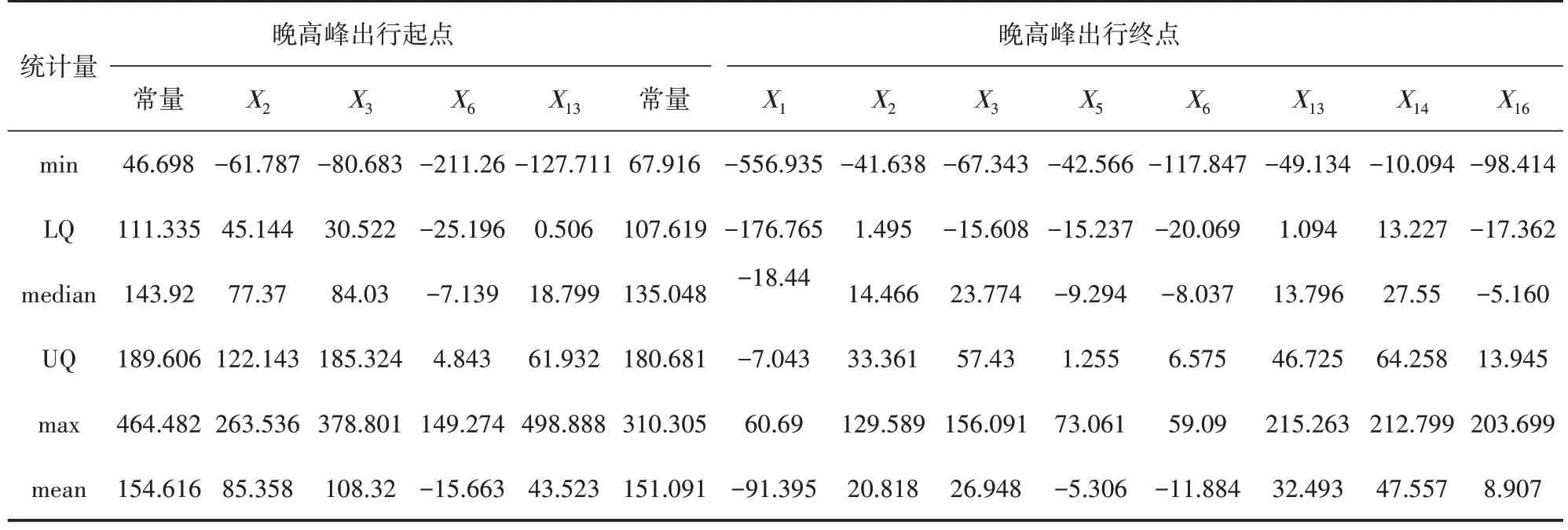
表8 晚高峰時段GWR 模型參數估計統計表

表9 GWR模型擬合參數分析結果

同時利用GWR 4.0 軟件中的地理差異測試（Geographical Variability Test）功能對各變量（見表6）系數的異質性進行檢驗。地理差異測試通常用來識別局部與全局性影響因素，該測試通過對兩個GWR 模型（第一個是將某一個變量作為全局變量，將其他所有變量作為局部變量的GWR模型；第二個是將所有變量作為局部變量的GWR模型）的AICc 值進行比較，如果第二個模型的AICc 值小于第一個模型，判斷標準（DIFF of Cri?terion）值小于0，則該變量是因變量的局部影響因素（即具有空間異質性），否則該變量為全局影響因素。本文進行多次回歸分析，剔除不具備空間異質性的影響因素（DIFF of Criterion 為正的因素），最終得到：在對工作日早高峰出行起點、終點與晚高峰出行起點、終點分布影響因素的測試中，DIFF of Criterion 小于0 的影響因素分別為共享單車設施分布密度（-158.186913）、企業密度（-221.139065）、共享單車設施分布密度（-229.317614）、餐飲類密度（-34.104404），即表明在工作日早高峰和晚高峰時段，共享單車設施分布密度對共享單車出行起點的影響均具有空間異質性；企業密度在工作日早高峰時段、餐飲類分布密度在工作日晚高峰時段對單車出行終點分布的影響存在空間異質性。另外，由于單車投放量對單車騎行率影響較大，車輛投放不足的區域難以單純從騎行軌跡數據的挖掘中發現實際的騎行需求特性，導致GWR 模型影響因素的空間異質性不顯著，因此應不斷追蹤單車投放量與GWR模型的時空擬合程度。

在使用兩種模型對各變量進行回歸分析后，為驗證所選用模型的有效性與準確性，本文主要選取了擬合優度R2、調整后的R2、AICc值以及殘差平方和4 個指標來考量模型的有效性，其中R2值與調整后的R2值越高，AICc值與殘差平方和越小，說明模型的精度越高[29]。如表10所示，GWR模型分析結果中的R2和調整后的R2均高于全局回歸模型中的數據；在工作日早、晚高峰時段，GWR模型對單車起終點回歸分析的R2比全局回歸模型分別提高了0.428,0.378,0.208 和0.309；同時，GWR 模型的AICc 值與殘差平方和均小于全局回歸模型。綜上可知，GWR模型在回歸分析中考慮了地理空間要素的影響，具有較強的有效性與準確性，較全局回歸模型更適用于本研究。

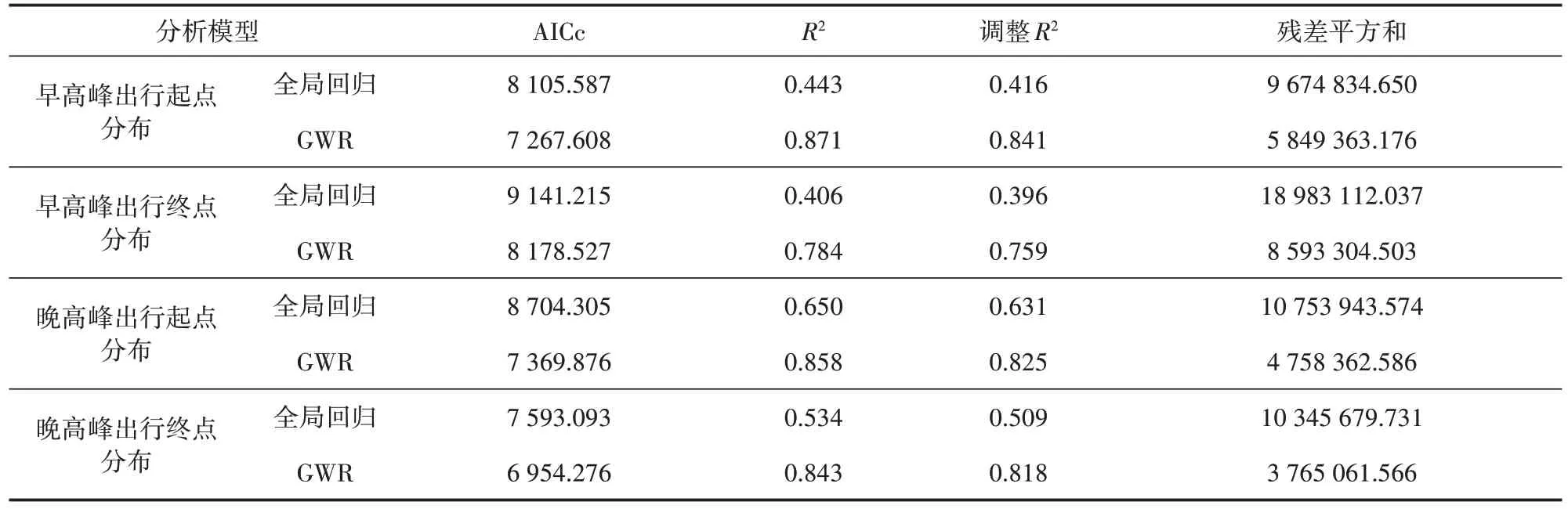
表10 OLS與GWR模型的比較結果

3.2 結果分析

結合3.1 節模型估計結果中具有空間異質性的顯著變量，通過可視化分析工具從早、晚高峰出行起點及早、晚高峰出行終點兩方面對研究區域內共享單車的分布差異及其內在原因進行詳細梳理。

（1）出行起點

模型估計結果表明，在工作日早、晚高峰時段，共享單車設施分布密度對單車出行起點分布的影響具有空間異質性，估計參數空間分布如圖2所示。共享單車設施分布密度因素在西安市南、北部區域對單車的分布表現為較強的促進作用，而在中部及東部地區表現為抑制單車出行。在北部區域，共享單車設施分布密度對單車分布的促進作用在早高峰時段更為明顯。在南部區域，早高峰出行起點的促進區域相對于晚高峰分布更為集中。上述分布差異的原因在于西南區域的學校、企業、商業居多（例如小寨商圈及各大高校的分布），產生了較高的單車使用需求，共享單車設施分布密度便成為促進或抑制單車出行的一個重要指標；而東北角以及中心區域開發尚未成熟（如大明宮、漢長城），共享單車的投放量較低，因此對單車的使用產生較強的抑制作用。

（2）出行終點

企業密度與餐飲類分布密度估計參數空間分布如圖3 所示。從中可看出，在西部區域，企業密度對早高峰單車出行終點的分布具有明顯的促進作用，這與該區域內較為密集的企業分布、公共交通覆蓋不足（相對稀疏的公交線網與軌道交通站點）等原因密不可分；中部及東北區域的企業密度對早高峰共享單車出行終點的分布具有顯著抑制性，可能與該區域內企業分布較少有關，公交、地鐵和私家車成為主要出行方式。

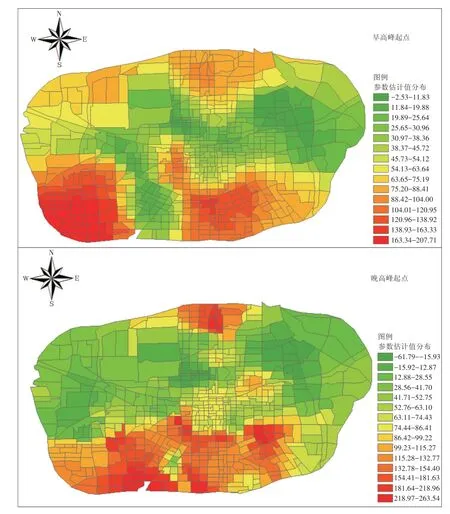
圖2 共享單車設施分布密度估計參數空間分布

另外，在晚高峰時段，中心區域的餐飲類分布密度相對于外圍區域對共享單車出行終點的影響表現出更強的抑制性。這是由于中心區域較為發達，餐飲分布較密集，公共交通等設施發展較為完善，為用戶出行提供了較多的出行方式選擇，因此餐飲類分布密度對單車出行的吸引相對較弱；而外圍區域分布有較多的工業、科技園區且餐飲類分布較為分散，從而產生大量以就餐為目的的騎行需求。

4 結語

本文從城市建成區環境因素出發，綜合確定影響共享單車出行分布的4 類因素，通過構建多元線性回歸模型對各指標進行全局回歸分析，剔除無關變量，得到影響共享單車出行起訖點分布特征的顯著性指標，根據模型分析結果可判斷出各指標對因變量的作用程度及方向（正相關或負相關），有利于決策者了解單車騎行環境的優劣狀態。

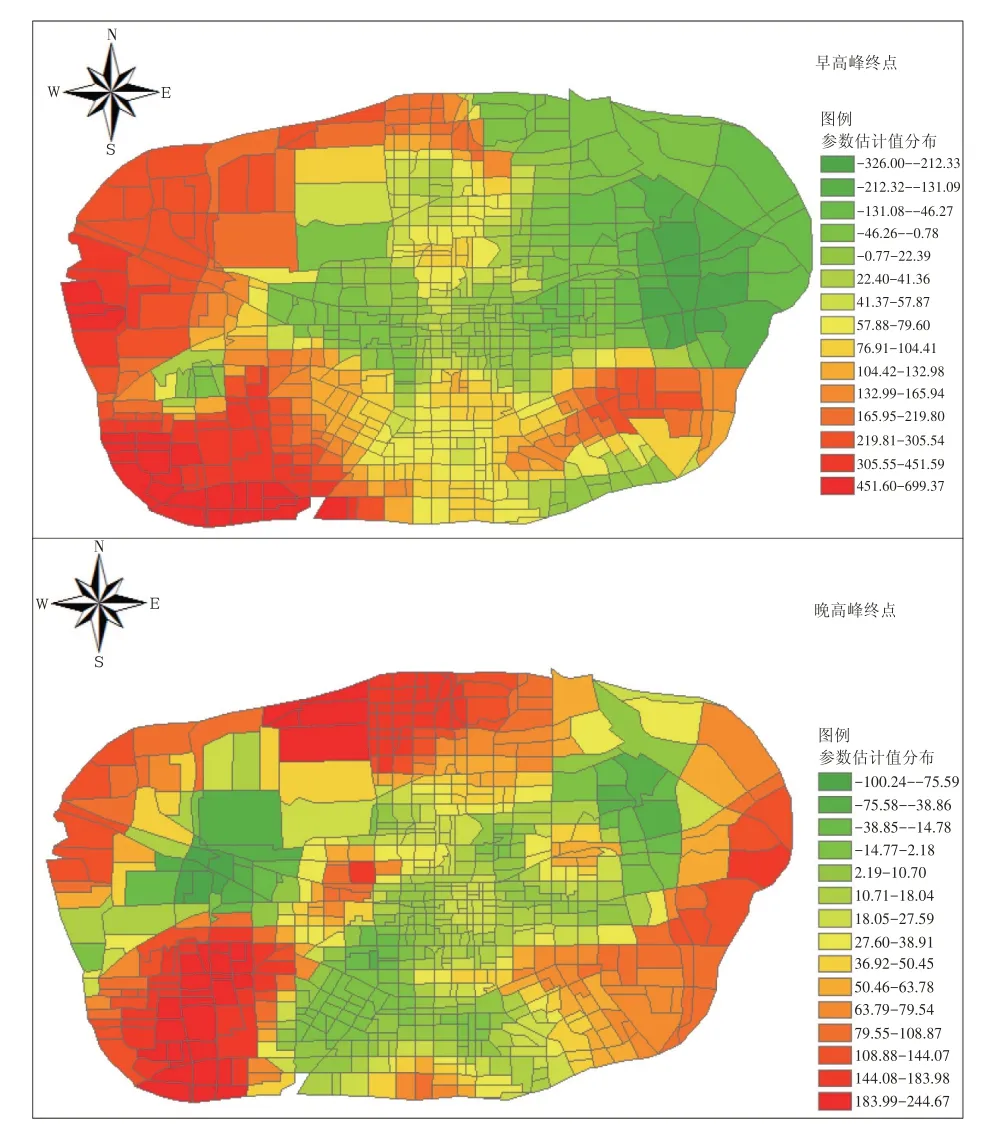
圖3 企業密度與餐飲類密度估計參數空間分布

通過構建地理加權回歸模型，根據模型的參數估計結果，可判斷各影響指標所具有的空間非平穩性，并利用地理差異測試，剔除全局性影響因素，得出工作日各時間段（早、晚高峰）內共享單車出行起訖點分布的空間異質性因素，可為如何進行資源配置以更好地滿足不斷變化的用戶需求提供參考。

通過對西安市主城區的共享單車出行數據進行模型擬合可知：在工作日早高峰和晚高峰時段，共享單車設施的分布密度對單車出行起點分布的影響具有空間異質性，而企業密度在工作日早高峰時段、餐飲類分布密度在工作日晚高峰時段對共享單車出行終點分布的影響存在空間異質性。對這些因素進行可視化分析，決策者可直觀地看出不同時空下影響單車出行OD 的關鍵因素，以選取合適的改善方案來提高用車率。

在后續的研究中，可將個體屬性等因素納入研究范疇，以提高變量的解釋能力，為管理者提供更科學合理的決策支撐依據，為共享單車的投放和調度提供更具針對性的指導。