考慮滑輪直徑的繩系并聯機器人精度分析

冀洋鋒，林 麒，彭苗嬌，吳惠松

(1.集美大學誠毅學院機械工程系,福建 廈門 361021；2.廈門大學航空航天學院,福建 廈門 361005；3.集美大學輪機工程學院，福建 廈門 361021)

0 引言

新型飛行器在研發過程中需要在風洞中進行吹風試驗，而吹風試驗也是空氣動力學研究中比較常用的方法[1]。在風洞試驗中，為了模擬飛機真實的飛行過程，通常需要把飛行器的縮比模型使用一定的方式進行固定，并且還能夠根據不同的試驗項目改變模型的位置和姿態，以此評判飛行器設計的各種狀況。因此，設計合適的支撐方式是風洞試驗的一項關鍵技術。傳統的硬式支撐包括尾撐式、背撐式和腹撐式等，硬式支撐一個無法避免的問題是支撐桿對流場的干擾，且這種干擾會逆流上傳，即使后期通過專門的試驗來修正也無法完全消除流場干擾對測試結果的影響[2]。

繩系并聯機器人(cable-driven parallel robot,CDPR)是一種比較新的支撐方式，采用彈性模量比較高而直徑比較細的彈性繩索代替原來的硬式支撐桿，動平臺的位姿改變依靠改變柔性繩索長度來實現。與傳統的硬式支撐方式相比，該種支撐方式具有一系列優點，例如具有較大的工作空間[3-5];更高的承載能力和更好的能量利用效率[6-7];較低的建造成本[8-9];部件簡單且方便拆卸和重新組裝;具有較高的安全性[10]。尤其是同一套支撐機構可以完成多種靜、動態試驗項目，這一點對于節省試驗成本以及提高新型飛行器的研發效率具有重要的意義[11]。

典型的風洞試驗模型繩系并聯機器人支撐系統是法國國家航天航空研究中心支持的SACSO項目。該機構研究的9 繩牽引系統SACSO-9目前已通過了風洞自由飛試驗的可行性模擬分析，并進一步將其用在了飛行器初期概念設計中的立式風洞的尾旋試驗[12-13]。Lambert等[14-15]將一套8繩牽引的并聯機構安裝于風洞中進行了吹風試驗，研究了鈍體模型流動控制情況。文獻[16]針對大尺寸模型構建了一套“柔性懸掛系統”，該支撐方案利用尾撐以及前后四根鋼索吊起機身進行吹風試驗，在LENSⅡ激波風洞中，該系統用于支撐X-51全尺寸模型，進行了氣動熱和推進研究。文獻[17]根據不同的風洞試驗的特點，采用了不同的繩系支撐方式。文獻[18]對應用于風洞試驗的繩系并聯支撐機構進行了一系列探索。文獻[19-20]對繩系并聯機器人進行了不同程度的研究工作。文獻[21]研制了一套張線支撐系統，并于3.2 m亞聲速風洞進行了大迎角試驗。文獻[22]設計了一套軸承與張線組合的支撐系統，用于低速風洞的彈體模型的虛擬飛行試驗。文獻[23]開發了一套張線支撐系統，并進行了一系列實驗工作。

在低速風洞試驗過程中，模型姿態角的誤差是試驗數據誤差的主要來源之一，為了提高試驗數據的精度，必須在可行的情況下盡可能提高模型姿態角的精度。相比硬式支撐，繩系并聯機器人支撐機構中采用的柔性繩索只可以單方面承受拉力，動平臺姿態改變及控制很大程度上取決于繩索長度的精確計算。而滑輪的存在，會影響繩索長度的計算精度，進而影響動平臺的位置精度。以往繩系并聯支撐機構的研究中，只有極少數對動平臺的位置精度進行了初步研究。本文對繩系并聯支撐機構的精度影響因素進行深入分析，以期提高應用繩系并聯機器人支撐模型所得風洞試驗測試數據的準確性和有效性。

1 樣機建立

采用8根繩索牽引的實驗樣機CDPR-8(cable-driven parallel robot with eight cables)如圖1所示。在該類機構中，繩索一端與模型相固定，另一端經過滑輪后與電機滑塊相固定。滑塊在電機驅動下做直線運動，可以通過改變各牽引繩索的長度，從而調節繩索預緊力，以改變模型的位置和姿態。

為了描述及后期分析，建立如圖2所示的靜坐標系和動坐標系。其中，靜坐標系原點位于機架正下方中心，動坐標系原點位于模型幾何形心處。由于滑輪的機架位置是固定的，因此動平臺的工作空間由滑輪與模型之間的繩索長度決定，即由模型上連接點的空間位置決定。圖2中，滑輪中心點位置Di(i=1,2,…,8)及模型上繩索連接點的坐標Pi(i=1,2,…,8)在樣機中的初步取值詳細情況見表1。其中：Di為滑輪在靜坐標系中的位置；Pi為繩索連接點在動坐標系中的位置。

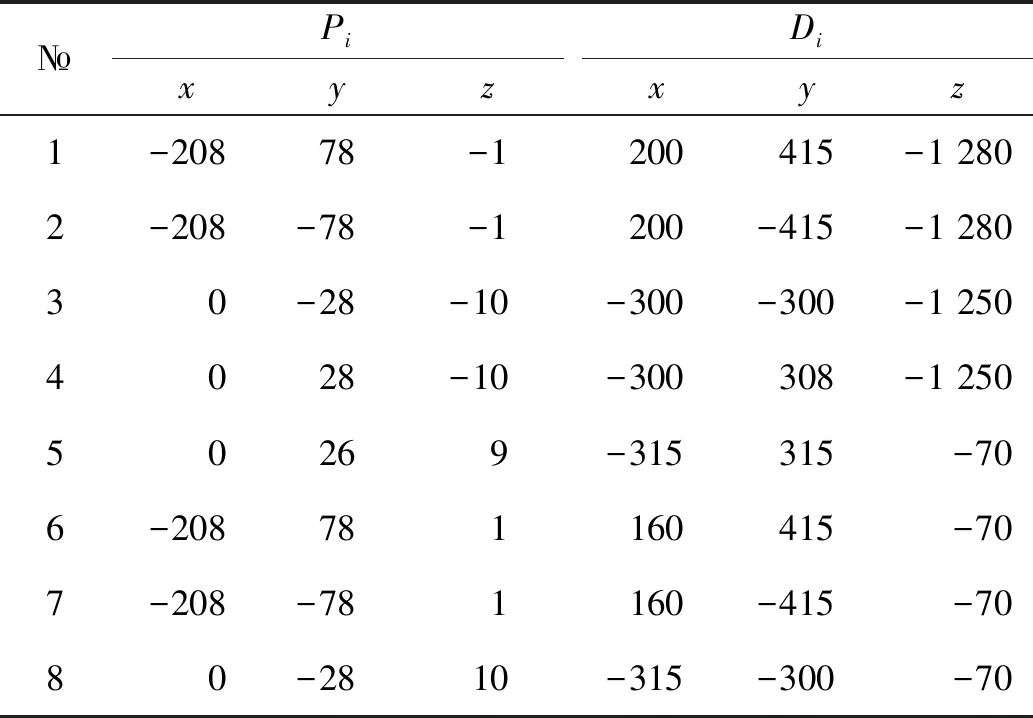
表1 CDPR-8各牽引點參數Tab.1 Parameters of attaching point in CDPR-8

2 機器人的幾何關系建立

在繩系并聯機器人支撐機構中，模型姿態與繩索長度有關，因此需要建立機構的幾何關系模型，以方便對牽引繩長與模型位置姿態之間的關系進行量化分析和精確計算。

2.1 CDPR-8的幾何關系模型

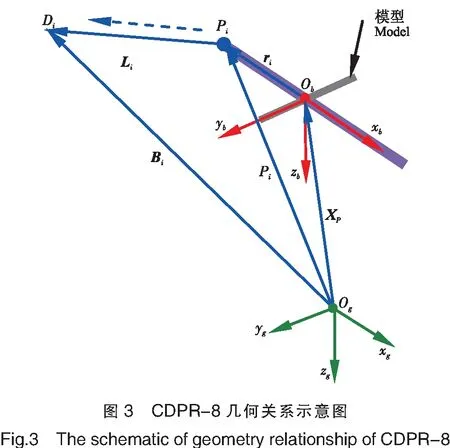
圖3是CDPR-8的機構幾何關系示意圖。其中：粗線十字架代表飛機模型，長軸表示機身主軸，短橫軸代表模型的翼展方向；Bi表示驅動點(滑輪中心)在靜坐標系中的位置；ri是一個常數矢量，表示在動坐標系中模型上的連接點；XP表示模型的參考點在該坐標系中的位置；Li表示繩索長度的矢量，在靜坐標系中，可以通過式(1)獲得，

Li=Bi-XP-Rri

(1)

其中：R是從動坐標系變換到靜坐標系的雅克比矩陣。

在依靠繩索驅動的并聯機器人中，動平臺的姿態和位置是通過繩長來控制的，因此代表繩索長度的矢量Li是系統位姿能否精確控制的關鍵。在設計模型運動的控制率時為了方便分析，通常把機架上的滑輪簡化成理想的鉸點，即繩長由機架的滑輪中心點Di和動平臺上的連接點Pi決定。

然而，實際機構中滑輪都具有一定直徑，因此繩索無法穿過滑輪軸心，況且繩索與滑輪接觸點并非理想的固定點，而是隨動平臺(飛行器模型)姿態改變而隨時發生變化的，采用上面的理想簡化算法必定會對以繩長及其變化量進行模型姿態和運動控制的機構精度帶來誤差。為了給模型位姿的精確控制提供準確的參考數據，需要分析滑輪簡化前后對繩索長度的影響，以此來計算對樣機精度的影響。為此建立包含滑輪直徑的機構幾何關系式，以方便對這一影響情況進行量化分析。

2.2 包含滑輪形狀的CDPR-8幾何關系

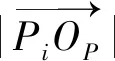
(2)

3 滑輪直徑影響量化分析

3.1 繩索絕對長度與相對長度的影響

理論上來說選取任何一根繩索長度都不影響分析的最終結論，不失一般性，這里選取第7組數據，即7號滑輪點和連接點的數據進行計算分析。根據樣機的相關幾何參數，動坐標系原點在靜坐標系中的位置即圖3中矢量XP的值,XP=(0,0,-582)，滑輪直徑為10 mm，以下分析皆在此工況下進行。相關數據代入式(1)和式(2)中，可以得到不同迎角θ下實際繩長L、理論繩長L0、絕對誤差ΔL(ΔL=L0-L)以及相對誤差δ(δ=ΔL/L0)，計算結果如表2所示。

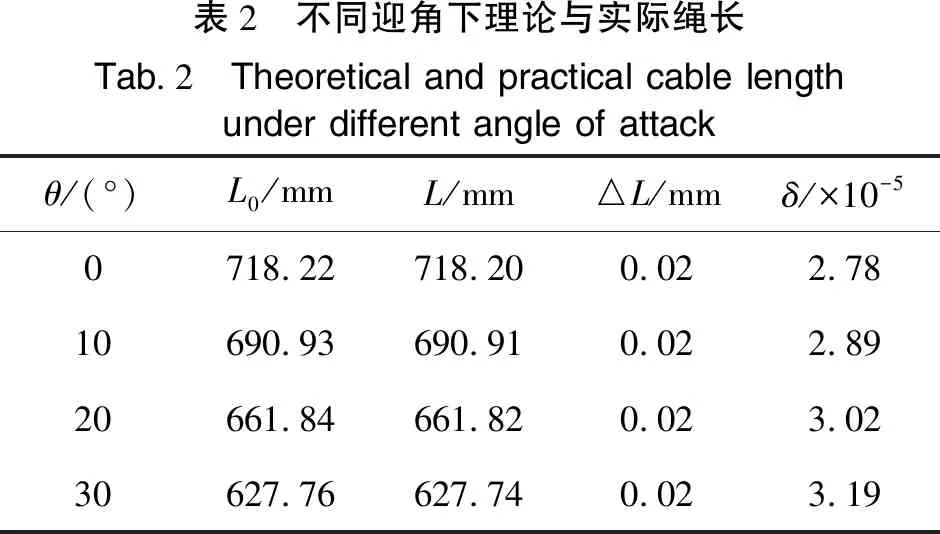
表2 不同迎角下理論與實際繩長Tab.2 Theoretical and practical cable lengthunder different angle of attackθ/(°)L0/mmL/mm△L/mmδ/×10-50718.22718.200.022.7810690.93690.910.022.8920661.84661.820.023.0230627.76627.740.023.19

由表2可知，實際值與理論值的絕對誤差△L在微米級，而相對誤差δ在10-5級左右，這樣的結果表示一根繩索長度的變化對系統影響不大。然而在CDPR-8中，模型是通過8根繩索來牽引的，因此有必要分析不同的迎角下8根繩索采用理論值代替實際值時的誤差情況。

圖5表示迎角在一定范圍內變化時，所有繩索的ΔL值隨不同的迎角的改變情況。從圖5中可以看出，迎角從0°到30°變化過程中，ΔL保持在大約10-5m，這一情況與單獨一根繩索的比較接近。這是因為在實際的樣機中，繩長比滑輪半徑的值大得多，而且8根繩索的長度彼此之間差別不大，都處于同一量級，因此圖4所示矢量三角形內兩個長邊的長度非常接近。圖6為不同的迎角下8根牽引繩索的相對誤差隨迎角變化情況，由于8根牽引繩初始長度比較接近，所以圖6中結果與圖5走勢比較類似。

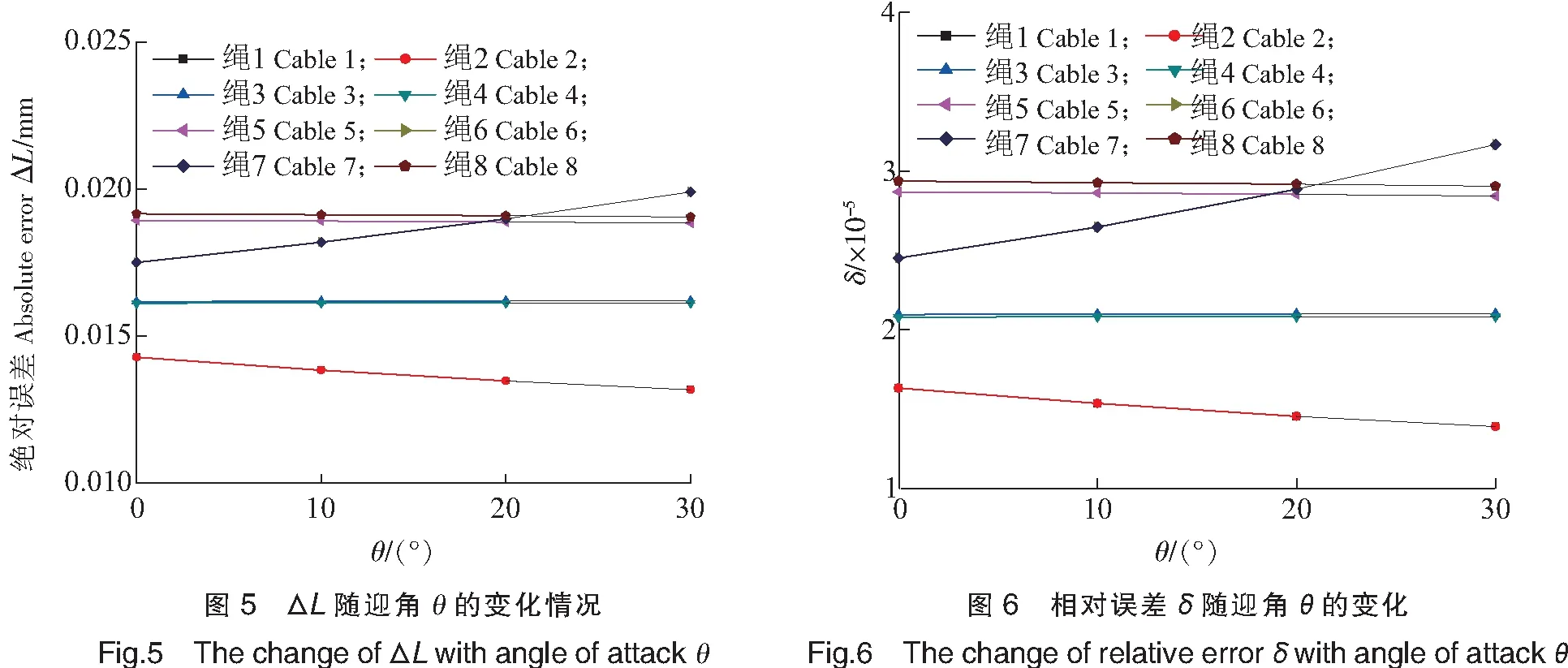
3.2 模型位置和姿態的影響

將圖5中計算結果結合理論繩長，按照文獻[24]中的方法進行機器人正解求解，可以得到圖7的結果。其中，X、Y、Z分別表示模型沿三個坐標軸方向的位置改變；而f、α、β分別表示模型繞這三個坐標軸旋轉產生的角度變化。圖7中對模型位姿的影響誤差為10-5m，對姿態角的影響為10-3(°)，可見在本樣機參數下，用繩索的理論長度替代實際長度對模型的位置和姿態所產生的誤差是高階小量，其影響基本可以忽略不計。

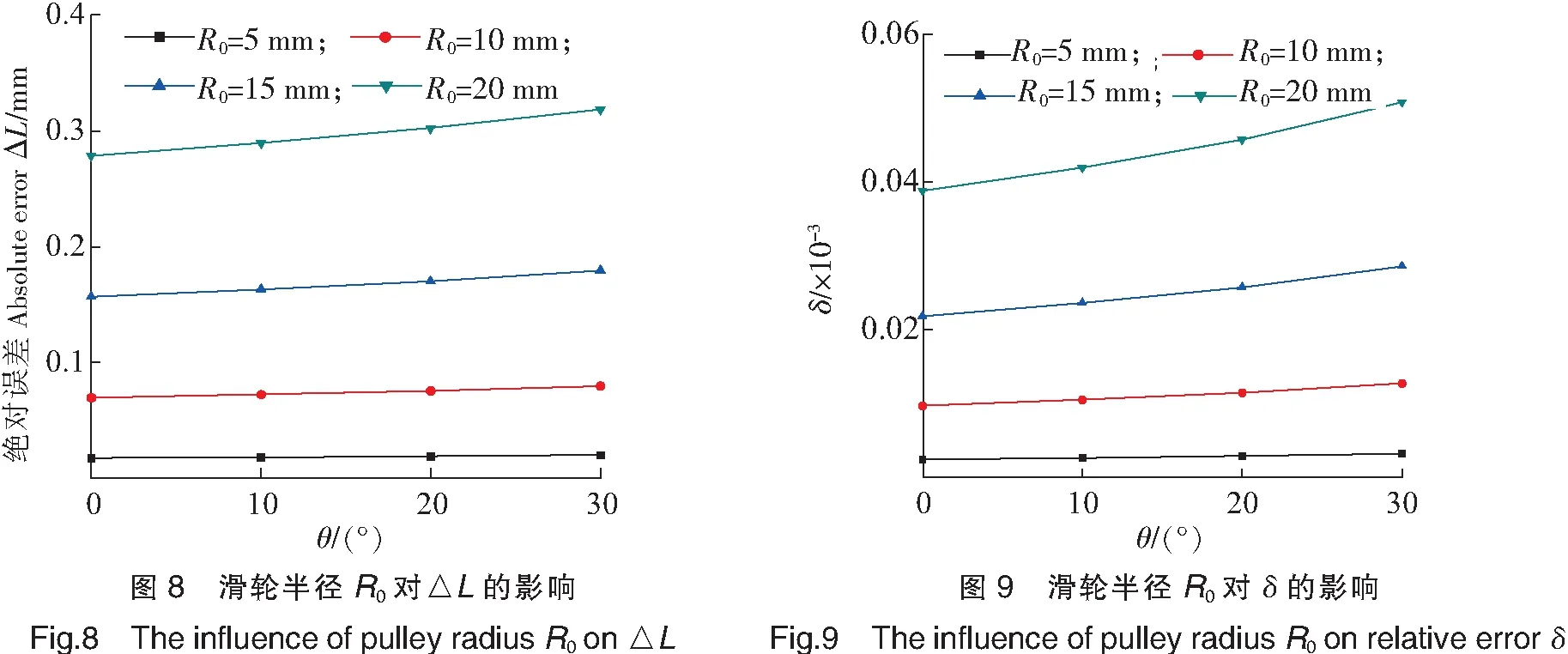
以上結論為假定滑輪直徑為10 mm時得到的，當滑輪直徑發生變化時，情況會有所不同。為此，考慮滑輪直徑分別為20 mm、30 mm、40 mm的情況，計算不同迎角下實際繩長，并與理論繩長進行比較，結合表2中計算結果，可以得到不同直徑下絕對誤差△L和相對誤差δ，結果如圖8和圖9所示。圖8為不同滑輪半徑時△L隨迎角變化情況，可以看出隨著迎角的增加，同一滑輪半徑下的△L略有增加，但變化并不明顯。不同滑輪半徑R0所對應的△L變動明顯，這說明滑輪半徑是影響繩索長度的決定性因素。

同圖8中結果類似，圖9中同一滑輪半徑下的相對誤差δ隨迎角變大略有增加，不同滑輪半徑所對應的相對誤差更為明顯，尤其是當滑輪半徑R0=20 mm，迎角30°時，δ超過了0.005%，此時若使用理論繩長值代替實際值，將對機構的姿態精度帶來明顯的誤差，這顯然是不可取的。

3.3 滑輪選用的通用性原則

以上分析表明，當機構及繩索長度大體確定以后，滑輪半徑R0對繩長的計算程度有關鍵性的影響。參考圖4中各矢量之間的關系，實際繩長L、理論繩長L0、相對誤差δ以及滑輪半徑R0之間的關系由式(3)決定：

(3)

其中，理論繩長L0取表2中的值718.22 mm，根據式(3)，可以計算得到L/R0與對相對誤差δ的變化規律，如圖10所示。圖10中曲線的走勢近似一條雙曲線，表明L/R0和δ呈現反向變動關系，即當繩索長度確定以后，半徑R0越小，則L/R0越大，相對誤差δ就越小。由此可以得出一個重要結論：當支撐機構模型大小及繩長近似確定以后，選用直徑較小的滑輪可以提高繩索長度的精度，從而提高繩系并聯機器人機構的位置和姿態精度。這一結論同樣適用于此類樣機系統的結構設計。

4 結論

本文搭建了一套應用于低速風洞試驗模型支撐系統的繩系并聯機器人樣機，建立了包含滑輪直徑的樣機幾何模型，分析了滑輪直徑對繩索長度誤差的影響情況。經過詳細的計算和分析，得出了以下結論：1)在繩系并聯機器人機構中，將滑輪簡化為理想的點對繩索的實際長度具有一定的影響；2)繩長遠大于滑輪直徑時，將滑輪簡化為理想的點所產生的繩索長度相對誤差是一個高階小量，此時可以簡化為用繩長理論值替代實際值，具有一定的合理性；3)樣機的結構和繩索長度大致確定以后，在保證系統安全和強度的前提下，應當盡可能選用直徑比較小的滑輪，這樣可以提高繩索長度求解的精度，進而提高模型位置和姿態控制的精度。